降雨诱发边坡破坏的数值模拟

袁文辉

(南昌市城市防洪事务中心,南昌 330006)

1 概 述

暴雨引起的边坡破坏是重要的岩土工程问题,负孔隙水压力(基质吸力)在暴雨诱发的边坡失稳中起着重要作用。其中,导致边坡破坏的机制是雨水开始渗入非饱和土壤时,引起负孔隙水压力的损失。为此,可以采取非饱和土壤的边坡稳定性分析。同时,为了更好地理解土壤中水的密度与水相能量状态之间的关系,还需要绘制土壤-水特征曲线(SWCC)。模拟非饱和土壤中的水分入渗,除了SWCC参数外,降雨情景(即降雨强度和持续时间)、土壤渗透性和土壤中的初始条件也是非饱和边坡中降雨入渗数值模拟所需的参数。

目前,许多学者针对这些参数的影响进行了相关研究。王花蕊[1]利用灰色系统理论,探究了降雨强度、内摩擦角、内聚力对边坡稳定性的影响。陈乔等[2]利用降雨型滑坡监测模型,对降雨强度、孔隙水压力、含水率对边坡坡失稳破坏成因进行了分析。刘平军[3]分析了边坡稳定性系数与降雨强度的关系,并推导了边坡稳定性公式。刘亚龙[4]通过研究发现,浅层边坡滑动主要出现在强降雨和暴雨中后期,且边坡稳定性与降雨方式、强度、土体入渗能力有关。

本文利用模型的几何、水力和岩土性质作为数值模拟的输入参数,通过参数研究土壤渗透性、SWCC和黏聚力对边坡稳定性的影响。结果表明,不同的降雨强度会产生不同的边坡破坏模式,渗透性和SWCC在非饱和土壤的地面入渗行为中起着重要作用,土壤黏聚力也是非饱和边坡安全的一个重要控制因素。

2 数值模拟分析

2.1 构建模型

选取水库上游典型边坡截面,目标斜坡高度30m,坡度3.3∶1。研究边坡的代表性截面见图1。

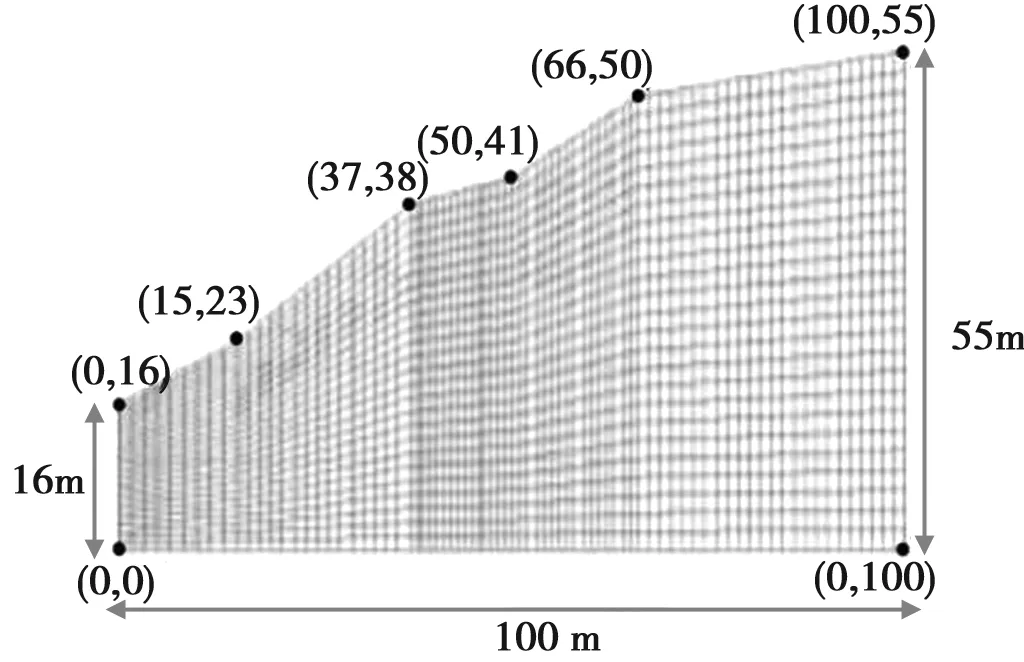
图1 研究边坡的代表性截面

研究参数为渗透性、降雨强度和持续时间、土壤饱和度和黏聚力。为了更准确地预测降雨期间的浅层边坡破坏,应考虑选择内聚值作为非饱和边坡的初始属性。

根据统一的土壤分类系统,该区域的风化花岗岩土壤可归类为SM,沿坡面分布,深度在2～10m之间,假定该边坡为风化花岗岩土层的均质边坡。该区域土壤的物理力学性质和SWCC参数见表1。

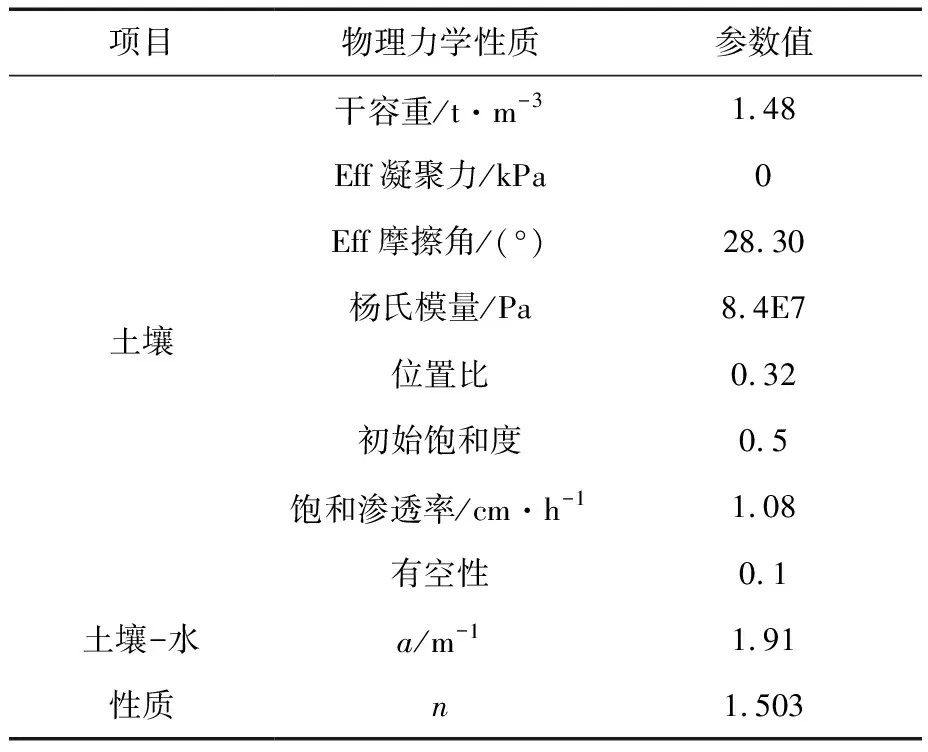
表1 土壤物理力学性质和土壤水分性质

本研究包括渗透分析和边坡稳定性分析,可与FLAC2D-两相流配置同时进行模拟。Van Genuchten方程式(1980)用于研究不同降雨条件下雨水对边坡土壤性质的影响;非饱和土的抗剪强度折减法用于估算雨水渗入土壤的量对边坡安全系数(FOS)的影响。

2.2 水流过非饱和土壤

在FLAC中,Van Genuchten(1980)基于毛细管模型建立一组封闭式方程,用于表示非饱和土壤的水力特性。为了实现由于不同的坡度角,雨水沿坡面渗入土壤的量的可变性,编辑FLAC中提供的调整流量FISH。非饱和土壤的水力特性公式如下:

(1)

(2)

式中:Se为有效饱和度;Sw为饱和度;Sr为剩余饱和度;n、m为曲线拟合系数,m=1-1/n,n>1;Ks、Kr为饱和相对渗透率。

2.3 非饱和土的抗剪强度折减方法

使用Bishop有效应力(1959),稳定性分析中采用的非饱和土的抗剪强度方程如下:

τmax=(σ-ua)tanφ′+χ(ua-uw)tanφ′+c

(3)

或者弗雷德隆德和拉哈德乔(1993年)所示:

τmax=(σ-ua)tanφ′+χ(ua-uw)tanφb+c

(4)

这里Vanapalli等(1996年)将χ定义为:

χ=(Sw-Sr)/(100-Sr)

(5)

式中:Sw、Sr、ua、uw、σ分别为饱和度、残余饱和度、气压、水压和总应力。

在利用抗剪强度折减技术计算非饱和边坡的安全系数时,采用折减后的抗剪强度参数Ctrial和φtrial进行一系列模拟,试验定义如下:

(6)

(7)

式中:Ftrial为试验的安全系数,开始剪切强度降低Ftrial设置为足够小,以确保系统稳定;Ftrial逐渐增加,直到发生破坏,FOS是影响其破坏的关键因素之一。

2.4 可变参数

分析中的可变参数包括降雨强度分布、饱和度、渗透系数、SWCC参数和土壤黏聚力。

2.4.1 降雨模式

本研究假设不同的降雨强度。为了估算土壤的渗透能力,使用与土壤渗透性相等的降雨强度,并选择与流域当前最高降雨强度相似的降雨强度11cm/h。沿斜坡降雨110h,预计FOS增量为10h。

2.4.2 饱和渗透系数

使用两种不同的渗透率,研究其对渗透过程和正孔隙水压力随时间的发展影响。在使用的渗透率中,分别为1.08和10.8cm/h。

2.4.3 SWCC参数

SWCC提供了土壤中水的质量/体积与水相能量状态之间的概念性理解。根据SWCC实验,α、n和θr被确定并用作FLAC中非饱和土的输入特性。n值用于计算Van Genuchten方程中的参数,α(m-1)代表参考孔隙压力P0(kPa)。另一个拟合参数是剩余饱和度θr,与孔隙压力计算中使用的有效饱和度有关。将残余含水量定义为土壤水分从主要通过毛细作用保持在土壤中到主要通过吸附力保持在土壤中的含水量。在本研究中,为了估计该参数的影响,使用FOS获得的0和0.11的值。其中,零剩余饱和度是一种特殊情况,因为饱和度等于有效饱和度。

2.4.4 饱和度

为了估计饱和度对边坡失稳阈值随时间的影响,假设不同的饱和度值。这些估计值分别为0.4、0.5和0.6,其中0.5为实验值。

2.4.5 土壤黏聚力

土壤黏聚力被理解为将土壤颗粒固定在一起的力。对于非饱和土,黏聚力是联锁、物理、化学作用产生的有效内聚力以及由颗粒间力或吸力和表面张力控制的表观内聚力的总和。为了通过数值模拟了解所选内聚力对降雨条件下边坡破坏的合理预测影响,假设5个值。假定的黏聚力值为0、5、10、20和30kPa。

3 结果和分析

3.1 渗透性的影响

为了探究降雨20h后孔隙压力随深度的变化,两种不同的渗透性值k1(k1=1.08cm/h)和k2(k2=10.8cm/h)导致土壤在降雨条件下的不同行为。在这种情况下,假设土壤的内聚力和饱和度分别为10kPa和0.5kPa。随着渗透性的增加,更多的水渗入边坡。对于渗透值较高的土壤,正孔隙压力在边坡表面附近显著发展。降雨20h后孔隙压力随深度的变化见图2;雨水渗透对边坡安全系数的影响见图3。

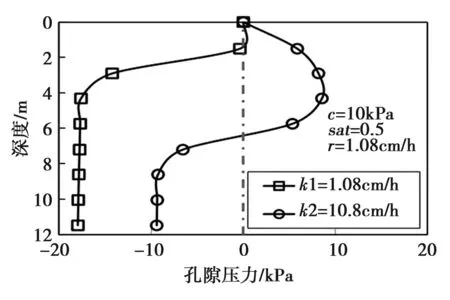
图2 降雨20h后孔隙压力变化

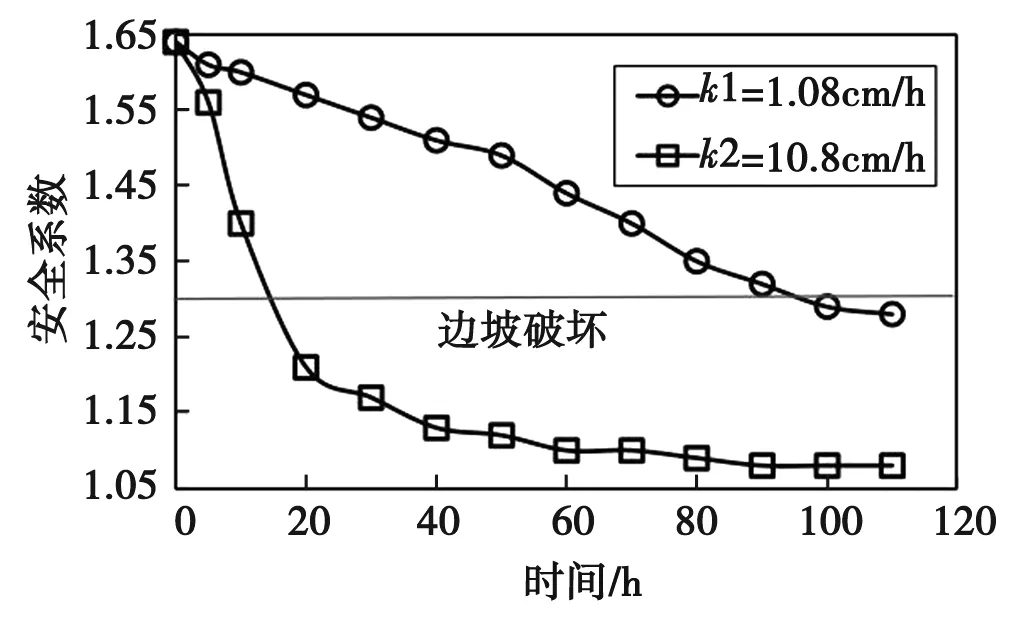
图3 雨水渗透对边坡安全系数的影响

由图2和图3可知,由于渗透率较低,基质吸力显著降低。由图2和图3能够估计给定降雨时间后形成的湿润带,对于降雨为k1的边坡,可以估计约6m的湿润深度。对于低饱和渗透系数,边坡内的负孔隙压力下降得更慢,任何变化只能在地表附近观察到。因此,在渗透率较低的情况下,可以看到FOS的稳步下降。另外,在受降雨影响的高渗透性土壤中,FOS显著下降。

3.2 降雨强度的影响

为了估计降雨强度对边坡FOS的影响,考虑低渗透性土壤k1,该边坡受到不同降雨强度的影响:r1=1.08cm/h和r2=10.8cm/h。不同降雨强度下的安全系数见图4。

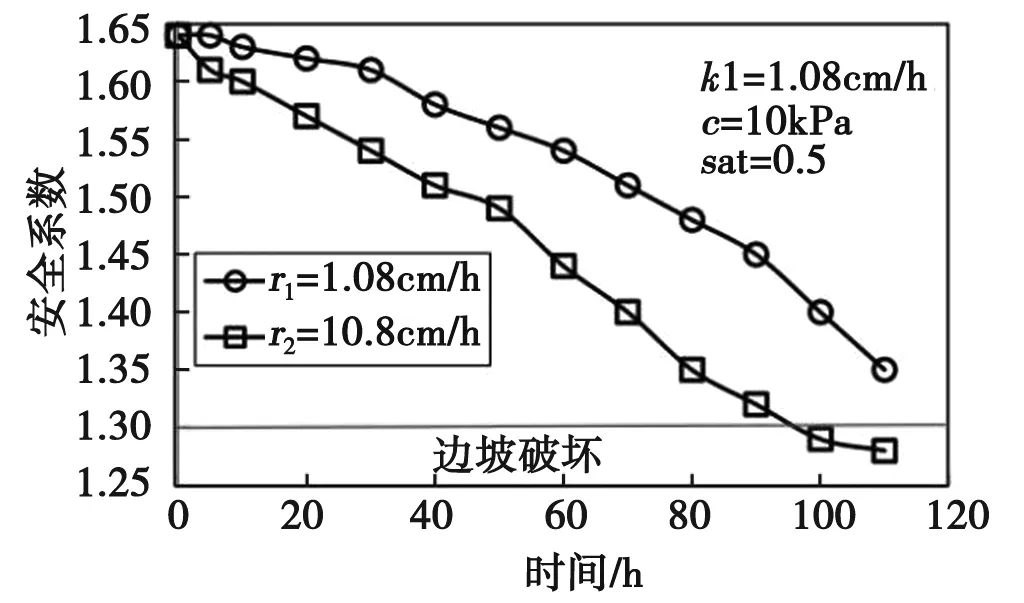
图4 不同降雨强度下的安全系数

从图4可以看出,降雨越大,FOS下降越快,导致边坡失稳的速度越快。这种现象还可以用雨水渗透引起的负孔隙压力变化来解释,降雨量越大,渗入边坡的水量越大,进而导致孔隙压力显著增加。

3.3 初始饱和度和剩余饱和度的影响

土壤饱和度是影响边坡初始FOS值的主要因素。如果渗透系数和降雨强度影响降雨期间FOS的下降,则饱和度直接决定降雨开始前边坡的稳定性阈值。对于不同的饱和度,可得到不同的自由空间。由图5和图6可知,降雨期间FOS的变化在低降雨强度或高降雨强度下都有类似的趋势。当考虑残余饱和度时,也可以看到类似的效果。

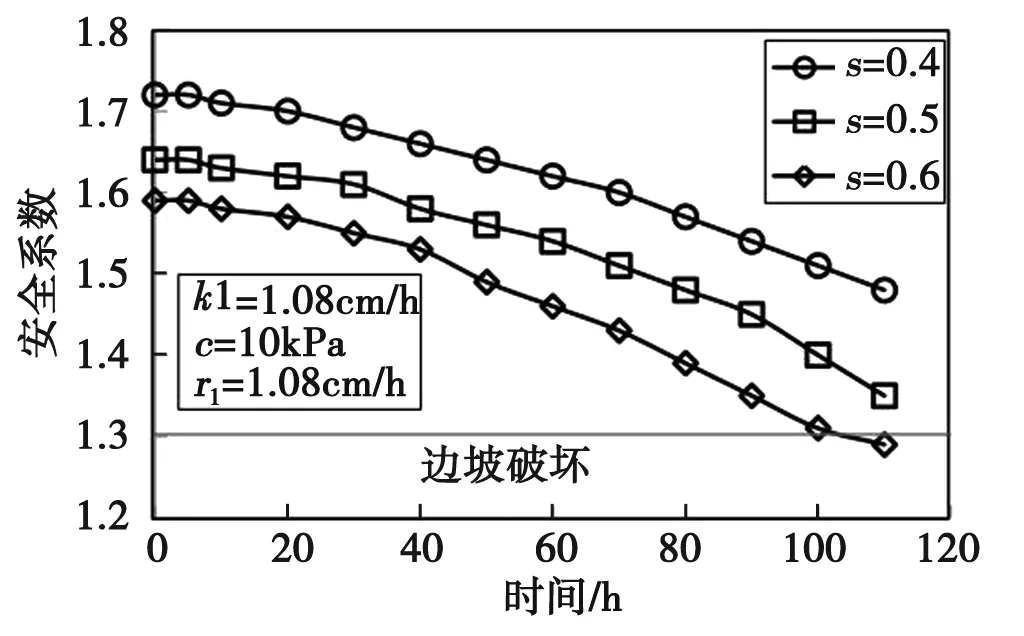
图5 降雨为1.08cm/h时的安全系数

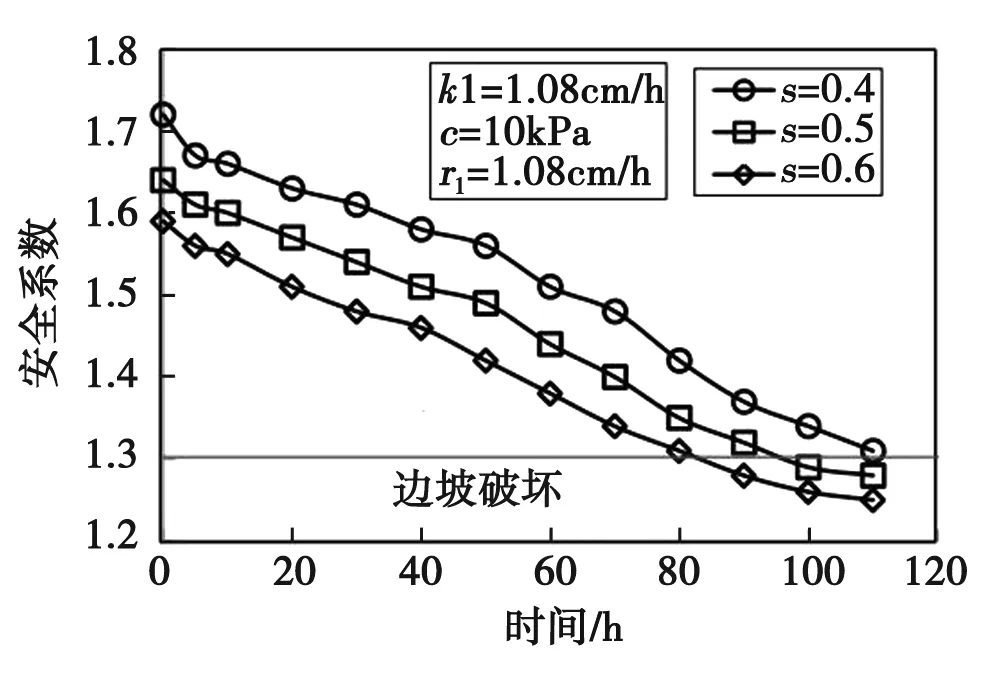
图6 降雨为10.8cm/h时的安全系数

由图7可以看出,当考虑剩余饱和度时,可得到较小的有效饱和度。而剩余饱和度的存在表明,有效饱和度影响孔隙压力分布,进而影响获得的FOS。有效饱和度越低,坡度越稳定。

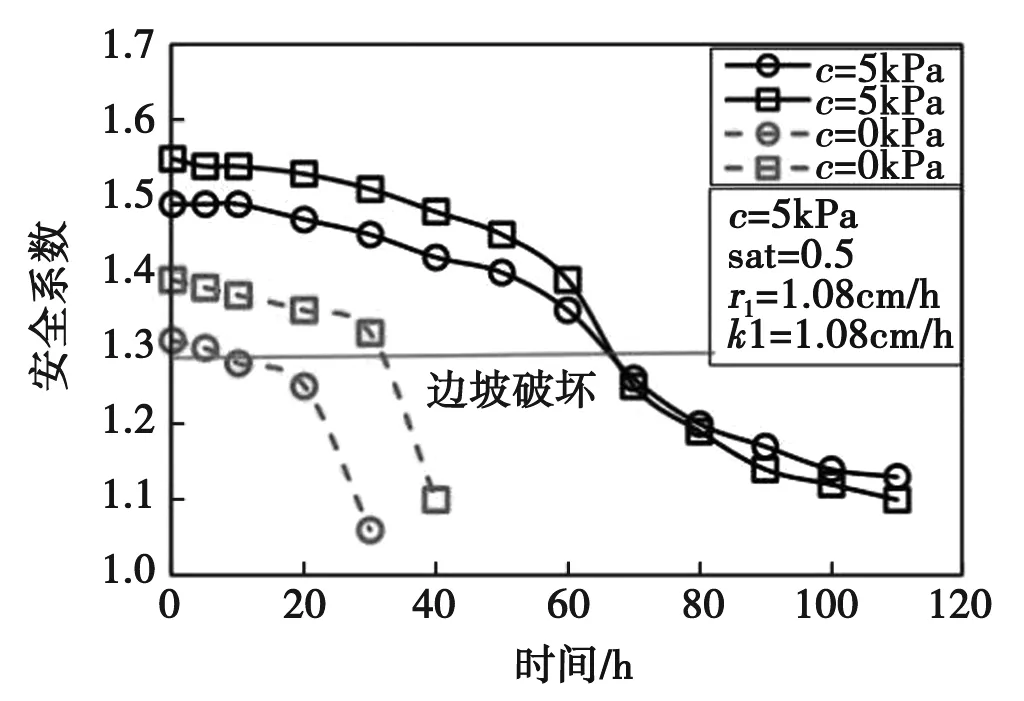
图7 剩余饱和度对安全系数的影响

3.4 土壤黏聚力的影响

为研究黏性的影响,采用饱和度为0.5、渗透性为1.08cm/h、黏性变化较大的土壤,有效黏聚力对安全系数的影响见图8。为了确认孔隙压力的变化是否在这种情况下起重要作用,分析降雨70h后的孔隙压力和相应内聚值的边坡破坏面,见图9。

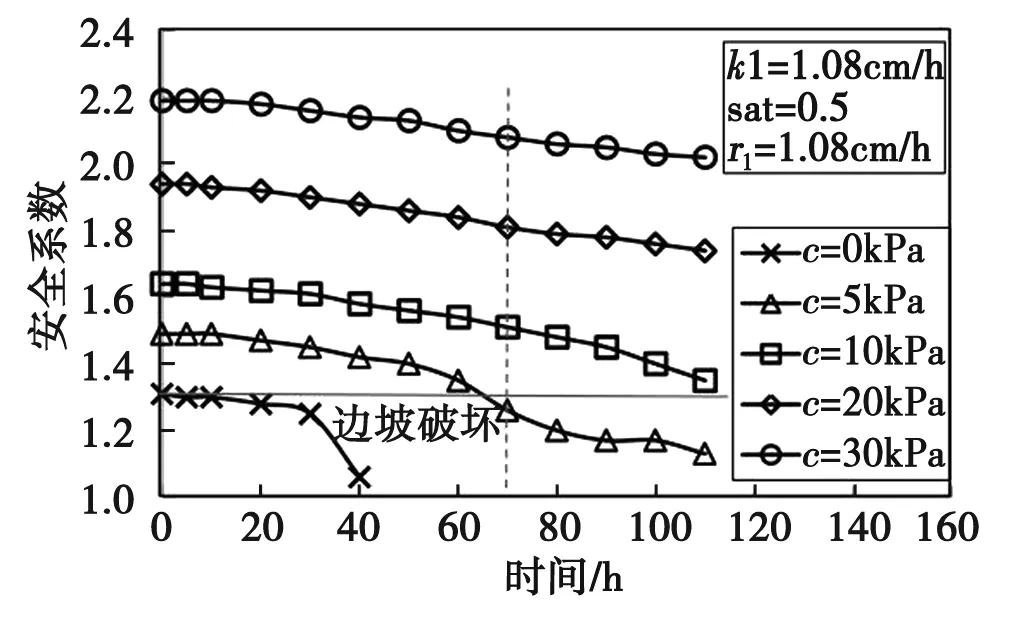
图8 有效黏聚力对安全系数的影响

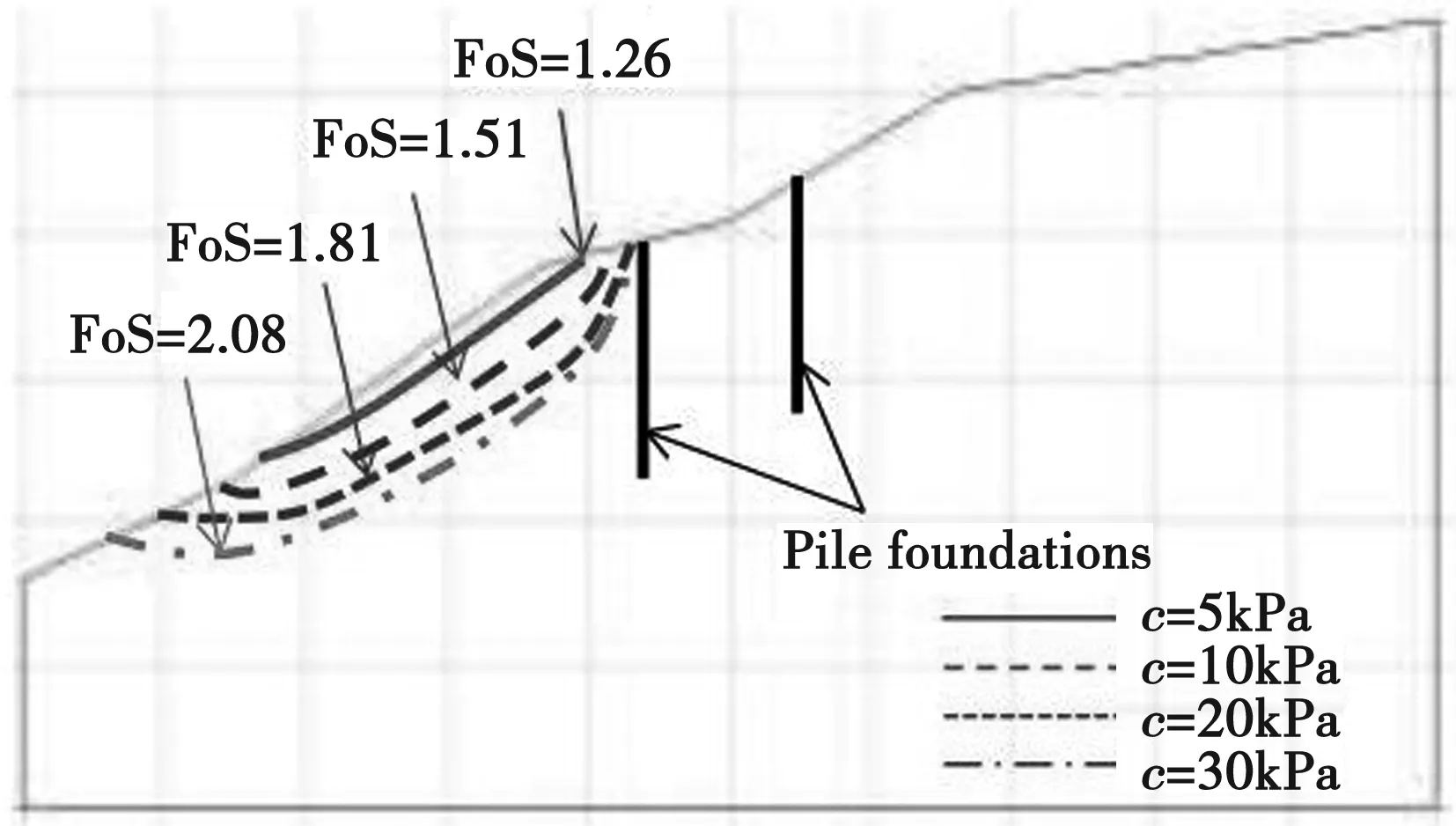
图9 降雨70h后边坡破坏面

由图8可知,降雨期间,FOS减少。在给定的降雨强度下,零内聚力导致5h后边坡失稳,FOS小于1.3,而70h的降雨导致5kPa内聚力的边坡发生破坏。但对于更高的内聚力,FOS的下降速度平缓。

由图9可知,对于所有黏聚力的情况,孔隙压力的分布都是相似的,表明在所有情况下,渗入土壤的水量是相同的。降雨70h后相应内聚值的边坡破坏面,在斜坡上降雨100h(1.08 cm/h)后,20和30kPa内聚力下获得的FOS仍然高于1.8。

4 结 论

通过数值模拟,本文研究了几个水文参数和抗剪强度参数对锦水河典型土边坡降雨诱发边坡失稳的影响,分析了饱和度、渗透率和内聚力在控制初始FOS和渗透过程中的作用。结果表明,饱和度、渗透性和降雨强度对水渗入土壤和负孔隙压力分布有影响。随着渗透性变高,大量雨水渗入土壤,进而增加正孔隙压力。所有参数(即降雨强度、降雨分布和饱和渗透系数)之间存在显著的相互作用,表明在对非饱和边坡进行瞬态分析时,需要对土壤的水力特性进行适当的选择。