导弹产品贮存寿命多源信息融合评估技术综述

张生鹏，马小兵，刘浩然，李宏民

导弹产品贮存寿命多源信息融合评估技术综述

张生鹏1,2，马小兵1，刘浩然3，李宏民1,2

（1.北京航空航天大学 可靠性与系统工程学院，北京 100191；2.航天科工防御技术研究试验中心，北京 100854；3.北京理工大学 管理与经济学院，北京 100081）

面向综合利用导弹产品贮存寿命多源信息的迫切需求，从导弹贮存寿命多源信息的来源、特点、融合模型等3方面进行了综述。分析了导弹产品贮存寿命信息的来源，介绍了自然贮存试验信息、加速贮存试验信息、贮存寿命设计信息的组成内容及优缺点。阐述了导弹贮存寿命多源信息的阶段性、层次性和多源性的特点。对贮存寿命多源信息融合的功能模型、融合层次与算法模型，对加权平均法、贝叶斯融合法、神经网络法、D-S证据理论等方面的应用研究进行了总结。随后，提出了贮存寿命多源信息融合功能模型，涵盖信息源、单元信息融合、系统信息融合、辅助支持系统等模块。最后，针对当前贮存寿命多源信息融合技术研究存在的问题，对未来研究方向进行了展望。

导弹产品；贮存寿命；多源信息；融合评估；功能模型；融合层次；算法模型

现代高技术战争特点如战争的突发性、高强度和高效性，都要求导弹武器装备必须保证和提高其战备完好性、任务成功性。目前，在导弹各型号产品研制过程中，重点关注的一项战技指标就是产品贮存若干年后的可靠度。如何通过科学有效的方法验证评估导弹产品的贮存寿命，为导弹定型、服役与延寿提供依据，是急需解决的关键技术[1]。

在导弹研制使用过程中，为验证或评估导弹产品的贮存可靠性指标，主要采取现场自然贮存试验、实验室加速贮存试验和贮存失效物理分析等3种途径[2]。美国和俄罗斯对此进行了深入广泛的技术方法研究和工程实践[3]，处于世界领先地位。美国的做法是，从产品交付后就制定计划，对现场自然贮存环境下的导弹相关寿命指标进行定期监测，以评估产品的贮存寿命。这种方式试验周期较长，但得到的结果可信度非常高。俄罗斯主要通过加速寿命试验开展产品的寿命评估工作，加速试验可以有效缩短试验周期，但是由于导弹系统构造极其复杂，故障模式和失效机理繁多，因此难以构建准确的加速寿命模型，其准确性一直受到质疑。

目前国内虽然开展了大量的自然贮存试验和加速贮存试验，但是由于贮存数据具有总体数据量大、单个参数有限、变化规律各异的特点，数据缺乏、评估困难的问题仍然普遍存在。一方面，导弹贮存试验样本量少，测试数据有限，自然贮存试验数据的积累时间较长，加速贮存试验又存在一定的局限性，因此不能完全满足导弹产品贮存寿命评估的高准确率要求，特别是针对导弹系统级产品的贮存寿命试验，由于经费、环境条件等因素的限制，不可能开展大量的贮存寿命试验和获取大量的现场数据，因此获取的特征参量极为有限；另一方面，贮存数据存在“非理想数据”，导弹寿命周期长，全寿命数据多，但是经常存在数据不完善，数据量不平衡等问题，对于典型控制系统产品（如惯导、平台等），可进行多次非破坏性测试，测试数据较多，而安全机构与火工品等则只能进行破坏性测试，整体上表现为数据很少，因此没有一个可以刻画不同参数的变化趋势的统一模型。

实际上，在导弹装备定、延寿工程中，导弹产品贮存寿命信息并不仅仅源于自然贮存试验和加速贮存试验的结果，在一定条件下还包括其他所有能够反映该产品贮存期的相关信息，包括设计、试验、使用等各个阶段的贮存寿命信息，分系统级、单元级各个层次的贮存寿命信息，相似产品历史数据、解剖分析信息、设计裕量信息、贮存寿命设计信息等。为了解决当前贮存寿命评估工作中的难题，多源信息的融合利用问题越来越受到重视[4-5]。

本文分析了导弹产品贮存寿命多源信息的来源及特点，介绍了贮存寿命多源信息融合的功能模型、融合层次和算法模型，提出了贮存寿命多源信息融合模型及重点研究方向。

1 导弹贮存寿命多源信息的来源

贮存寿命信息是实施定、延寿工程的基础，是进行贮存期设计、试验、管理的重要依据。导弹贮存寿命多源信息按照信息来源的不同可以分为3类：自然贮存试验信息、加速贮存试验信息和贮存寿命设计信息。各类贮存寿命信息源的组成如图1所示，各类信息源特点比较见表1。

图1 导弹产品贮存寿命信息来源及组成

表1 导弹产品贮存寿命信息内容

2 贮存寿命多源信息的特点分析

导弹产品贮存寿命数据收集的工作量很大，获取贮存寿命数据所需要的费用也较大，因此应尽可能地利用数据，并从中提取尽可能多的信息。

为了全面了解和有效管理、利用贮存寿命信息，需要关注导弹贮存寿命多源信息的三维特点（见图2）。

1）贮存寿命信息的阶段性。产品寿命周期各阶段的设计制造、试验验证及服役使用过程都是贮存寿命信息的产生源。以试验验证阶段为例，贮存寿命数据来源包括加速贮存试验及自然贮存试验等，然而在型号工作中，人们往往仅使用单一的加速贮存试验数据进行贮存寿命评估，这就导致贮存寿命评估的可信度较低。实际上，按照我国国情，往往是在导弹达到或即将达到设计贮存寿命时，才安排开展加速贮存试验，导弹产品在开展加速贮存试验之前，往往已经有了相当年限的自然贮存服役监测数据。因此，有必要将自然贮存服役监测数据和加速贮存试验数据结合，综合评估产品的贮存寿命。

2）贮存寿命信息的层次性。产品的不同结构层次，包括单元、分系统和系统，均存在不同的贮存寿命信息。由于导弹系统造价昂贵，且贮存寿命试验周期很长，开展系统级自然贮存和加速贮存寿命试验通常需要大量的人力、物力和财力作为支撑，因此不能大量进行试验。与之相反，单元和分系统的贮存寿命试验则要方便得多，通过充分开展单元和分系统的贮存寿命试验，可以获得大量有用的贮存试验信息量。因此，当贮存寿命评估的对象是大型复杂系统时，有必要对单元和分系统的贮存寿命信息加以利用，即将单元、分系统和系统的不同贮存寿命试验信息相融合，以综合评估系统的贮存寿命。

3）贮存寿命信息的多源性。除了研制、试验和服役现场获取的贮存寿命信息外，还有很多其他来源的信息需要充分加以利用，如相似产品历史数据、解剖分析信息、设计裕量信息等，充分利用其中的有用信息，能够减少试验成本，同时提高评估结果的准确率。例如，在导弹产品的外观和功能设计过程中，新产品通常会借鉴已有产品或相似产品的参数特点，对外观尺寸或功能参数作出部分调整。因此，相似产品的历史数据、设计信息等能够粗略反映出新产品的寿命信息，在对导弹产品进行贮存寿命评估时，应综合考虑这类信息。

3 贮存寿命多源信息融合模型

多源信息融合的概念和方法一开始主要应用于军事范围内[6]。21世纪以来，该方法逐渐从军事领域向民用领域发展，信息的类型、来源、融合技术等得到更深层次的发展。模型是贮存寿命多源信息融合的核心问题，包括功能模型、融合层次和算法模型。

3.1 功能模型

功能模型展示了多源信息融合系统中各模块的功能和相互作用关系等。现有功能模型包含2种类型：一种是针对处理对象的模型，例如JDL（Joint Directors of Laboratories）模型、瀑布模型和混合模型等；另一种是针对融合过程的模型，例如情报环模型和Boyd控制回路模型。其中，JDL模型[7]及其衍化版本[8]的地位非常重要，应用范围包括军事和民用领域。2002年，Blasch等[9]在基本的JDL模型基础上提出了JDL-User模型，如图3所示。

图3 JDL-User模型示意

3.2 融合层次

功能模型展示了融合模型各组成部分的关系，而融合层次从融合对象的角度出发，明确了信息融合在什么层次上进行。通常来讲，信息融合存在3个层次，分别是数据层、特征层、决策层[10]。

3.2.1 数据层融合

数据层融合首先将多个批次或多个产品在不同时刻的试验数据直接融合，之后就是融合数据的特征提取，并判断其贮存寿命属性，最终输出结果是单元贮存寿命参数的估计值或分布函数，具体流程如图4所示。数据层信息融合常采用加权平均和聚类等方法，它直接对试验数据进行处理，因此可以增大融合结果的可信度。然而，数据层融合也存在一些缺点，相比其他融合层，它需要承受较大的计算负担，并且数据本身存在测量误差等不确定性。

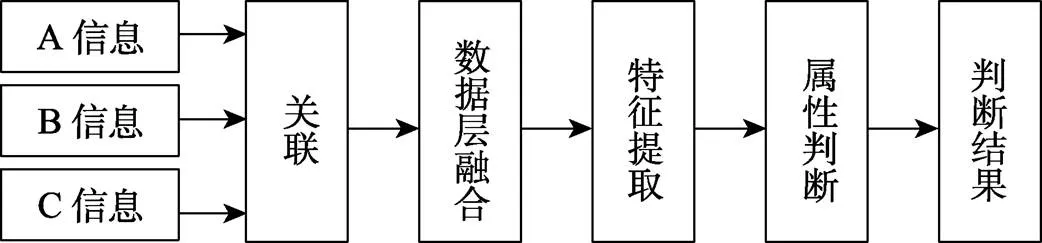
图4 数据层融合流程

3.2.2 特征层融合

特征层融合的对象是特征量，包括从原始数据提取的特征向量和已有的贮存寿命特征量（例如底层折入的MTTF、失效率，以及利用试验数据提取的贮存寿命等）。首先根据内在关系将它们互相组合，其次融合这些组合，得到相应的贮存寿命特征向量，最后做出基于联合贮存寿命特征向量的属性说明，具体流程如图5所示。目前，特征层信息融合方法涵盖了贝叶斯融合、神经网络以及模糊理论等多种方法，其中贝叶斯融合和神经网络应用极为广泛。其优势在于通过提取原始信息的特征，能够降低计算负担，并提高运算性能。

3.2.3 决策层融合

决策层融合是指对不同类型的多源信息分别进行处理，生成针对同一产品的多个贮存寿命评估结果，随后这些结果会被融合中心进行关联处理，输出一个关于该产品贮存寿命的综合判断结果，融合流程如图6所示。决策层融合是对多个评估结果进行融合，因此一些常见的不确定性理论，如D-S证据理论、模糊理论等，都可以作为决策层信息融合的方法，其中D-S证据理论是使用最广泛的算法。

图5 特征层融合流程

图6 决策层融合流程

3.3 算法模型

算法模型是多源信息融合的数学逻辑，在实现贮存寿命信息融合评估的过程中，需要根据融合对象和评估环境的不同，使用不同的算法模型，用以指导相应方法的使用和优化组合。经典的算法包括加权平均法、贝叶斯融合法、神经网络法和D-S证据理论，不同融合算法的比较见表2。

表2 信息融合算法比较

Tab.2 Comparison of information fusion algorithms

3.3.1 加权平均法

如果是信息源的数量，则输出结果应满足：

权重应满足：

图7 加权平均数据融合模型

Fig.7 Weighted average data fusion model

3.3.2 贝叶斯融合法

在特征层信息融合方法中，贝叶斯融合是最常见的一种方法[15-23]。贝叶斯融合考虑在已知多个贮存寿命先验分布的条件下，利用贝叶斯公式计算贮存寿命的后验分布，进而对产品寿命做出合理评估。

设()为参数的先验分布，(|)为似然函数，则后验分布为：

由于多源信息的存在，相同参数常常对应不同的分布。为了融合不同的分布，可以采用线性融合方法和几何融合方法，其表达式分别为：

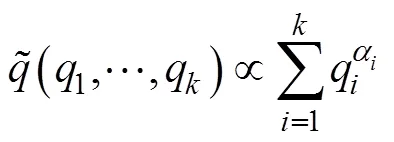
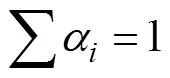
针对原始数据较为匮乏的情况，文献[24-28]考虑了各类先验分布，应用贝叶斯融合方法得到综合性的寿命评估结果。在国内的研究中，文献[29]探索出了一种将贝叶斯理论与仿真相结合的信息融合方法。文献[30]研究了采用贝叶斯方法，通过加速贮存试验及外场试验信息进行寿命推断的问题。

3.3.3 神经网络法

神经网络是一种由大量具有非线性映射能力的神经元相互连接和相互作用而成的模型[31-34]。权系数将这些包含信息的神经元进行连接形成网络，网络本身具有高容错性和鲁棒性。神经网络对原始数据进行加工，从而建立分类规则，这一过程最终导致网络权系数具有不同取值。同时，神经网络采用特殊的算法进行离线或在线学习，以获得特征信息，并建立不确定性推理机制。基于此，神经网络能够实现特征融合和再学习。当多个规则在逻辑推理过程中形成联合规则时，就可以实现信息融合。

3.3.4 D-S证据理论

D-S证据理论是贝叶斯融合的进一步发展[35-36]。贝叶斯融合法在处理不确定性时，需要先验概率的输入，而D-S证据理论可以有效地处理这种由先验概率未知引起的不确定性[37]。因此，在缺乏信息或面临似是而非情况时，D-S证据理论能够更好地揭示信息的含义。

之后，通过均匀分配的思想得到的赌博概率：

利用上式就可以得到系统寿命的概率分布，进而对产品寿命进行评估决策。

目前，D-S证据理论常常被用来将各个决策根据一定的规则按照不确定度进行组合，从而完成不确定推理。文献[38]利用D-S证据理论的不确定度来处理输入图像质量的变化，能够有效融合多种生物特征模态。文献[39]在剩余寿命预测期间的每次迭代中，更新Dempster-Shafer证据的基本概率分配，以此来组合预测结果，提高最终预测的准确性。文献[40]运用D-S证据理论，将多个聚类方法进行融合，以得出轴承的健康指数，并进一步估计其剩余寿命。

在国内，文献[41]运用D-S证据理论将发动机各部件的自然贮存试验、加速贮存试验和专家综合评价等主、客观信息进行了融合。文献[42]提出了一种利用D-S证据理论预测电力设备寿命的方法。文献[43]提出了一种结合D-S证据理论和贝叶斯理论的方法，用于航天设备的寿命预测。

目前在贮存寿命评估过程中已开展了部分贮存信息融合技术的研究工作，并且取得了一定学术成果，积累了有效的工程实践经验。然而，当前研究工作尚未形成一个完整的导弹产品贮存寿命多源信息融合评估体系，缺乏合理、可行的技术途径，影响和制约了贮存寿命多源信息融合评估在型号中的应用。

4 贮存寿命多源信息融合策略及模型构建

针对导弹产品多源贮存寿命信息，以经典信息融合功能模型为基础，对功能模型的流程阶段和处理环节进行合理科学的改进与完善，已成为当前亟待研究的方向。本文提出了贮存寿命多源信息融合功能模型，如图8所示。该功能模型与贮存可靠性“金字塔”评估模型[44]相协调，首先综合利用现有的多种信息融合技术，融合各单元不同来源的贮存寿命信息，得到单元的贮存寿命评估结果；然后对各单元的贮存寿命进行融合，形成对导弹系统贮存寿命的融合评估结果，能够保证融合系统的高效与准确。

贮存寿命多源信息融合功能模型主要包括信息源、单元信息融合、系统信息融合、辅助支持系统等几个模块：

图8 贮存寿命多源信息融合评估功能模型

1）信息源模块是贮存寿命评估的基础和前提，需要全面收集与所研究产品相关的贮存寿命信息，包括贮存寿命信息、贮存环境条件信息、产品组成及特性信息等。

2）单元信息融合模块包括单元特征层信息融合模块和单元决策层信息融合模块。单元特征层信息融合主要是针对导弹基础产品（如器件、结构件等），通过融合全寿命周期不同阶段的贮存寿命信息，例如贮存状态监测/定期检测数据与加速贮存试验数据，实现贮存寿命的高置信度评估。单元决策层信息融合对接受到的相似产品历史数据、解剖分析信息、设计裕量信息等多源信息进行融合，并输出最终的结果。

3）系统信息融合模块包括系统特征层信息融合模块和系统决策层信息融合模块。系统特征层信息融合对多源信息从单元到系统进行逐层综合。系统决策层信息融合通过构建证据网络（EN）模型，将各单元贮存性能的不确定性传递到整个系统中，并实现对系统贮存寿命的高准确率评估。

4）辅助支持系统包括数据库管理系统、人机交互、智能运维、备品备件管理等部分。

5 展望

多源信息融合技术的功能模型和一系列融合算法，能够有效地解决导弹产品贮存寿命评估中的一些难题。然而，当前贮存寿命多源信息融合技术研究仍然面临许多未解决的问题和挑战，后续需重点关注以下几方面的研究工作。

1）单元多阶段贮存寿命信息融合评估方法研究。在导弹产品全寿命周期的各个阶段，都会产生与贮存寿命相关的信息，包括自然或加速贮存试验信息以及服役期间的数据等。为了有效地处理这些贮存寿命信息，并扩大信息处理的时间范围，需要研究针对产品研制、试验和服役等阶段的贮存寿命信息进行融合的方法，对历史数据和当前试验数据进行时间一致性处理，并采用适当的算法，以提高评估精度。

2）单元多源贮存寿命信息融合评估方法研究。导弹产品的贮存寿命信息不仅仅源于加速贮存试验和自然贮存试验，还源于相似产品历史贮存数据、设计裕量信息等贮存寿命设计信息。信息融合可以扩大信息处理的空间范围，针对相似产品历史数据、解剖分析信息、设计裕量信息等多源信息融合问题，需要研究单元多源贮存寿命信息融合评估方法。采用信息融合技术中的多种方法，包括专家系统、模糊集理论和D-S证据理论等，以减少现场试验量，并提高评定结果的准确度。

3）系统级产品贮存寿命信息融合评估方法研究。在导弹单元、分系统、系统等不同层级上都存在着相关贮存寿命信息。通过综合多层次信息得到的贮存寿命评估结果，其准确度将比单一的分系统贮存寿命评估结果高很多。信息融合可以扩大信息处理的层次范围，针对单元-系统等多层次产品贮存寿命信息融合问题，需要研究基于竞争失效的系统贮存寿命融合评估及基于证据网络（EN）的系统贮存寿命融合评估等相关技术和方法。

[1] 张生鹏, 李宏民, 赵朋飞. 导弹装备贮存寿命加速试验技术体系探讨[J]. 装备环境工程, 2018, 15(2): 92-96.ZHANG Sheng-peng, LI Hong-min, ZHAO Peng-fei. Accelerated Testing Technology System for Storage Life of Missile Equipment[J]. Equipment Environmental Engineering, 2018, 15(2): 92-96.

[2] 孟涛, 张仕念, 易当祥. 导弹贮存延寿技术概论[M]. 北京: 中国宇航出版社, 2013. MENG Tao, ZHANG Shi-nian, YI Dang-xiang. Introduction to Missile Storage Life Extension Technology[M]. Beijing: China Aerospace Press, 2013.

[3] 王浩伟, 滕克难, 吕卫民. 导弹贮存延寿试验关键技术及研究进展[J]. 含能材料, 2019, 27(12): 1004-1016. WANG Hao-wei, TENG Ke-nan, LYU Wei-min. Review on Key Technologies for Missile Storage and Life-Extens­i­on Test[J]. Chinese Journal of Energetic Materials, 2019, 27(12): 1004-1016.

[4] 方艮海. 产品可靠性评估中的多源信息融合技术研究[D]. 合肥: 合肥工业大学, 2006. FANG Gen-hai. Research on Multi-Source Information Fusion Technology in Product Reliability Evaluation[D]. Hefei: Hefei University of Technology, 2006.

[5] 庄钊文, 郁文贤, 王浩, 等. 信息融合技术在可靠性评估中的应用[J]. 系统工程与电子技术, 2000, 22(3): 75-77. ZHUANG Zhao-wen, YU Wen-xian, WANG Hao, et al. Information Fusion and Application in Reliability Assessment[J]. Systems Engineering and Electronics, 2000, 22(3): 75-77.

[6] 潘泉, 程咏梅, 梁彦. 多源信息融合理论及应用[M]. 北京: 清华大学出版社, 2013. PAN Quan, CHENG Yong-mei, LIANG Yan. Multi- source Information Fusion Theory and Its Applications[M]. Beijing: Tsinghua University Press, 2013.

[7] WHITE F E. Data Fusion Lexicon[C]// Joint Directors of Laboratories, Technical Panel for C3, Data Fusion Sub- panel. San Diego: Naval Ocean Systems Center, 1987.

[8] STEINBERG A N, BOWMAN C L. Revisions to the JDL Data Fusion Model[M]. Florida: CRC Press, 2017: 65-88.

[9] BLASCH E P, PLANO S. JDL Level 5 Fusion Model: User Refinement Issues and Applications in Group Tracking[C]// Proc Signal Processing, Sensor Fusion, and Target Recognition XI. Orlando: SPIE, 2002.

[10] 李洋, 赵鸣, 徐梦瑶, 等. 多源信息融合技术研究综述[J]. 智能计算机与应用, 2019, 9(5): 186-189. LI Yang, ZHAO Ming, XU Meng-yao, et al. A Survey of Research on Multi-Source Information Fusion Technology[J]. Intelligent Computer and Applications, 2019, 9(5): 186-189.

[11] YAN Zhong-zhen, YAN Xin-ping, XIE Lei, et al. The Research of Weighted-Average Fusion Method in Inland Traffic Flow Detection[C]// ICICA 2011. Heidelberg: Springer Berlin Heidelberg, 2011.

[12] OKASHA N M. An Improved Weighted Average Simulation Approach for Solving Reliability-Based Analysis and Design Optimization Problems[J]. Structural Safety, 2016, 60: 47-55.

[13] ELMENREICH W. Fusion of Continuous-Valued Sensor Measurements Using Confidence-Weighted Averaging[J]. Journal of Vibration and Control, 2007, 13(9/10): 1303- 1312.

[14] HUANG Fang-hui, HE Yi-xin, DENG Xin-yang, et al. A Novel Discount-Weighted Average Fusion Method Based on Reinforcement Learning for Conflicting Data[J]. IEEE Systems Journal, 2023, 17(3): 4748-4751.

[15] POOLE D, RAFTERY A E. Inference for Deterministic Simulation Models: The Bayesian Melding Approach[J]. Journal of the American Statistical Association, 2000, 95(452): 1244-1255.

[16] LI Z S, GUO Jian, XIAO Ning-cong, et al. Multiple Priors Integration for Reliability Estimation Using the Bayesian Melding Method[C]// 2017 Annual Reliability and Maintainability Symposium (RAMS). Orlando: IEEE, 2017.

[17] GUO Jian, (STEVEN) LI Z, JIN Jiong-hua. System Reliability Assessment with Multilevel Information Using the Bayesian Melding Method[J]. Reliability Engineering & System Safety, 2018, 170: 146-158.

[18] YANG Le-chang, HE Ke-tai, GUO Yan-ling. A Novel Bayesian Melding Approach for Reliability Estimation Subjected to Inconsistent Priors and Heterogeneous Data Sets[J]. IEEE Access, 2018, 6: 38835-38850.

[19] YANG Le-chang, GUO Yan-ling, KONG Zi-fan. On the Performance Evaluation of a Hierarchical-Structure Prototype Product Using Inconsistent Prior Information and Limited Test Data[J]. Information Sciences, 2019, 485: 362-375.

[20] 杨乐昌, 郭艳玲. 基于贝叶斯混合概率分布融合的系统可靠性分析与预测方法[J]. 系统工程与电子技术, 2018, 40(7): 1660-1668. YANG Le-chang, GUO Yan-ling. Bayesian Melding Approach of Probability Distribution Fusion for System Reliability Analysis and Prediction[J]. Systems Engineering and Electronics, 2018, 40(7): 1660-1668.

[21] LI Ming-yang, HU Qing-pei, LIU Jian. Proportional Hazard Modeling for Hierarchical Systems with Multi-Level Information Aggregation[J]. IIE Transactions, 2014, 46(2): 149-163.

[22] LI Ming-yang, LIU Jian, LI Jing, et al. Bayesian Modeling of Multi-State Hierarchical Systems with Multi-Level Information Aggregation[J]. Reliability Engineering & System Safety, 2014, 124: 158-164.

[23] LI Ming-yang, ZHANG Wei-dong, HU Qing-pei, et al. Design and Risk Evaluation of Reliability Demonstration Test for Hierarchical Systems with Multilevel Information Aggregation[J]. IEEE Transactions on Reliability, 2017, 66(1): 135-147.

[24] PAN Rong. A Bayes Approach to Reliability Prediction Utilizing Data from Accelerated Life Tests and Field Failure Observations[J]. Quality and Reliability Engineering International, 2009, 25(2): 229-240.

[25] HAMADA M, MARTZ H F, REESE C S, et al. A Fully Bayesian Approach for Combining Multilevel Failure Information in Fault Tree Quantification and Optimal Follow-on Resource Allocation[J]. Reliability Engineering & System Safety, 2004, 86(3): 297-305.

[26] GRAVES T L, HAMADA M S, KLAMANN R, et al. A Fully Bayesian Approach for Combining Multi-Level Information in Multi-State Fault Tree Quantification[J]. Reliability Engineering & System Safety, 2007, 92(10): 1476-1483.

[27] GRAVES T L, HAMADA M S, KLAMANN R M, et al. Using Simultaneous Higher-Level and Partial Lower- Level Data in Reliability Assessments[J]. Reliability Engineering & System Safety, 2008, 93(8): 1273-1279.

[28] TOUW A E. Bayesian Estimation of Mixed Weibull Distributions[J]. Reliability Engineering & System Safety, 2009, 94(2): 463-473.

[29] 宋兆理, 贾祥, 郭波, 等. 基于贝叶斯融合与仿真的系统剩余寿命预测[J]. 系统工程与电子技术, 2021, 43(6): 1706-1713. SONG Zhao-li, JIA Xiang, GUO Bo, et al. System Residual Life Prediction Based on Bayesian Fusion and Simulation[J]. Systems Engineering and Electronics, 2021, 43(6): 1706-1713.

[30] 王立志, 姜同敏, 李晓阳, 等. 融合加速试验及外场使用信息的寿命评估方法[J]. 北京航空航天大学学报, 2013, 39(7): 947-951. WANG Li-zhi, JIANG Tong-min, LI Xiao-yang, et al. Lifetime Evaluation Method with Integrated Accelerated Testing and Field Information[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7): 947-951.

[31] WANG Xin, MAO Dong-xing, LI Xiao-dong. Bearing Fault Diagnosis Based on Vibro-Acoustic Data Fusion and 1D-CNN Network[J]. Measurement, 2021, 173: 108518.

[32] AZAMFAR M, SINGH J, BRAVO-IMAZ I, et al. Multisensor Data Fusion for Gearbox Fault Diagnosis Using 2-D Convolutional Neural Network and Motor Current Signature Analysis[J]. Mechanical Systems and Signal Processing, 2020, 144: 106861.

[33] JOHN A, NUNDY K K, CARDIFF B, et al. Multimodal Multiresolution Data Fusion Using Convolutional Neural Networks for IoT Wearable Sensing[J]. IEEE Transactions on Biomedical Circuits and Systems, 2021, 15(6): 1161-1173.

[34] HE Lei, QIAN Wei-qi, ZHAO T, et al. Multi-Fidelity Aerodynamic Data Fusion with a Deep Neural Network Modeling Method[J]. Entropy, 2020, 22(9): 1022.

[35] DEMPSTER A P. Upper and Lower Probabilities Induced by a Multivalued Mapping[J]. The Annals of Mathematical Statistics, 1967, 38(2): 325-339.

[36] SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.

[37] SHAHPARI A, SEYEDIN S A. Using Mutual Aggregate Uncertainty Measures in a Threat Assessment Problem Constructed by Dempster-Shafer Network[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2014, 45(6): 877-886.

[38] NGUYEN K, DENMAN S, SRIDHARAN S, et al. Score-Level Multibiometric Fusion Based on Dempster–Shafer Theory Incorporating Uncertainty Factors[J]. IEEE Transactions on Human-Machine Systems, 2015, 45(1): 132-140.

[39] DONG Han-cheng. Prediction of the Remaining Useful Life of Lithium-Ion Batteries Based on Dempster-Shafer Theory and the Support Vector Regression-Particle Filter[J]. IEEE Access, 2021, 9: 165490-165503.

[40] RAMEZANI S, MOINI A, RIAHI M, et al. A Model to Determining the Remaining Useful Life of Rotating Equipment, Based on a New Approach to Determining State of Degradation[J]. Journal of Central South University, 2020, 27(8): 2291-2310.

[41] 郭宇, 李海阳, 周伟勇, 等. 基于证据融合的固体发动机贮存寿命评估方法[J]. 固体火箭技术, 2021, 44(4): 448-453. GUO Yu, LI Hai-yang, ZHOU Wei-yong, et al. Evaluation Methods for Storage Life of Solid Rocket Motor Based on Evidence Fusion[J]. Journal of Solid Rocket Technology, 2021, 44(4): 448-453.

[42] 孙曙光, 王锐雄, 杜太行, 等. 基于粗糙集与证据理论的交流接触器预期电寿命预测[J]. 电工技术学报, 2020, 35(10): 2158-2169. SUN Shu-guang, WANG Rui-xiong, DU Tai-hang, et al. Expected Electrical Life Prediction of AC Contactor Based on Rough Set and Evidence Theory[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2158-2169.

[43] 丁瑞, 陆宁云, 程月华, 等. 基于D-S证据理论的航天设备寿命预测方法[J]. 中国空间科学技术, 2016, 36(4): 58-66. DING Rui, LU Ning-yun, CHENG Yue-hua, et al. Lifetime Prediction of Aerospace Equipment Based on D-S Evidence Theory[J]. Chinese Space Science and Technology, 2016, 36(4): 58-66.

[44] 周源泉, 翁朝曦. 可靠性评定[M]. 北京: 科学出版社, 1990. ZHOU Yuan-quan, WENG Chao-xi. Reliability Evaluation[M]. Beijing: Science Press, 1990.

A Review on Multi-source Information Fusion Evaluation Techniques for Missile Products Storage Life

ZHANG Sheng-peng1,2, MA Xiao-bing1, LIU Hao-ran3, LI Hong-min1,2

(1. School of Reliability and Systems Engineering, Beihang University, Beijing 100191, China; 2. Aerospace Science and Technology Defense Technology Research and Experiment Center, Beijing 100854, China; 3. School of Management and Economics, Beijing Institute of Technology, Beijing 100081, China)

In response to the urgent need to comprehensively utilize multi-source information of missile product storage life, the sources, characteristics, and fusion models of multi-source information of missile storage life have been reviewed. The sources of storage life information for missile products are analyzed, and the composition and advantages and disadvantages of natural storage test information, accelerated storage test information, and storage life design information are introduced. The characteristics of multi-stage, hierarchical, and multi-source information of missile storage life are elaborated. The functional model, fusion hierarchy, and algorithm model of multi-source information fusion for storage life have been studied, and the application research of weighted average method, Bayesian fusion method, neural network method, Dempster-Shafer envidence theory, etc. has been summarized. Subsequently, a storage life multi-source information fusion functional model was proposed, covering modules such as information source, unit information fusion, system information fusion, and auxiliary support system. Finally, in response to the existing problems in the current research on multi-source information fusion technology for storage life, future research directions are prospected.

missile products; storage life; multi-source information; fusion evaluation; functional model; fusion hierarchy; algorithm model

2023-09-14；

2023-10-08

TG760.89

A

1672-9242(2023)10-0039-08

10.7643/ issn.1672-9242.2023.10.005

2023-09-14；

2023-10-08

张生鹏, 马小兵, 刘浩然, 等. 导弹产品贮存寿命多源信息融合评估技术综述[J]. 装备环境工程, 2023, 20(10): 39-46.

ZHANG Sheng-peng, MA Xiao-bing, LIU Hao-ran, et al. A Review on Multi-Source Information Fusion Evaluation Techniques for Missile Products Storage Life[J]. Equipment Environmental Engineering, 2023, 20(10): 39-46.

责任编辑：刘世忠