线性变截面梁弹性与塑性变形分析

杨晓林 YANG Xiao-lin；李晨曦 LI Chen-xi

（青海大学土木工程学院，西宁 810016）

0 引言

变截面梁是一种在工程领域广泛应用的结构元素，其特点是在纵向方向上具备不同截面形状或尺寸的能力。通过在不同位置上改变截面形状或尺寸，变截面梁能够有效地满足工程中对不同承载力需求的要求。随着现代建筑和桥梁工程的发展，越来越多的工程设计师意识到变截面梁的重要性和潜在优势。变截面梁不仅可以提高结构的强度和稳定性，还能够优化材料的使用和减少构造成本。因此，通过合理设计和应用变截面梁，我们可以实现更加节能、环保和经济的结构设计方案。对于一般的等截面梁的弯曲问题，材料力学已经给出了结果，但受力复杂的梁以及变刚度梁的计算还是比较繁琐的。王延真等采用最小势能原理，分别构建了变截面梁的结构势能和近似形状函数，通过能量原理将二者联系起来，求解得到变截面梁的近似挠度曲线[1]。冯忠磊通过将大变形梁转变为具有两自由度的伪刚体模型，实现了对大变形柔性梁的变形轨迹和变形角度进行计算[2]。周渤等利用改进傅里叶级数法研究两端任意弹性边界条件的连续多段梁，并基于瑞利－里兹法对其进行求解[3]。Gupta 采用有限元方法求解变截面梁结构的各阶固有频率[4]。马一江等基于传递矩阵法，提出了一种计算含多条裂纹变截面简支梁固有频率的方法[5]。徐勇华等提出基于挠度影响线的变截面梁损伤识别探究[6]。崔灿等将一变截面梁划分为若干个子梁，由各子梁段间力和位移的连续条件，研究了变截面梁动力特性[7]。闫维明[8]等基于Euler-Bernoulli 梁理论改进了直接模态摄动方法，形成了完全弹性支承情况下变截面梁振动方程的半解析法。目前，很多学者对于变截面梁的理论分析和模型分析已经做了大量工作，但加载、卸载阶段的实验分析略显不足，本文通过对变截面梁的实验，分析线性变截面梁的弹塑性加、卸载过程中力、位移的时程变化规律与塑性极限荷载，以期为变截面梁的教学与应用提供参考。

1 实验设计

实验采用变截面梁测试其力学性能，变截面梁的尺寸为长700mm，宽14mm，高24mm，其中变截面高12mm，具体尺寸如图1 及图2 所示，并在变截面梁的一面上喷涂散斑点。采用疲劳机进行实验，在距变截面梁两侧各10mm位置处设置两个支座用于支撑变截面梁，在跨中位置（距离两端350mm）进行加载集中力，加载速度为0.1mm/min，通过疲劳机的位移传感器和力传感器测试变截面梁跨中位置所承受的力以及位移。实验全程采用I-SPEED.221 型高速摄像机记录，曝光速率为5000fps，对应的相机镜头选用尼康AF 50mm f/1.8D 定焦镜头，相机正对试验梁的涂散斑一面水平放置，结合新拓三维软件用于观察整个试验过程中变截面梁的位移。

图1 变截面梁的尺寸示意图

图2 变截面梁现场布置图

2 结果与讨论

2.1 力与位移关系曲线

图3 为力与位移关系曲线图，曲线可以分为三个阶段，OA 段为弹性阶段，力与位移呈比例关系，在2000N 卸载后，力与位移的值下降为零。AB 段为屈服阶段，力值增加缓慢（其增加值为115.1N），而位移增加较多（增加值为6.683mm），表明梁进入塑性流动阶段。BC 为卸载阶段，此时变截面梁的力与位移同时减小，仍然呈正比关系。

图3 变截面梁力与位移关系曲线

加载段OA 的斜率为337.95，卸载段BC 的斜率为342.72；其斜率值近似相等，卸载曲线平行于加载曲线。表1给出了力与位移曲线三个阶段的力值与位移值的变化情况。

表1 变截面梁力与位移曲线特征

图4 为变截面梁力、位移与时间的曲线，从图中可以看出力与时间变化曲线分为3 个阶段，位移与时间变化曲线分为2 个阶段。力值在弹性阶段随着时间的增加而增加，增加速率为5.63N/s；而在屈服阶段力值的增加速率为0.255N/s；在卸载阶段随着时间的增加而减小，减小速率为5.64N/s，其速率与荷载的加载速率一致。位移在弹性、屈服阶段内都随着时间的增加而增加，只在卸载阶段随着时间的增加而减小，但不会减小到0，存在6.6mm 的残余位移，其值占最大位移的44.1%。

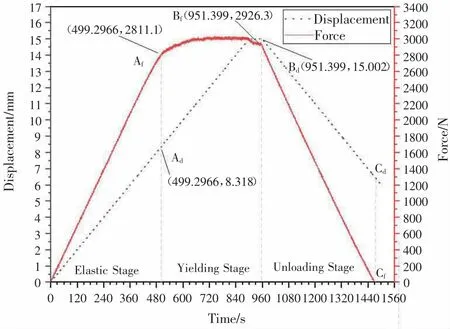
图4 变截面梁力-位移时程曲线

2.2 塑性极限弯矩分析

由实验数据得出屈服荷载为2811.1N。

2.3 DIC 位移云图分析

2.3.1 DIC 位移时程曲线与试验机竖向位移时程曲线的一致性

如图5 所示为DIC 计算梁竖向位移选取的区域，从图中可以看出变截面梁底部的竖向位移最大，越靠近顶部的竖向位移越小。

图5 DIC 计算梁竖向位移选取的区域

如图6 所示为DIC 与疲劳机测得的位移随时间变化的图像，二者测得的位移与时间的趋势一致，都是随着时间的增大，位移先增加后减小，最后减小到一定值后停止。其中，DIC 测得的最大位移为15.001mm，疲劳机位移传感器测得的最大位移为14.8mm，误差为1.34%，表明DIC 位移时程曲线与试验机竖向位移时程曲线的一致性。而DIC位移误差主要来源于以下两个方面：因图像清晰度带来像素坐标转换误差以及图像校准和图像处理过程中标记的区域提取不够精确[9]。

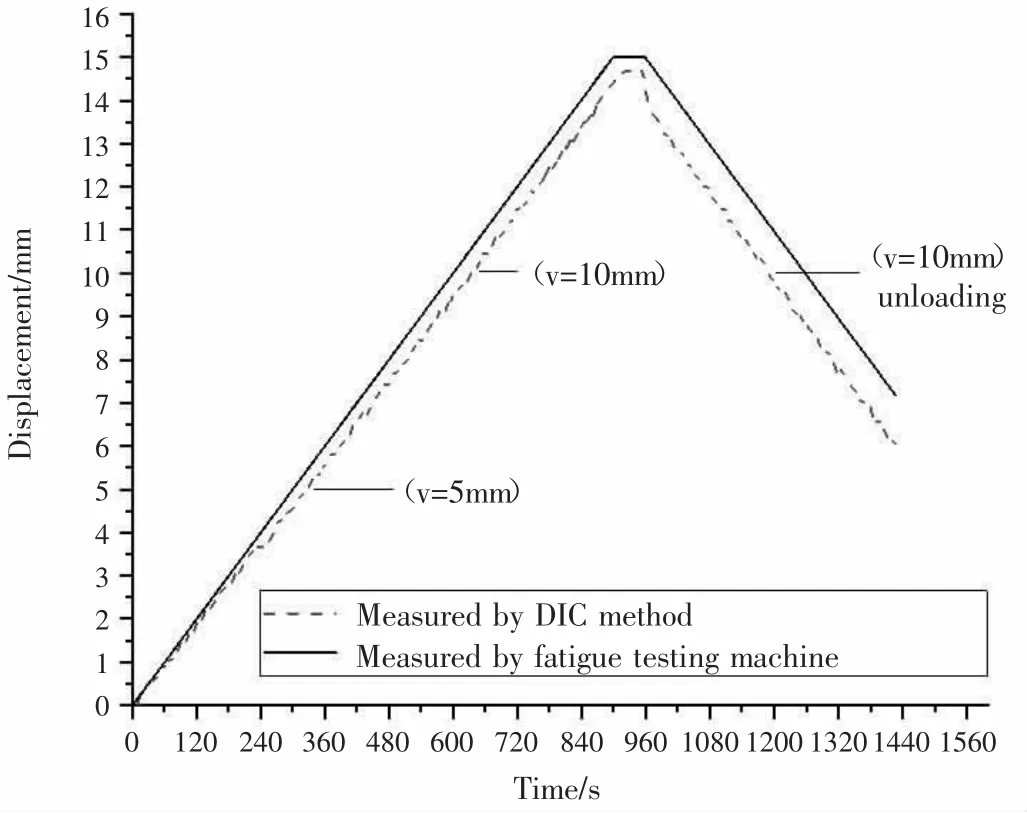
图6 DIC 与疲劳实验机位移随时间变化曲线

2.3.2 水平位移场分析

图7～图9 为变截面梁水平位移场云图，变截面梁在受到集中力时，各阶段水平位移等值线为曲线，可见变截面梁横截面的水平位移不复合平截面假设[10]。

图7 弹性阶段水平位移场（加载段v=5.0mm）

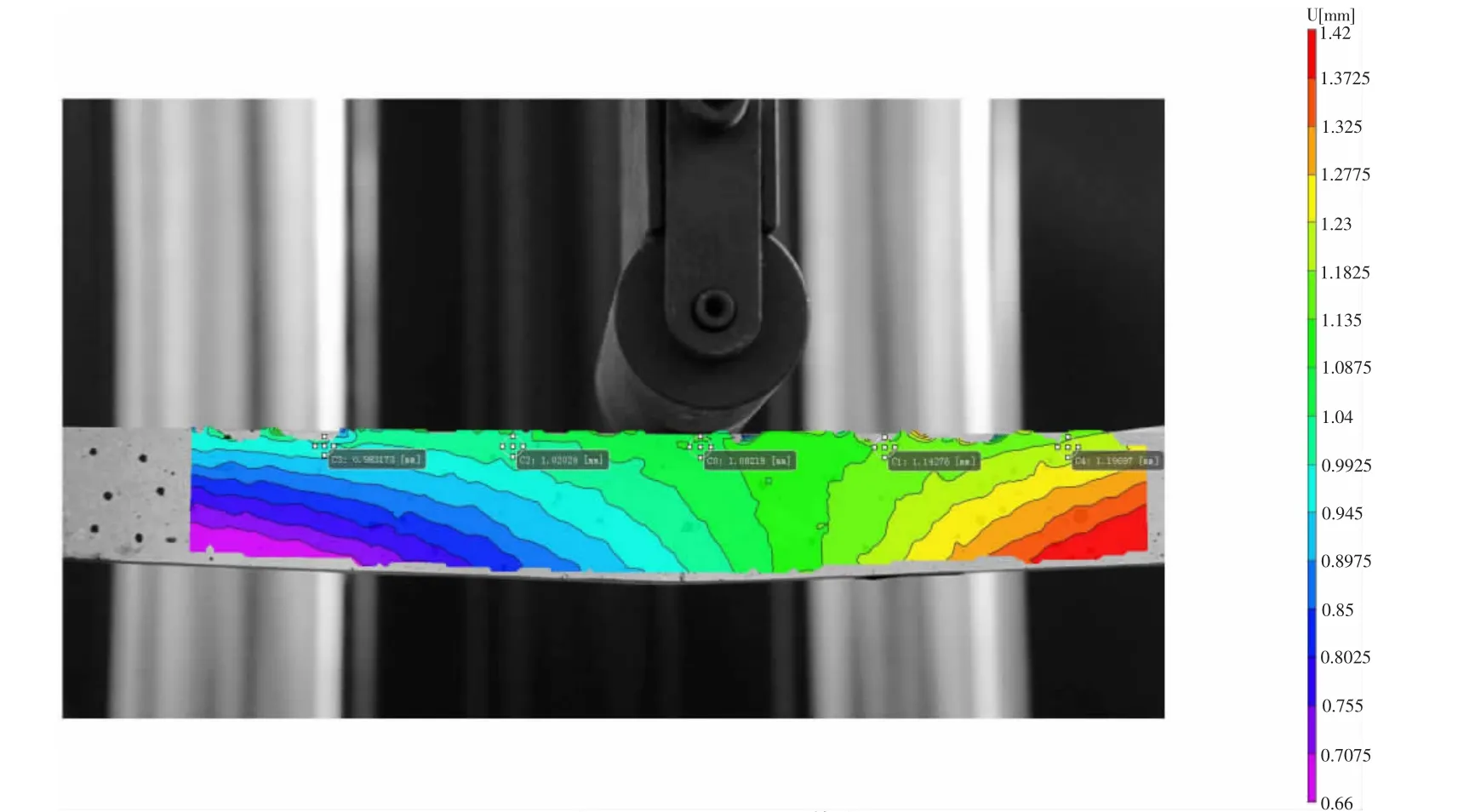
图8 屈服阶段水平位移场（加载段v=10.0mm）

图9 卸载阶段水平位移场（卸载段v=10.0mm）

2.3.3 竖直位移场分析

图10 给出了变截面梁竖直位移场云图，其竖向变形曲线（挠度）可近似用三角正弦函数曲线表达。采用瑞利-里兹法[11]该变截面梁的挠度曲线公式可表达为：

图10 弹性阶段竖直位移场（加载段v=5.0mm）

式中v 为最大竖向位移，Q 为荷载，L 为梁的跨度，E为弹性模量，I0为变截面梁的惯性矩，x1为跨中到梁最左侧的距离。

3 结论

①变截面简支梁的三点弯曲力位移曲线的加载过程可分为弹性、屈服段；卸载曲线平行于加载线，梁卸载后残余位移为6.482mm，占最大位移的43.2%。②卸载曲线近似平行与加载曲线弹性段，屈服阶段荷载增加缓慢变化，但位移仍大幅增加，变截面钢梁进入塑性流动阶段。③DIC位移云图表明，变截面梁的水平位移不满足平截面假设。