以一道中考试题的解答引发的思考
邹翠香


一、试题呈现
题目:如图1,在▱ABCD中,∠DAB=30°。
(1)实践与操作:用尺规作图法过点D作AB边上的高DE;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,AD=4,AB=6,求BE的长。
参考答案:
解:(1)如图2所示线段DE就是所求作的高。
(2)在Rt△ADE中,AD=4,∠A=30°,
∴DE=[12]AD=2。
由勾股定理得
AE=[AD2-DE2]=[42-22]=2[3]
∴BE=AB-AE=6-2[3]
二、试题分析
本题考查了尺规作图——过直线外一点作已知直线的垂线,三角函数、勾股定理,掌握过直线外一点作已知直线的垂线的方法和30度角的余弦值,或利用30度角所对的直角边长等于斜边的一半和勾股定理是解题的关键。通过画图,考查了学生的作图能力及动手能力,明确尺规作图的意义。但是题目中又增加了一个特殊角30°,让图形有了更多不同的作法,考查了学生的创新思维及发散思维能力。
三、学生答题分析
学生的答题情况如下:全市47235人,0分有18251人,满分有12525人,占比分别为38.78%和26.69%,另外占比比较大的是5分,占比13.47%,显示学生要么两问都不会,要么两问都会或者只会做第(2)问;从上面的答题得分情况可以发现有将近六成的考生不会作图,出现部分学生理解错误,作出角平分线或垂直平分线几种错误作法,也有不少学生直接用三角板画出AB边上的高,但欣喜的是出现不少新颖的作法。
四、解法收集
方法1:参考答案是基本尺规作图:过一点作已知直线的垂线,如图2;
方法2:根据直径所对的圆周角是直角,又出现了图3,图4和图5这3种作法;
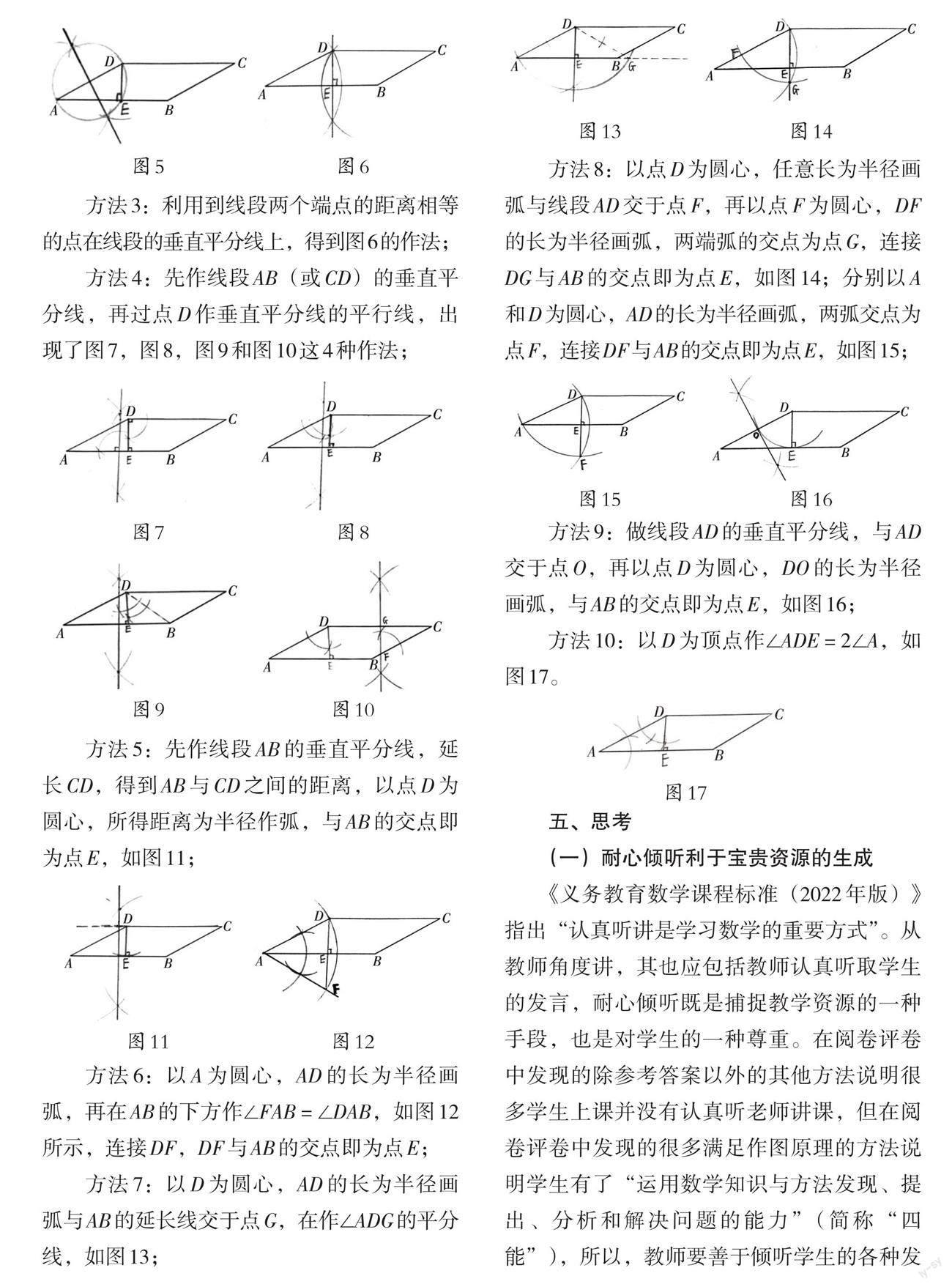
方法3:利用到线段两个端点的距离相等的点在线段的垂直平分线上,得到图6的作法;
方法4:先作线段AB(或CD)的垂直平分线,再过点D作垂直平分线的平行线,出现了图7,图8,图9和图10这4种作法;
方法5:先作线段AB的垂直平分线,延长CD,得到AB与CD之间的距离,以点D为圆心,所得距离为半径作弧,与AB的交点即为点E,如图11;
方法6:以A为圆心,AD的长为半径画弧,再在AB的下方作∠FAB=∠DAB,如图12所示,连接DF,DF与AB的交点即为点E;
方法7:以D为圆心,AD的长为半径画弧与AB的延长线交于点G,在作∠ADG的平分线,如图13;
方法8:以点D为圆心,任意长为半径画弧与线段AD交于点F,再以点F为圆心,DF的长为半径画弧,两端弧的交点为点G,连接DG与AB的交点即为点E,如图14;分别以A和D为圆心,AD的长为半径画弧,两弧交点为点F,连接DF与AB的交点即为点E,如图15;
方法9:做线段AD的垂直平分线,与AD交于点O,再以点D为圆心,DO的长为半径画弧,与AB的交点即为点E,如图16;
方法10:以D为顶点作∠ADE=2∠A,如图17。
五、思考
(一)耐心倾听利于宝贵资源的生成
《义务教育数学课程标准(2022年版)》指出“认真听讲是学习数学的重要方式”。从教师角度讲,其也应包括教师认真听取学生的发言,耐心倾听既是捕捉教学资源的一种手段,也是对学生的一种尊重。在阅卷评卷中发现的除参考答案以外的其他方法说明很多学生上课并没有认真听老师讲课,但在阅卷评卷中发现的很多满足作图原理的方法说明学生有了“运用数学知识与方法发现、提出、分析和解决问题的能力”(简称“四能”),所以,教师要善于倾听学生的各种发言,充分暴露学生的思维过程,在学生的发言中发现有价值的教育因素,开发教学资源,实现师生共同研究、共同发展。
(二)问题引导探究,注重活动经验的积累和学科本质的考查
《义务教育数学课程标准(2022年版)》指出“在尺规作图中,学生应了解作图的原理,保留作图的痕迹,不要求写出作法”。在阅卷评卷中发现很多作图轨迹有想法但图形做的不完整,这个就需要教师在平时的教学中将尺规作图出现的所有满足作图原理的方法都能讲解一下,这个过程不仅能让学生掌握基本的尺规作图,还可以利用所学发现一些新的作法,在上面收集的方法中,每种方法都有考到一些数学知识点。例如:方法2,就考到圆的知识点:直径所对的圆周角是直角,图2还用到平行四边形的性质:对角线互相平分;方法3,就考到垂直平分線的判定:到线段两个端点的距离相等的点在线段的垂直平分线上;方法4,使用了两个基本尺规作图:作垂直平分线和作一个角等于已知角,还考到了平行线的性质;方法5,考到了两条平行线之间的距离:是指从两条平行线中的一条直线上的一点作另一条直线的垂线段的长,还利用了它的2个拓展:①能表示两条平行线之间的距离的线段与这两条平行线都垂直,②平行线间的距离处处相等;方法6和方法7都用到了等腰三角形的性质:三线合一;方法8、方法9和方法10都是∠A=30°的特殊作法,比如方法8作出的△DFG和△ADF是等边三角形,即∠FDG=∠ADF=60°,∴∠AED=180°-30°-60°=90°,即DE⊥AB;方法9利用的是30°所对的直角边等于斜边的一半,∴以AD的一半为半径,点D为圆心作的圆与直线AB相切,即DE⊥AB;方法10与方法8的理由相同。
(三)教学建议
1. 在阅卷评卷中发现有些学生作图工具准备得不太理想,图象不清晰,轨迹忽隐忽现,以后在教学中应该提醒学生所用工具作出的图形要清晰、完整,平时要多些训练作图题,让学生对基本尺规作图熟练掌握。
2. 从本题的尺规作图中,还能发现学生的创新能力,以后在尺规作图的训练中,可以利用特殊角、特殊边等,让学生不仅限于课堂所教的方法去解决问题,培养学生的思维能力,即针对作图题也要进行一题多解训练。
3. 教学生作图时,提醒学生要规范作图,该用圆规的地方要用圆规,不能徒手画弧,用圆规作图时要记得多画两遍,加粗轨迹。
4. 学生的圆规,作图用的铅笔必须是要2B铅笔芯,否则扫描会出现不清晰的情况。
5. 对本题也可以进行一些改编后让学生训练。
改编一:如图18,在▱ABCD中,∠DAB=30°。
(1)实践与操作:用尺规作图法在AD上找到点E使得AE=BE;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,AD=4,AB=6,求DE的长。
改编二:如图18,在▱ABCD中,∠DAB=30°。
(1)实践与操作:用尺规作图法过点D作DE⊥AD交AB于点E;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,AD=4,AB=6,求BE的长。

