摆式摩擦发电机非线性机电耦合建模研究1)

韩勤锴 高 帅 邵卿洋 褚福磊

* (清华大学高端装备界面科学与技术全国重点实验室,北京 100084)

† (米兰理工大学机械学院,意大利米兰 20156)

引言

凭借结构多样、输出稳定、能量转换效率高、成本低、环境适应能力强等优点,摩擦纳米发电机(triboelectric nanogenerators,TENG)在环境振动能量收集中受到广泛关注[1-2].自然环境中大量存在的是低频振动能量.例如,人走路的频率大致在2～3 Hz 之间,海浪波动以及高层或大型建筑的振动频率大都集中在10 Hz 以下甚至更低[3-4].通过合理设计摆长,可有效降低单摆固有频率,使其在低频(甚至超低频)振动激励下即可实现共振,进而大幅提升能量采集器的表现[5-7].因此,结合单摆结构的摩擦发电机(pendulum-type TENG,P-TENG),自然成为学界关注的焦点[8-9].开展输出特性建模与参数敏感性分析,将有助于P-TENG 的结构优化设计,进而推动P-TENG 向工程实用化方向发展[10-11].

开展TENG 输出特性分析的核心是明确输出电压、摩擦电荷和电极距离之间的关系,即V-Q-x关系.采用等效电路方法,Niu 等[12]首次开展这方面的研究.分别针对具有不同结构形式的TENG (包括滑动结构[13]、单电极结构[14]、光栅结构[15]等),建立了相应的输出特性分析模型.为了提升模型的预测表现,不少学者从电荷转移机制[16-17]、接触界面微观形状[18-19]、拓扑结构优化[20-23]和初始残余电荷[24]等多个角度,对TENG 输出特性分析模型进行了持续的改进.但是,现有研究仍然采用线性谐波函数近似电极分离距离的变化.当振动频率接近或等于固有频率时,单摆大幅摆动,引起显著的非线性效应.已有研究证实线性函数近似将使模型产生较大的预测误差[25-27].但这些研究所考虑的非线性效应是由电极之间或介电层与电极之间的非连续碰撞引起的,尚无研究涉及P-TENG 中单摆大幅摆动引起的非线性效应.

因此,本研究开展用于P-TENG 输出特性分析的非线性机电耦合建模.在摩擦发电机理分析的基础上,提出了等效电容模型;结合能量原理和等效电路方法,建立了考虑摆角非线性变化的机电耦合模型.利用谐波平衡法,解析求解P-TENG 的周期稳态输出,并判断结果的稳定性.采用数值积分和动态测试两种手段,验证谐波平衡结果的准确性.通过对比P-TENG 工作带宽和最大输出电流的变化,说明考虑非线性效应的必要性.在此基础上,讨论设计参数(包括激励幅值、阻尼比、间隙长度和电极夹角)对系统动态输出特性的影响.通过构建多种拟合模型,为P-TENG 输出性能设计提供依据.最后,总结论文的结论.

1 非线性机电耦合模型

1.1 摩擦发电机理

所研究的P-TENG 结构如图1 所示,包括扇形单摆、中心轴和圆形基板等.扇形单摆的材质为聚四氟乙烯(PTFE),通过滚动轴承支承在中心轴上,可绕轴心往复摆动.建立轴心O为坐标原点的坐标系O-x-y,单摆质心半径为rp.当P-TENG 受到环境振动激励力Fx(t)时,质心相对平衡位置的摆角为θ,且规定向右为正,如图1 所示.圆形基板上设置左右铜电极,夹角为α.极性不同的单摆和铜电极经过若干次接触滑动后,在其表面将分别带上等量异号的摩擦电荷,并随着滑动次数的增加逐渐达到电荷饱和.因单摆的材质为PTFE,其表面摩擦电荷可以驻留较长时间而不衰减.

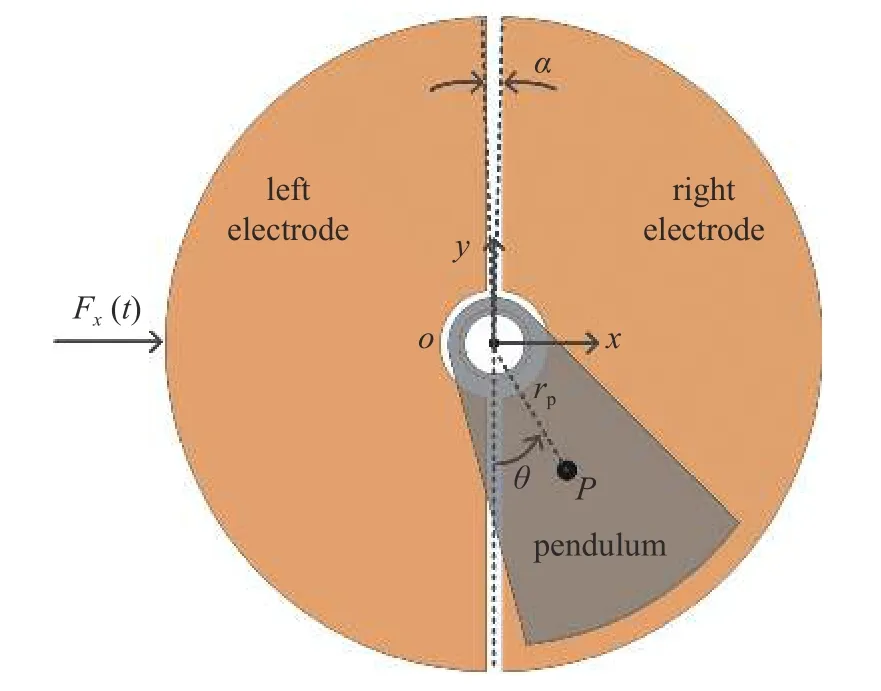
图1 P-TENG 结构图Fig.1 Structure of the P-TENG

左、右电极与扇形PTFE 单摆,共同构成自由层模式TENG.为了便于分析摩擦发电机理,可沿基板圆形环面剖切,截面如图2 所示.假定图2 中(i)为初始位置.根据电荷守恒定律,PTFE 单摆的摩擦电荷量与左电极的摩擦电荷量相等.两电极电势差为零,外电路没有电流产生.当PTFE 单摆相对于基板摆动至位置(ii)时,在静电感应作用下,电荷会通过外电路,从左电极运动到右电极;当PTFE 单摆摆动至位置(iii)时,左电极上的电荷完全移动至右电极,使其与PTFE 单摆表面的电荷量相等.此时,外电路中电流为零.当PTFE 单摆回摆至位置(iv)时,电荷会通过外电路,从右电极移动到左电极.如此循环往复,在外电路中形成交变电流,实现了外部机械能到电能的转换.基于COMSOL 静电场仿真模块,计算了上述4 个位置时,PTFE 单摆与左右电极截面之间的电势差分布,如图3 所示.仿真结果与上述结果具有较好的一致性,从而验证了原理分析的准确性.

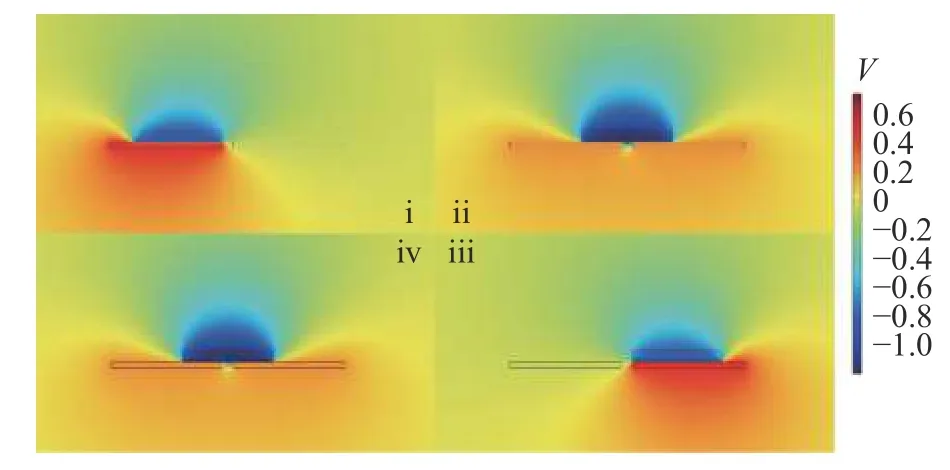
图3 基于COMSOL 的静电场仿真结果Fig.3 Simulation results based on the COMSOL

1.2 等效电容分析与拟合

PTFE 单摆与左右电极组成了一种独立层式可变电容器,可将其简化为如图4 所示带负载Re的等效电路系统.图中Cp-l和Cp-r表示PTFE 单摆与左右电极的电容,二者是串联关系;而与平板式独立可变电容器不同的是,单摆无法完全隔开两个电极,因此还存在Cl-r,表示两个电极之间的电容,与前两者是并联关系.3 个电容值均为摆角θ的函数.鉴于结构的复杂性,基于COMSOL 建立了三维电容仿真模型,如图5 所示.仿真时结构参数如表1 所示.单摆与电极表面的间距为δ=0.2 mm.PTFE 材料的相对介电常数设置为2.引入真空介电常数ε0和长度L=1 m,将计算得到的电容值进行无量纲处理.

表1 电容仿真时P-TENG 结构参数Table 1 Structural parameters of the simulated P-TENG

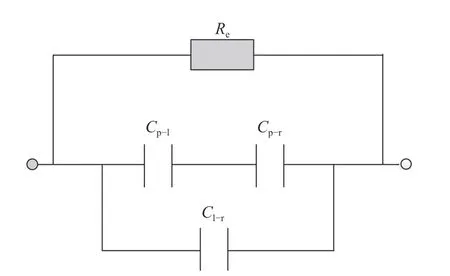
图4 带负载的等效电路系统Fig.4 Equivalent circuit system with external resistance

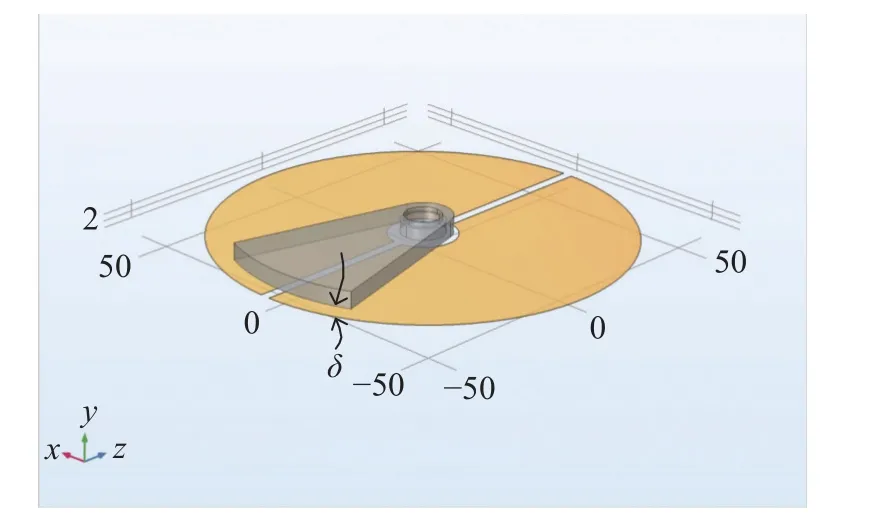
图5 等效电容仿真模型 (单位: mm)Fig.5 The three-dimensional capacitance simulation model based on COMSOL (unit: mm)

通过静电场计算得到无量纲电容值随摆角的变化曲线,如图6(a)所示.当摆角θ由-90°增加至90°时,Cp-l先缓慢降低;在θ=0°附近,快速降低;进而缓慢降低.与之相反,Cp-r先缓慢增加,在θ=0°附近,快速增加;进而缓慢增加.Cl-r几乎保持不变,因此在后续分析中将着重考虑Cp-l和Cp-r.考虑到后续将用到电容倒数值,可采用如下函数进行拟合

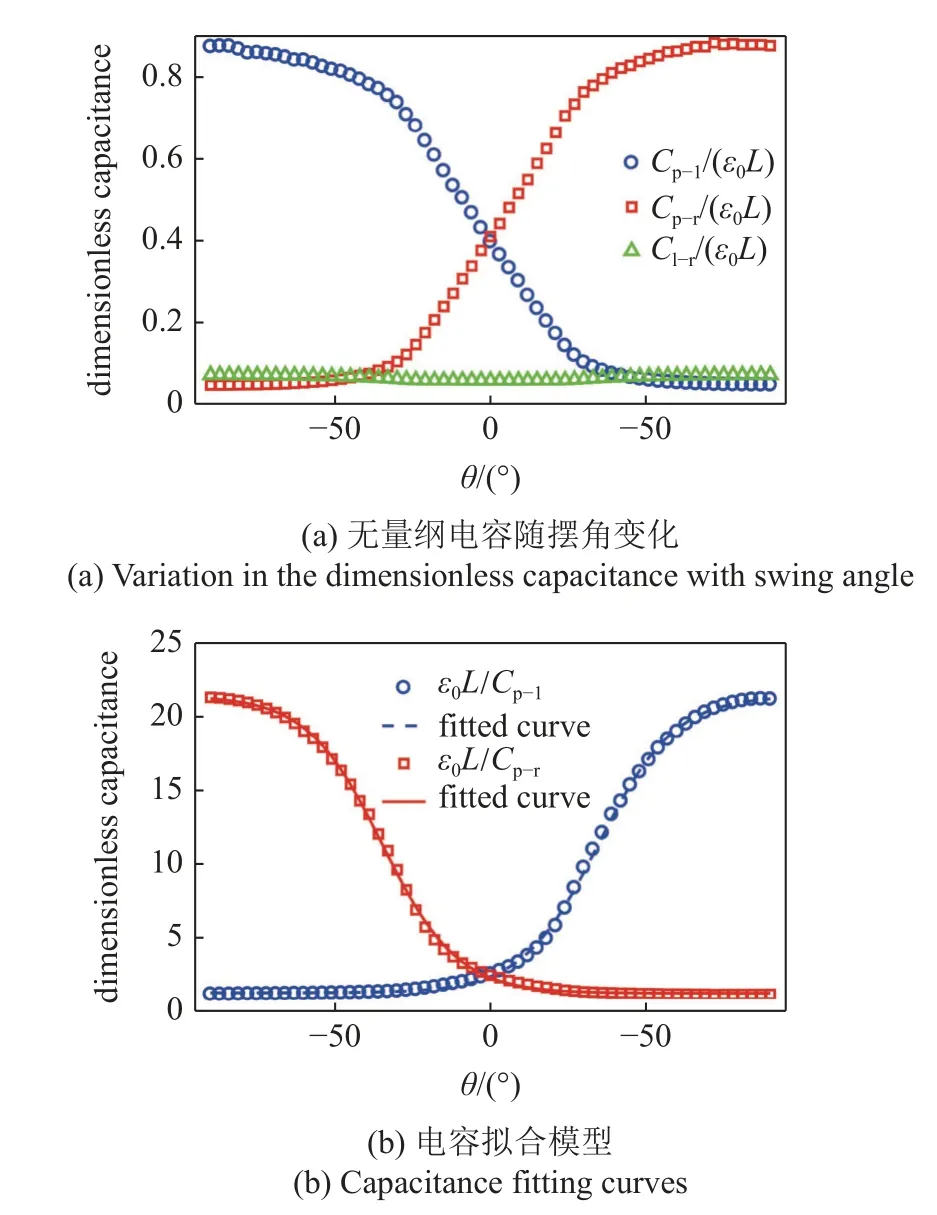
图6 等效电容仿真结果Fig.6 Capacitance simulation results

式中,a1=11.331 1,a2=10.099 7,a3=0.040 9,a4=1.419 0分别为相应的拟合系数.拟合曲线如图6(b)所示.结构尺寸不同,对应的拟合系数值也有所不同.

1.3 解析建模

根据图1 中的几何关系,当滚动角为θ时,可得单摆质心水平和垂向位移为xp=rpsinθ和yp=rp(1-cosθ).假定单摆表面摩擦电荷均匀分布,电荷量为σS,其中σ为摩擦电荷密度,S为单摆表面积.电容Cp-l的极板电荷为Q,电容Cp-r的极板电荷为Q-σS.系统的动能、势能以及耗散能(实为耗散功率)可分别表示如下

式中,mp和Jp表示单摆质量和绕质心转动惯量,g为重力加速度,cp表示系统阻尼系数.考虑外力作用引起的广义力可表示为:Fx(t)=mpax(t),其中ax(t)表示加速度.将式(1)和式(2)代入式(3)～式(5)中,基于拉格朗日方程,并取sinθ≈θ-θ3/6 和cosθ≈ 1-θ2/2,可得P-TENG 的机电耦合方程如下

从式(6)和式(7)可以看出,由于机电耦合效应,使得单摆摆动方程中出现与电荷Q相关项,而电路方程中出现与摆角θ相关的系数.此外,式(6)中还出现了摆角的二次项和三次项(即θ2和θ3),其为非线性效应的具体表现.后续研究中,也将重点讨论非线性效应对系统输出特性的影响.若忽略耦合项对摩擦电荷的影响,在小幅摆角下,系统的固有频率可表示为

采用SolidWorks 求算单摆对质心的转动惯量及质心的半径,得mp=0.019 7 kg,Jp=6.533 kg·mm2,rp=30.612 mm,代入式(8),计算得ω0≈ 2.45 Hz.

将时变加速度激励设定为谐波形式,即ax(t)=ax0cos(ωxt),其中ax0和ωx分别表示激励幅值和频率.引入无量纲时间为τ=ω0t,角位移尺度θ0=π/2,无量纲摆动位移为θn=θ/θ0.无量纲电荷可表示为Qn=Q/(σS).阻尼比ζ=cp/[2(mprp2+Jp)ω0],无量纲激励幅值an=ax0/(Lω02)和频率ωn=ωx/ω0.将上述变量代入式(6)和式(7),可得无量纲化后的机电耦合模型为

2 分析方法

作为数值积分方法的替代方法,谐波平衡法(HBM)可用于求解非线性系统的稳态周期解[28].与经典的摄动法、多尺度法等相比,谐波平衡法的优点是普适性强,对于强非线性系统也可获得满意的结果.将上一节得到的机电耦合方程表示为矩阵形式

其中y=[θn,Qn]T表示自由度向量,A,B,C分别表示系数矩阵,具体表达式如下

Fxq由无量纲化的外部激励力、非线性激励力和机电耦合力组成,可表示为

单摆运动的稳定解可表示为如下Fourier 级数形式

式中,N表示Fourier 级数的阶数,Yk表示系数向量.稳定解对τ的一阶和二阶导数项为

由于不同参数和初始条件下,系统稳态响应解所对应的谐波组合都不同,考虑对系统响应具有显著影响的低阶谐波.不失一般性,可将Fxq分为线性部分G(τ)和非线性部分Fu(τ)的叠加,二者可分别表示为傅里叶级数形式

式中,Gk和Fuk分别为线性和非线性激励力的傅里叶系数向量.将式(14)～式(18)代入式(11),通过运算平衡掉同次谐波项,可得到一组代数方程组.如果取到N次谐波,则可得2(2N+1)个方程,由此可求出包含有N次谐波的近似解.对于第k阶谐波系数,有如下关系

由于非线性力Fu(τ)是自由度y的函数,因此其傅里叶系数Fuk也是Yk的函数.因非线性因素的影响,上式需要数值方法求解.借助Carmeron 等[29]提出的时频变换方法,可以将系统数值响应信号由时域变换到频域,进而可以确定系统响应中所包含的主要频率成分,求解具有高阶截断的Y与Fu级数解形式,即

基于此,非线性代数方程组(见式(19))可通过Newton-Raphson 迭代方法求解.因分叉导致的系统多解区,需借助弧长延拓技术进行有效跟踪[30].尽管谐波平衡法能够求解系统稳态响应,但并不意味着该响应是稳定的.因此,有必要研究周期解的稳定性问题.为了保持频域方法的计算效率,需要开展频域稳定性分析.具体流程可参考文献[25-26].

3 模型验证与对比

3.1 数值积分

采用数值积分和动态测试两种手段,验证所提出的基于HBM 的P-TENG 输出特性分析结果的准确性.仿真和试验测试的P-TENG 参数已在第1 节中给出.表面摩擦电荷密度σ=1 nC/cm2,无量纲激励幅值an=0.005 且频率ωn的变化范围为[0.5,1.5].考虑短路条件(Re≈0 Ω),采用HBM 和数值积分方法(numerical integration,NI)求解单摆角位移和表面电荷,如图7 和图8 所示.其中HBM 解的稳定性判别结果也在图中给出.当ωn由0.5 增加至1 (即为线性系统固有频率)时,摆角和电荷响应曲线均出现向左倾斜的现象.这是由于单摆摆动幅度的增加,系统非线性“软特性”效应增强导致的.HBM 结果与NI 结果吻合较好,初步验证了所提出的输出特性分析方法是可靠的.当谐波次数N由4 增加至6 时,响应峰值有所下降;继续增加N至8 时,响应峰值几乎保持不变,表明低阶谐波对P-TENG 输出特性的影响占主导.后续的分析将取N=6.

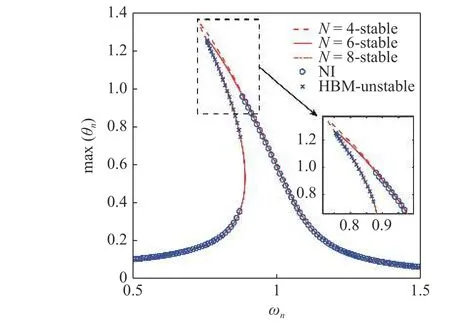
图7 单摆最大摆角随激励频率变化曲线Fig.7 Pendulum angle vs.excitation frequency solved by HBM and NI

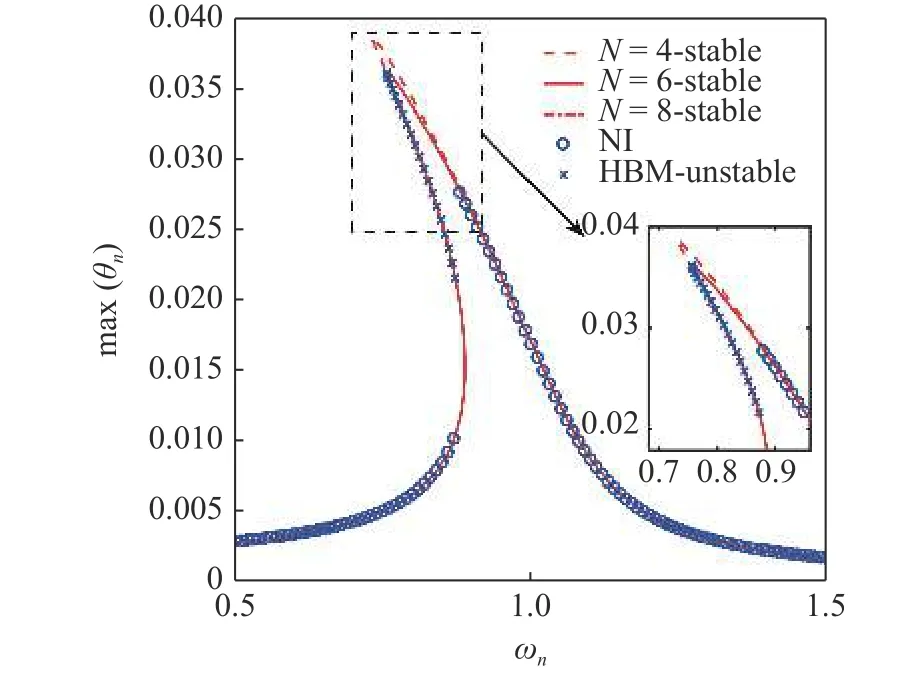
图8 P-TENG 表面摩擦电荷随激励频率变化曲线Fig.8 Surface charge vs.excitation frequency solved by HBM and NI

3.2 动态测试

图9 给出了基于直线电机的动态测试平台,其中P-TENG 样机如图特写所示.直线电机产生周期性的振动激励,其频率和幅值分别由内置的信号发生器和功率放大器控制.P-TENG 的左右电极外接负载电阻,通过静电计和NI 数据采集模块实时采集并记录动态电流,进而通过PC 进行后处理分析,得到P-TENG 的输出特性.动态测试中记录的是流经负载电阻的电流信号,而机电耦合模型中只能得到表面电荷信号,需要计算电荷对时间的微分,以获得实时电流,即

图9 基于直线电机的P-TENG 动态测试平台Fig.9 Dynamic test platform based on a linear motor

同时,需将试验结果进行无量纲化,根据第2 节中定义的电荷和时间尺度,可知需将试验结果得到的电流值除以σSω0.外接负载电阻Re=1 MΩ 时,实测和HBM 计算的输出电流均方根值随激励频率的变化结果如图10(a)所示.当ωn接近或者等于系统固有频率时(即ωn≥ 1),由于“软特性”非线性的影响,输出电流响应曲线有明显向左倾斜的现象,这样对P-TENG 工作频带的拓宽是有利的.试验结果很好印证了HBM 结果,进一步验证了理论模型和所采用的分析方法是合理的.当ωn=0.87 时,实测和HBM 得到的输出电流和功率密度随负载电阻的变化情况如图10(b)所示.随着负载电阻的增加,输出电流先缓慢下降,而后迅速降低;而功率密度则先增加后降低,在Re=200 MΩ 附近取得最大值,约为1500 μW/m2.试验与HBM 结果较为一致,进一步验证了理论模型的准确性.

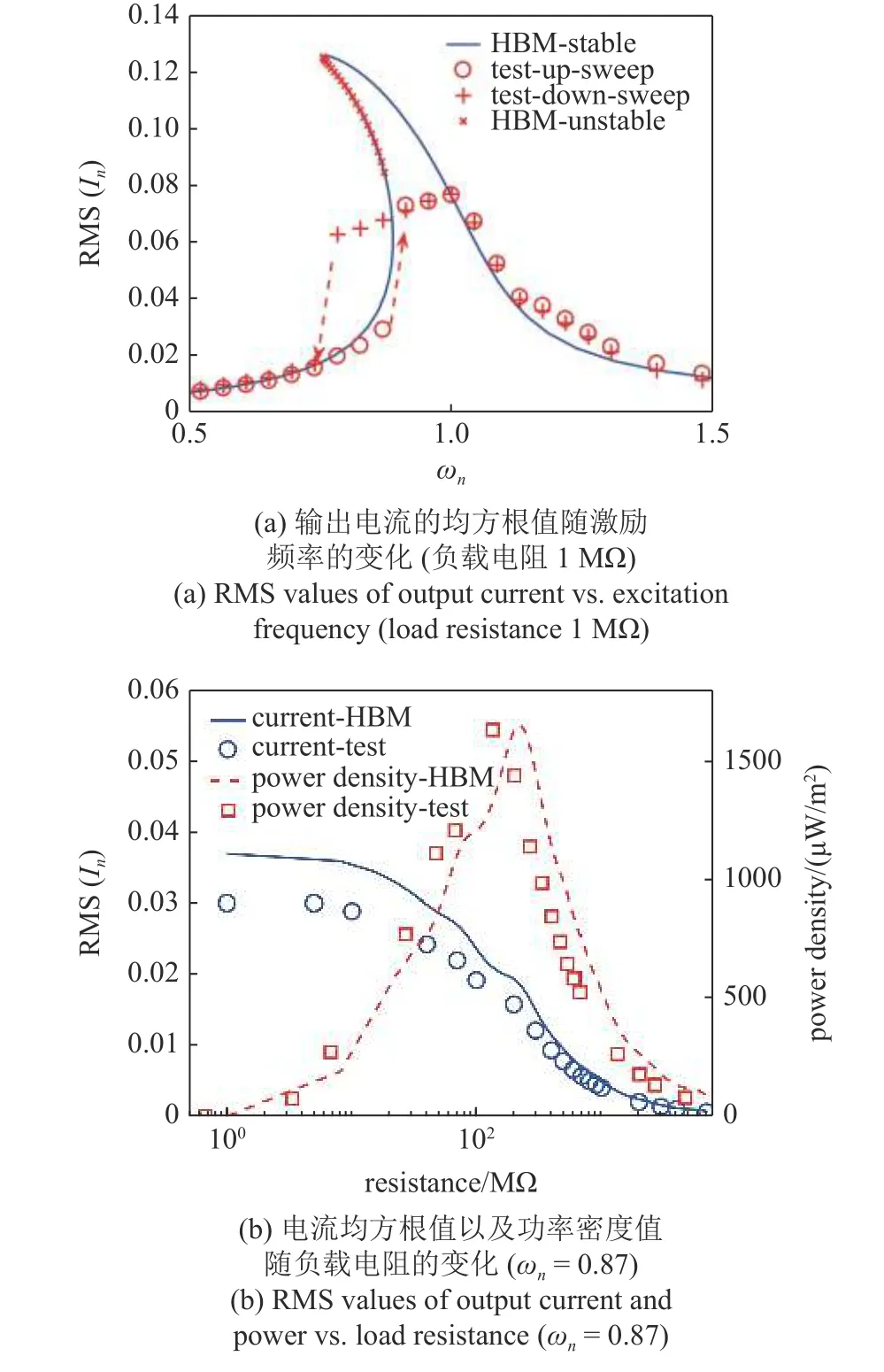
图10 HBM 结果与试验结果的对比Fig.10 Comparison of HBM results with test results

3.3 与线性模型的对比

图11 对比了考虑非线性效应与否对单摆摆动角的影响.当ωn远离系统固有频率时(ωn≪ 1 或ωn≫ 1),考虑非线性效应与否对结果影响不大.从式(6)来看,相当于θ3的影响可忽略不计.当ωn处于1 附近时,由于振幅较大,此时θ3的影响不可忽略.根据式(6),非线性的作用使得系统刚度被削弱,表现为“软特性”.因此,曲线峰值向左偏移,因非线性软特性效应也使得最大摆角显著增加.未考虑非线性效应时,摆角曲线的峰值以ωn=1 对称.选取ωn=0.92 (case 1)和ωn=1.04 (case 2)两种情况,对比了摆角稳态响应及其频谱,如图12(a)和图12(b)所示.对于情况1,考虑非线性效应,使得稳态摆角幅值大于未考虑非线性效应的情况,且频谱中激励频率的3 倍频(3ωn)较为明显;对于情况2,则刚好与情况1 相反,且频谱中的3ωn幅值相对较低.图13(a)中给出了非线性效应对P-TENG 输出电流的影响.与摆动角的结果类似,在ωn处于1 附近时,非线性效应对P-TENG 的输出有显著影响.引入两个指标:工作带宽Bw和最大输出电流Imax,如图13(a)所示,用于衡量P-TENG 输出特性.图13(b)分别考察了非线性效应对两个指标的影响.考虑非线性效应,对最大输出电流的结果影响不大,但是模型预估的工作带宽显著增加,相对增量83%.结果表明,本文提出的模型能够有效避免现有模型对工作带宽的低估问题,显著提升模型对P-TENG 输出性能估计的准确性.

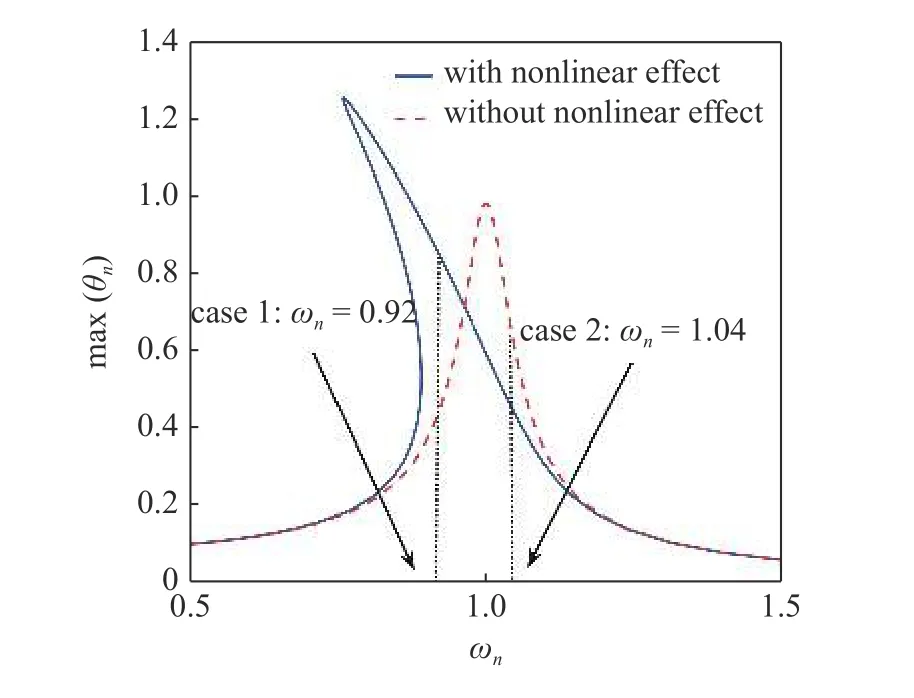
图11 考虑非线性效应与否对摆动角位移的影响Fig.11 Comparison of the influence of the consideration of the nonlinear effect for pendulum angle response curves

图13 非线性效应对P-TENG 输出特性的影响Fig.13 Comparison of the influence of the consideration of the nonlinear effect

4 分析与讨论

基于本文提出的考虑非线性效应的机电耦合模型,研究不同设计参数对P-TENG 输出特性的影响.这些参数包括: 激励幅值an、阻尼比ζ、间隙长度δ和电极夹角α.当激励幅值an由0.003 增加至0.005 时,如图14 所示,P-TENG 输出电流曲线的峰值所对应的频率范围显著扩大,且最大值也有所增加.增加激励幅值,有助于提升P-TENG 的输出表现.从图15 的定量变化曲线可知,工作带宽Bw随激励幅值以指数形式增加.采用幂函数进行拟合,幂指数为3.16,系数约为5.58×106.最大输出电流Imax则与激励幅值呈现线性正比关系,比例系数约为25.01.

如图16 所示,当阻尼比ζ由0.04 增加至0.07 时,P-TENG 输出电流曲线的峰值所对应的频率范围变窄,且最大值也有所降低.为了维持P-TENG的输出表现,应尽可能减小系统阻尼.从图17 的定量变化曲线可知,工作带宽Bw和最大输出电流Imax均随阻尼比以幂指数形式降低.拟合的结果为:对于工作带宽,幂指数为-3.1,系数约为9.63×10-6;对于最大输出电流,幂指数为-0.93,系数约为6.3×10-3.

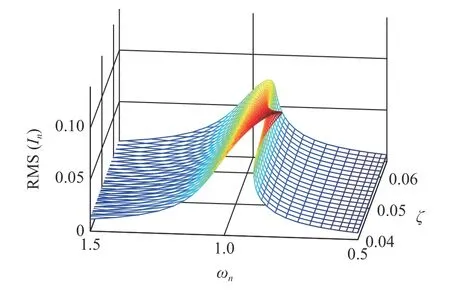
图16 阻尼比对输出电流均方根值影响的瀑布图Fig.16 Waterfall map for the effect of damping ratio an on the output performance of the P-TENG

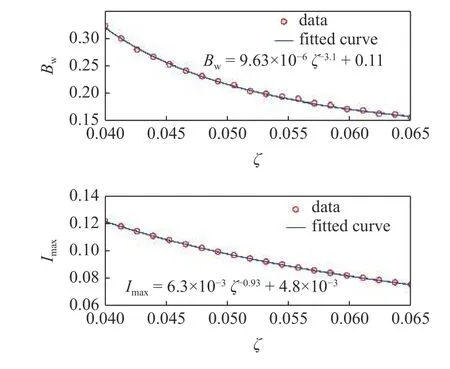
图17 工作带宽和最大电流随阻尼比变化曲线及拟合结果Fig.17 Variation curves of operation bandwidth and maximum output current with damping ratio and fitting results

当结构参数(间隙长度δ和电极夹角α)变化时,P-TENG 等效电容随摆角的曲线发生变化,由此带来式(1)和式(2)中的拟合系数值也随之变化.需要分别确定不同结构参数时相应的拟合系数值(即a1,a2,a3和a4),以用于机电耦合模型的数值分析.如图18所示,当间隙长度δ由0.2 mm 增加至1.5 mm 时,PTENG 输出电流曲线的最大值和工作带宽均有所降低.分别采用幂指数函数拟合工作带宽、最大输出电流与间隙长度δ的关系,如图19 所示,可得幂指数分别为-0.07 和-0.09,系数分别为0.21 和0.12.为了保持P-TENG 的输出表现,应尽量降低间隙长度.但是,间隙过小,易使单摆与电极表面的摩擦力增加,导致加速磨损问题.在实际设计时,需综合考虑间隙长度和摩擦力幅值,以使P-TENG 输出表现处于较优状态.

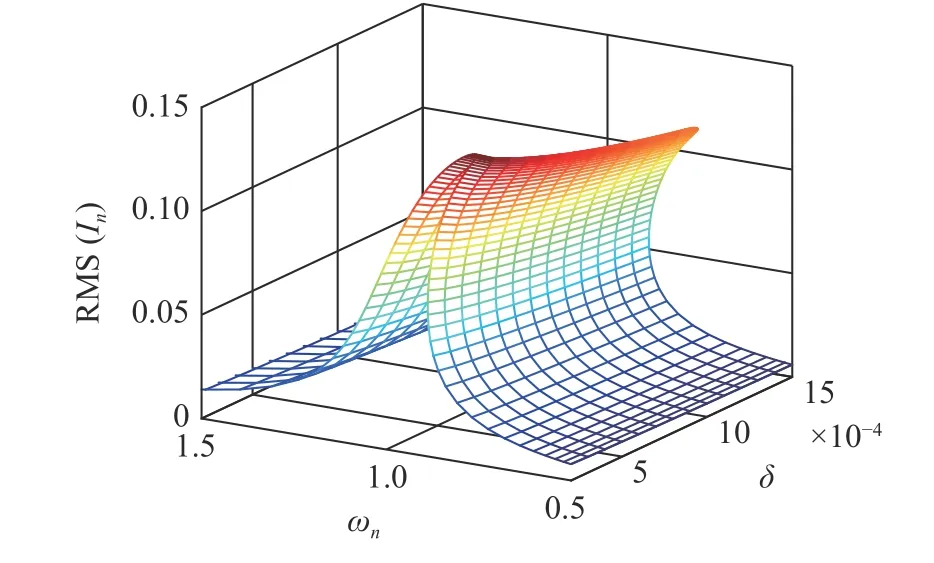
图18 间隙长度对输出电流均方根值影响的瀑布图Fig.18 Waterfall map for the effect of gap length an on the output performance of the P-TENG

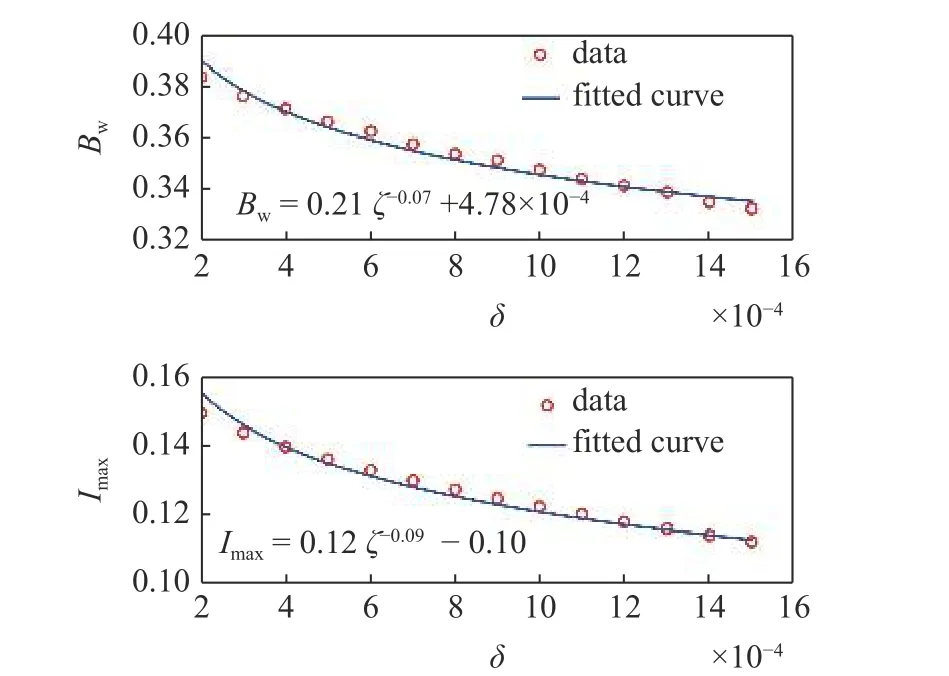
图19 工作带宽和最大电流随间隙长度变化曲线及拟合结果Fig.19 Variation curves of operation bandwidth and maximum output current with gap length and fitting results

当电极夹角α由10°增加至70°时,如图20 所示,P-TENG 最大输出电流值持续下降,工作频带也有所收窄.从图21 的拟合结果可以看出,工作带宽、最大输出电流与电极夹角均呈现为采用线性反比关系.比例系数分别为-0.01 和-2.6×10-3.应尽量减小电极夹角,以提升P-TENG 的输出表现.

图20 电极夹角对输出电流均方根值影响的瀑布图Fig.20 Waterfall map for the effect of electrode angle an on the output performance of the P-TENG

上述分析基于本文提出的考虑非线性效应的机电耦合模型,定量研究了不同设计参数对P-TENG输出特性的影响.通过参数影响分析得到的拟合系数,可作为P-TENG 输出性能设计的依据.

5 结论

本文提出了考虑单摆摆角非线性变化的机电耦合模型,并利用谐波平衡法解析求解P-TENG 的动态输出特性.采用数值积分和动态测试两种手段,验证了谐波平衡结果的准确性.本文得出结论如下.

(1)考虑非线性效应,模型预估的工作带宽显著增加,相对增量83%.结果表明: 本文提出的模型能够有效避免现有模型对工作带宽的低估问题,显著提升模型对P-TENG 输出性能估计的准确性.

(2)增加激励幅值、降低系统阻尼或减小电极夹角,均有助于提升P-TENG 的输出表现.在实际设计时,需综合考虑间隙长度和摩擦力幅值,以使PTENG 输出表现处于较优状态.

(3)提出了多种拟合模型用于表征设计参数与输出性能的关系,并给出相关系数值,可作为PTENG 输出性能设计的依据.