基于光斑投影3D-DIC 的动态液面波高场测量方法研究1)
王 凯 李得睿 向 升 程 斌
(上海交通大学船舶海洋与建筑工程学院,上海 200240)
引言
流体的形状是其力学特征的重要表征,液体表面波高场及其面型的精确测量是流体力学、晃荡动力学、凝聚态物理、波动理论和生物力学等领域科学研究的重要手段和迫切需求[1-5].然而,由于液体通常具有透明度高、流动性强和表面镜面反射强等特点,对其表面动态波高场进行高精度测量及重建一直是个难题.
传统的液面高度测量方法为传感器测量法,包括电容式传感器、光纤传感器、超声波传感器和线性传感器等[6].此类传统方法多用于燃油箱中油液的液位高度的粗略测量,难以对流动的动态液面进行高精度的全场测量和三维重建,因此应用该方法对晃动下的大形变液面进行液面高度测量时会导致测量误差大幅增加.
三维面型测量的光学测量方法具有非接触、测速快和精度高等优点,广泛应用于实物仿形、工业制造与检测和生物医学等领域[7-10].近年来,随着光学测量技术在固体形变测量中的应用,大量国内外学者尝试应用各类光学测量原理实现对液体表面面型的高精度全场测量.目前主流的光学测量方法有立体视觉匹配法、条纹分析法和特征布置法[11].关于立体视觉匹配法郑坤等[12]提出一种基于高斯金字塔图像的改进Harris 特征点检测算法,提高了海面特征点检测的准确度和三维重建的精度,实现了海浪的三维信息重建,为海洋防灾减灾提供了监测方法;梁海香[13]为增加水面的表面特征,向水面投影网格图像,应用最小二乘法将波面三维坐标拟合为三维曲面,获得波浪的等高线图.在利用条纹分析法的液面重建测量研究中,赵文杰等[14]为获取磁场中气液界面的特性参数,提出基于镜面反射成像与结构照明相结合的方法,根据图像映射和条纹灰度矩阵提取条纹图的相位差实现对磁致液面的三维重建;管文洁等[15]采用微小二氧化钛粉末增强水表面的成像能力,以离焦投影技术对黑白二值条纹进行处理获取高速投影的正弦条纹,基于傅里叶变换轮廓术实现了对竖直壁面下降液膜的表面形貌重建.关于特征布置法,Murase[16-17]通过在装有透明液体的容器底部放置特定图案并垂直于透明液体表面放置单目相机拍摄池底图像,使用光流法分析折射后的图像,实现透明液体表面形状重建.邹玲等[18]使用多台相机对透明液体底部的黑白棋盘格拍摄,使用Harris 角点检测法从棋盘格图像中获得动态液面的特征信息,结合标定获得的相机内外参数实现了水面波高场计算并重建了多种工况下的水面三维重建模型.上述3 类方法测量液面的三维形貌的精度普遍较低,一般为毫米级,且均有一定的局限性.立体视觉匹配法一般难以直接对透明的液体进行特征匹配,同时水介质的透光和反光等效应也会增加波浪双目图像的差异性,导致波浪图像匹配精度较低,影响测量精度;条纹分析法离散地求出条纹中心部分点的深度信息,再使用插值方法近似求解出其余点来还原液面整体的三维信息,测量复杂的液体表面时精度低;特征布置法在对动态液面的进行测量时,液面大幅变形将严重增加容器底部的图像的光学畸变,难以对较大扰动的动态液面进行有效测量.
数字图像相关(digital image correlation,DIC)方法作为一个高精度和高鲁棒性的光测技术手段已广泛应用于各类固体的变形和位移测量,若能较好解决液体表面人工制斑的难题,便有希望实现动态液面波高场的亚像素级精度的测量和重建.Krenn 等[19]基于光在两个透明流体界面的折射效应,通过使用数字图像相关算法测量液膜下方随机图案的折射图像位移场,间接测量液膜表面斜率在干燥进程中的变化,该方法重建的液体表面斜率与轮廓仪测量值的最大偏差为25%.Chien 等[20]向待测液体中加入白色染料并投影散斑,在二维数字图像相关(2D-DIC)方法的基础上,通过“相机组-液面”的几何关系及坐标变换推导实现液面三维位移的测量,该方法对相机放置的相对位置的精度要求很高.试验结果表明,方法的测量相对误差在3%以内,可控重复性误差在4%以内.Liu 等[21]使用单目相机向池底贴有散斑图像的水面拍摄,结合多向牛顿迭代算法和散斑相关算法,通过散斑图像的面内位移矢量场计算液体表面的动态变形场.结果表明在大多数区域,试验结果和真实数据之间的差异在5%以内,但方法受限于液体折射产生的大量畸变,难以对高频扰动作用下的液面形态进行测量重建.Huang 等[22]提出双层彩色数字图像相关方法,在容器底板放置红、蓝两层重叠散斑图像,建立液面高度与下层双层颜色散斑虚畸变的内联关系,实现了单目相机对液面的三维重建,作者仅对透明的三棱柱和凸透镜进行了三维重建的误差分析,相对误差分别为2.09% 和4.79%.
上述基于数字相关方法的液面测量研究中,大多基于特征布置法,在面向静态或准静态液膜或透明立体时具有较高的精度,但难以对较大扰动的高频动态液面进行有效测量,且大多研究缺少对动态液面测量的精度验证.
针对以上光学测量方法对动态液面三维测量存在的精度低、效率低和抗干扰能力差等缺陷,本文基于光斑投影与双目视觉原理,通过DIC 算法开发,提出一种基于光斑投影三维数字图像相关(3Ddigital image correlation,3D-DIC)的高精度动态液面波高场测量方法.通过建立几何光学模型进行模拟动态液面的测量试验,搭建测量系统进行真实液面测量试验,并对该方法的可行性、准确性和有效性进行了验证和分析.
1 光斑投影3D-DIC 测量方法
1.1 光斑投影
在应用DIC 进行物体表面全局形变计算时首先需要精确追踪物体变形前后的表面纹理变化所携带的灰度变化信息,进而采用包括零均值归一化最小平方距离 (zero-mean normalized sum of squared difference,ZNSSD)函数或零均值归一化互相关(zero-mean normalized cross correlation,ZNCC)函数等主流相关度函数进行互相关匹配计算,最终获得物体表面的全场形变信息,该算法现已广泛应用于各领域固体对象表面形变的测量[23-27].然而区别于固体的物理本质特性,大多数液体具备较强的流动性,即在受任何微小的剪切力作用下都能产生连续变形.针对动态扰动下液体表面波高场测量场景,提出了一种光斑投影方法以将DIC 方法由常规的固体形变测量引入到液体形变测量.本方法通过使用墨水染色方式对液体进行去透明化处理,再以具备高亮度、高分辨率和高对比度的投影设备向已染色的液面投影散斑,如图1 所示.该方法通过光学投影的方式,将散斑纹理直接附着于液体表面,待测液体与散斑纹理之间并不需要形成物理上的黏附,实现了一种便捷的液体表面散斑制备方法.相较于其他液体表面散斑附着方法,该光斑投影方法具有非接触、操作便捷、成像清晰的特点,尤其适合应用于动态扰动下液面波高场的3D-DIC 测量.

图1 液面染色与光斑投影Fig.1 Liquid dyeing and optical speckle projection
1.2 DIC 基本原理
DIC 计算的基本策略是通过对一个固定像素区域内的图像数据在时间域上的连续变化进行分析,实现亚像素级别的高精度位移及形变测量.如图2所示,DIC 算法首先以测量对象上某一目标测点作为几何中心建立一个参考像素子区,通过整像素搜索算法对下一帧图像进行粗匹配,找到该像素子区的整像素形变结果,进一步将其作为迭代初值,代入DIC 亚像素迭代算法计算中,进而基于形函数进行亚像素匹配运算,最终实现高精度形变测量.DIC 主流的亚像素算法为前向累加牛顿拉弗森算法 (forwardadditive Newton-Raphson,FA-NR)[28]以及反向组合高斯牛顿算法(inverse-compositional Guass-Newton,IC-GN)[29-30].
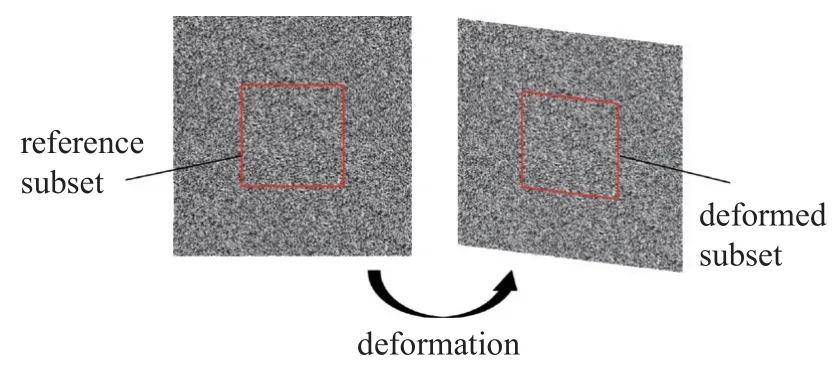
图2 DIC 测量示意图Fig.2 Schematic diagram of DIC measurement
待测物实际图像的变形子区可能存在非常复杂的变形,包括刚体平移、旋转、拉伸、剪切或更复杂的非均匀变形等.在应用DIC 对待测物表面进行实际测量时,可针对待测物表面各异的变形形式采用不同阶的形函数对其变形子区进行最优的形状拟合.通常形函数的阶数越高,其对变形的拟合能力越强,0 阶形状函数允许子集进行刚体平移,1 阶形状函数可以表示子集的仿射变换,即允许平移、缩放、旋转和剪切的组合[31-32].2 阶形函数不仅可以表示线性变形,同时还能够表示更为复杂的同向非线性变形,如弯曲和局部扭曲等.考虑一个二维变形情形,参考图像子区中的每个点(x,y)映射到变形后图像中对应变形子区中表示为(x',y')的数学表达式为
式中,U和V分别表示子集中每个点的横向和纵向位移分量,在子区中点(x0,y0)附近,以该点为中心进行2 阶泰勒级数展开来近似U和V,即2 阶形函数表示为
式中,U和V的各阶位移梯度的位移分量构成了共12 个映射参数.如图3 所示,相较于0 阶形函数和1 阶形函数,2 阶形函数通过12 个映射参数的不同组合可更精确地拟合更加复杂的非均匀变形.
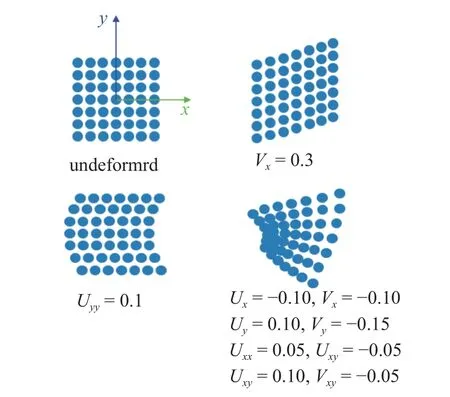
图3 形函数与映射参数Fig.3 Shape functions and mapping parameters
在对固体双目图像进行立体匹配时,一般情况下至多采用8 个映射参数的透视变换形函数,但在本文动态液面波高场测量中,DIC 测量对象为高频扰动下的液体表面,其较之固体表面具明显的流动性,且其面型的非均匀形变更为复杂.因此,本文采用具有12 个映射参数且基于2 阶形函数的IC-GN算法对液面进行亚像素级形变测量,进而为双目三维重建提供高精度的二维测量原始数据.
1.3 双目视觉与3D-DIC
3 D-DIC 是2D-DIC 基于双目视觉原理的直接三维拓展,涉及双目相机精确标定、立体匹配和形函数选择等与立体测量相关的内容.
本文将一对双目相机组垂直架设于液体表面上方,实时采集动态液面光斑图像,进而基于3DDIC 测量液面的全场三维波高场.3D-DIC 的核心算法与2D-DIC 完全相同,基于双目视觉原理实现物体表面三维形变场测量,且相较于单目视觉三维测量(PnP 原理),双目视觉可直接测量得到物体的三维形变信息[33],具有更好的可靠度与适用性.双目视觉进行三维信息测量的数学模型如图4 所示[34-35].
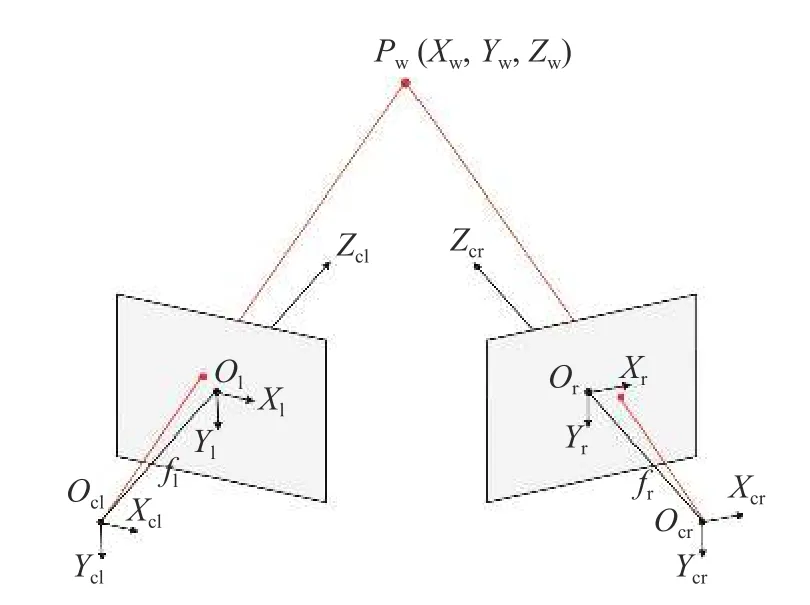
图4 双目视觉数学模型Fig.4 Mathematical model of binocular vision
在图4 所示的双目相机的相交视场中,设某一物点Pw在世界坐标系O-XwYwZw中的三维坐标为(Xw,Yw,Zw).设左、右相机的焦距分别为fl和fr,左、右相机的相机光心分别为Ocl和Ocr,左、右相机的靶面几何中心分别为Ol和Or;设世界坐标系与左相机坐标系Ocl-XclYclZcl重合,右相机坐标系为Ocr-XcrYcrZcr;左相机和右相机的图像物理坐标系分别为Ol-XlYl和Or-XrYr.基于小孔成像原理的线性成像模型中的相似三角形关系,物点Pw在各相机坐标系下的坐标至对应图像物理坐标系下齐次坐标的转换关系为
式中,sl和sr分别为左、右相机成像模型中的比例因子.进一步,左相机坐标系可通过旋转和刚体平移变换转换为右相机坐标系,其数学表达为
式中,R为左相机坐标系至右相机坐标系的旋转矩阵,T为左相机坐标系至右相机坐标系的平移向量.将式(4)代入式(3)并求解可解得世界坐标系下物点Pw的三维坐标(Xw,Yw,Zw)为
由式(5)可知,若一对双目系统的左相机焦距和右相机焦距(相机内参数)已知,旋转矩阵和平移向量(相机外参数)也已知,则可通过左、右两幅图像上对应点的坐标求得物点在世界坐标系下的三维坐标.本文方法基于张正友标定法实现双目相机标定[36],该标定法需要的前置数据为标定板的角点坐标.实际波高测试中,由于液面波动导致的光斑噪声污染严重,采用传统标定板及对应的识别算法进行波高原位标定时,容易将光斑噪声误识别为标定板角点,导致标定困难.为此,自主研发了交比不变标定板[37],如图5 所示.利用该标定板的5 个交比标志点求解单应性矩阵,实现了快速、高鲁棒性和高精度的标定板识别和更精确的内外参数求解,大幅减小了环境噪声对图像标定的干扰.

图5 交比不变标定板Fig.5 Cross-ratio invariance calibration plate
1.4 方法步骤流程
基于光斑投影3D-DIC 的动态液面波高场测量系统的组成如图6 所示,主要设备包括双目相机、投影仪、同步触发设备和计算机.首先采用染色等方式对液体进行去透明化处理,降低水体对光的透射,并在液面的法平面内架设投影仪,向水面垂直投射随机分布的光斑.同时在液面上布置双目相机组,调整相机组位置及镜头光学参数,直至获得适宜的视场及清晰的液面光斑图像,并固定相机组的位置及光学参数.进一步使用标定板对双目相机进行内外参标定并保存标定数据.为实现处于高频运动状态下液面的精确波高场测量,需确保双目相机在拍摄时,左、右相机实现严格地同步采样,因此左、右相机均需连接至一个可使双目相机同步采样的硬触发设备,实现双目相机采样时间差在10 ns 以内.按实际测量需求,在触发设备上设置拍摄帧数和采样频率,同步拍摄动态液面的光斑图像,最后基于3DDIC 算法实现各个时刻液面三维波高场的高精度重建.
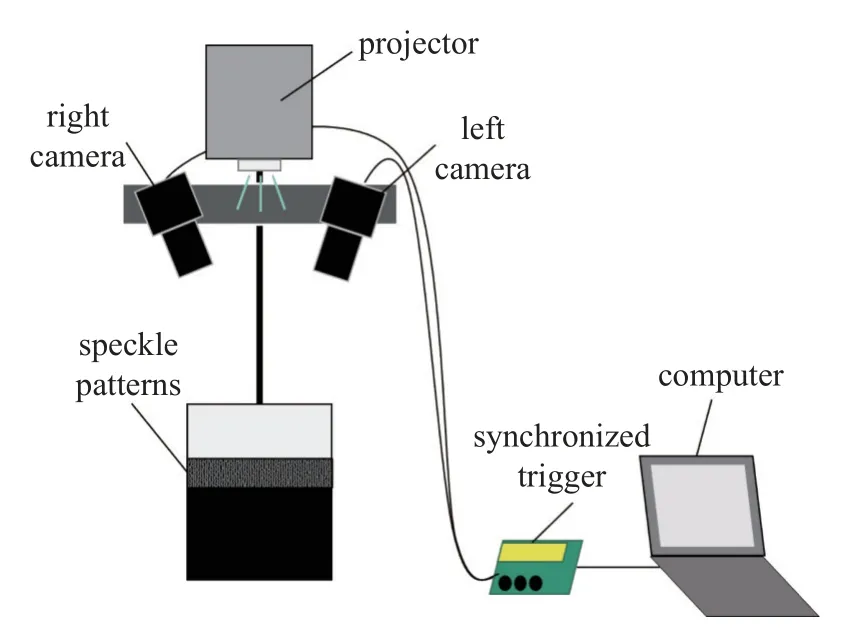
图6 测量系统Fig.6 Measurement system
2 动态液面模拟测量试验
2.1 动态液面模拟成像方法
为了验证以光斑投影3D-DIC 的动态液面波高场测量方法的准确性,本文基于相机小孔成像的真实光路建立了一个几何光学模型,该模型能够模拟三维空间任意视角下的液面散斑双目成像.图7 为该模拟方法的几何光路模型,该模型通过从CMOS芯片某像元处向光心发射一道光线,进一步通过特定的光路算法及波高方程,计算得到该光线与液面波高处交点在世界坐标系下的三维坐标,最后基于图像插值算法获得液面波高散斑图像的真实投影成像结果.

图7 几何光路模型Fig.7 Geometric optics model
图7 中,首先在平静液面上建立世界坐标系OXwYwZw,在垂直于原始平静液面的法平面内定义一对已知内部参数及外部参数的双目相机.在“相机组-液面”的特定几何关系下,左相机与右相机的光心在世界坐标系可分别确定为同时,在像元尺寸确定的情况下,左相机与右相机的CMOS 感光芯片的某一个感光点在世界坐标系中的坐标分别也对应地确定为设双目相机的任一感光点所成的像对应于平静液面上的光斑在世界坐标系中的坐标分别为和(),根据小孔成像的光路模型,求解其世界坐标为
遍历求解感光芯片每个感光点对应的液面处光斑的世界坐标,进一步基于解得的液面光斑的世界坐标通过双3 次样条插值算法生成双目相机的液面光斑图像.进一步,向作为平静液光斑的散斑图像输入机械波,设某时刻液面方程可表示为
式中,(xw,yw,zw)表示液面上某个光斑的世界坐标,(xc,yc)为输入机械波的波源坐标.以相同方法求解根据小孔成像原理双目相机感光点对应于动态液面上的光斑的世界坐标,进而通过3 次样条插值生成双目相机的液面光斑图像,如图8 所示.

图8 模拟双目图像Fig.8 Simulated binocular images
进一步对液面散斑的密集目标点云进行立体匹配,为解决传统极线搜索式匹配算法耗时长、鲁棒性低的缺点,首先使用SIFT 算法对双目图像的同名种子点进行粗匹配,再基于2 阶形函数对粗匹配结果进行亚像素迭代,实现更高效的立体匹配并进行后续DIC 运算.
2.2 模拟动态液面测量结果
基于上述模拟动态液面图像模拟方法,运用本文方法对模拟的波高场进行全场三维测量,并验证其精确性,模拟采用的双目相机的内部参数及输入到液面波源的简谐波的详细参数为: 双目相机焦距8.0 mm,像元尺寸3.45 μm×3.45 μm,简谐波振幅6.0 mm,波长100.0 mm.
在上述参数下生成双目相机的模拟波面光斑图像,选择正方形区域进行模拟液面波高场的全场三维测量,模拟液面的三维重建结果如图9 所示.可以看出,液面的三维重建结果与模拟的波高场形状吻合,输入到液面的简谐波振幅和波长等信息在重建云图中得到了较好的再现.
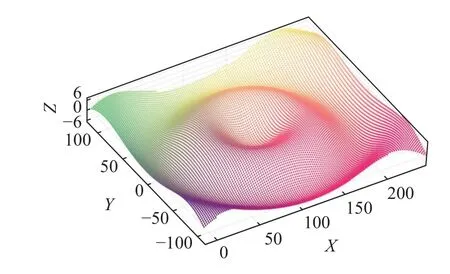
图9 模拟液面三维重建结果Fig.9 3D reconstruction result of simulated liquid surface
对模拟动态液的三维测量结果进行全局精度分析.首先对模拟动态液的三维测量结果进行全局精度分析,通过本文方法计算得到的动态液面的三维点云后,将计得点云垂直于高度变化方向的内坐标(x,y)代回式(8)中,计算得该点波高的理论值,进一步求解全部点云对应的波高的理论值与测量值误差的均方根(root mean square,RMS)为0.004 mm.为验证该方法局部的测量精度,设进一步在所重建点云的纵坐标y的1/2,1/4 和1/8 处做切面并求取该切面内液面波高测量值与理论值的误差,将切面内液面高度的测量值与理论值绘制为散点图,如图10所示.图10 所示3 个切面液面高度的DIC 测量值与理论值吻合程度好,计算得其测量的RMS 值分别为0.005,0.003 和0.003 mm.
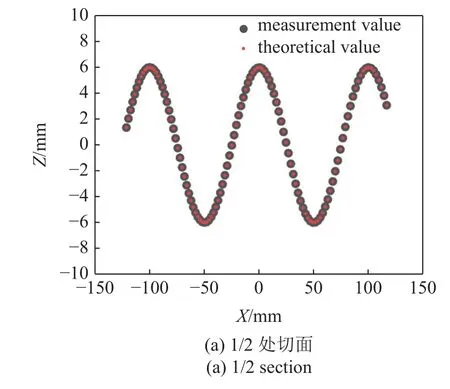
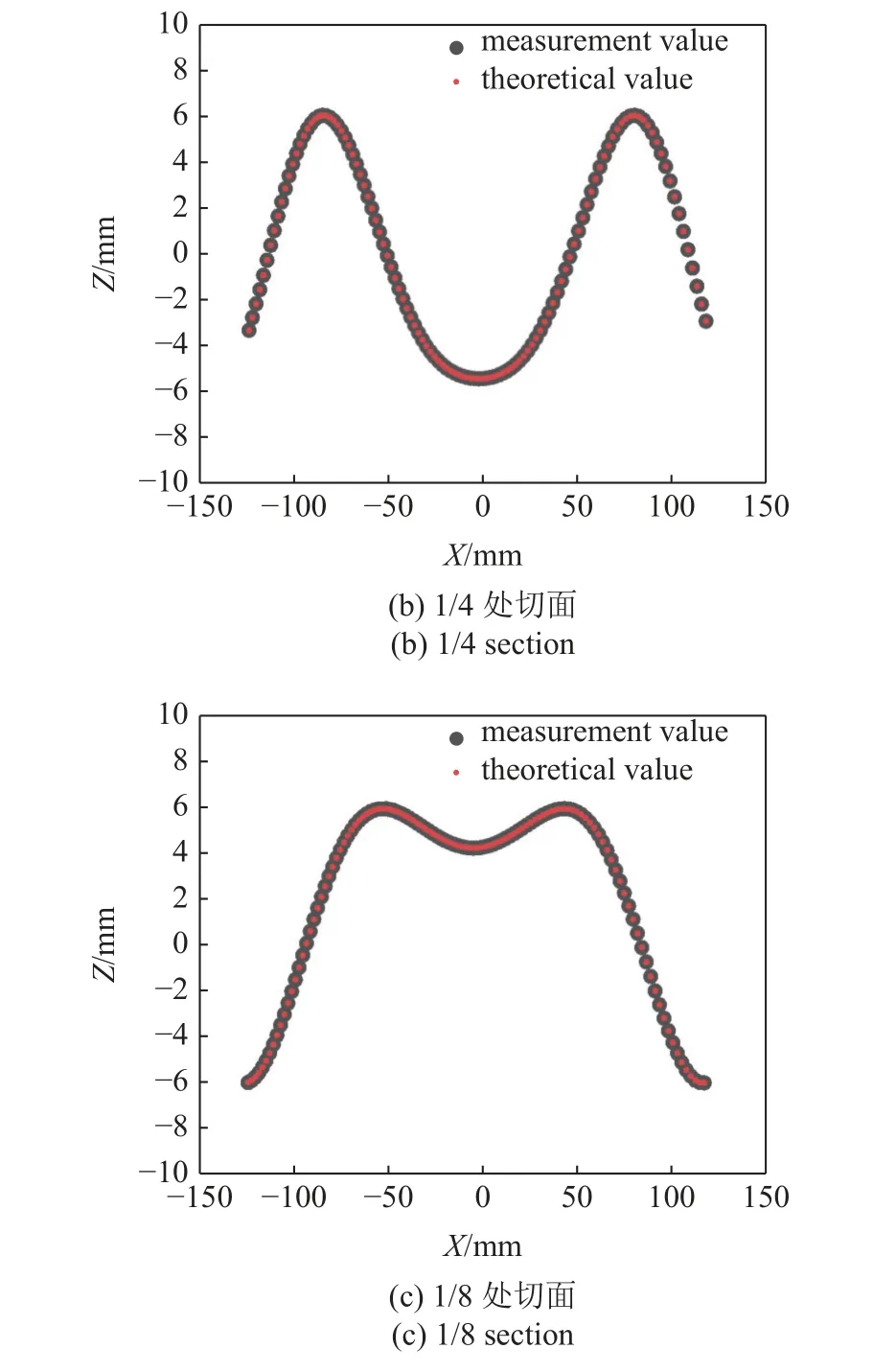
图10 局部测量结果Fig.10 Local measurement result
3 动态液面真实测量试验
3.1 试验装置
通过模拟试验验证本文方法的准确性后,进一步搭建了光斑投影的液面波高场测量试验系统,从而对该测量方法进行可行性及准确性验证.试验装置组成如图11 所示.试验装置由上至下为投影仪、双目CMOS 工业相机、装有待测液体的透明容器、容器侧壁的单目CMOS 工业相机、相机同步硬触发装置和计算机.双目相机采用迈德威视MVSUA501 GM 工业相机,分辨率为2448×2048,距离液面约50 cm 拍摄光斑图像.容器侧壁的单目相机采用迈德威视MV-SUC401 M-T 工业相机,分辨率为2048×2048,其光轴垂直于容器侧壁,距离侧壁约20 cm 对液面边界线进行拍摄,将其测量得到的液面边界线结果与液面全场3D-DIC 测量结果进行对比分析.3 台相机均配备16 mm 定焦镜头.3 台工业相机均与硬触发装置连接,以确保拍摄全过程中3 台相机的采用时间差小于10 ns.液体装于精确定制的立方体容器,容器内壁尺寸为150 mm,容器侧壁平整对光线的折射忽略不计,容器侧壁竖直放置刻度尺,用于将侧壁液面边界线的2D-DIC 结果量化为实际的物理尺寸.该试验装置布置可表达动态液面波高场测量的真实工作状态,容器侧壁处的单目相机是为了验证本文3D-DIC 方法的精度所用,在实际的测量应用中无需安装此单目相机.
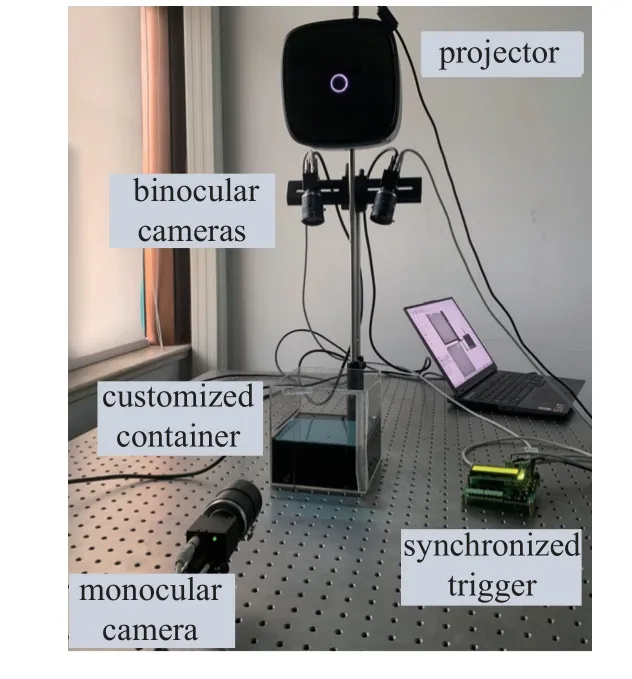
图11 试验装置组成Fig.11 Experimental set up
3.2 精度验证试验
3.2.1 静态液面抬升试验
试验开始前,使用随机散斑生成软件Glare 结合待测液面尺寸生成适宜密度和粒径大小的散斑图像,使用投影仪投射光斑到染色处理后的静止液面,对投影距离和投影焦距进行调整,直至液面上呈现清晰分明的光斑图像.
调整双目相机组左、右相机的间距和夹角,直至两相机均获得清晰完整的液面光斑图像,使得待测液面处于双目相机的相交视场下并且左、右相机的图像具有必要的相似性.固定左、右相机的相对位置并在试验过程中保持不变,使用标定板对双目相机进行标定并保存相应的内、外参数数据.
液面静止时,拍摄初始状态下的液面光斑图像,随后使用量杯分8 次量取等量体积V=55 mL 的水,使液面逐次抬升同一高度,每次加液后等待液面完全静止,再以双目相机拍摄该液面的静态液面光斑图像.本试验静态液面抬升高度的级差为
3.2.2 动态液面波高场测量试验
使用与静态抬升试验相同的方法进行双目相机的安装和标定.特别地,需要调整容器侧壁的单目相机位置,使得相机垂直于容器侧壁拍摄,相机光心与液面边界线近似位于同一水平高度上.微调光斑投影仪,使得容器侧壁正对单目相机的液面边界线上出现由投影光线产生的微小光点,用于反映液面边界线的高度变化.测量过程中选取液面相机相交视场以外的某位置作为波源,使用玻璃棒手动施加上下往复的激振力,产生高频的液面动态变化,并生成不规则的液面波浪.设置3 台相机以30 Hz 同步拍摄液面光斑及容器侧壁的波高图像,如图12 所示.

图12 3 台相机的图像Fig.12 Images shot by three cameras
3.3 试验测量结果分析
3.3.1 静态液面抬升测量结果
试验选取液体表面双目相机公共感兴趣区域(region of interest,ROI)进行计算分析,ROI 内共计生成n=13 352 个目标点,设每个计算点垂直于液面方向坐标为zi,以全部计算点zi的平均值作为此次液面高度.设初始静态液面高度为h0=0 mm,精确量取液体加入容器使液面逐级抬升,记第I次加水后液面高度测量值为hI,第I次液面抬升测量值为记为ΔhI,记该次液面抬升测量值与液面抬升实际值误差为
将每次液面抬升的测量误差取均方根,试验中静态液面抬升测量的RMS误差计算公式为
进一步计算各级液面全部目标点zi坐标的标准差S记为各级液面的点云离散度,以反映各级液面的平整情况.各级液面静态抬升测量数据的精度验证结果见表1.从表1 可以看出,本文方法对液面静态抬升量的测量精度较高,最大误差限制在0.05 mm以内,且重建液面的离散度小,具有全场有效性.
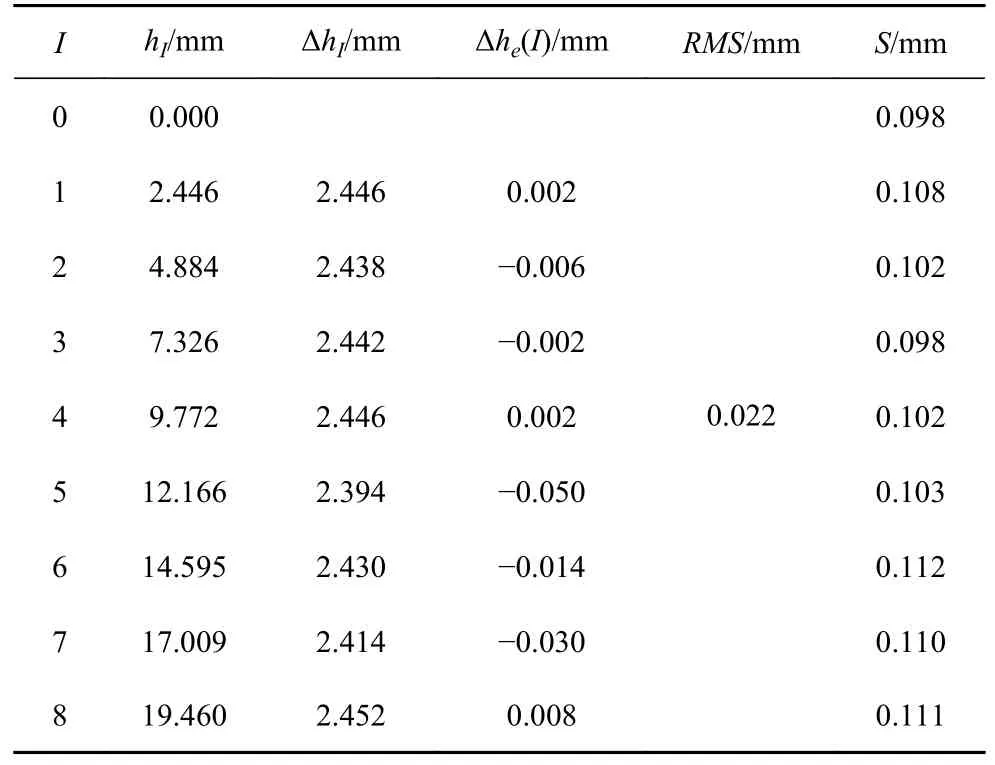
表1 静态液面抬升测量精度验证结果Table 1 Accuracy verification of static liquid level rise
3.3.2 动态液面测量结果
在双目图像中,选取一个60 mm×60 mm 的正方形ROI 计算其三维波高场,该正方形ROI 的一条边与容器侧壁2D-DIC 计算的液面边界线严格重合.通过3D-DIC 后处理计算,测量ROI 的三维液面波高场.为使实验结果更具代表性,以1 s 作为时间间隔,选取相对差异较为明显的典型液面形态进行三维重建.以正方形ROI 的右上角点作为三维坐标系原点,以容器侧壁方向向左作为X轴正方向,以液面抬升方向作为Z轴正方向,建立三维坐标系.该坐标系中t=1,2,3,4 s 时刻液面波高场的三维重建云图如图13 所示.可以看出,波高场重建云图的平顺性良好、形态真实,动态液面的曲率、波纹纹理等关键几何特征在云图中均得到了很好的再现.
图14 为t=1,2,3,4 s 时刻容器侧壁液面边界线的原始拍摄图像,图中红色标记为液面边界线上投影光点的连线,揭示了各时刻容器侧壁液面边界线的线形走势.
将图13 与图14 进行对比分析,可以看出: 图13三维重建结果中液面边界线的升降趋势、升降幅度、曲率变化等几何特性与图14 中的液面边界线形保持了较高的吻合度,证明了该测量方法的准确性.进一步对动态液面测量结果的精度进行更精确的量化验证.使用2D-DIC 测量液面边界线高度变化,通过容器侧壁的标记,在与ROI 边长严格重合的区域选400 个测量点进行测量.
在原始液面边界线上等距地选取400 个测点,以2D-DIC 测量其高度变化,以边界线的2D-DIC 测量结果为基准,计算3D-DIC 的测量误差.以液面边界线延展方向为X,以垂直液面的法线方向为Z,绘制边界线的散点图进行测量结果对比,如图15 所示.
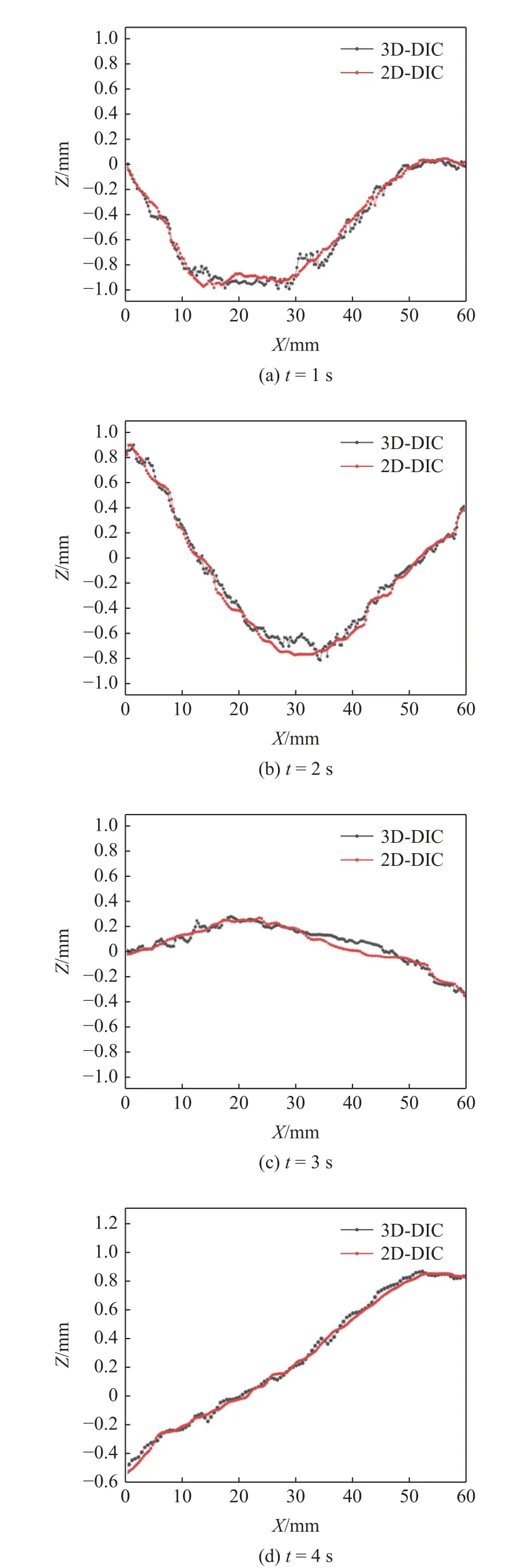
图15 3D-DIC 与2D-DIC 结果对比Fig.15 Results comparison of 3D-DIC and 2D-DIC
图15 表明两种测量方法得到的边界线升降趋势、升降幅度与容器侧壁图像中边界线的线形吻合度高,且两种测量结果的契合程度高.液面张力导致动态液面边界线处散斑畸变相对明显,对DIC 计算造成了一定影响,因此3D-DIC 测量结果所得曲线噪声相对明显.
进一步对3 次测量的结果进行误差分析,计算边界线的3D-DIC 测量值相较于2D-DIC 基准值的最大误差和标准差,误差的计算结果见表2.动态液面测量的误差分析结果表明,其中最大误差为t=2 s 中出现的0.163 mm,相比于Chien 等[20]的DIC 测量方法(最大误差为1.8 mm),应用本文方法进行液面的动态波高场测量具有更高精度.此外,本文算法基于图像后处理开发,在常规算力情况下对容器内液面测量重建的时间约为30 s,可满足多数流体力学实验、晃荡实验等需求,且重建时间可通过提升算力得到进一步缩减.
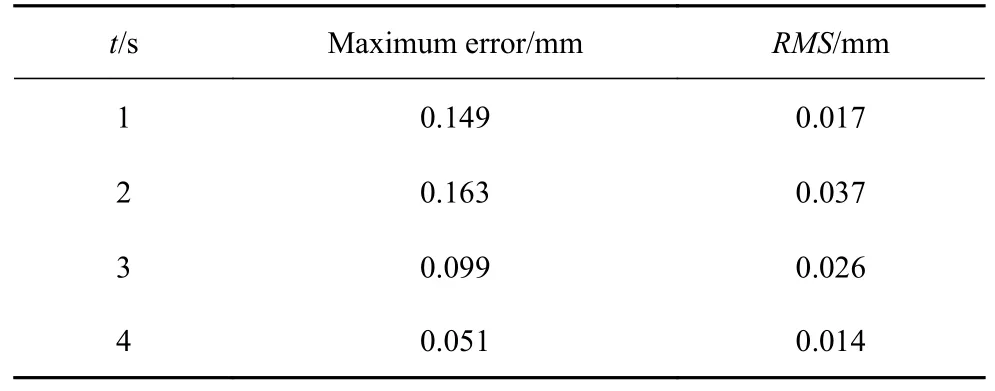
表2 液面边界线的测量误差Table 2 Measurement errors of boundary lines
然而在试验研究的过程中也发现本文方法存在一定的局限性.在使用投影仪对动态液面进行光斑投影时,动态液面上不可避免地会有个别位置将投影光线直接镜面反射至相机光心处,在相机图像中形成纯白色亮斑,对双目图像的匹配造成影响,最终在液面三维重建结果中形成坏点.此外,本方法虽然对液面振动频率具有较好的包容性和适用性,可以实现对常规动态液面的全场测量,但对液面振动幅度大同时波长较短的液面进行测量时,液体表面的光斑投影或将产生过大的畸变,导致双目图像的立体匹配在算法层面失效,影响动态液面三维测量的效果.
4 结论
本文运用光斑投影和双目视觉原理,通过DIC算法开发,提出了基于3D-DIC 的动态液面波高场测量方法.该方法通过对液体进行去透明化处理、光斑投影、双目相机内外参标定、3D-DIC 亚像素测量、点云三维重建等步骤,实现了扰动下动态液面波高场的精确三维数字化重构.
通过开展动态液面模拟测量试验和真实液面测量试验证明了该基于光斑投影的3D-DIC 液面波高场测量方法的精准性与有效性.首先,通过建立该方法的几何光学模型进行了动态液面模拟测量试验,结果表明以本文方法进行动态液面模拟测量试验的全场标准差小于0.004 mm,证明其具有较高的理论精度.进一步搭建试验装置分别开展了静态液面抬升试验和动态液面波高场测量试验,结果表明本方法对液面静态抬升测量的标准差为0.022 mm,对动态液面波高场测量的标准差小于0.037 mm,证明了其应用于真实动态液面波高场测量的有效性.此外,本文方法的空间分辨率非绝对固定值,不同的测试方案具有不同的空间分辨率,这主要取决于双目相机硬件参数、设备空间布置方式等.基于本文所开展试验场景下的硬件条件和设备布置方式,本方法的空间分辨率约为0.001 3 mm/pixel.
虽然本方法目前仍存在一定的局限性,但其与现有的液面全场三维测量方法相比,能够实现大部分复杂扰动下液面波高场的精准测量,在测量精度、测量效率、适用范围和设备成本等方面均具有显著优势,在液面形态检测、流量计量、晃荡动力学试验研究及其他流体力学应用方面具有广泛的应用价值和推广前景.

