基于分数阶导热的热脉冲涂层边裂研究1)
陈少华 陈学军
(北京科技大学应用力学系,北京 100083)
引言
涂层技术广泛应用于工程构件以提高材料的表面性能,例如在航空领域,涂层技术可以有效延长发动机零部件的使用寿命[1].随着服役工况要求的不断提高,热端零部件所承受的温度越来越高,热载荷作用方式越来越复杂.防护涂层承受的热应力一旦超过其强度极限,表面将萌生边缘裂纹.在循环热载荷的作用下,边缘裂纹将继续扩展,导致涂层剥落甚至贯穿至基体内部[2],严重影响涂层的防护性能.基于断裂力学的观点,可采用裂纹尖端的应力强度因子表征热致裂纹扩展驱动力,从而有效预测和评估裂纹的扩展行为.
作为导热理论的本构方程,经典傅里叶定律建立了热流密度与温度梯度之间的线性关系,在处理热致断裂问题上发挥了重要作用[3-4].然而,傅里叶导热方程隐含了无限大热传播速度的假定,适用于热作用时间较长的传热过程.而对于极端传热过程(极高/低温、微时空尺寸等),经典傅里叶导热模型的求解结果会出现偏差.Maurer 等[5]对薄板进行脉冲激光加热后,表面温度比傅里叶定律模型预测的温度高约300 K;Tzou[6]的实验表明,当时间尺度低至ps/Hs 或空间尺度低至μm/nm 时,傅里叶定律模型不再精确;Qiu 等[7]通对金属涂层脉冲激光冲击,实验得到的反射率变化与采用傅里叶定律计算所得的数据相背离.
在对傅里叶导热模型进行修正以描述上述瞬态热传导过程的研究中,考虑时滞效应的C-V (Cattaneo-Vernotte)模型[8]得到了广泛使用.Wang 等[9-11]基于此模型得到了温度场和热应力场的解析解,评估了带裂纹薄板和圆柱体的热冲击性能;Chen 等[12]基于C-V 模型获得了热弹性半无限板裂纹附近的瞬态热应力场,并研究了相应的热致断裂问题.然而,C-V 模型自身也存在局限性,Ahmadikia 等[13]分析了受周期性边界条件的C-V 传热模型,调节热冲击位置等参数,发现弛豫时间对温度场的分布有较大影响,并指出在某些不稳定边界条件下,双曲导热方程可能违背热力学第二定律.
最近,分数阶微积分已成功应用于众多工程领域.大量文献[14-20]表明: 分数阶微分算子定义中的积分项充分体现了系统函数发展的历史依赖性,是描述极端传热现象的有力工具,相比经典傅里叶定律和C-V 导热理论,分数阶导热模型可以更精确地描述极端传热机理,并有效解决奇异性问题.通过对分数阶的阶次α在有效范围内的取值,可以将热扩散形式分为亚扩散(0 <α<1)、正常扩散(α=1)、超扩散(1 <α<2)和弹道扩散(α=2)[21].基于分数阶导热模型,Povstenko 等[22-24]提出准静态非耦合的热弹性理论,研究了各类热载荷下薄板、圆柱体和球体等均质材料的传热机理.此外,通过数值分析解释了亚扩散和超扩散之间的区别,并指出当α=1 时,分数阶导热可以退化为传统傅里叶导热模型.文献[25-28]基于分数阶导热模型分析了预置裂纹均质材料的热致断裂问题,并评估了分数阶导热模型的可靠性.
虽然基于分数阶导热模型的热致断裂问题已有研究,但其研究对象主要集中于均质材料,对涂层-基体复合材料的相关研究相对较少.因此,本文拟基于分数阶导热理论,以热应力强度因子表征边缘裂纹的扩展驱动力,研究热流脉冲作用下涂层边缘裂纹的扩展行为,为涂层的安全服役及可靠性评估提供理论支持.
1 问题描述
考虑涂层-基体系统,涂层厚度为h1,基体厚度为h2,脉冲热流作用于涂层表面,如图1(a)所示.建立笛卡尔坐标系,x轴设定为厚度方向,y轴设定在涂层和基体的界面处.为简单起见,假定两种材料都是均匀的、各向同性的,涂层和基体完好接触,忽略热弹性耦合效应、惯性效应以及温度对力学性能的影响.

图1 涂层-基体模型Fig.1 Coating-substrate model
由于对称性,温度场与y坐标无关,基于Caputo分数阶导热理论[29],建立涂层-基体的温度场控制方程如下
式中,θi=Ti-T0,其中Ti(i=1,2)分别为涂层和基体的温度,T0为初始温度.D为热扩散率,其量纲为m2/sα.下标i=1,2 分别对应涂层和基体,t为时间.α为分数阶阶次,当α=1 时,分数阶导热模型退化为经典傅里叶导热模型.
Caputo 分数阶算子由下式给出
式中,Γ(·)为Gamma 函数,n为(α+1)的整数部分,热流密度与温度的关系满足
式中,q为热流密度,k为导热系数,为R-L(Riemann-Liouville)算子,定义如下[30]
初始条件为
边界条件由下式给出
式中,Q0为冷却热流密度,δ (t)为狄拉克函数.
假设界面完好接触,温度场和热流密度在界面处均连续,即
2 温度场
根据分数阶导数的拉普拉斯积分变换法则[30],对时间t作变换(t→s)
式中,θ∗(x,s)为拉普拉斯变换后的温度场.
考虑初始条件式(5)和式(6),式(1)拉普拉斯积分变换后如下
由式(3)和式(10)得
对式(13)作拉普拉斯积分变换得
式中,为拉普拉斯变换后的热流密度.
同理可得
利用有限余弦积分变换法则[31]对式(12)作空间变量x的变换(x→ξm)得
涂层区域上(-h1≤x≤0)变换如下
将式(7)、式(8)、式(14)和式(15)代入式(17)和式(18)可得
将式(19)和式(20)代入式(16)并整理后得
对式(21)有限余弦逆变换可得
为确定界面处的热流密度q(0,t),采用三角级数求和公式[32],即
利用上述公式对式(22)求和可得
由式(9)可得
联立式(24)、式(25)和式(26)得到
基于Tauberian 近似定理,对热传导求解问题中较小的时间值,拉普拉斯变换中的指数项相比常数项会迅速衰减,因此指数项可以忽略不计,以得到一个更容易数值处理的解析解[33],由此可认为
将式(27)近似处理可得
式(24)和式(25)作同样近似处理,并将式 (8)代入得
最后,利用Mainardi 拉普拉斯积分逆变换法则[34]对式(29)作逆变换得到温度场如下
式中,M(α;z)是Mainardi 函数,即
3 热应力场
涂层表面无面力(见图1(a)),因此 σxx=0.由热弹性平衡方程,可得下式
式中,σ 为应力,E为弹性模量,µ 为泊松比,ε 为应变,p为热膨胀系数.
式中,ε0和 ρ 均为待定常数,可根据热应力自平衡条件确定,即
平面应变条件下,涂层和基体在y方向的热应力为[35]
式中,ε0(t)和 ρ (t)均为与时间t相关的待定参数,表达式见附录A 中的式(A1).
4 热应力强度因子
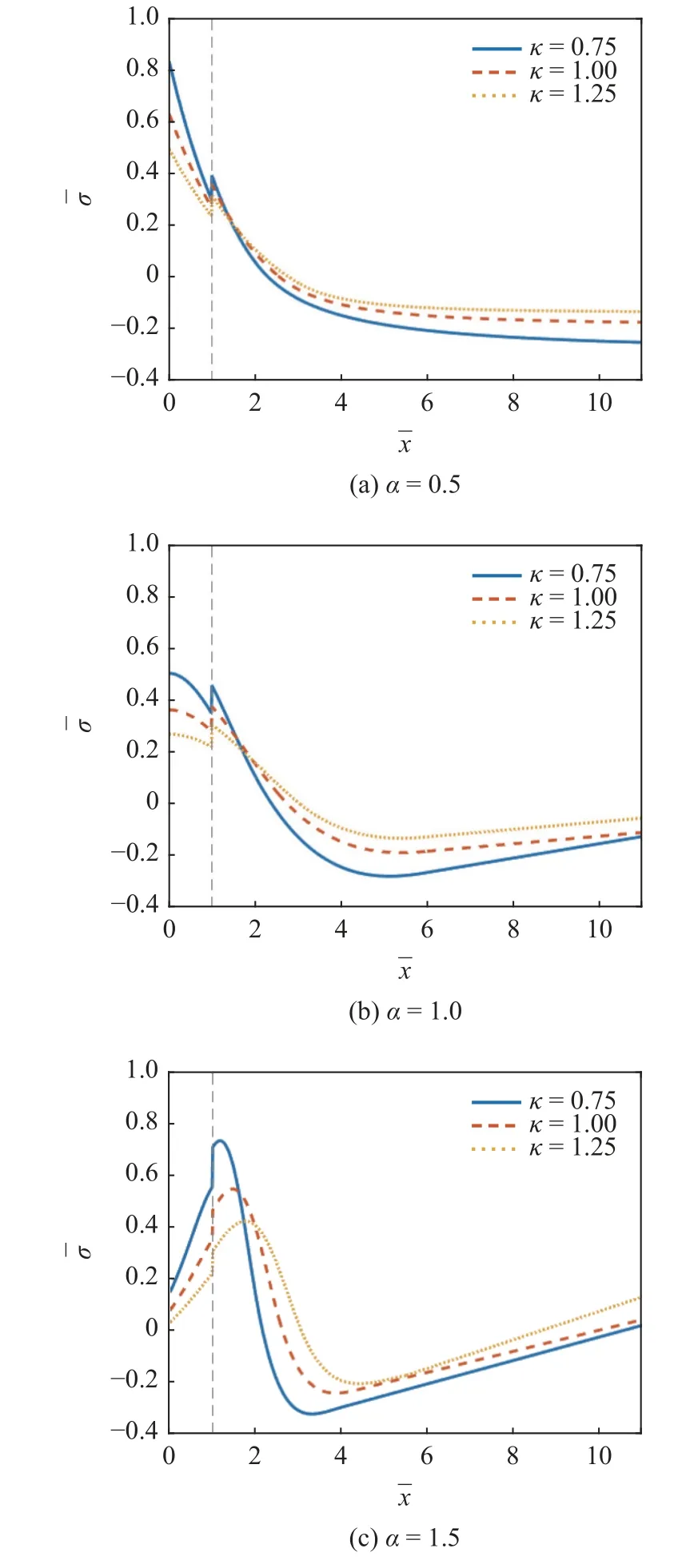
涂层承受的热应力一旦超过其强度极限,其表面将萌生边缘裂纹.必须指出,多数情况下涂层表面分布群体裂纹,为简单起见,本文仅考虑单条边缘裂纹,该裂纹与涂层表面垂直,且裂纹尖端位于涂层之内(a 根据叠加原理及权函数理论[36-37],应力强度因子KI可由权函数与无裂纹体在假想裂纹位置应力乘积的积分得到,即 式中,η 轴的原点位于裂纹口部,如图1(b)所示,η=x+h1,σ (η)=-σ1yy,w(η,a)为权函数,其级数表达式为[38] 式中,Mj为待定系数,通常只需取上式级数中的前3 项就具有足够精度[38].因此,M1,M2和M3可通过两个参考载荷作用下的应力强度因子和一个附加条件确定. 附加条件常取权函数在裂纹口部(η=0)曲率为0[38],即 两种参考载荷可分别取作用在裂纹口部的一对集中力P和作用在裂纹面上的均布载荷σ,因此 式中,KIP和KIσ为两种参考载荷作用下的应力强度因子,FP和Fσ为形状因子. 联立式(37)~式(40),得到M1,M2和M3表达式如下[38] 式(41)中FP和Fσ为待定参数,可以通过有限元方法计算两种参考载荷下的应力强度因子确定.考虑到涂层厚度远小于基体厚度,文献[4]给出了h2/h1=10时FP和Fσ的拟合表达式如下 为简化分析并得到普适性规律,本文引入下列无量纲参数 无量纲温度沿厚度方向的分布规律如图2 所示,图中无量纲时间 κ 依次为0.75,1 和1.25,其他无量纲参数=1.5,=1.5,h2/h1=10.由图可知,温度分布曲线在界面=1 两侧呈现不同斜率,这是由于涂层和基体材料性能差异,两者具有不同的热阻所致.图2(a)和图2(b)分别为分数阶阶次α=0.5(亚扩散)和α=1 (经典扩散)情形,可以看到脉冲热流加载后,无量纲温度沿厚度方向降低.图2(c)表明,当分数阶阶次α=1.5 (超扩散)时,温度沿厚度分布呈现出先增后减的变化趋势,这是因为热流脉冲下的热波在较短时间内突破界面并传递到了基体,涂层温度快速降低,与文献[21]中所描述的分数阶热扩散现象一致. 图2 无量纲温度 在不同时间 κ 下的分布Fig.2 The distribution of the dimensionless temperature for various timesκ 图3 无量纲应力 在不同时间 κ 下的分布Fig.3 The distribution of the dimensionless stress for various timesκ 无量纲热应力强度因子随无量纲时间 κ 的变化规律如图4 所示,其中无量纲参数h2/h1=10,=1,=1.2,=1.5,=1.25,=1.可以看出,热应力强度因子在热流脉冲后的短时间内快速增大,达到峰值后开始下降并逐渐趋于平稳.相对裂纹长度依次取0.25,0.5 和0.75 时,热应力强度因子的峰值逐渐降低,这是由于热应力沿厚度急剧衰减(见图3),从而使较长裂纹裂尖附近的应力水平降低,说明在热流脉冲下较短裂纹更易扩展.当涂层和基体具有相同的材料属性和传热性能时,退化为均质薄板,此时应力强度因子的变化规律与均质板裂纹的变化趋势一致[28].对比图4(a)~图4(c)可知,随着分数阶阶次的增大,热应力强度因子峰值逐渐提高.图4(c)为超扩散(α=1.5)情形下的应力强度因子变化规律,对比图4(b)可以看出,相同长度边缘裂纹的应力强度因子峰值均明显提高,表明采用经典傅里叶导热理论将低估热载荷的破坏程度. 图4 应力强度因子的时间历程Fig.4 The time history of SIF 本文基于Caputo 分数阶导热模型,采用拉普拉斯积分变换和有限余弦积分变换方法得到了涂层-基体系统在热脉冲作用下温度场的封闭解.基于非耦合热弹性理论和权函数法确定涂层边缘裂纹的热应力强度因子.探讨了分数阶阶次对温度场、热应力场和热应力强度因子的影响,以及热应力强度因子随裂纹长度、时间等的变化规律.主要结论如下: (1)分数阶阶次强烈影响涂层-基体系统的热响应速度以及温度场和热应力场; (2)超扩散(1 <α<2)情形下的裂纹尖端热应力强度因子峰值高于经典扩散(α=1)时的峰值,而亚扩散(0 <α<1)情形下裂尖热应力强度因子峰值低于经典扩散时的峰值; (3)热流脉冲作用下,涂层边缘裂纹越长,裂纹尖端应力强度因子峰值越小. 附录A ε0(t)和 ρ (t)的表达式如下[35] 式中5 结果与讨论


6 结论

