面向智能电网能源枢纽的需求响应策略研究

庞思颜，饶 欢，梅傲琪，柳水莲，姚玉斌

（1.广东电网有限责任公司东莞供电局，东莞 523120；2.东方电子股份有限公司，烟台 264000；3.大连海事大学，大连 116026）

0 引言

使系统在负荷高峰期稳定运行是电网公司的重要任务，通常在负荷需求高的时候会增加发电量以维持电力供需平衡[1]。最近，需求侧管理（demand side management,DSM）技术的进步提升了电网需求侧响应水平[2]。需求侧管理可分为几类，如削峰、填谷和负荷的灵活调整[3]。通常情况下需求响应（demand response,需求响应）包括在最后一个类别中。需求响应鼓励客户自愿转移或降低他们的灵活负荷（如洗衣机和空调系统）[4]，可成为电网公司负荷管理的可行解决方案。

在文献[5]中，提出了一种需求响应算法来管理住宅电器的使用时间。在文献[6]中，给出了一种基于实时定价的需求响应方法。在文献[7]中，为需求响应提出了一种称为AAGV的定价机制，可以防止客户的窃电行为。在文献[8]中，将需求响应建模为Stackelberg博弈，以最小化客户的能源消耗成本。需求响应的成功应用取决于客户在管理其能源使用方面的主动性。对电网公司来说，激励客户积极参加需求响应计划仍然是一个挑战[9]。事实上，当客户将他们的用电负荷曲线从无序模式改为计划模式时，对其会产生不适的成本。对现有的需求响应计划进行修改，以降低对客户反应的依赖，可以提高未来智能电网中需求响应的性能[10]。

如热电联产和燃气炉的技术进步，促进了能源网络中多种能源载体的整合[11]。在一个能源枢纽中，如电力和燃气等不同类型的能源，可以被转换、调节和储存[12]。目前有许多关于能源枢纽的投资财务分析，运行策略，以及控制系统的开发[13-15]等内容的研究，但很少有专门针对能源枢纽进行需求响应分析的工作。

在本文中，证明了不同类型能源的整合参与需求响应是一个可行的需求侧管理优化方案，可提高现有需求响应计划的性能。实际上，不同能源载体之间的耦合使客户不仅可以通过负荷转移的方式参与需求响应计划，而且还可以转换其消耗能源来源进行参与。本文把这种针对多能源整合的需求响应计划称为综合需求响应（integrated demand response,IDR）。综合需求响应适用于智能电网中的能源枢纽，基于双向通信网络和信息技术来交换客户和电网公司之间的数据。在能源枢纽中，客户可以通过使用一些转换设备，如微型涡轮机和燃气炉，将一种类型的能源转换为另一种类型的能源，如将燃气转换为电力，从而参与综合需求响应。因此，从电力公司的角度来看，电力负荷需求减少。然而，从客户的角度来看，电力消费并没有改变，但供电的来源却改成了燃气。燃气公司也从综合需求响应中获益，向客户出售更多的燃气来转换为电力。

本文为一组实时定价的能源枢纽提出了一个综合需求响应程序。能源枢纽的客户旨在最大限度地提高他们的日效用，日效用定义为客户从消费能源中获得的满足度效用与支付的总能耗费用之间的差值。在所提出的综合需求响应模型中，能源枢纽和能源公司通过运行分布式算法来确定其最佳策略，从而自动进行互动。经研究发现，综合需求响应问题是一个序数势博弈，证明了该博弈的纳什均衡存在且具有唯一性。综合需求响应计划在一个有6个能源枢纽的智能电网上进行模拟。仿真结果表明，在综合需求响应计划中转换能源可以使客户和能源公司都受益。电网的峰值负荷需求可以大大减少，而客户的用电量不会有很大变化。此外，燃气公司可以出售更多的燃气以获得更高的利润。客户的回报也可以增加30%左右。结果还表明，该算法的运行时间与能源枢纽的数量呈线性增长关系。

1 系统模型

能源枢纽使客户能够将一种类型的能源转化为其他能源。此外，能源枢纽的现代信息技术可为客户提供实时信息，如不同能源的实时价格[16]。特别是，能源管理系统（energy management system,EMS）可以在能源枢纽中使用，通过双向通信系统在能源公司和客户之间交换实时数据。此外，EMS可以向内部转换器设备（如燃气炉和微型涡轮机）发送控制信号，以根据实时数据优化能源枢纽的运行。图1显示了一个连接电力和燃气管网的能源枢纽，为客户提供电能和热能。Eout和Hout分别表示输出的电能和热能功率。Ein和Gin分别表示输入电力和燃气功率。转换设备为变压器、燃气炉和微型涡轮机，效率分别为ηT、ηF、（微型涡轮机的电效率）和（微型涡轮机的热效率）。调度系数用α∈[0,1]表示，它定义了输入到微型涡轮机和燃气炉的燃气比例[17]。在能源枢纽中，EMS控制α以优化燃气到电力的转换。通常，一个能源枢纽可建模为一个线性的二端口系统[18]。输入和输出功率的相互关系如式(1)所示。

图1 能源枢纽示意图

在一个由N个能源枢纽组成的智能电网系统中建立综合需求响应模型。能源枢纽由一家电力公司和一家燃气公司提供服务。N={1,...,N}表示能源枢纽的集合。将每一天划分为T个相等的时间间隔。T={1,...,T}表示时间间隔集合。在以下部分，对综合需求响应计划中的能源供应商和客户双方进行建模。

1.1 能源供应商模型

电力公司的随时间变化的发电成本为ce(Ettotal)。通常情况下，成本函数ce可认为是凸函数，具有正导数。对电力公司使用的是一个有两步的分段线性成本函数。图2(a)给出了本文所使用的两阶段成本函数。成本函数斜率sl1和sl2由电网公司预先给出，电力公司的目标是使其利润最大化。给定电价pe(t)，电网公司向客户提供一定数量的电能，解决以下优化问题：

图2 能源价格函数

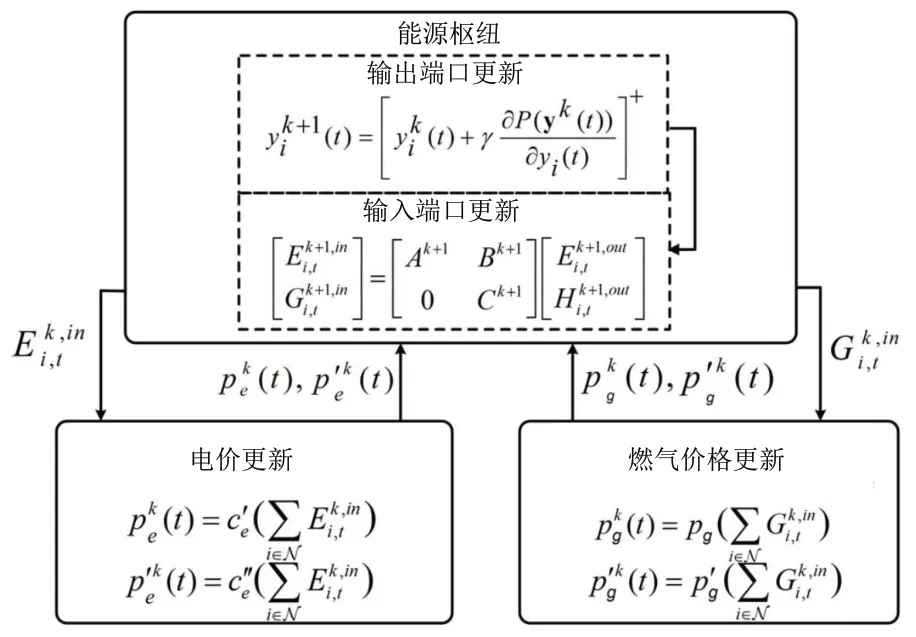
图3 能源公司和能源枢纽之间的交互

上述优化问题的解为：

式中c′e(g)是函数ce(g)的导数。式(5)意味着电价等于边际发电成本。

在燃气网络中，价格主要由供应和需求的基本因素驱动。燃气价格也可能取决于原油价格[19]。pg(Gttotal)表示供应燃气的价格函数。在本文中，假设采用阶梯式费率结构来模拟燃气价格。图2(b)显示了不同水平Gttotal的燃气价格等级。这个模型在实践中被广泛使用。

1.2 客户模型

3）能源枢纽的不同客户对电力和燃气价格方案的不同反应可以通过微观经济学中的效用函数来模拟[20]。效用函数以货币单位衡量，它模拟了能源枢纽的客户在不同时间段的满足度。表示能源枢纽i的客户在时间t达到的效用。对电力和燃气使用的二次效用函数如下：

4）假设能源枢纽的客户有价格预期。其使用EMS来接收关于电力和燃气价格的信息。

博弈论提供了一个框架来分析参与能源枢纽之间的价格互动。在综合需求响应博弈中，能源枢纽i的策略是：

x-i表示除能源枢纽i之外的所有能源枢纽的策略情况，它定义为x-i=(x1,...,xi-1,xi+1,...,xN)。能源枢纽i的客户效用为：

约束条件为式(6)～式(9)。

将式(1)中给出的矩阵倒置，可得：

式中：

从式(11)中，可得：

将式(15)和式(16)代入式(11)，xi将被转换为一个等价的策略yi，如下所示：

将式(15)和式(16)代入式(12)，策略yi是以下优化问题的解：

约束条件为式(6)～式(9)和式(20)。

定义1：如果一个博弈有一个序数势函数P(y)，则称其为序数势博弈[21]。对于y=(yi,y-i)和，有：

式(22)中的综合需求响应博弈是一个序数势博弈,其势函数如下：

在式(24)中，m是一个正整数。参数m没有任何物理意义，只是用来定义势函数。文献[21]证明参数m需要足够大，以便式(24)中的势函数满足式(23)中的必要条件。因此，纳什均衡中能源枢纽的策略y*是以下问题的解：

约束条件为式(6)～式(9)和式(20)。在势博弈式(25)中，所有参与者的报酬函数都映射到势函数P(y)上。当m是一个足够大的整数时，式(17)中势函数P(y)是严格的凹函数。

定理1：设G是一个具有势函数P的势博弈，设Gμ是与G结构相同的博弈，但所有玩家的报酬函数都用势函数P取代。G的纳什均衡集与Gμ的纳什均衡集重合。此外，对于可行集：如果P是凹函数，x*是G的纳什均衡，x∈Pmax，如果P是严格凹的，则均衡是唯一的，其中Pmax是P的最大值集和；如果P是凸函数，x*是G的纳什均衡，那么x∈Pmin，如果P是严格凸的，则均衡是唯一的，其中Pmin是P的最小值集和，证明可参见文献[22]。

定理2指出，势函数式(24)的最优点对应于综合需求响应博弈的纳什均衡。严格凹的势函数(17)有唯一的最优点。因此，博弈式(22)有唯一的纳什均衡。在下一节中，将研究迭代算法来确定所提出的综合需求响应博弈的纳什均衡。

2 综合需求响应算法

3 仿真评估

使用一个示范性的案例来评估所提出的综合需求响应算法的性能。考虑六个能源枢纽，每个枢纽平均有150个客户，由一家电力公司和一家燃气公司服务。每个能源枢纽的变压器、燃气炉和微型涡轮机的效率参数ηT、ηF、和分别从[0.9,0.98]、[0.93,0.97]、[0.35,0.45]和[0.4,0.5]的区间随机选择。将一天划分为T=24个时段。发电成本函数ce(·)曲线的斜率为sl2=455元/MWh，sl1=245元/MWh[18]。对于燃气价格函数，假设系统中对应不同的负荷水平有三个价格档次：Gttatal＜4的低价；4＜Gttatal＜5的中等价；5＜Gttatal的高价。低、中、高价格水平为1、2和3元/m3。考虑用两天时间（共48小时）进行模拟。在第一天，燃气价格为3元/m3。在第二天，燃气价格为1元/m3。为了模拟客户的效用函数，第一天中参数vi,t从区间[3,6]中随机选择。对于第二天的16-22时间段，vi,t从[6,12]中随机选择，从[3,6]中随机选择第二天其他时段的vi,t。这意味着客户在第二天的第16～22个时段消费电力或燃气的效用更高。对于所有的能源枢纽，参数βi,t设定为0.5。在不使用综合需求响应的情况下，调度因子αi,t设定为0.6。此外，约束条件式(8)和式(9)中的最低和最高限额分别比不使用综合需求响应的负荷需求低或高30%。也就是说，能源枢纽的客户在每个时间段最多可以增加或减少30%的电力和供热需求。

1）对于基本负荷，不可控制；

2）可转移负荷，可由每个能源枢纽的EMS控制。在图中，基本负荷曲线由绿色虚线表示。图4显示了使用和不使用综合需求响应时的总电力输入功率。电力输入功率是由电力公司直接产生的。电力公司使用综合需求响应来减少电力输入的峰值以降低其发电成本。在没有综合需求响应的情况下，每天的17～21个时段都会出现峰值。

图4 使用或不使用IDR时输入电功率

在第一天，燃气价格很高。因此，枢纽的客户更愿意转移他们的负荷需求，而不是购买燃气来转换为电力。图4显示，发电量曲线变得更平坦，峰值负荷减少了27%。图5显示了客户方所消耗的总电力输出功率。该图证实了客户修改了他们的用电模式，直到在t=18达到约束条件(8)规定的下限，因为将燃气转换为电力是无利可图的。图6显示了从燃气公司购买的燃气总量。可以观察到，由于第一天的燃气价格较高，使用综合需求响应计划减少了燃气购买量。图7显示了用户方面的燃气消费总量（即供热需求）。可以看出，供热需求变得更加平缓，几乎与从燃气公司购买的燃气相等。总之，当燃气价格较高时，将燃气转换为电力是无利可图的。因此，用户只愿意通过将其负荷需求从高峰期转移到非高峰期来参与综合需求响应。此外，如图8所示，调度系数α非常低（每个能源枢纽约为0.2），这证实了当燃气价格高时，不会将燃气转换为电力。

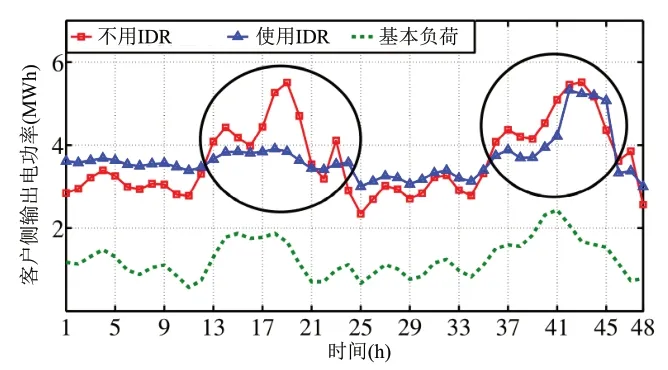
图5 使用或不使用IDR时输出电功率

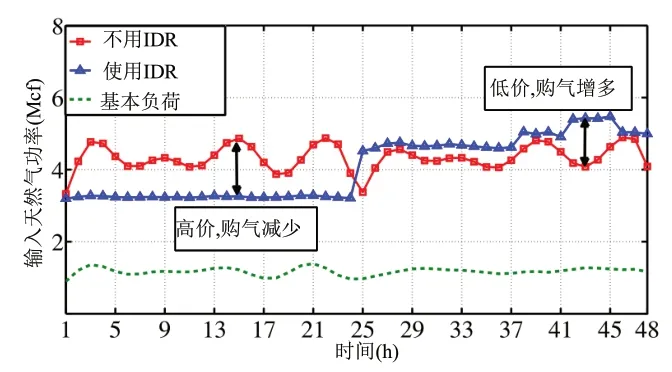
图6 使用或不使用IDR时输入燃气功率

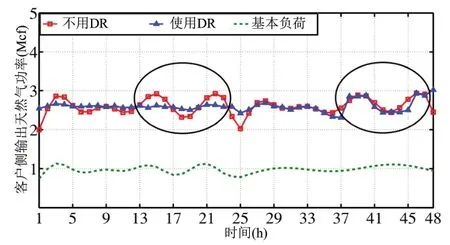
图7 使用或不使用IDR时输出燃气功率

在第二天，燃气价格很低。因此，将燃气转化为电力可得到收益。图4显示，发电曲线变得更平坦，峰值负荷减少了47%。图5证实了客户不需要像第一天那样修改他们的用电模式，因为现在将燃气转换为电力是有利可图。因此，他们购买燃气并将其转换为电力用于日常消费。因此，他们不向电力公司购买电力。图6显示，由于综合需求响应的价格较低，从燃气公司购买的燃气有所增加。此外，用户在41～45时段需要更多的电力，因此他们在这个时间段购买更多的燃气来转换为电力，如图6所示，观察到在41～45时段出现购买燃气的高峰。图7显示，有综合需求响应和没有综合需求响应的供热需求几乎相同。因此，在综合需求响应项目中，用户也不需要修改他们的供热消费。总之，当燃气价格较低时，将燃气转换为电力是有利可图。因此，客户更愿意通过将燃气转换为电力来参与综合需求响应，而不是修改他们的电力和供热消费情况。综合需求响应的这一特点减少了对客户反应的依赖性。此外，如图8所示，参数α约为0.8，在高峰时段41～45则变为1。这证实了在综合需求响应计划中，当燃气价格较低时，更多燃气转化为电力。

图9给出了所有能源枢纽在这两天的日回报情况。通过参与综合需求响应计划，客户方的日回报增加约30%。图10给出了参加和不参加综合需求响应的电力和燃气公司的日利润。电力公司的日收益随着综合需求响应算法的实施而增加，因为负荷曲线变得更平坦，所以发电成本明显下降。燃气公司的利润也随着综合需求响应而增加。事实上，能源枢纽在第二天购买了更多的燃气，以便在高峰时段将其转化为电力。因此，燃气公司通过出售更多的燃气获得了更高的利润。

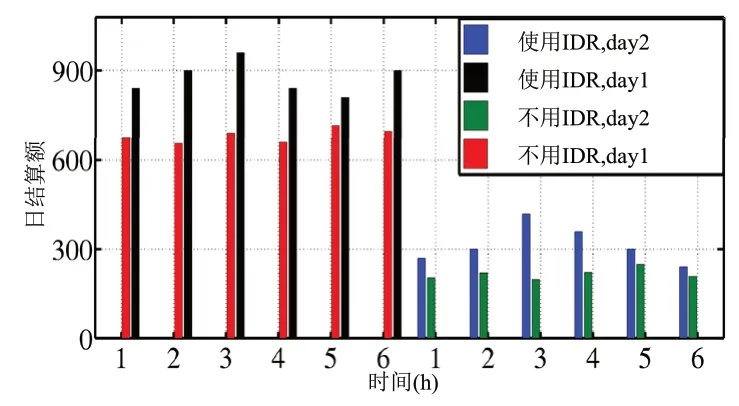
图9 使用或不使用IDR时能源枢纽日收益

图10 使用或不使用IDR时能源公司收益

使用了一台处理器为Intel Core i5 10400 @2.9GHz平台进行仿真。图11显示了能源枢纽1的电力和燃气输入和输出功率在时段10的收敛情况。步长γ为0.09。在大约80次迭代后收敛。对不同数量的能源枢纽运行该算法。图12显示，运行时间随着能源枢纽数量的增加而线性增加，对于一千个枢纽的大型系统，计算时间仅为40s，这证实了所提出的算法可以用于有大量能源枢纽的场景。

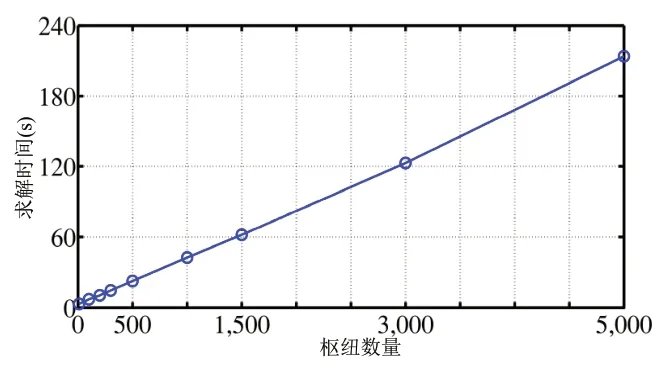
图12 不同能源枢纽数量情况下的计算时间

4 结语

本文提出了一种新的能源枢纽的综合需求响应方案，以减少对现有需求响应方案中客户反应的依赖。将所提出的综合需求响应计划建模为一个具有唯一纳什均衡的序数势博弈。仿真结果表明，客户既可以通过转移他们的负荷需求，也可以通过转换他们的能源来源来参与综合需求响应计划。结果显示，当燃气价格较高时，客户更愿意像传统的需求响应计划那样转移他们的负荷。然而，当燃气价格较低时，他们有一个新的选择，即在微型涡轮机中将燃气转换成电力，以减少能源峰值需求。因此，综合需求响应可以减少对客户积极性和动力的依赖。与传统的需求响应方法相比，在能源枢纽的综合需求响应中，客户反应依赖度低，且计算时间满足系统中存在大量能源枢纽的场景。