探究使用粒子群算法优化电机PI控制效果及耗费时间
李文正,张稳桥,曾晓松
(贵州航天林泉电机有限公司,贵州 贵阳 550081)
0 引言
实际船舶推进电机运行中主要采用经典的PI控制来维护船舶正常航行。通常情况下,PI控制器的参数主要在设备出厂时根据工程设计的方法,按照图纸要求并结合系统要求进行设定,在船舶航行中根据航行需要由经验丰富的轮机长通过微调控制推进电机。但是在对船舶推进电机模型进行仿真时,由于缺乏调节器的精确结构和调节的丰富经验,模型的控制参数往往无法精确得到,只能根据数学模型和仿真数据不断调整控制参数,调整过程不仅繁琐、耗时,且整定结果有时并不理想。
粒子群算法(particle swarm optimization,PSO)作为一种群体迭代算法,是由Kenndy和Eberhart[1-2]在1995年提出的群智能搜索的策略,通过模拟鸟类在自然界中捕食时行为,将其抽象为数学理论而提出的一种智能优化算法,其优点相比其他算法而言需要整定的参数更少,不存在交叉和变异过程,通过并行计算,收敛速度更快。
文中根据粒子群算法强大的寻优能力,利用搭建好的仿真模型,针对推进电机仿真模型的速度调节器(ASR)、转矩调节器(ATR)和磁链调节器(AψR)等控制参数在静态负荷和动态负荷模型两种情况下进行整定,探究不同情况下粒子群算法的寻优速度和整定效果。
1 粒子群算法基本原理
PSO算法首先会初始化一群粒子,确定参数维度N、参数范围(即每个粒子的初始位置),每个粒子代表该优化问题的一个最优解决方案,通过个体极值和群体极值更新自身的速度和位置,对目标函数进行整定或优化,详细过程如图1所示[3]。
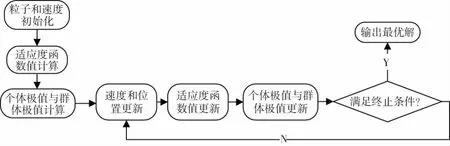
图1 PSO算法寻优过程
设N维空间中有m个粒子,Xi=(xi1,xi2,K,xiN)是粒子i(i=1,2,K,m)的当前位置,Vi=(vi1,vi2,K,viN)是粒子i的当前速度,Pi=(Pi1,Pi2,K,PiN)是粒子i的最优位置,对应适应值为个体的最优解pbesti。令f(x)为目标函数,则微粒i当前的最优位置为[4-5]:
(1)
式中,t为粒子的进化代数。
群体中所有粒子的全局最优位置为:
Pg(t)∈{P1(t),P2(t),…,Pm(t)|f(Pg(t))}
=min{f(P1(t)),f(P2(t)),…,f(Pm(t))}
(2)
每次迭代后粒子的速度与位置更新的公式为:
(3)
式中,i=1,2,…,m;j=1,2,…,n;c1、c2为学习因子,分别是微粒飞向自身最好位置的步长和飞向全局最好位置的步长,r1、r2是分布于[0,1]区间的随机数;ω为惯性因子。
为了获得更好的动态惯性因子ω和更好的寻优效果,文中采用的是Shi等[6]建议的线性递减权值策略,如式(4):
(4)
式中,ωmax和ωmin分别为初始的惯性权重值和迭代至最大次数的惯性权重;F是函数的迭代次数;T为惯性权重保持线性递减的最大迭代次数;超过T后ω保持不变。
2 粒子群优化推进电机模型
2.1 推进电机仿真模型
文中根据中能LNG“CESI GLADSTONE”船舶三相异步推进电机为例,在dq同步旋转坐标系的电压、磁链和转矩方程为[7]:
(5)
(6)
(7)
通过dq同步旋转坐标下电压、磁链和转矩方程在Matlab/Simulink仿真软件下搭建电流滞环控制推进电机仿真模型,如图2所示。

图2 推进电机电流滞环控制
在实际情况下推进电机带动螺旋桨推动电力推进船舶在海上正常航行,因此在搭建动态负荷下推进电机仿真模型时还需要对船机桨模型进行搭建。
2.2 螺旋桨仿真模型
根据螺旋桨的工作原理可知,当螺旋桨转速n≠0时且螺旋桨的进速VP≠0时,在定常状态下(即船舶在航行过程中装载、气候、海面状况等条件不变)螺旋桨的推力P、修正进速比J’和转矩T可表示为:
(8)
式中,D为螺旋桨直径;KP′为螺旋桨推力修正系数;KT′为转矩修正系数;Vs为船速;τ为伴流系数。
考虑螺旋桨在水中产生推力带动船舶航行,假设船舶沿某一航向直线运行,则船舶直线运动方程为:
(9)
式中:R为水对船舶运动产生的总阻力;r为阻力系数,与船体线型、载重、污底、拖带、航道及海洋环境等因素有关。
根据螺旋桨仿真模型分析得到螺旋桨模型结构图,如图3所示。
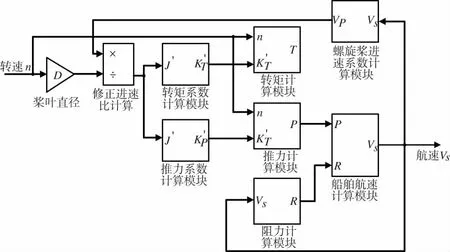
图3 船桨模型结构图
2.3 粒子群优化推进电机仿真模型
(1)粒子群算法优化推进电机动态仿真模型
根据误差积分准则[8]ITAE(Integral performance index)即系统期望输出与实际输出的偏差和时间乘积的积分通过粒子群算法对推进电机动态仿真模型的控制参数进行整定优化。粒子群优化的动态推进电机仿真模型如图4所示。
在进行粒子群算法优化整定推进电机电流动态模型控制参数的过程中,将各个调节器中KP、KI参数,在设定的比例系数和积分系数的范围内通过输出转矩、磁链、电流、转速等各个调节器的反馈结果通过误差性能评价指标判断,当不满足粒子群的评价指标时通过对各个调节器的参数进行不断修正,寻找模型中各调节器的控制参数的最佳值,获得最佳的优化效果[9-10]。具体的粒子群优化推进电机PI控制的仿真流程和算法的部分代码分别如图5和图6所示。

图5 PSO优化PI过程示意图

图6 粒子群算法部分仿真代码
粒子群算法优化的推进电机动态仿真结果如图7、图8所示。

图7 动态负荷下转速响应曲线随迭代次数的变化

图8 动态负荷下调节时间随迭代次数的变化
(2)粒子群算法优化推进电机静态仿真模型
为了降低粒子群算法优化推进电机动态仿真模型的难度,文章根据螺旋桨负载的实际效果,结合数学模型将船体动态模型简化为固定的静态负载,对推进电机静态模型控制参数采用粒子群优化,其仿真模型和仿真结果分别如图9-图11所示。
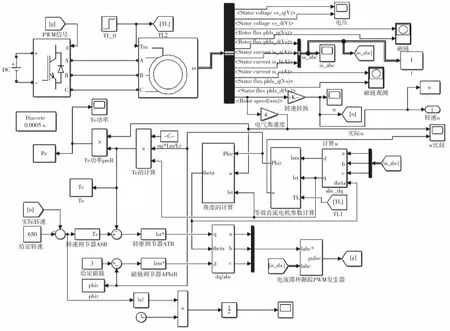
图9 静态负荷下推进电机电流滞环控制
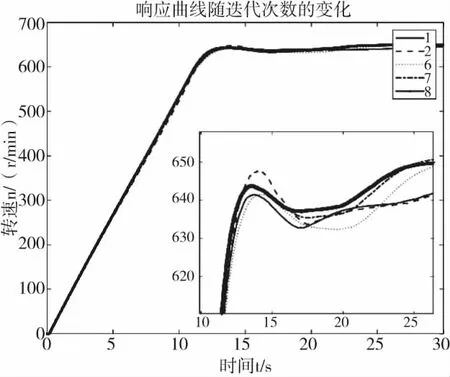
图10 静态负荷下转速响应曲线随迭代次数的变化

图11 静态负荷下调节时间随迭代次数的变化
(3)静态负荷下优化的PI参数对动态负荷下推进电机控制
为了验证粒子群算法优化静态负荷下推进电机的控制参数在动态负荷下推进电机仿真模型的控制效果,文中将第二部分迭代20次后静态负荷下推进电机PI控制参数代入动态负荷下推进电机仿真模型,如图4所示,并与迭代20次动态负荷下PI控制参数仿真效果进行对比,其仿真结果如图12所示。

图12 不同迭代方式下电机转速情况
根据粒子群算法优化两种情况下推进电机电流滞环控制仿真结果可以看出,对比图7和图10两种情况下转速响应曲线随迭代次数的变化可以看出,采用粒子群算法优化动态负荷下推进电机转速曲线和静态负荷下推进电机转速曲线均可以在650 r/min左右保持稳定,并通过图12中不同迭代情况下电机转速曲线对比分析可知,采用静态负荷对推进电机进行仿真在不考虑环境扰动对模型产生的影响上可以代替动态负荷下推进电机仿真模型。
此外,对图8和图11两种情况下调节时间随迭代次数的变化进行整理,如表1所示,可以看出当采用粒子群算法优化推进电机动态仿真模型总耗时为297.06 min,而采用粒子群算法优化推进电机静态仿真模型总耗时为148.4 min,通过简单的数学分析,可以得出采用粒子群算法优化推进电机静态负荷相比优化推进电机动态负荷仿真模型在相同的迭代次数下整个模型的仿真运行时间提升了50%。

表1 两种粒子群迭代时间对标
3 结论
文中针对静态负荷和动态负荷两种不同情况下推进电机仿真模型采用粒子群算法优化PI控制参数,通过两者之间转速仿真曲线、调节时间随迭代次数变化以及两者仿真运行时间总耗时的分析对比,可以得出,在仿真模型搭建过程中为了简化模型搭建难度、提高粒子群算法优化速率,可以针对实际情况对部分仿真模型进行适当简化,如可将船桨等动态模型简化为静态负荷,降低仿真模型搭建难度,提高仿真运行速率。

