不同强度钢筋考虑屈曲的低周疲劳损伤模型

杨红 彭荣盛 赵银

DOI： 10.11835/j.issn.2096-6717.2022.092

收稿日期：2022?05?28

基金项目：国家自然科学基金（51878100）

作者简介：杨红（1969- ），男，博士，教授，博士生导师，主要从事钢筋混凝土基本性能及结构抗震研究，E-mail：yangh@cqu.edu.cn。

Received： 2022?05?28

Foundation item： National Natural Science Foundation of China （No. 51878100）

Author brief： YANG Hong （1969- ）， PhD， professor， doctorial supervisor， main research interests： behavior and seismic design of reinforced concrete structures， E-mail： yangh@cqu.edu.cn.

摘要：钢筋混凝土柱受力后期的重要非弹性特征之一是纵向钢筋受压屈曲，以及反复拉压之后断裂，但可考虑钢筋屈曲的低周疲劳损伤模型很少，且少数考虑屈曲的疲劳损伤模型无法直接用于不同强度钢筋的疲劳损伤计算和断裂分析。对长径比为6.25、9.375、12.0、15.0的HRB400钢筋、HRB500钢筋试件分别进行考虑屈曲的拉压相等循环加载、拉压不等循环加载试验，测量平均应力-平均应变（σ ?_s-ε ?_s）曲线和跨中横向屈曲位移。与HRB600钢筋的相应试验结果结合，形成系统性试验数据。基于试验数据分析屈服强度、长径比对屈曲钢筋极限变形能力的影响，考察传统C-M疲劳寿命模型、基于总平均应变幅ε ?_sa的修正C-M模型对屈曲钢筋的适用性，并分析误差原因；提出适用性较好的基于循环总平均应变幅ε ?sa-cyc的修正C-M疲劳模型。结果表明：由于钢筋的ε_su、ε_sult和f_u等力学性能参数不同，不同强度钢筋试件屈曲后的低周疲劳受力性能存在差异；屈曲钢筋循环受力时的极限变形能力与低周疲劳损伤有关，仅根据单调受拉的极限拉应变ε_su不能正确判断钢筋的断裂状态；基于总平均应变幅ε ?_sa的修正C-M模型无法合理考虑不同加载方式对屈曲钢筋低周疲劳寿命的影响，存在系统误差；基于ε ?sa-cyc的修正C-M模型可合理考虑不同加载方式的影响，能直接用于不同强度、不同长径比钢筋，且误差较小。

关键词：钢筋混凝土柱；屈曲；低周疲劳；疲劳寿命模型；加载方式

中图分类号：TU375.3     文献标志码：A     文章编号：2096-6717（2023）05-0147-14

Low-cycle fatigue damage model of buckled steel bar with different strength

YANG Honga，b， PENG Rongshenga， ZHAO Yinb

（a. School of Civil Engineering； b. Key Laboratory of New Technology for Construction of Cities in Mountain Area， Ministry of Education， Chongqing University， Chongqing 400045， P. R. China）

Abstract： One of the important inelastic characteristics of reinforced concrete columns during the strain-softening stage is the buckling and the fracture of longitudinal reinforcement after tension-compression cyclic loading. However， there are few low cycle fatigue damage models considering the influence of buckling， and a few fatigue damage models considering buckling cannot be directly used for fatigue damage calculation and fracture analysis of steel bar with different strength. In this paper， the specimens of HRB400 reinforcement and HRB500 reinforcement with slenderness ratios of 6.25， 9.375， 12.0 and 15.0 were subjected to tension compression equal cyclic loading and tension compression unequal cyclic loading considering buckling respectively. The average stress-strain （σ ?_s-ε ?_s） curves and mid-span transverse displacements of buckled specimens were measured. Combined with the corresponding test results of HRB600 reinforcement completed by the author， a systematic test data was constituted. Based on the test results， the effects of yield strength and slenderness ratio on the ultimate deformation capacity of buckled reinforcement were analyzed， the applicability of the traditional low cycle fatigue damage model （C-M model） and the modified C-M model based on the total average strain amplitude ε ?_sa to the buckled reinforcement was investigated， and the errors were analyzed. A modified C-M fatigue damage model based on cyclic total average strain amplitude ε ?sa-cyc with good applicability was proposed. The results show that specimens with different strength have different low cycle fatigue performance due to the different mechanical properties of steel bar， such as ε_su，ε_sult and f_u etc. The ultimate deformation capacity of buckled steel bar under cyclic loading is related to low cycle fatigue damage， the fracture of steel bars cannot be correctly determined by the ultimate tensile strain ε_su under monotonic tension. The modified C-M model based on the total average strain amplitude ε ?_sa cannot reasonably consider the influence of different loading methods on the low cycle fatigue life of buckled reinforcement， and there are systematic errors. The modified C-M model based on ε ?sa-cyc can reasonably consider the influence of different loading methods， and can be directly used for reinforcement of different strength and slenderness ratio with small error.

Keywords： reinforced concrete columns； buckling； low cycle fatigue； fatigue life model； loading method

强烈地震作用下钢筋混凝土（RC）框架结构若干预设部位（如梁、柱端部塑性铰区）将出现明显的非弹性变形和损伤[1]。在强震引起的循环受力过程中，柱端塑性铰区除发生混凝土开裂、压碎、剥落外，柱纵向钢筋会经历高应变（大于屈服应变）、低周反复拉压受力[2]。在此过程中，一方面，纵筋应变超过约4～10倍屈服应变后容易发生屈曲[3-4]，即柱纵筋受压向外鼓出、侧向弯曲；另一方面，屈曲后的柱纵筋容易在随后的反复拉压受力过程中断裂，导致RC柱失去承载力。

大量震害调查和试验研究表明，纵筋屈曲、断裂是RC柱受力后期的重要非弹性特征[5-8]，其中，柱纵筋断裂由钢筋的低周疲劳性能控制[9]。因此，研究钢筋在屈曲状态下的反复拉、压受力性能，并采用合适的疲劳寿命模型正确描述屈曲钢筋在循环受力过程中的低周疲劳损伤，对合理评价RC柱的抗震性能和柱纵筋的断裂状况非常关键。

目前，关于钢筋低周疲劳受力性能的已有研究成果较少考虑屈曲的影响。Coffin[10]和Manson[11]建立的经典C-M疲劳模型给出了塑性应变幅与失效前循环周数的关系；Wang等[12]和Koh等[13]建议了基于钢筋总应变幅的疲劳损伤模型；McCabe等[14]和Mander等[15]则从能量的概念出发，提出了低周疲劳损伤模型；Hawileh等[16]根据BS 460B和BS B500B钢筋的低周疲劳试验结果，分别对基于塑性应变幅、总应变幅的疲劳损伤模型进行了验证。此外，一些学者对中国生产钢筋的低周疲劳性能进行了研究，如张耀庭等[17]、郑家良等[18]和孙传智等[19]分别对HRB400钢筋、HRB500钢筋和630 MPa级钢筋的高应变低周疲劳性能进行了试验研究，并根据试验数据回归了分别适用于上述3种钢筋的C-M模型疲劳参数取值。值得注意的是，上述低周疲劳损伤模型均基于单轴循环拉压钢筋的试验结果进行研究，未考虑屈曲的影响。

若将上述未考虑屈曲的疲劳损伤模型直接用于相应强度钢筋的低周疲劳损伤计算，其结果一般将明显高估屈曲钢筋的疲劳寿命、错误预测屈曲钢筋的断裂时刻。原因在于，钢筋屈曲之前处于单轴受力状态，其低周疲劳特性主要与钢筋自身的材料性能有关；钢筋屈曲之后处于压弯或拉弯受力状态，需同时考虑几何非线性、材料非线性的影响[20]。两种非线性的耦合效应会使屈曲钢筋的材料非线性程度加重，并在屈曲钢筋的中部弯曲部位形成局部塑性变形集中[21]，且塑性应变集中会促进微裂缝发展、加重损伤程度[22]。因此，屈曲一方面会引起钢筋的受压强度、刚度退化[23-24]，另一方面还会加重钢筋的疲劳损伤和断裂[2， 21]。

少数学者对考虑钢筋屈曲效应影响的低周疲劳损伤模型进行了研究。Kunnath等[21]对按美国ASTM A-615和ASTM A-706标准生产的#11钢筋（直径D_s=35.8 mm，屈服强度f_y=487.48 MPa）进行了高应变低周疲劳性能试验，并强调应重视屈曲对钢筋疲劳寿命的影响，但其仅对固定长径比（L_s?D_s ，L_s为钢筋试件的屈曲长度）的钢筋试件进行了考虑屈曲的循环加载试验，然后根据试验结果回归了C-M模型的疲劳参数取值，显然，该C-M模型仅适用于L_s?D_s 与试验试件取值相同的钢筋。Kashani等[25]、Tripathi等[26]和杨红等[27-28]则建立了在数学表达式中可直接考虑不同L_s?D_s 对屈曲影响的修正C-M模型，其中，Kashani等[25]基于试验结果研究了屈曲对英国生产的BS 500B带肋钢筋（f_y=535.67～544.33 MPa）低周疲劳损伤的影响，并建议了基于总平均应变幅（ε ?_sa）的修正C-M模型；Tripathi等[26]研究了新西兰生产的300E和500E变形钢筋（f_y分别为311.45、511.30 MPa）考虑屈曲的低周疲劳性能，分别提出了基于总平均应变幅ε ?_sa或基于总耗散能量?W_Total的修正C-M模型；杨红等[27-28]对中国生产的HRB400钢筋、HRB600钢筋进行了循环加载试验，研究了屈曲对钢筋低周疲劳损伤的影响，分别基于塑性平均应变幅ε ?_sp和塑性局部应变幅平均值ε ?_（sp，b，avg）建议了适用于HRB400钢筋的修正C-M模型[27]，以及基于循環总平均应变幅ε ?sa-cyc建议了适用于HRB600钢筋的修正C-M模型[28]。

上述几种考虑屈曲的修正C-M疲劳模型的主要缺点是：由于各研究者完成的考虑屈曲的低周疲劳性能试验重点考察长径比的影响，仅针对某特定屈服强度的钢筋试件进行分析，从而使得基于试验结果建立的上述各修正C-M疲劳模型难以直接用于不同强度钢筋。事实上，随着强度的提高，钢筋的变形能力逐渐下降、极限拉应变（与单调受拉断裂相对应）逐渐减小是客观规律，故从理论上看，屈曲钢筋的低周疲劳性能将随强度的提高而逐渐劣化。但是，由于目前缺乏不同强度钢筋低周疲劳性能的系统性试验结果，故检验上述几种修正C-M模型的有效性时，各研究者均只能基于某特定强度钢筋的低周疲劳性能试验结果进行校核，从而使得这些修正C-M模型并不能合理考虑不同强度钢筋屈曲后低周疲劳性能的差异。

此外，不同国家生产的钢筋，其制作工艺、化学成分、微量元素（钒、钛、铌等）等存在差异，故Kunnath等[21]、Kashani等[25]和Tripathi等[26]基于500 MPa级钢筋的试验成果得到的修正C-M模型对中国生产的HRB500钢筋并不直接适用。杨红等[27]提出的适用于HRB400钢筋的修正C-M模型误差仍偏大，这是由于其试验是通过固定屈曲长度（L_s=100 mm或150 mm）、变化D_s形成不同长径比的钢筋试件，这种方法使各试件的材料性能存在一定差异，例如，其钢筋试件的直径D_s分别为12、14、16、18、20 mm，对应的屈服强度f_y分别为460.72、449.33、457.86、456.64、477.78 MPa。

针对以上问题，笔者对16根HRB400和HRB500钢筋试件进行考虑屈曲的循环拉压试验，将该结果与笔者完成的HRB600钢筋的相应试验结果[28]相结合，形成系统性试验数据，并据此分析屈服强度、长径比对钢筋试件高应变低周疲劳性能的影响。基于该试验结果分析已有修正C-M模型的适用性和误差原因，并提出能合理考虑屈服强度和长径比对屈曲钢筋低周疲劳寿命影响的修正C-M模型。

1 单调受拉试验

为避免材料性能不同对考虑屈曲的循环拉压试验结果的干扰，采用与文献[28]相同的做法，各钢筋试件均来源于同一根9 m的HRB400钢筋母材或HRB500钢筋母材，这2根钢筋母材均为在中国商业化生产、符合GB/T 1499.2—2018[29]要求的产品。进行的单调受拉试验、循环拉压试验均在INSTRON电液伺服单轴材料试验机上完成。

在进行考虑屈曲的循环拉压试验之前，对钢筋母材进行了材性试验，所得结果见表1，其中试件编号的含义是，以“Y4-1”为例，“Y4”表示HRB400钢筋（ “Y5”表示HRB500钢筋），“1”表示在母材上随机截取的3个钢筋试件的序号。

由表1可知，3个试件的材性试验结果非常相近。在后文分析中，HRB400钢筋和HRB500钢筋的f_y、E_s等力学特性参数以及单调受拉的应力-应变（σ_s-ε_s）关系均分别取3个钢筋试件试验结果的平均值。

2 考虑屈曲的循环拉压试验

2.1 试验方法

为使不同屈服强度钢筋的试验结果具有系统性，采用与文献[28]相同的试验装置、加载制度、测量方法对HRB400钢筋和HRB500钢筋进行考虑屈曲的循环加载试验。这两类钢筋各设计了8个钢筋试件，分别对应4种长径比（L_s?D_s =6.25、9.375、12.0、15.0）、2种加载方式（拉压相等循环加载、拉压不等循环加载）。

参考Kunnath等[21]的建议，各钢筋试件均采用位移控制加载。为反映在RC构件低周反复加载试验的常用加载制度下RC柱纵向钢筋的应变规律和受力特点，采用如下2种位移控制的加载方法。

1）拉压相等循环加载：按0→3?L_sy→0→-3?L_sy→0→6?L_sy→0→-6?L_sy→……的方法确定每一级加载位移?L_s的取值，其中屈服位移?L_sy=L_s ε_sy，式中ε_sy为受拉屈服应变，ε_sy=f_y?E_s ，f_y和E_s按表1确定。

2）拉压不等循环加载：按0→4.5?L_sy→0→-1.5?L_sy→0→9?L_sy→0→-3?L_sy→……的方法确定各级加载位移?L_s的取值。

各试件按上述加载制度在每一级加载位移幅值下均循环2周，直至钢筋断裂。在循环加载试验正式开始前，对各试件按0.35f_y施加轴向拉力进行预加载，以便调直试件、消除初始偏心。

试验过程中，通过传感器采集INSTRON试验机对钢筋试件施加的轴向力（P），采用百分表测量屈曲钢筋沿轴向的长度变化量（?L_s），试验装置参见文献[28]中图2（a）。根据P和?L_s的测量数据，可得到各钢筋试件的平均应力-平均应变（σ ?_s-ε ?_s）曲线，其中σ ?_s=P?A_s ，ε ?_s=（?L_s）?L_s ，式中A_s为钢筋的名义截面面积，L_s的定义如前文所述。应说明的是，钢筋屈曲后，试件跨中关键弯曲部位的截面应变分布明显不均匀[27]，与单轴材料始终全截面均匀受拉、均匀受压的受力特征明显不同。采用平均应力σ ?_s和平均应变ε ?_s描述钢筋的屈曲受力性能可大幅简化分析过程，这是学术界长期采用的统一做法[2-4， 20-24]，其实质是将屈曲钢筋视为未弯曲且轴向拉压变形相同的钢筋试件进行计算，但需考虑屈曲效应对钢筋σ ?_s-ε ?_s曲线、低周疲劳性能的不利影响。

试验过程中，通过与各试件中点处引出的两根正交布置的细铜丝连接的百分表测量了钢筋的屈曲横向位移（如文献[28]中图2（b）所示），据此可绘制各钢筋试件的强轴方向（钢筋纵肋方向）、弱轴方向（钢筋纵肋的垂直方向）的横向屈曲位移变化曲线。试件屈曲的总横向位移则可按照矢量合成的原则进行计算，并可根据每一时刻两个正交方向的屈曲横向位移计算试件的屈曲方向。

按与文献[28]类似的方法对各试件进行编号，以“Y4-16-100-1”为例，“Y4”仍表示HRB400钢筋，“16” 表示钢筋直径D_s=16 mm，“100”表示试验开始时钢筋试件两夹持端之间的初始长度，即屈曲长度L_s=100 mm，“1”表示拉压相等循环加载试验。

2.2 試验结果及分析

试验结束后，对各钢筋试件的损伤特征进行全面分析，发现损伤主要集中在钢筋试件屈曲段中点附近，并造成钢筋在试件跨中断裂，试件Y4-16-150-1在试验结束后的损伤情况如图1所示。

试验过程中，各试件一般首先在屈曲钢筋跨中凹侧的月牙横肋附近出现裂缝，随着钢筋反复拉压并弯曲受力，该裂缝最终贯通钢筋的横截面（见图1（a））。少数钢筋在试件两端的夹持部位出现沿月牙肋分布的短裂缝，但在试验结束时该部位裂缝的宽度、深度仍很小（均不超过1.0 mm），远小于跨中部位的裂缝，可忽略其对试件低周疲劳寿命的影响（见图1（b））。

部分典型试件跨中截面的屈曲横向位移曲线如图2所示，图中的屈曲开始点按文献[30]的方法确定。

图2表明，各试件的屈曲横向位移（即屈曲钢筋的弯曲程度）随轴向加载位移?L_s的增加而逐渐加大，且横向屈曲位移较大之后，即使钢筋反向受拉，屈曲位移也不能再重新回到零，表明钢筋明显屈曲之后已难以再完全拉直。试件的长径比L_s?D_s 、屈服强度、加载方式不同时，钢筋的屈曲变形大小存在差异，且屈曲方向也不完全相同。一般情况下，随着长径比增大，试件的屈曲变形更大，其中试件Y4-16-192-2的最终屈曲变形小于试件Y4-16-150-2，原因是试件Y4-16-192-2提前断裂，即其最大轴向位移更小。各试件一般沿偏弱轴的斜方向屈曲，即弱轴方向测得的横向位移一般明显大于强轴方向的屈曲侧移，强轴方向的横向位移较小，故按矢量合成方法计算的总横向屈曲位移仅略大于弱轴方向的横向位移；与其他试件相比，试件Y4-16-150-1和Y4-16-192-1的弱轴横向位移相对更大，表明钢筋的屈曲方向存在一定的随机性。

各钢筋试件的平均应力-平均应变曲线（σ ?_s-ε ?_s）滞回曲线试验结果如图3和图4所示，图中的屈曲开始点仍按前述方法确定。HRB600钢筋的对应试验结果见文献[28]中图10～图15，此处不再重复列出。

图3、图4和文献[28]中图10～图15表明，钢筋强度相同时，L_s?D_s 越大，屈曲钢筋在受压时的强度、刚度退化越明显，即HRB400钢筋、HRB500钢筋和HRB600钢筋的滞回受力性能与长径比L_s?D_s 密切相关，这与Kunnath等[2]、Dhakal等[20]、Rodriguez等[22]、Monti等[23]和Gomes等[24]的研究结果相同；屈曲钢筋受拉时的强度退化远不如受压时明显，受拉强度退化主要与低周疲劳损伤引起的强度衰减有关[25]。另一方面，不同强度钢筋的受压强度和刚度退化程度、受拉强度衰减幅度也有区别，这与钢筋的材性差异有关。由于屈曲效应对各钢筋试件的强度衰减、刚度退化的影响规律不是本文的研究范围，此处不再赘述。

对比图3、图4和文献[28]中图10～图15的σ ?_s-ε ?_s滞回曲线可知，钢筋屈服强度f_y不同时，长径比相同的钢筋试件在断裂前能承受的循环加载总周数随f_y的提高而减少。需注意的是，钢筋长径比相同时，不同强度钢筋的弹性模量E_s差别很小，f_y大的试件屈服位移?L_sy=L_s ε_sy也更大，故各级加载位移?L_s以及对应的每一加载位移下的平均应变ε ?_s相应也更大。可见，分析试验结束时钢筋发生断裂的原因、影响因素时，既要考虑各级加载位移下最大平均应变ε ?_s的相对大小，也要考虑钢筋断裂前经历的总循环周数。合理的低周疲劳寿命模型可同时考虑平均应变幅、循环周数的影响，基于疲劳寿命模型能合理分析不同强度对屈曲钢筋损伤和断裂的影响。

2.3 循环受力屈曲钢筋的极限变形能力分析

为评估屈曲对钢筋在循环受力下的极限变形能力的影响，将各试件在试验过程中经历的受拉、受压的最大平均应变（见图3、图4和文献[28]中图10～图15）的绝对值相加，并将其定义为极限总平均应变ε ?_（s，ua，cyc）。根据试验结果可提取各试件的ε ?_（s，ua，cyc）数据，并绘制ε ?_（s，ua，cyc）-L_s?D_s 和ε ?_（s，ua，cyc）-f_y关系曲线，如图5和图6所示，据此可初步分析屈曲对钢筋在低周循环受力下变形能力的影响。

图5表明，即使对于L_s?D_s 较小的试件，其ε ?_（s，ua，cyc）也明显小于钢筋单调受拉时与钢筋断裂对应的极限拉应变ε_su（见表1）；随着长径比L_s?D_s 的增大，试件的极限总平均应变ε ?_（s，ua，cyc）整体上呈逐渐减小的规律，这说明试件的屈曲程度对循环加载下钢筋拉断的总应变有明显影响。事实上，可以从循环受力时钢筋低周疲劳损伤累积的角度定性分析图5的规律：由于钢筋试件的屈曲横向位移随L_s?D_s 的增大而加大（见图2），即L_s?D_s 越大，循环受力过程中钢筋的屈曲程度越严重，屈曲钢筋试件跨中关键弯曲部位的局部塑性变形集中现象也越显著，从而使其ε ?_（s，ua，cyc）一般更小。

图6表明，ε ?_（s，ua，cyc）随屈服强度f_y增大的变化方式与加载方式、长径比均有关，其规律较复杂。分析其原因，钢筋屈服强度f_y对ε ?_（s，ua，cyc）的影响方式较复杂， 如前所述，一方面与低周疲劳损伤有关，即长径比相同的钢筋试件，其断裂除与ε ?_（s，ua，cyc）有关外，循环周数（f_y大时循环周数少）也有影响。另一方面，f_y不同的钢筋，其材料性能除单调受力的极限拉应变ε_su不同外，抗拉强度f_u、与f_u对应的应变ε_sult也存在差异。上述两方面的原因导致f_y对ε ?_（s，ua，cyc）的影响规律较复杂。

总之，直接将单调受拉的ε_su与循环受力的极限总平均应变ε ?_（s，ua，cyc）进行比较，无法合理判断循环受力时钢筋的损伤和断裂情况。各研究者采用的方法均是根据低周疲劳寿命模型（应考虑屈曲效应的影响）计算钢筋在循环受力过程中的低周疲劳损伤指数D_f[21-28]，并根据D_f与1.0的关系判断钢筋是否断裂。

3 已有低周疲劳寿命模型的适用性分析

基于前述3种强度钢筋考虑屈曲的试验数据，对传统低周疲劳寿命模型（不考虑屈曲）、已有的可考虑屈曲效应的低周疲劳寿命模型的适用性进行评价。

3.1 传统低周疲劳寿命模型

如前所述，Coffin[10]和Manson[11]提出的经典C-M疲劳模型目前应用广泛，其表达式为

ε_sp=C_f  （2N_f ）^（-α） （1）

式中：εsp为未屈曲钢筋本循环周的塑性应变幅（见图7）；（2Nf ）为在εsp下按等幅加载直至失效（断裂）所需的半循环周数；Cf和α为疲劳参数。

经典C-M模型不考虑钢筋屈曲的影响，故图7中σ_s和ε_s分别为未屈曲钢筋的应力、应变；σ_0为第一循环周的最大正应力；ε_sa为本循环周的最大拉应变，ε_sa包括弹性、塑性两部分，故ε_sa也称为受拉总应变幅，即塑性应变幅ε_sp=ε_sa-ε_sy， ε_sy为钢筋的屈服应变。

3.2 考虑屈曲的已有低周疲劳寿命模型

可考虑钢筋屈曲效应的修正低周疲劳损伤模型很少。由于缺乏系统性试验结果，Kashani等[25]、Tripathi等[26]和杨红等[27-28]并未验证其建立的修正C-M模型用于不同强度钢筋的有效性。

因Tripathi等[26]建立的修正C-M模型是基于300E和500E两种强度的变形钢筋，以Tripathi等[26]的研究成果为例，分析其提出的修正C-M模型对中国生产的不同强度钢筋的适用性。Tripathi等[26]建立的修正C-M模型的数学表达式为

ε ?_sa=C_（f，Trp）  （2N_f ）^（-α_Trp ） （2）

C_（f，Trp）=0.2-λ?350 （3）

α_Trp=0.441+λ?（1 200） （4）

λ=（L_s?D_s ） 〖（f_y?100）〗^0.5 （5）

式中：ε ?_sa为屈曲钢筋在本循环周的最大平均拉应变；C_（f，Trp）和α_Trp为考虑屈曲影响的疲劳参数。

为了将考虑屈曲的修正C-M模型用于强烈地震作用下的柱纵筋断裂评估，在随机振幅循环加载中，可通过计算每一加载循环周的受拉总平均应变幅ε ?_sa （+）和受压总平均应变幅ε ?_sa （-）（如图8所示）以及对应的疲劳损伤指数D_（f i）（按式（6）计算），然后采用Miner线性损伤规则[31]（如式（7）所示）计算屈曲钢筋的累积低周疲劳损伤指数D_f [21， 32]。

D_（f i）=（ε ?_（sa i）/C_（f，Trp） ）^（-α_T rp）=1/（2N_f ）_i （6）

D_f=∑_（i=1）^n?D_（f i） =∑_（i=1）^n?（ε ?_（sa i）/C_（f，Trp） ） ^（-α_Trp ） （7）

式中：D_（f i）为第i半循环周的疲劳损伤指数；（2N_f ）_i为第i半循环周中与总平均应变幅ε ?_（sa i）对应的失效半循环周数（按ε ?_（sa i）加载至断裂所需半循环周数），其倒数即损伤指数D_（f i）。当D_f=1.0时，表示钢筋已断裂；当D_f=0时，代表钢筋无损伤。

3.3 已有低周疲劳寿命模型的有效性检验

基于HRB400钢筋、HRB500钢筋和HRB600钢筋的试验数据，对传统C-M疲劳模型（未考虑屈曲影响）、Tripathi等[26]的修正C-M模型（考虑屈曲影响）用于不同屈服强度钢筋的有效性进行检验。

首先检验传统C-M模型，其计算步骤如下：

1）张耀庭等[17]、吕品等[33]和孙传智等[19]分别基于HRB400钢筋、HRB500E钢筋和630 MPa级钢筋的高应变低周疲劳性能试验结果回归得到了关于式（1）的疲劳参数C_f和α取值，其中，HRB400钢筋取C_f=0.140和α=0.379[17]，HRB500钢筋取C_f=0.182和α=0.630 [32]，HRB600钢筋取C_f=0.259和α=0.449 [19]。对于考虑屈曲的试验，除将上述C_f和α取值代入式（1）外，还需将式（1）中的塑性应变幅ε_sp改写为ε ?_sp（塑性平均应变幅）。例如，HRB400钢筋的低周疲劳损伤指数D_（f i）按式（8）计算。

ε ?_sp=0.14（2N_f ）^（1/0.379） ， D_（f i）=（ε ?_（sp i）/0.14）^（1/0.379） （8）

2）根据Miner线性损伤规则[31]，对各试件均按式（6）计算每一半循环周的疲劳损伤指数D_（f i），再按式（7）计算累积疲劳损伤指数D_f，但应注意将式中的总平均应变幅ε ?_（sa i）转换为塑性平均应变幅ε ?_（sp i）。

采用传统C-M模型计算所得的D_f，结果如图9所示。由于试验结束时各试件均已断裂（即D_f=1.0），故将D_f的计算结果与1.0对比即可判断采用式（1）计算不同强度屈曲钢筋试件损伤程度的准确性。

C-M model

图9表明，采用未考虑屈曲的传统C-M疲劳寿命模型计算得到的3种强度的钢筋试件的D_f与屈曲钢筋的试验结果（D_f=1.0）差别很大，各试件的D_f分布具有较明显的规律性，即长径比（L_s?D_s ）小的试件，其D_f相对更接近1.0；随着L_s?D_s 的增大，D_f逐渐减小，其D_f与1.0的偏差也越来越大。可见，试件长径比越大，传统C-M模型越难预测在试验结束时3种强度钢筋试件跨中显著弯曲处已断裂的事实。

分析其原因，传统C-M模型是基于未屈曲钢筋的试验结果建立的，若直接采用式（1）进行计算，相当于将屈曲钢筋视为未弯曲且轴向拉压变形相同的试件，其实质是没有考虑屈曲钢筋跨中截面的局部塑性应变集中对疲劳损伤的不利影响[28]。由于试件的弯曲效应随L_s?D_s 的增大而越明显，屈曲导致的局部塑性应变集中和损伤增大也越显著，故长径比越大，采用传统C-M模型计算屈曲钢筋低周疲劳损伤的误差越显著[27-28]。

其次，验证Tripathi等[26]提出的修正C-M模型（考虑屈曲影响）用于中国生产的不同强度屈曲钢筋的有效性。其计算步骤如下：

1）将HRB400钢筋、HRB500钢筋的屈服强度（见表1）和HRB600钢筋的屈服强度（f_y=628.18 MPa，见文献[28]）和各钢筋试件的长径比L_s?D_s 代入式（5），计算各试件的参数λ=（L_s?D_s ） 〖（f_y?100）〗^0.5的取值。

2）根据各试件的λ计算结果，分别按式（3）和式（4）计算考虑屈曲影响的疲劳参数C_（f，Trp）和α_Trp的值。

3）按式（6）和式（7）计算各试件的D_f，即先根据式（6）计算每一半循环周的疲劳损伤指数D_（f i），然后按式（7）计算累积疲劳损伤指数D_f。

采用Tripathi等[26]的修正C-M模型進行计算得到的D_f如图10所示。

图10表明，基于300E、500 E钢筋试验结果建立的修正C-M疲劳模型虽然考虑了f_y和L_s?D_s 的影响，但将其用于计算中国生产的钢筋试件时，得到的D_f一般大于1.0，其中小长径比试件的误差很显著，而且该模型无法有效区分不同强度钢筋低周疲劳性能的差异，可见其并不适用于中国的钢筋。

分析其原因，新西兰生产的300E和500E变形钢筋的制作工艺、化学成分、微量元素等与中国相比存在差异，从而导致钢筋的材料性能与中国钢筋不同，例如，500E钢筋单调受拉时的极限应变ε_su=0.142（300E钢筋的ε_su=0.269）[26]，明显低于中国HRB500钢筋的极限变形能力（ε_su=19.400%，见表1）。

4 适用不同强度屈曲钢筋的疲劳模型修正

如前所述，考虑钢筋屈曲效应影响的修正低周疲劳损伤模型较少。Kashani等[25]和Tripathi等[26]均根据各自的屈曲钢筋试验结果，分别建立了基于总平均应变幅ε ?_sa的修正C-M模型。因此，笔者首先根据试验数据建立基于总平均应变幅ε ?_sa、可考虑屈曲影响的修正C-M低周疲劳损伤模型。

4.1 基于总平均应变幅ε ?_sa的修正模型

为了提高拟合效果，首先以HRB600钢筋的试验结果为例（其试件为16个，数量相对更多），基于ε ?_sa建立适用于HRB600钢筋、可考虑屈曲影响的修正低周疲劳寿命模型，其方法为：

1）在式（1）所示传统C-M模型中，采用总平均应变幅ε ?_sa代替其中的ε_sp。

2）对HRB600钢筋试件进行回归分析（即先暂不考虑f_y的影响），故式（1）的疲劳参数C_f和α均为长径比L_s?D_s 的函数。根据试验结果分别拟合C_f和α的计算方法。

3）基于HRB600钢筋的考虑屈曲的循环加载试验结果，对基于ε ?_sa的修正C-M模型中的疲劳参数（C_f和α）进行回归分析，即可得到修正后的C-M模型。

综上，式（1）可改写为

ε ?_sa=C_（f，ma） （L_s?D_s ） （2N_f ）^（-α_ma （L_s?D_s ）） （9）

在式（9）中，疲劳材料参数C_（f，ma） （L_s?D_s ）、疲劳指数α_ma （L_s?D_s ）均为与长径比L_s?D_s 有关的变量，即式（9）通过C_（f，ma） （L_s?D_s ）和α_ma （L_s?D_s ）这两个变量考虑长径比对屈曲钢筋低周疲劳损伤的影响。

根据考虑屈曲的循环加载试验结果，提取各HRB600钢筋试件在每一加载循环的ε ?_（sa i），按式（6）计算D_（f i），然后以试验结束时D_f=1.0为目标函数，分别对式（9）中的参数进行拟合，可得到适用于HRB600钢筋的C_（f，ma） （L_s?D_s ）和α_ma （L_s?D_s ）的计算公式。

C_（f，ma）=21.86（L_s?D_s ）^（-3.114）+0.12 （10）

α_ma=-8.076（L_s?D_s ）^（-2.54）+0.46 （11）

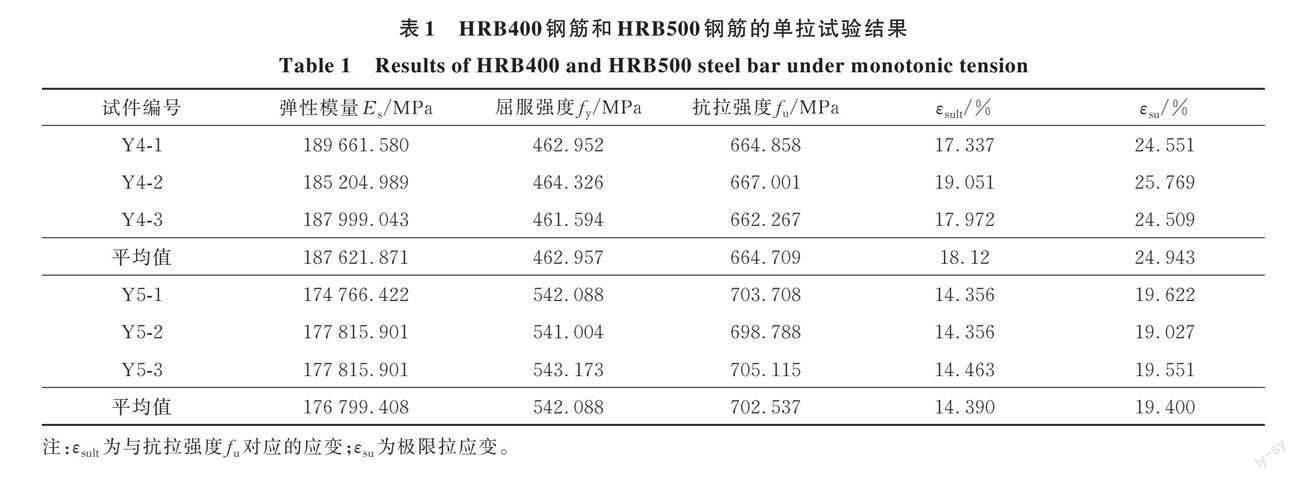
式（10）和式（11）的拟合效果如图11所示，可见其拟合精度较理想。

采用基于ε ?_sa的修正C-M模型（如式（9）～（11）所示）计算HRB600钢筋试件的累积低周疲劳损伤指数D_f，结果如图12所示。

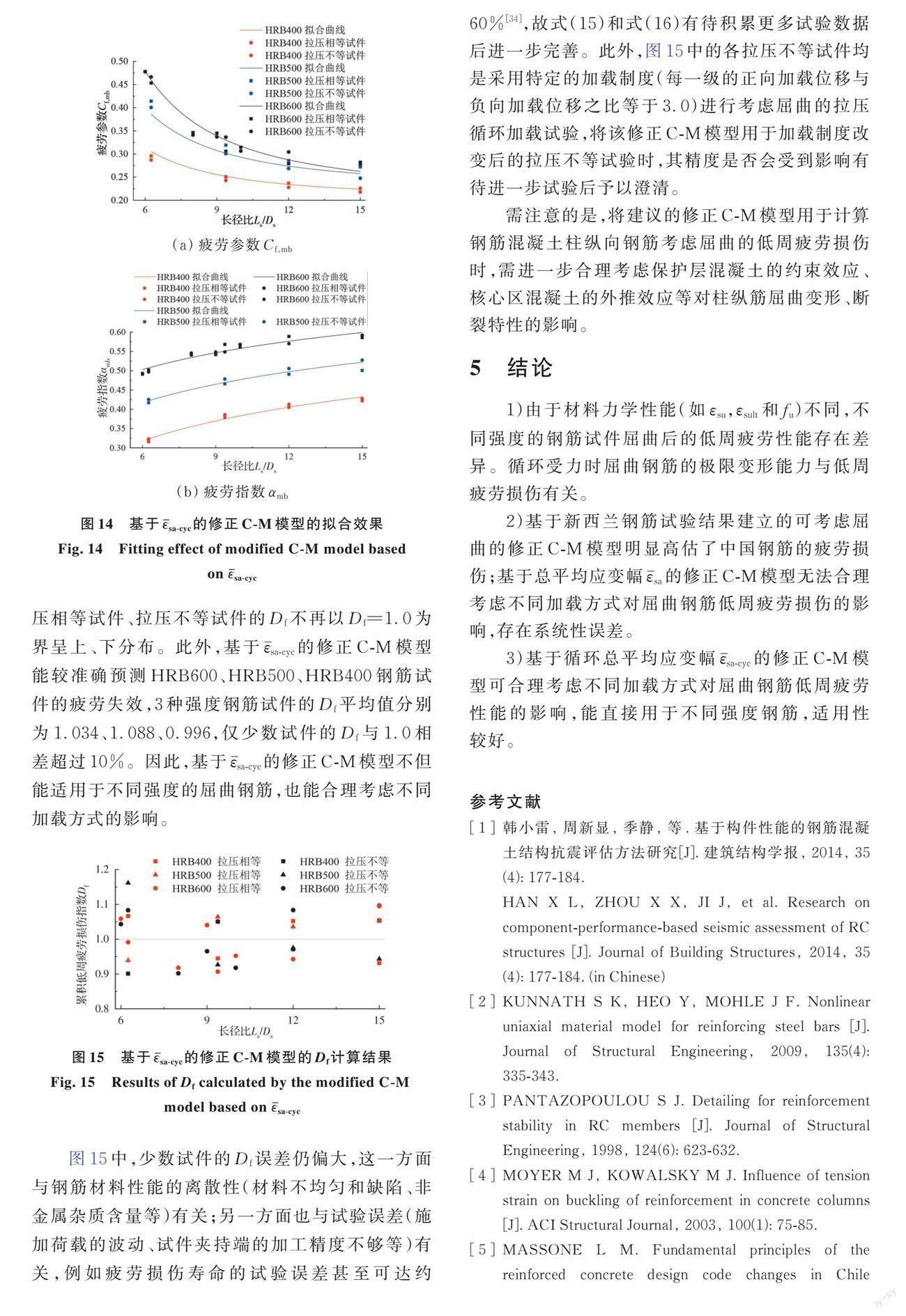
与图9所示D_f结果相比，图12中D_f总体上明显更接近1.0，误差更小，可见基于ε ?_sa的修正C-M模型改善效果明显。但仔细观察图12可发现，其存在明显缺陷，即计算得到的拉压相等试件的D_f值一般小于1.0、拉压不等试件的D_f值一般大于1.0，即以D_f=1.0为界，两种加载方式的钢筋试件的D_f值呈明显的上、下分布。可见，基于ε ?_sa的修正C-M疲劳模型计算的D_f存在系统性误差。

分析这一现象，该系统误差主要是由于加载方式不同，使得这两类试件的受拉ε ?_sa、受压ε ?_sa均存在明显差异所致。具体而言，拉压相等试件每一级位移幅值为3?L_sy的整数倍；拉压不等试件每一级位移幅值分别为4.5?L_sy和-1.5 ?L_sy的整数倍。因此，每一级位移幅值下，两种加载方式钢筋试件的受拉ε ?_sa、受压ε ?_sa的绝对值之和是相等的；但是很显然，拉压不等试件的受拉ε ?_sa更大、受压ε ?_sa更小（拉压相等试件的受拉ε ?_sa、受压ε ?_sa的绝对值相等）。对于L_s?D_s 和f_y相同的试件，两种加载方式下钢筋试件按照回归公式计算得到的疲劳参数C_（f，ma） （L_s?D_s ）和α_ma （L_s?D_s ）的值必然相同，将其代入式（6）计算第i半循环周的疲劳损伤指数D_（f i）时，拉压不等试件受拉ε ?_sa更大的现象会导致其D_（f i）的计算结果也相应更大（与拉压相等试件相比），即其受拉ε ?_sa与拉压相等试件的受拉ε ?_sa之间的差异会被α_ma （L_s?D_s ）以指数的方式放大。这种差异在各半循环周均存在，故拉压不等试件累计后的D_f值必然更大，从而形成以D_f=1.0为界呈上、下分布的现象。

由于存在这种系统性误差，基于总平均应变幅ε ?_sa的修正C-M模型仅适用于特定加载方式下屈曲钢筋的疲劳损伤计算，无法将其用于强烈地震作用下的柱纵筋断裂评估。

因此，基于总平均应变幅ε ?_sa建立的修正C-M模型的主要缺点是，难以正确描述不同加载方式（如拉压不等加载、拉压相等加载）的损伤规律。Kashani等[25]和Tripathi等[26]仅依据拉压相等加载的试验结果对其提出的修正C-M疲劳模型进行校核，自然无法发现这一系统性误差对其改进模型的影响。

4.2 基于循环总平均应变幅ε ?sa-cyc的修正模型

基于总平均应变幅ε ?_sa的修正C-M模型無法考虑不同加载方式对屈曲钢筋低周疲劳寿命模型的影响，存在系统性误差。杨红等[28]的研究结果表明，基于循环总平均应变ε ?sa-cyc的修正C-M模型能合理考虑不同加载方式的影响，较准确地判断HRB600钢筋的损伤和断裂情况，但不足之处是，其提出的基于ε ?sa-cyc的修正C-M模型是仅基于HRB600钢筋的试验结果建立的，即仅考虑了长径比对参数C_f和α的影响，该模型无法用于其他强度钢筋。

为提出可考虑屈曲影响、适用于不同强度钢筋、可合理考虑不同加载方式影响的修正C-M低周疲劳寿命模型，提出以下基于ε ?sa-cyc的修正C-M模型。

1）采用循环总平均应变幅ε ?sa-cyc代替式（1）中的ε_sp，ε ?sa-cyc的定义如图13所示，其中ε ?sa-cyc（+）和ε ?sa-cyc（-）分别为受拉、受压半循环周的循环总平均应变幅。屈曲钢筋受拉时，ε ?sa-cyc（+）=ε ?_sa （+）+|ε ?_s0 （-）|，即ε ?sa-cyc（+）等于本循环周受拉的总平均应变幅ε ?_sa （+）与上一循环周受压的残余平均应变ε ?_s0 （-）的绝对值之和；屈曲钢筋受压时，ε ?sa-cyc（-）=|ε ?_sa （-）|+ε ?_s0 （+），其计算方法与受拉时类似。

2）研究结果表明[20-28]，钢筋的屈曲受力性能主要与L_s?D_s 和f_y有关。故仍采用Dhakal等[20]建议的无量纲屈曲性能参数λ=（L_s?D_s ） 〖（f_y?100）〗^0.5同时考虑长径比、屈服强度对屈曲钢筋疲劳受力性能的影响，此时，式（1）应修正为式（12）的形式，其中的疲劳参数C_（f，mb）和α_mb的计算方法需根据试验结果进行拟合。

ε ?sa-cyc=C_（f，mb）  （2N_f ）^（-α_mb ） （12）

式中：疲劳材料参数C_（f，mb）、疲劳指数α_mb均是与λ、f_y有关的变量。可见，基于ε ?sa-cyc的修正C-M模型可通过C_（f，mb）和α_mb同时考虑长径比L_s?D_s 、屈服強度f_y对屈曲钢筋低周疲劳损伤的影响。

3）基于3种强度钢筋试件考虑屈曲的循环加载试验的试验结果，在各试件的每一加载循环中，分别提取受拉半循环周的ε ?_（sa i） （+）和ε ?_（s0 i） （-）、受压半循环周的ε ?_（sa i） （-）和ε ?_（s0 i） （+），计算相应的循环总平均应变幅ε ?sa-cyc（+）和ε ?sa-cyc（-）。然后根据Miner线性损伤规则[31]，按式（13）计算每一半循环周的疲劳损伤指数D_（f i），并按式（14）计算各试件的累积疲劳损伤指数D_f。

D_（f i）=1/（2N_f ）_i =（ε ?_（sa?cyc i）/（C_（f，mb） （λ）））^（-α_mb （λ）） （13）

D_f=∑_（i=1）^n?D_（f i） =∑_（i=1）^n?（ε ?_（sa?cyc i）/（C_（f，mb） （λ））） ^（-α_mb （λ）） （14）

4）回归分析时，仍以试验结束时D_f=1.0为目标函数，但同时考虑3种强度钢筋试件的试验结果和提取的数据，对式（12）进行拟合，可得到同时适用于3种强度钢筋的新材料参数C_（f，mb）、新疲劳指数α_mb的计算公式，如式（15）、式（16）所示。

C_（f，mb）=0.036〖（f_y?100）〗^1.907 （λ）^（-1.849）+0.214   （15）

α_mb=-3.393〖（f_y?100）〗^0.256 （λ）^（-0.113）+1.48   （16）

式（15）和式（16）的拟合效果如图14所示。

采用基于ε ?sa-cyc的修正C-M模型对3种强度钢筋试件的累积低周疲劳损伤指数D_f进行计算，即将各试件的参数λ、f_y代入式（15）和式（16），计算C_（f，mb）和α_mb的取值，再根据式（13）和式（14）计算累积低周疲劳损伤指数D_f，结果如图15所示。

图15表明，基于ε ?sa-cyc的修正C-M模型能够有效消除基于ε ?_sa的修正C-M模型带来的系统性误差，拉压相等试件、拉压不等试件的D_f不再以D_f=1.0为界呈上、下分布。此外，基于ε ?sa-cyc的修正C-M模型能较准确预测HRB600、HRB500、HRB400钢筋试件的疲劳失效，3种强度钢筋试件的D_f平均值分别为1.034、1.088、0.996，仅少数试件的D_f与1.0相差超过10%。因此，基于ε ?sa-cyc的修正C-M模型不但能适用于不同强度的屈曲钢筋，也能合理考虑不同加载方式的影响。

图15中，少数试件的D_f误差仍偏大，这一方面与钢筋材料性能的离散性（材料不均匀和缺陷、非金属杂质含量等）有关；另一方面也与试验误差（施加荷载的波动、试件夹持端的加工精度不够等）有关，例如疲劳损伤寿命的试验误差甚至可达约60%[34]，故式（15）和式（16）有待积累更多试验数据后进一步完善。此外，图15中的各拉压不等试件均是采用特定的加载制度（每一级的正向加载位移与负向加载位移之比等于3.0）进行考虑屈曲的拉压循环加载试验，将该修正C-M模型用于加载制度改变后的拉压不等试验时，其精度是否会受到影响有待进一步试验后予以澄清。

需注意的是，将建议的修正C-M模型用于计算钢筋混凝土柱纵向钢筋考虑屈曲的低周疲劳损伤时，需进一步合理考虑保护层混凝土的约束效应、核心区混凝土的外推效应等对柱纵筋屈曲变形、断裂特性的影响。

5 结论

1）由于材料力学性能（如ε_su，ε_sult和f_u）不同，不同强度的钢筋试件屈曲后的低周疲劳性能存在差异。循环受力时屈曲钢筋的极限变形能力与低周疲劳损伤有关。

2）基于新西兰钢筋试验结果建立的可考虑屈曲的修正C-M模型明显高估了中国钢筋的疲劳损伤；基于总平均应变幅ε ?_sa的修正C-M模型无法合理考虑不同加载方式对屈曲钢筋低周疲劳损伤的影响，存在系统性误差。

3）基于循环总平均应变幅ε ?sa-cyc的修正C-M模型可合理考虑不同加载方式对屈曲钢筋低周疲劳性能的影响，能直接用于不同强度钢筋，适用性较好。

參考文献

[1]  韩小雷， 周新显， 季静， 等. 基于构件性能的钢筋混凝土结构抗震评估方法研究[J]. 建筑结构学报， 2014， 35（4）： 177-184.

HAN X L， ZHOU X X， JI J， et al. Research on component-performance-based seismic assessment of RC structures [J]. Journal of Building Structures， 2014， 35（4）： 177-184. （in Chinese）

[2]  KUNNATH S K， HEO Y， MOHLE J F. Nonlinear uniaxial material model for reinforcing steel bars [J]. Journal of Structural Engineering， 2009， 135（4）： 335-343.

[3]  PANTAZOPOULOU S J. Detailing for reinforcement stability in RC members [J]. Journal of Structural Engineering， 1998， 124（6）： 623-632.

[4]  MOYER M J， KOWALSKY M J. Influence of tension strain on buckling of reinforcement in concrete columns [J]. ACI Structural Journal， 2003， 100（1）： 75-85.

[5]  MASSONE L M. Fundamental principles of the reinforced concrete design code changes in Chile following the Mw 8.8 earthquake in 2010 [J]. Engineering Structures， 2013， 56： 1335-1345.

[6]  YANG H， SUN P X， DENG Y J. Experiment investigation of the influence of reinforcing bar buckling on seismic behavior of RC columns [J]. Engineering Structures， 2020， 220： 110923.

[7]  BROWN W A， LEHMAN D E， STANTON J F. Bar buckling in reinforced concrete bridge columns： PEER Report 2007/11 [R]. PEER Center， Berkeley， CA， 2008.

[8]  SU J S， WANG J J， BAI Z Z， et al. Influence of reinforcement buckling on the seismic performance of reinforced concrete columns [J]. Engineering Structures， 2015， 103： 174-188.

[9]  EL-BAHY A， KUNNATH S K， STONE W C， et al. Cumulative seismic damage of circular bridge columns： Benchmark and low-cycle fatigue tests [J]. ACI Structural Journal， 1999， 96（4）： 633-641.

[10]  COFFIN L. A study of the effects of cyclic thermal stresses on a ductile metal [J]. American Society of Mechanical Engineers， 1954， 76： 931-950.

[11]  MANSON S S. Behavior of materials under conditions of thermal stress [R]. Heat Transfer Symposium， University of Michigan Engineering Research Institute， Ann Arbor， Michigan， 1953.

[12]  WANG M L， SHAH S P. Reinforced concrete hysteresis model based on the damage concept [J]. Mathematical and Computer Modelling， 1989， 12（3）： 377-378.

[13]  KOH S K， STEPHENS R I. Mean stress effects on low cycle fatigue for a high strength steel [J]. Fatigue & Fracture of Engineering Materials and Structures， 1991， 14（4）： 413-428.

[14]  MCCABE S L， HALL W J. Assessment of seismic structural damage [J]. Journal of Structural Engineering， 1989， 115（9）： 2166-2183.

[15]  MANDER J B， PANTHAKI F D， KASALANATI A. Low-cycle fatigue behavior of reinforcing steel [J]. Journal of Materials in Civil Engineering， 1994， 6（4）： 453-468.

[16]  HAWILEH R A， ABDALLA J A， OUDAH F， et al. Low-cycle fatigue life behaviour of BS 460B and BS B500B steel reinforcing bars [J]. Fatigue & Fracture of Engineering Materials & Structures， 2010， 33（7）： 397-407.

[17]  張耀庭， 赵璧归， 李瑞鸽， 等. HRB400钢筋单调拉伸及低周疲劳性能试验研究[J]. 工程力学， 2016， 33（4）： 121-129.

ZHANG Y T， ZHAO B G， LI R G， et al. Monotonic and low cycle fatigue testing and research for HRB400 steel [J]. Engineering Mechanics， 2016， 33（4）： 121-129. （in Chinese）

[18]  郑家良， 盛光敏， 王丽鹃， 等. HRB500E钢筋高应变低周疲劳性能研究[J]. 钢铁钒钛， 2014， 35（5）： 129-135.

ZHENG J L， SHENG G M， WANG L J， et al. Investigation of high strain and low cycle fatigue behaviors for HRB500E rebars [J]. Iron Steel Vanadium Titanium， 2014， 35（5）： 129-135. （in Chinese）

[19]  孙传智， 缪长青， 李爱群， 等. 630 MPa超高强钢筋低周疲劳性能试验研究[J]. 建筑结构学报， 2021， 42（4）： 194-202.

SUN C Z， MIAO C Q， LI A Q， et al. Experimental study on low cycle fatigue properties of 630 MPa super-high strength steel bar [J]. Journal of Building Structures， 2021， 42（4）： 194-202. （in Chinese）

[20]  DHAKAL R P， MAEKAWA K. Modeling for postyield buckling of reinforcement [J]. Journal of Structural Engineering， 2002， 128（9）： 1139-1147.

[21]  KUNNATH S K， KANVINDE A， XIAO Y， et al. Effects of buckling and low cycle fatigue on seismic performance of reinforcing bars and mechanical couplers for critical structural members： A technical report submitted to the California Department of Transportation under Contract 59A0539 [R]. Davis， California， USA： University of California at Davis， 2009.

[22]  RODRIGUEZ M E， BOTERO J C， VILLA J. Cyclic stress-strain behavior of reinforcing steel including effect of buckling [J]. Journal of Structural Engineering， 1999， 125（6）： 605-612.

[23]  MONTI G， NUTI C. Nonlinear cyclic behavior of reinforcing bars including buckling [J]. Journal of Structural Engineering， 1992， 118（12）： 3268-3284.

[24]  GOMES A， APPLETON J. Nonlinear cyclic stress-strain relationship of reinforcing bars including buckling [J]. Engineering Structures， 1997， 19（10）： 822-826.

[25]  KASHANI M M， BARMI A K， MALINOVA V S. Influence of inelastic buckling on low-cycle fatigue degradation of reinforcing bars [J]. Construction and Building Materials， 2015， 94： 644-655.

[26]  TRIPATHI M， DHAKAL R P， DASHTI F， et al. Low-cycle fatigue behaviour of reinforcing bars including the effect of inelastic buckling [J]. Construction and Building Materials， 2018， 190： 1226-1235.

[27]  杨红， 冉小峰， 谢琴. 考虑屈曲效应的混凝土柱纵筋低周疲劳性能和变形能力研究[J]. 建筑结构学报， 2021， 42（3）： 102-113.

YANG H， RAN X F， XIE Q. Study on low-cycle fatigue behavior and deformation capacity of longitudinal steel bar in RC columns considering effect of buckling [J]. Journal of Building Structures， 2021， 42（3）： 102-113. （in Chinese）

[28]  杨红， 蒋惠， 冉小峰. HRB600钢筋屈曲受力性能试验研究[J]. 工程力学， 2022， 39（6）： 83-98.

YANG H， JIANG H， RAN X F. Experimental research on the buckling behavior of HRB600 steel bars [J]. Engineering Mechanics， 2022， 39（6）： 83-98. （in Chinese）

[29]  钢筋混凝土用钢 第2部分：热轧带肋钢筋： GB/T 1499.2—2018 [S] 北京： 中国标准出版社， 2018.

Steel for the reinforcement of concrete-Part 2： Hot rolled ribbed bars： GB/T 1499.2—2018 [S]. Beijing： Standards Press of China， 2018. （in Chinese）

[30]  劉子珅， 杨红， 张吉庆. 基于横向挠度的钢筋屈曲状态判断方法研究[J]. 工程力学， 2018， 35（2）： 144-152.

LIU Z S， YANG H， ZHANG J Q. Research on buckling state determination of reinforcing bars based on lateral deflection [J]. Engineering Mechanics， 2018， 35（2）： 144-152. （in Chinese）

[31]  MINER M A. Cumulative damage in fatigue [J]. Journal of Applied Mechanics， 1945， 12（3）： 159-164.

[32]  BROWN J， KUNNATH S K. Low-cycle fatigue failure of reinforcing steel bars [J]. ACI Materials Journal， 2004， 101（6）： 457-466.

[33]  吕品. HRB500高强钢筋低周疲劳性能研究[D]. 辽宁 大连： 大连理工大学， 2011.

LV P. Research on low cycle fatigue behavior of high strength steel HRB500 [D]. Dalian， Liaoning： Dalian University of Technology， 2011. （in Chinese）

[34]  薛昊飞. 钢筋高应变低周疲劳寿命的统计分析及钒微合金化的影响[D]. 重庆： 重庆大学， 2012： 21-50.

XUE H F. Statistical analysis of high strain and low cycle fatigue life of rebars and the effect of vanadium microalloying [D]. Chongqing： Chongqing University， 2012： 21-50. （in Chinese）

（编辑  王秀玲）