基于摩擦起电原理的悬臂—质量块式发电机研究

孔德娟,诸立锋,郭慧芳

(1.浙江同济科技职业学院,浙江 杭州 311231; 2.浙江大学,浙江 杭州 310027; 3.杭州福斯达深冷装备股份有限公司,浙江 杭州 311100)

在当前化石能源日益紧缺的情况下,发展高效的清洁能源材料与先进的能源收集技术成为了人类应对能源危机、实现可持续发展的2个重要措施。众所周知,在人们身边“游荡”着各种形式的机械能,如风能、海洋波浪能、火车或汽车运行引起的铁轨/公路地基的振动。如果对这些“游荡”的机械能加以收集利用,无疑将有助于缓解人类所面临的能源短缺问题。然而,在很多情况下,这些机械能大都以较低的能量密度和较低的频率频范围存在[1-2]。因此,传统的能量收集技术,例如基于压电结构和电磁感应的能量收集技术都不太适合。

基于摩擦起电原理的摩擦纳米发电机(简称“TENG”)是由王中林教授课题组最早提出的[3]。它主要是,利用特殊设计的结构单元,在环境机械能作用下发生运动时所产生的摩擦或接触静电,将环境中的机械能转化为电能。TENG技术尤其适用于低频振动的能量收集,已经被应用在人体运动产生的微弱机械能收集[4-6]、波浪能收集[7-10]、风能收集[11-13]等方面。需要指出的是:由于TENG是把环境中的机械能转换成电能,它所产生的电信号在本质上也体现了环境中产生机械能对象的振动或运动状态;因此,TENG本身也是一种具有自供电性能的传感器,已被用于运动传感[14-16]和振动传感[17-18]等方面。

基于摩擦起电原理的TENG技术,不仅取决于环境激励源的振动频率和振幅,还依赖于TENG发电单元的界面的有效接触面积。通常情况下,环境中振动激励源的频率和振幅是在一定范围内变化的,而有效接触面积通常取决于2个界面的表面属性和接触过程产生的弹性形变。人们已经通过镀纳米颗粒[19]、刻蚀与光刻技术[20]等方式加工摩擦层,改变其表面粗糙度,以提高界面的有效接触面积进而提高TENG的输出性能。但是,对于适用于环境激励源频率变化情况下的TENG发电技术和表面属性如何影响到TENG输出性能这两个方面的研究,还很匮乏;尤其是,在已建立的TENG理论模型中,几乎都没有考虑界面接触时产生的弹性形变的影响。

本文提出一种基于空腔—悬臂梁质量块的频率可调的TENG发电结构,简记为“CCM-TENG结构”,它主要由空腔基底、内置悬臂梁和端部弹性质量块构成。在受到外界振动激励时,悬臂梁发生弯曲振动并驱使末端弹性质量块在竖直方向作周期运动、进而与空腔上下的电极接触而产生感应电荷。基于产生的感应电荷,不仅可以用于检测外界激励状态,还可以用于能量收集。本文提出的CCM-TENG发电单元具有结构简单、频率可调的优点,可适用于收集海洋、湖泊等复杂水域的波浪能和交通道路中的振动能以及其他工程环境中“游荡”的机械能等。针对CCM-TENG结构,给出了综合考虑悬臂梁、质量块弹性形变及其表面粗糙度的理论分析模型,并实验测量了该CCM-TENG发电结构的输出性能。

1 CCM-TENG结构及工作原理

CCM-TENG发电结构如图1所示,由空腔基底、悬臂梁和端部弹性质量块组成。悬臂梁为玻璃纤维材料,质量块用极对称性的硅胶弹性球,基底由PLA材料通过3D打印得到(填充率为20%),空腔基底内部的上下壁面为铜电极。基于悬臂梁—球式结构的TENG发电单元的工作原理如图2所示,在环境振动激励下基底与悬臂梁结构发生相对运动,使悬臂梁发生受迫振动;其端部的弹性球随悬臂梁运动而接触上下铜电极。弹性球与上下铜电极发生周期性的弹性接触,进而产生周期性的感应电荷。由图2可知,当弹性球从a状态到b状态时,上壁面的正电荷不断增加,此时上壁面电极的电子会从外电路流向下壁面电极;当弹性球从b状态运动至c状态时,电子从下壁面通过外电路流向上壁面;弹性球处于c状态时,上下壁面电荷量一致,此时外电路没有发生电荷转移;当弹性球从c状态运动至d状态时,电子从下壁面通过外电路流向上壁面。于是,弹性球振动的这四个状态与输出电荷可以对应起来。注意:实际中,悬臂梁—球式结构有2种工作模式——非接触式和接触式。非接触模式是弹性球不与上下电极接触的情况。接触式是指弹性球与上下电极接触的情况,而本文也只考虑此种情况。

图1 CCM-TENG结构示意Fig.1 Schematic diagram of CCM-TENG structure

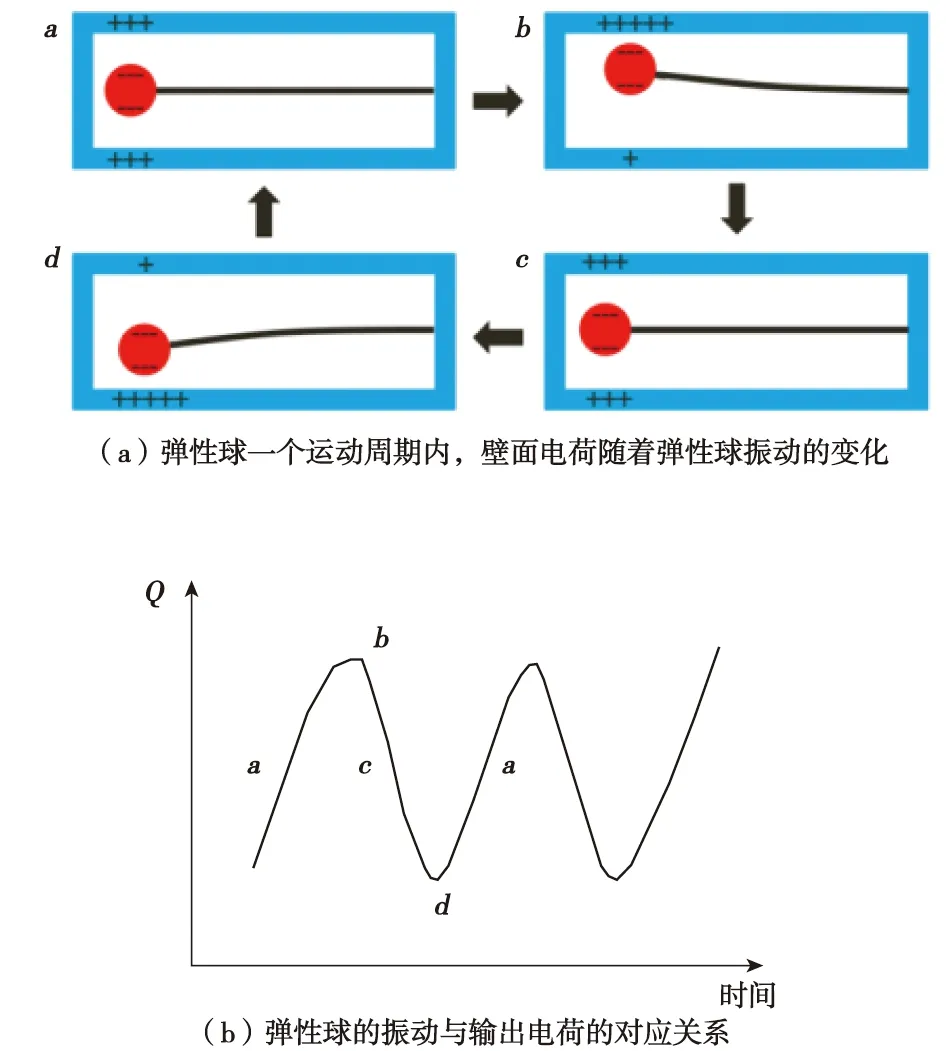
图2 CCM-TENG工作原理Fig.2 Working principle of CCM-TENG

2 CCM-TENG理论分析模型

针对图1所示的CCM-TENG结构,建立相应的理论分析模型。记弹性球的半径为r,密度为ρ,质量m=4πr3ρ,弹性模量为E,泊松比为μ;悬臂梁的长度为L、惯性矩为I、弹性模量为EL;PLA空腔基底高度为l。对于本文实验中使用的硅胶球和PLA空腔基底来说,在硅胶球与贴有铜电极的PLA接触过程中,可把空腔基底看做刚体而不发生弹性形变。考虑悬臂梁发生小挠度的情况,悬臂梁端部球的运动可等效为一弹簧—质量系统的运动,其等效弹簧系数为k=3ELI/L3。设系统的阻尼系数为c。当支座处有周期性位移激励(y=Ysinωt)时,弹性球做受迫振动的运动方程可写为:

(1)

式中,x为弹性球的位移。

对于受迫振动问题,只需求方程(1)的特解。设方程(1)的特解为:

x=Xsin(ωt-φ)

(2)

式中,φ=arctan [mcω2/(k2-mkω2+c2ω2)]为相位。把式(2)代入式(1)可得:

(3)

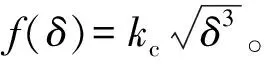
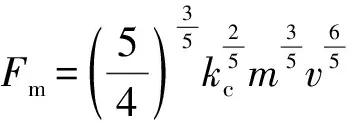
(4)

由式(2)可得弹性球在空腔中的速度:

v(t)=Xωcos(ωt-φ)

(5)

当弹性球与壁面接触时,即弹性球的位移为l/2,此时弹性球的速度为:

(6)

将式(3)、式(6)代入式(4)可得:

Fm=

(7)

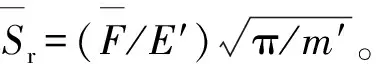
(8)

于是,弹性球与壁面接触时的最大接触电荷量为Qm=σrSr,其中σr为弹性球与电极接触的饱和电荷密度。由式(7)和式(8)可得:

(9)

进一步,可得CCM-TENG发电结构的输出电流峰值为Im=Qmω为:

(10)

由式(9)和(10)可知,图1中CCM-TENG发电结构的输出电荷和电流依赖于激励的频率、幅值、悬臂梁和弹性球的材料与几何参数以及弹性球的表面粗糙度。调整悬臂梁长度和质量块使系统固有频率与激励频率接近,可利用共振机制使CCM-TENG发电结构有较大的输出性能。此外,由于均方根斜率是表征表面粗糙度的参数,其值的减小能提高输出电荷。因此,可以对弹性球进行表面处理(如表面镀纳米颗粒),以降低表面粗糙度来增大实际接触面积,提高CCM-TENG发电结构的输出性能。

3 实验设计

实验采用的悬臂梁—球式单元构成的CCM-TENG发电结构如图3(a)所示,实验模型下半部分可用来改变悬臂梁长度,以实现调节系统固有频率,进而实现适应环境激励频率。实验中,硅胶球大小均相同,空腔上下壁面相距20 mm。实验中用到的主要常规设备有:信号发生器、功率放大器、激振器、Keithley6517高阻表等。为防止实验室中的工频干扰,所有实验测试均在静电屏蔽罩内完成。激振器与试验模型正中心位置给予位移激励如图3(b)所示,把制备的TENG结构放置在激振器上方,通过信号发生器设定激振频率,采用功率放大器调节振幅,激振器会输出设定的位移激励给空腔基底,从而使内部悬臂梁—弹性球结构发生弯曲振动。振动过程中产生的摩擦电信号由Keithley6517b高阻表记录。

图3 实验模型与实验装置Fig.3 Experimental model and equipment

4 结果与分析

对于长为L、弹性模量为EL、惯性矩为I、端部弹性球质量为m的悬臂梁系统,其固有频率为

(11)

实验中悬臂梁材质为玻璃纤维、弹性模量为80 GPa,长度为42 mm,横截面直径为1 mm;弹性球的直径为15 mm,质量为2.06 g。由式(11)可得其理论固有频率为44.2 Hz。实验中将6个悬臂梁—球式结构串联。给定振幅(0.227 3 mm)下,激励频率分别为40、50、60和70 Hz时的输出电信号波形如图4所示。

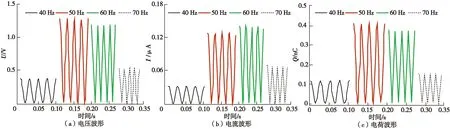
图4 不同频率下的电信号波形,激励振幅为0.227 3 mmFig.4 Waveforms of electrical signals at different frequencies,with an excitation amplitude of 0.227 3 mm

由图4可知,在给定振幅下,电压、电流和电荷在50、60 Hz附近有较大的输出信号。悬臂梁—球式结构的固有频率为44.2 Hz,除去实验测量误差后,悬臂梁—球式结构的共振频率有可能存在40～70 Hz。可以通过调节悬臂梁—球式结构的参数,使其共振频率处于环境振动的频率范围内,加强其输出信号。

为了验证理论模型(即式(10)和式(11))的可靠性,实验测量了激励频率为40 Hz下不同振幅的输出电信号,并与忽略阻尼影响的理论结果对比如图5所示。由图5可知,随着激励振幅的增加,其输出电信号峰值也会随之增加;实验与理论结果在数量级上一致,变化趋势也相近,这说明所构建的理论模型有一定的可靠性。此外,实验中还测量了悬臂梁的长度、弹性球直径和弹性球个数对输出性能的影响,如图6所示。

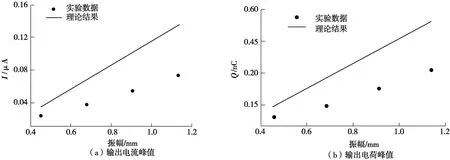
图5 不同振幅下实验与理论结果Fig.5 Experimental and theoretical results at different amplitudes

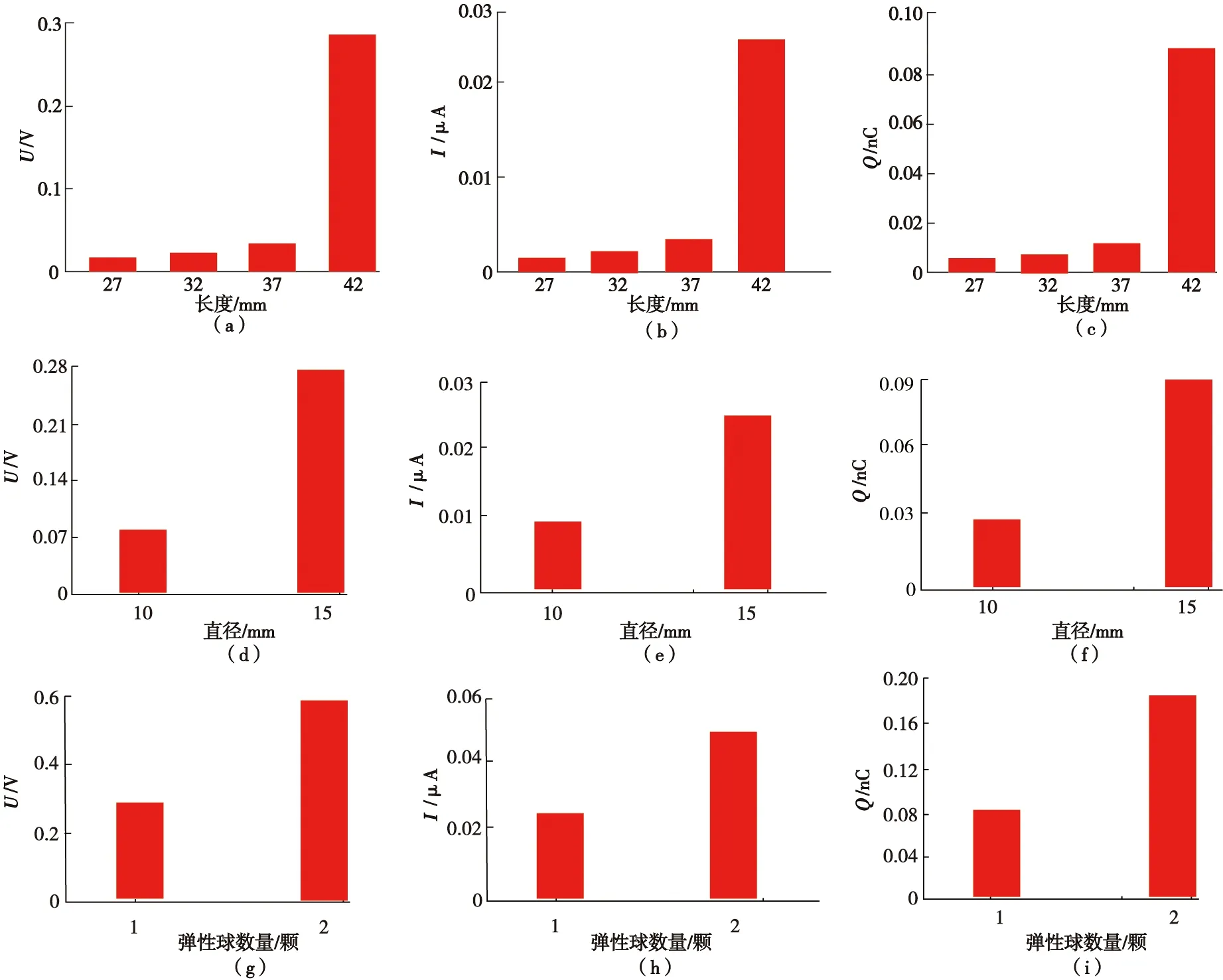
图6 在相同激励情况下不同情况的电压、电流、电荷峰值Fig.6 Under the same excitation conditions the voltage,current,and charge peaks under different conditions

图6(a)、(b)和(c)为频率40 Hz、振幅0.454 6 mm激励下,弹性球直径为15 mm,悬臂梁长分别为27、32、37、42 mm时的电信号峰值。可以看到,随着悬臂梁长度的增加,悬臂梁—球式结构的等效弹簧系数减小,悬臂梁末端挠度随之增加,从而使输出信号增加。图6(d)、(e)和(f)为在相同激励下,悬臂梁长度为42 mm时,弹性球直径分别为10、15 mm情况下的电信号峰值。由图6可知,随弹性球直径增加,系统输出信号增大,这是因为接触面积增加的缘故。图6(g)、(h)和(i)为相同激励下,悬臂梁末端分别带有1个与2个弹性球情况下的电信号峰值。由图6可知,悬臂梁末端有两颗弹性球时,其输出信号大约为1颗弹性球时的2倍。因此,该俘能器可通过调节悬臂梁长度、弹性球直径以及悬臂梁末端的弹性球数量来改进其输出性能,悬臂梁越长,弹性球直径越大,悬臂梁上末端弹性球越多,其输出性能越高。

5 结论

本文提出了一种基于空腔—悬臂梁质量块式的发电结构(CCM-TENG),它具有结构简单和频率可调的特征、适用于复杂环境下的机械能收集。考虑弹性球的机械变形及其表面粗糙度,基于经典Hertz接触模型并构建了预测CCM-TENG发电性能的理论模型。导出的输出电荷与输出电流的解析表达式中包含了激励频率、激励振幅,悬臂梁结构的几何和材料参数,弹性球几何及其表面粗造度等关键设计参数。进一步,实验测量了CCM-TENG在不同参数和不同激励下的性能。实验结果表明,当激励频率处于CCM-TENG结构固有频率附近,其具有较大的能量输出,增加梁长和弹性球的直径均能使CCM-TENG发电结构的输出性能得到提升。此外,对于输出电荷与电流,理论结果与实验结果吻合较好,这说明所构建的理论分析模型是可靠的。本文结果为基于空腔—悬臂梁质量块式TENG发电机的开发与应用提供了理论指导。