全长黏结锚杆特征荷载试验研究

江 冠，冯忠居，赵瑞欣，王富春，王思琦

(1. 商洛学院 城乡规划与建筑工程学院，陕西 商洛 726000；2.长安大学 公路学院，陕西 西安 710064)

0 引言

全长黏结性锚杆作为边坡的一种常见支护措施，评价全长黏结性锚杆工作状态是边坡二次开挖稳定性研究的关键问题[1-3]。锚杆的特征荷载包括工作荷载及极限荷载，工作荷载指边坡处于稳定状态时锚杆所承受的荷载，极限荷载指锚杆所能承受的最大荷载[4]。

目前国内外边坡锚杆极限承载力检测方法有无损检测法及破坏性拉拔试验等。锚杆无损检测技术原理是通过锚杆端部的反射波的性质来推断锚杆工作状态[5]。Ito[6]利用X射线监测了锚固体在拉拔荷载作用下微观破坏全过程。徐景茂等[7]分析了不同岩体特性、荷载大小及试验锚固长度对锚固承载性能的影响，结果表明岩体强度越高，界面抗剪强度峰值越低。贺若兰等[8]、冯君等[9]根据拉拔实测数据，锚杆的最大轴力在端部并向深度衰减，并指出锚杆有效锚固长度与其锚固边坡的岩性有关，土层中锚杆有效锚固长度为10.0 m，而岩层锚杆的有效锚固长度仅为1.5～2.0 m。Ren 等[10]，Martin 等[11]基于三折线型黏结滑移模型，描述了锚杆界面失效特性和剪应力分布特征，最后通过现场拉拔试验验证了其准确性。姚国强等[12]通过静态拉拔荷载试验，分析了荷载作用下锚固长度对锚杆-砂浆和砂浆-岩体两锚固界面剪应力的分布影响，揭示了岩质边坡锚固机理和荷载传递机理。

关于锚杆拉拔过程中的荷载传递机理的研究已经做了大量研究。周世昌等[13]基于锚固界面的双指数曲线剪切滑移模型研究了全长锚杆的荷载传递机理。高先建等[14]、韩军等[15]、何思明等[16-17]、赵同彬等[18]、刘波等[19]研究了锚杆表面灌浆体材料块体之间的界面黏结强度及岩体强度、灌浆材料强度相对刚度等因素影响下的锚固力传递及破坏机制。尤春安等[20]研究了拉拔荷载作用下，锚固长度和锚固界面黏结强度等因素下锚固界面的变形规律及失效特性。李鹏飞等[21]基于改进的黏结滑移模型，研究锚杆弹性模量、锚杆半径、锚固长度等因素对界面剪应力分布规律的影响。黄明华等[22]、雏亿平等[23]也通过建立不同的锚杆锚固体界面力学模型，研究了锚杆渐进性破坏过程的荷载传递规律。黄生根等[24]、车纳等[25]建立锚杆拉拔试验离散元模型，研究各级荷载作用下锚杆轴力、界面剪应力分布特征以及界面失效模式。

目前锚杆荷载传递机理的研究大多采用室内拉拔试验及数值分析，通过现场原位破坏试验研究不多。本研究依托京沪高速公路加宽工程，选取既有锚杆开展原位拉拔破坏试验，研究受荷下锚杆传递机理，基于拉拔荷载-位移增量曲线，将锚杆拉拔受力全过程分为外露段变形阶段、耦合变形阶段、塑性变形阶段、脱黏阶段等4个阶段，并据此确定锚杆工作荷载，最后通过数值仿真分析，研究了极限荷载下锚杆-注浆体、锚固体-岩层两界面的剪应力分布规律，提出了锚杆极限的位移增量判定标准。

1 现场拉拔试验

1.1 工程概况

京沪高速公路(莱芜至临沂段)加宽工程沿线存在多处岩质路堑高边坡，其中K593+260～K593+555边坡多次出现变形失稳的趋势，经过补充φ32全长黏结性锚杆加固措施后边坡已经稳定。K593+260～K593+555边坡，坡高32 m，3级坡，坡率达1∶0.5，节理裂隙发育，从上往下地层分别为残积土、强风化、中风化灰岩，采取全长黏结锚杆进行支护，锚杆间距为4 m、长8 m，锚杆设计荷载为240 kN，锚固角度为20°，其工程地质剖面图如图1所示，支护参数见表1。

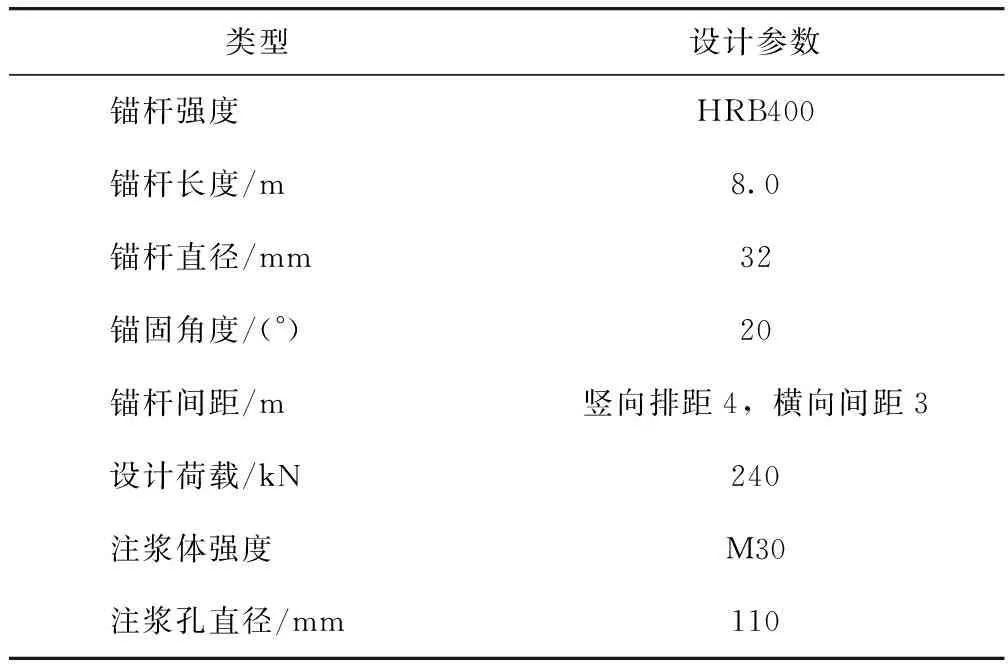
表1 既有锚杆及注浆体设计参数Tab.1 Design parameters of existing bolts and grouting bodies

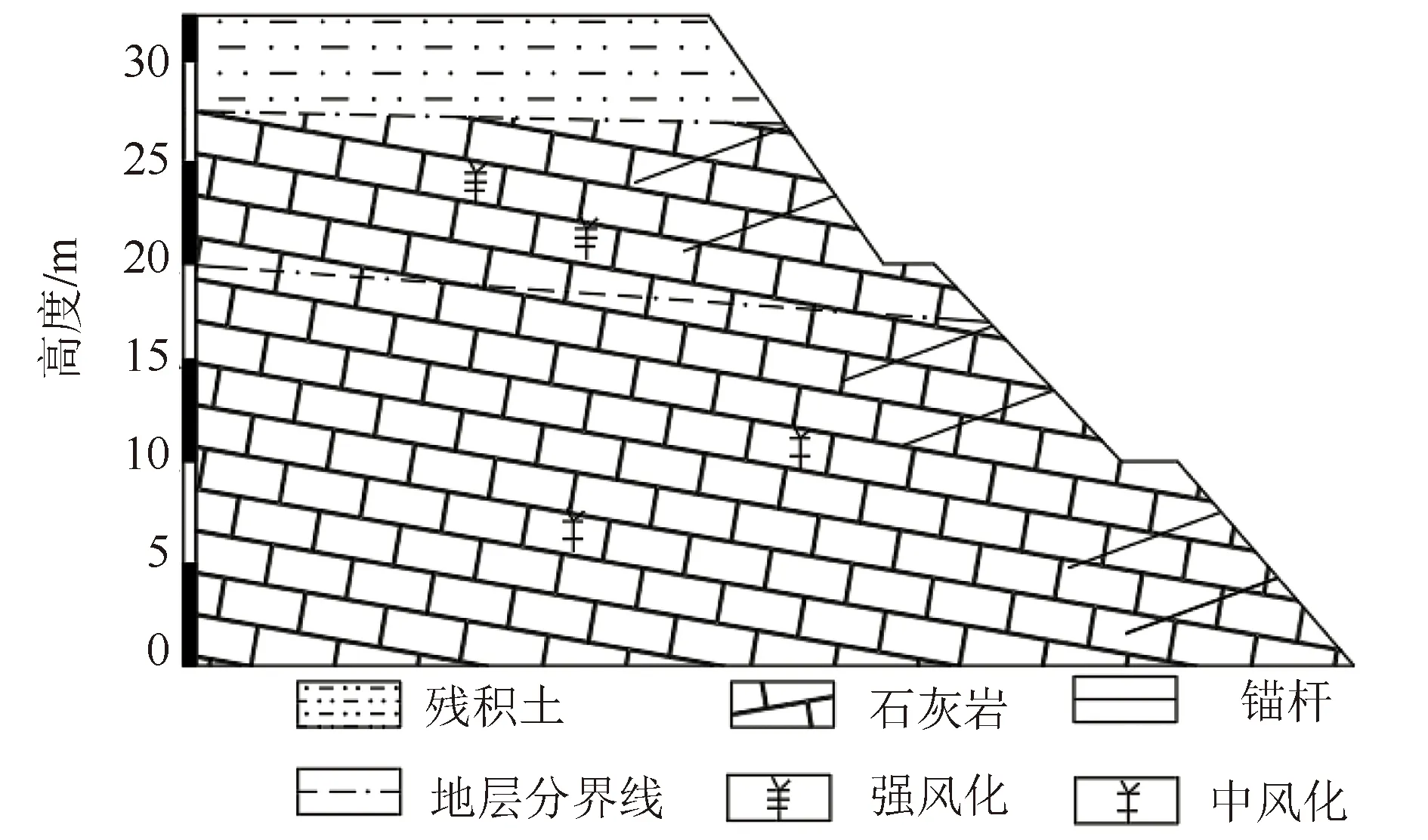
图1 K593+260～K593+555段路堑边坡Fig.1 Cutting slope of K593+260～K593+555 section

1.2 试验方案

1.2.1 试验条件及测点

为评价既有边坡的稳定性，采用原位破坏拉拔试验检测既有锚杆的工作荷载和极限荷载。试验锚杆测点选取在边坡的2，3级坡，总共选择了9根代表性锚杆进行了原位拉拔试验，测试锚杆示意图如图2所示。

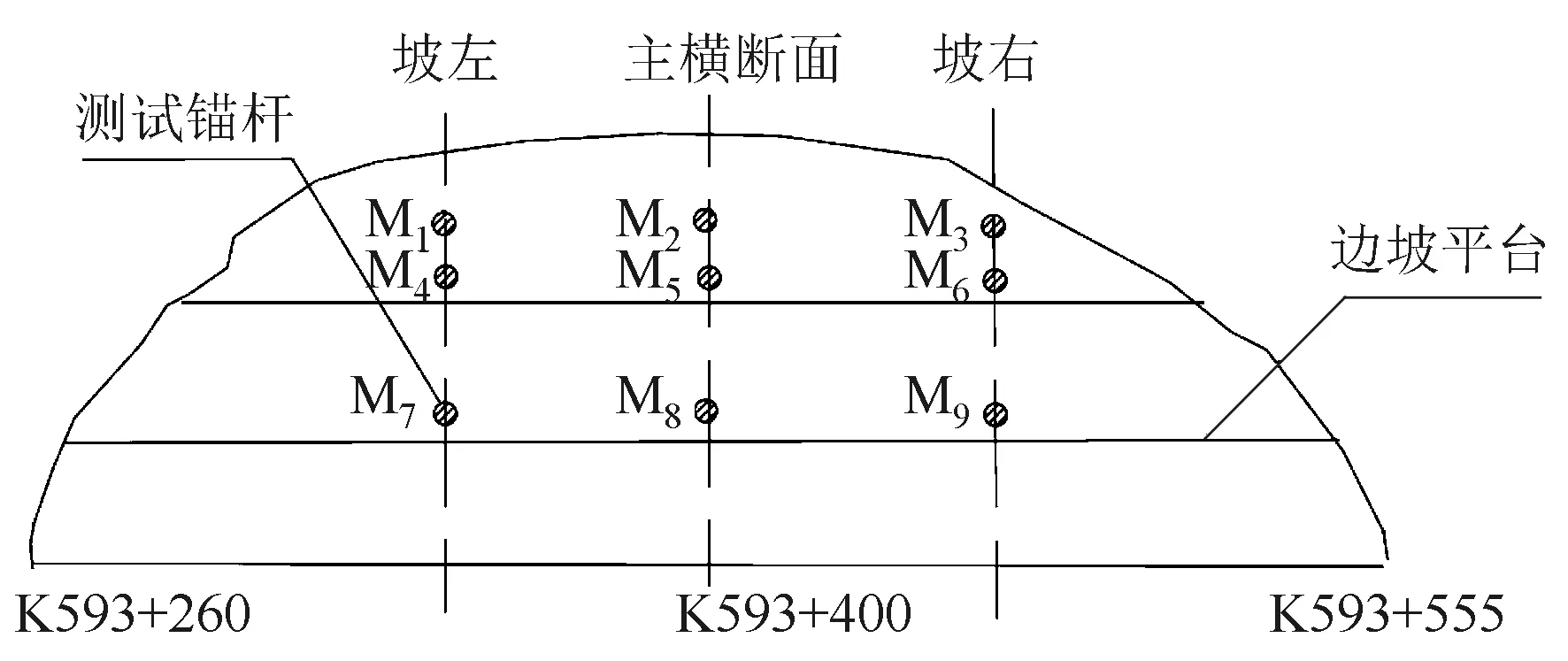
图2 测试锚杆位置示意图Fig.2 Layout of tested bolts

1.2.2 试验设备及流程

整套试验系统由加载装置、固定装置、读数装置这3部分组成。加载装置采用ZP-100T手动油压千斤顶，固定装置由锚具、楔片组成，读数装置包括位移百分表、油压表等。其工作机理为千斤顶施加向外推力至锚具，锚具将力传递给受测试的锚杆。整套试验系统如图3所示。

图3 原位拉拔试验系统Fig.3 In-situ pull-out test system

通过分级加载方式，记录加载荷载与位移百分表读数，绘制成荷载-位移曲线，通过曲线上突变点和突变区域确定锚杆的工作荷载和极限荷载，具体方法如下：

(1)锚杆外露锚头通过套筒接长，保证外露段长度至少40 cm。

(2)在锚杆的外露段先套上锚垫板，再套上液压缸，用锚杆端部的用锚具固定。

(3)检查拉拔加载设备手压泵油压表，确保加载装备初始读数为0。

(4)锚杆拉拔设备安装完毕后，为确保锚具与锚杆间紧密贴合，施加20 kN的预拉拔荷载，其后以每级10 kN的增量递增，每级荷载施加完成后，待油压表读数稳定后读取百分表位移值。

(5)当锚杆端部位移陡增，且随着拉拔荷载增加，位移持续增大，则停止加压对锚杆进行卸荷。

2 试验成果分析

2.1 锚杆拉拔试验传递机制分析

K593+260～K593+555右幅边坡3级坡及2级坡锚杆在各级荷载作用下位移增量变化曲线如图4～5所示。

图4 3级边坡锚杆荷载-位移增量曲线Fig.4 Curves of load vs. displacemental increment of level 3 slope anchor bolts

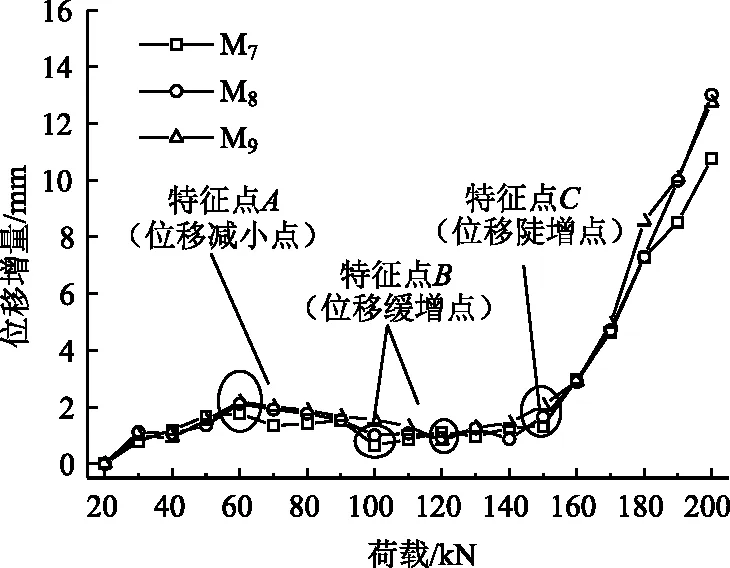
图5 2级边坡上排锚杆荷载-位移增量曲线Fig.5 Curves of load vs. displacemental increment of level 2 slope upper row anchor bolts

从图4～5可知，在拉拔荷载作用下，3级坡、2级坡锚杆荷载-位移增量曲线均呈非线性变化趋势。当拉拔荷载在20～60 kN，位移增量曲线基本呈线性增加，表明此阶段主要位移量为弹性变形；而当荷载为60～100 kN时，位移增量增速减缓，表明注浆体与锚杆的黏结力开始发挥作用；拉拔荷载在100～160 kN时，位移增量开始缓慢增加，表明注浆体产生塑性变形；当拉拔荷载超过160 kN时，荷载-位移增量曲线突然陡增，可认为锚杆-注浆体界面开始滑移脱黏，锚杆与注浆体的黏结力逐渐减小为锚杆与注浆体的侧摩阻力。

从图4～5荷载-位移增量曲线也可看出，M1～M9锚杆在各自位移突变区域内存在3个位移特征点A(位移增量减小)、特征点B(位移增量缓增)、特征点C(位移增量陡增)。M1～M9锚杆这3个特征点对应值见表2。

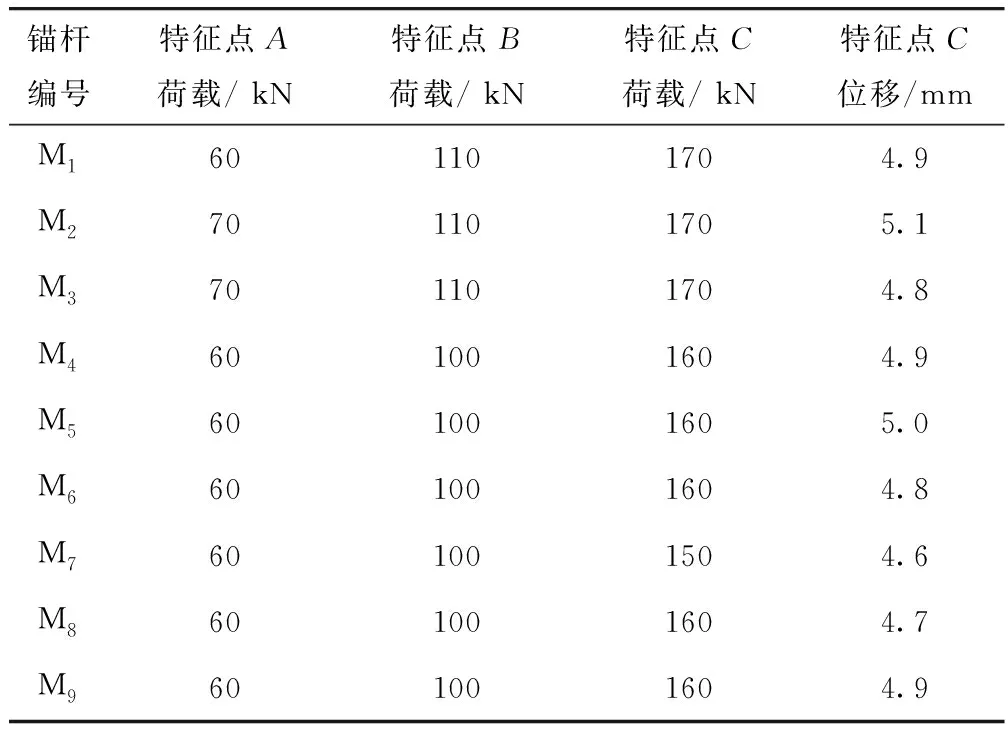
表2 现场实测锚杆特征点荷载Tab.2 In-situ measured characteristic point loads of anchor bolts

由图6可知；荷载与位移增量曲线表现为非线性，呈现出“增大-减小-缓增-陡增”的变化特征。

图6 拉拔荷载-位移增量曲线Fig.6 Curve of pull-out load vs. displacement incremental

根据曲线变化特征，进一步分析锚杆拉拔荷载作用下的荷载传递机理，可将其全过程分为4个受力阶段，如图7所示。

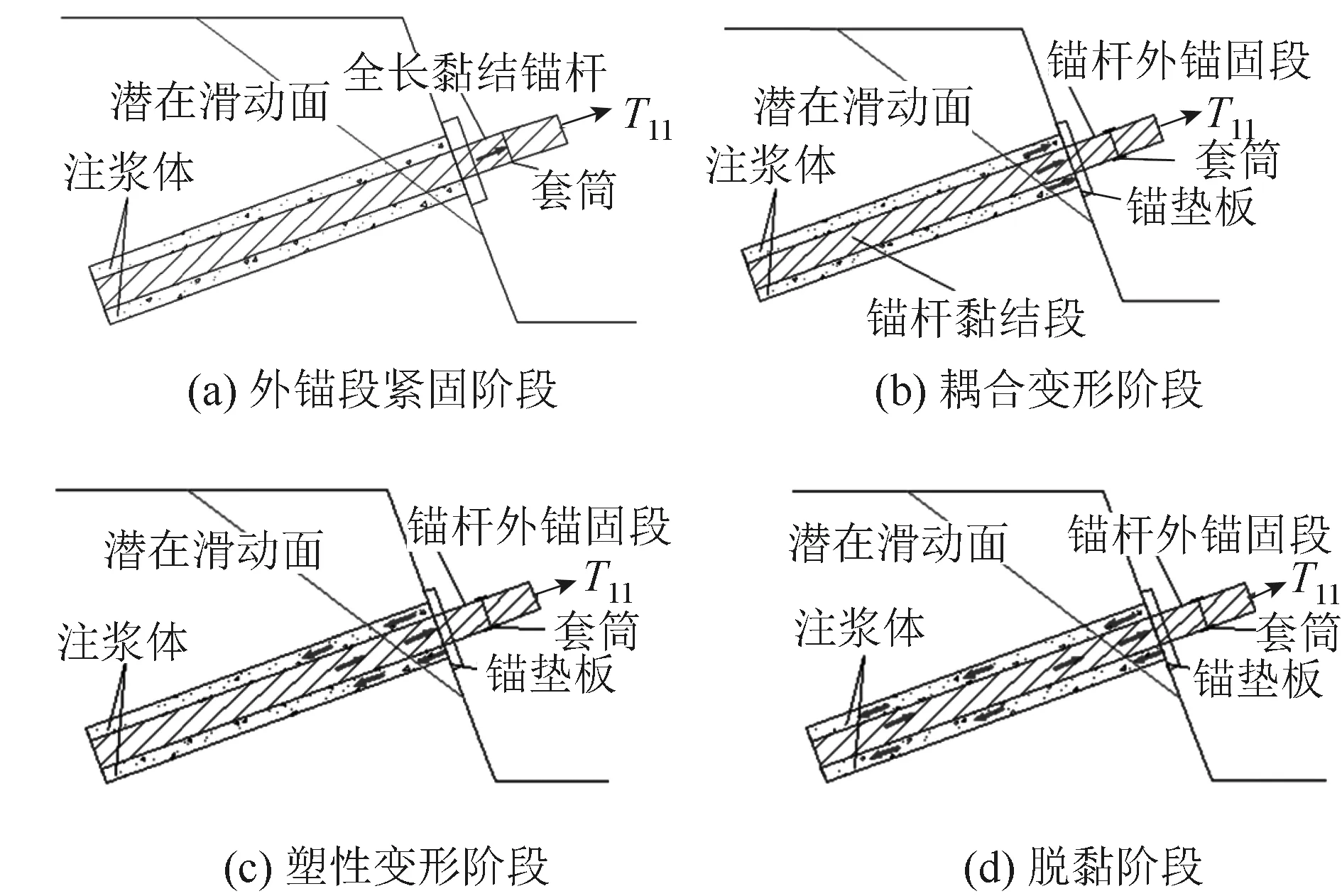
图7 拉拔试验受力阶段示意图Fig.7 Schematic diagram of stress stages during pull-out test

(1)外锚段紧固(OA)：在拉拔荷载较小时，主要为外锚段的拉拔，此阶段位移主要由锚垫板与坡面紧固、锚具与千斤顶间缝隙夹紧等引起。

(2)耦合变形阶段(AB)：随着拉拔荷载的增加，荷载传递到周围岩土体，此阶段锚杆与注浆体界面黏结力开始发挥作用，拉拔荷载需要克服锚杆与注浆体间的黏结应力，故曲线的斜率减小。

(3)塑性变形阶段(BC)：随着荷载的进一步增大，界面两侧锚杆与注浆体间的塑性变形达到一定程度，界面的黏结力逐渐减小，故曲线斜率增大。

(4)脱黏阶段(CD)：当拉拔荷载达到一定水平时，锚杆-注浆体界面只存在着残余应力，此时的残余应力仅依靠界面的摩擦力，锚杆与注浆体将完全脱黏，表现为荷载-位移(P-△S)曲线上锚端的位移增量出现明显转折点，位移出现陡增。

2.2 锚杆工作荷载确定

锚杆的工作荷载为当前状态下锚杆承受的荷载，可利用传统拐点法确定[26]。根据图7锚杆受力机理分析可知，实际中锚杆的工作荷载为一区间范围(AC段)，在锚杆-注浆体耦合变形与塑性变形阶段，此阶段在拉拔荷载作用下锚杆与注浆体协同变形，共同克服拉拔荷载产生的剪应力，可将此阶段作为锚杆工作荷载受力区间，即位移减小特征点A点与位移缓增特征点C点荷载，分别为锚杆工作荷载的最小值和最大值，工作荷载可取耦合变形与塑性变形阶段的均值。

根据锚杆拉拔受力机理结合表2中各测试锚杆的特征荷载，可得M1～M9锚杆的工作荷载见表3。

表3 各测试锚杆的工作荷载(单位：kN)Tab.3 Work load of each tested bolt(unit：kN)

由表3可知，2级坡测试锚杆(M7～M9)的工作荷载小于3级坡锚杆(M1～M3)的工作荷载，即边坡上部锚杆承担的荷载较大，表明边坡上部存在浅表层局部滑动趋势。

2.3 锚杆极限荷载确定

锚杆的极限荷载受界面黏结强度影响显著，当注浆体-岩土体界面或锚杆-注浆体界面的黏结应力无法克服拉拔产生的剪切应力，锚杆-注浆体或注浆体-岩层间无法实现同步剪切变形，会导致两界面产生滑移变形，其在荷载-位移增量曲线的表现则为位移增量的陡增，此时锚杆施加的拉拔荷载即为其极限荷载。据此方法可得到各测试锚杆的极限荷载见表4。

表4 各测试锚杆的极限荷载(单位：kN)Tab.4 Ultimate loads of each tested bolt(unit：kN)

3 锚杆拉拔数值分析

由锚杆拉拔荷载传递机制可知，位移增量陡增点对应的特征荷载即为锚杆的极限荷载，M1～M9锚杆的极限荷载对应的特征位移均为5 mm左右，可将位移增量5 mm作为极限荷载的判定标准。而不同受力荷载下的锚杆-注浆体、注浆体-岩体的界面剪应力分布形式不同，为研究极限拉拔荷载作用下两界面剪应力分布规律，开展既有锚杆拉拔数值分析试验。

3.1 模型建立

依据现场实体工程建立数值模型。模型长295 m，高60 m，锚杆横向间距为4 m，模型底部边界采用x，y，z这3个向约束，顶部自由无约束，侧边采用法向约束。锚杆拉拔试验数值模型如图8所示。

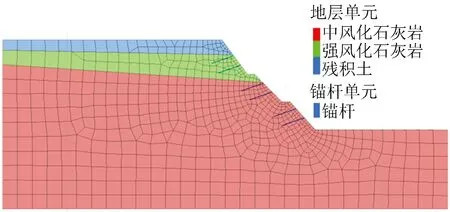
图8 拉拔试验数值模型Fig.8 Numerical model of pull-out test

全长黏结锚杆采用FLAC3D数值软件的cable单元模拟，锚杆长8 m，以1 m为结构单元段，共分成8段。岩土体采用摩尔库伦本构模型，岩土体及锚杆参数见表5～6。

表5 全长黏结锚杆计算参数Tab.5 Calculation parameters of fully bonding anchor bolt

3.2 模拟工况设置

(1)加载方案

FLAC3D中的apply命令可实现对锚杆加载，分别对M1～M9锚杆端部以单级10 kN逐级加载，并监测各级荷载下的锚杆端部节点位移。

(2)界面剪应力

采用cable模拟全长黏结锚杆时，不同锚固深度下锚杆的轴力可通过cable结构各单元段的轴力提取，锚杆-注浆体界面剪应力τ则可通过式(1)转换得到。

(1)

式中，ΔP为相邻锚杆结构单元的轴力差值；Δl为相邻锚杆结构单元的中心距；D为锚杆直径。

同样，注浆耦合体-岩体界面第2界面的剪应力则利用式(1)通过赋值方法改变锚杆cable单元几何和力学参数，将注浆体与锚杆等效为注浆耦合体，此时提取的cable单元段轴力为注浆-锚杆耦合体的轴力，此时利用式(1)可得到注浆耦合体与岩层界面的剪应力。

3.3 界面应力分布规律

选取M2测试锚杆为例，通过极限荷载前后级拉拔荷载对应的注浆耦合体-岩层、锚杆-注浆体两界面的剪应力分布规律，验证本研究所提出锚杆极限荷载判定标准，其荷载-位移增量曲线见图9。

由图9可知，数值分析中M2锚杆荷载-位移增量曲线也呈现出“增大-减小-缓增-陡增”的变化特征，与原位试验所得结果的基本保持一致，验证了数值模型的有效性。M2锚杆在数值拉拔曲线的位移陡增点170 kN处的位移增量为5.2 mm，其极限荷载前后各级荷载及对应位移增量见表7。

表7 M2锚杆荷载-位移增量Tab.7 Load and displacemental increment of bolt M2

为分析全长黏结锚杆在各级拉拔荷载下界面剪应力的分布规律，M2锚杆在150，160，170，180 kN 这4级荷载作用下，锚杆-注浆体、锚固体-岩体界面的剪应力分布规律分别如图10～11所示。

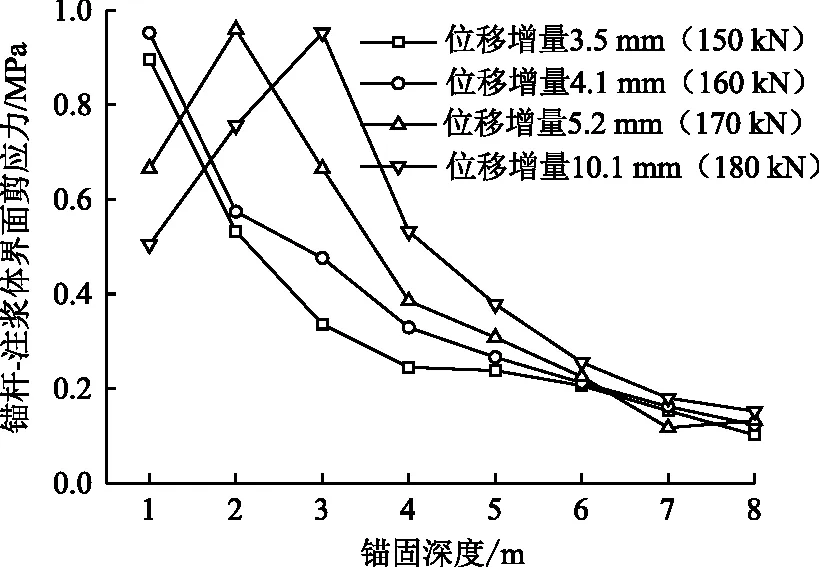
图10 M2锚杆-注浆体界面剪应力分布Fig.10 Shear stress distribution of interface between bolt M2 and grouting

图11 锚固体-岩体界面剪应力分布Fig.11 Shear stress distribution of interface between anchorage and rock mass

由图10～11可知，不同拉拔荷载下，锚杆-注浆体界面、锚固体-岩层界面的剪应力呈非均匀分布，且存在“单调递减”与“单峰分布”两种分布形式。拉拔荷载在150～160 kN时，剪应力在锚端达到最大值，并随锚固深度增大逐渐向底部衰减，即沿锚固深度呈“单调递减分布”。当荷载增至170 kN时，界面剪应力转变为“单峰分布”，最大剪应力峰值埋深增大，主要是因为当拉拔荷载增至界面剪应力极限黏结强度时，其接触界面发生脱黏，拉拔荷载的主要承载区段转移至深部，剪应力峰值即为该锚固段界面的极限黏结强度。拉拔荷载为180 kN时，接触界面剪应力分布形式仍表现为单峰分布模式，但出现峰值内移现象，主要是由于初始加载时尚未达到锚固系统的最大支护能力，而随拉拔荷载增大又超出其最大支护能力。由于接触界面发生黏结滑移，造成拉拔荷载重分布，拉拔荷载传至锚固段深处，故内外层剪应力变化规律协调一致。

综上所述：荷载拉拔达到170 kN时，两界面的剪应力分布形式均由“单调递减”转为“单峰分布”，继续增大拉拔荷载，剪应力峰值保持不变，但峰值位置下移，表明170 kN为M2锚杆极限荷载，而此时的位移增量为锚杆的特征位移，可认为M2剪应力峰值对应的位移增量点为判断极限荷载特征点，即位移增量达到5.2 mm时锚杆的极限荷载为170 kN。采取同样的试验方法，M2～M9各测试锚杆极限荷载-位移增量见表8。

表8 各锚杆极限荷载对应的位移增量 (单位：mm)Tab.8 Displacemental increment of bolts under ultimate load (unit：mm)

由表8可知M1～M9锚杆拉拔荷载达到极限荷载时，所对应的位移增量为4.8～5.2 mm，与现场原位拉拔试验5 mm左右位移增量基本保持一致，表明了以位移增量为依据，判定锚杆极限荷载的方法具有适用性，因此将锚杆单级位移增量5 mm所对应荷载视为确定锚杆极限荷载的快速判定方式。

4 结论

本研究通过 9组既有锚杆进行拉拔破坏现场试验和拉拔试验数值分析，根据荷载-位移增量曲线和界面剪应力分布特征得出如下结论：

(1)对9根锚杆进行现场拉拔试验，荷载-位移增量曲线趋势大致相同，均经历外锚段紧固阶段、耦合变形阶段、塑性变形阶段、脱黏4个受力阶段，其中耦合变形-塑性变形阶段、脱黏阶段分别对应的荷载是锚杆工作荷载、极限荷载。

(2)锚杆处于工作荷载阶段，锚杆-注浆体界面、锚固体-岩层界面的剪应力分布形式均呈“单调递减模式”；当锚杆达到极限荷载时，界面的剪应力分布形式由“单调递减”转变为“单峰分布”，且随着拉拔荷载的增加，界面剪应力峰值向深部移动。

(3)锚杆位移增量为5 mm左右时，现场实测位移增量-荷载曲线出现陡增，且拉拔数值试验中两界面剪应力峰值不再增加，界面黏结强度达到极限黏结强度，锚杆的位移增量也为5 mm左右，可用位移增量判定锚杆极限荷载。