基于CPT试验的多年冻土区路表变形风险评价
田 波,王昊武,权 磊,谢晋德,朱旭伟
(交通运输部公路科学研究院,北京 100088)
0 引言
多年冻土之上夏季融化冬季冻结的土层为活动层,是冻土路基沉降变形的主要影响因素。全球气候变暖导致青藏高原多年冻土不断退化,温差、荷载及地质病害耦合作用下路面变形持续发展,严重影响交通安全。
冻土地区路面发生变形的主要原因是冻土热融变形,即冻融循环后,土体体积和孔隙率增加进而导致内聚力和单轴抗压强度降低,从而导致冻胀变形及融化变形[1-3]。已有针对冻土地区土体力学特性演化的本构模型主要来源于室内试验[4-5],且多于简单应力状态下考察冻土的强度和蠕变特性,因此适用范围较小,而现场服役条件较为复杂,目前研究成果未能精确满足冻土地区工程的使用需求。
多年冻土区路面沉降主要有3个变形源[6]:冻土解冻导致沉降、修建路面导致冻土升温而产生活动层未冻土体蠕变、活动层冻融循环改变土体性质而产生额外沉降。目前国内外类似工况的处治方案在处理3个变形源交互作用方面存在明显局限[7-8]。陈冬根等[9]指出冻融循环后饱冰冻土层变形风险大于浅地表层和路基填土。王锐等[10]发现含冰量、路堤填土高度的增加会增加路面变形风险。可见目前针对冻土区路面沉降风险评价的研究较少,缺乏适用于冻土区路面沉降风险的评估方法和处理技术。
在众多原位测试方法中,静力触探试验(CPT)能够间接评价较大深度范围地层的力学参数,适合深厚冻土层承载能力评价[11-12]。目前CPT技术已应用于软土地区的土体承载力、土层划分及沉降风险评价等方面[13-15],但鲜有应用于多年冻土区的研究成果。本研究拟利用CPT分析青藏多年冻土活动层承载特性,并提出相应路表变形风险评估方法。
1 测点选择与试验方案
1.1 测区概况
青藏地区受高海拔影响,分布大片多年冻土,属中低纬度多年冻土,与高纬度多年冻土差异较大,更易受到青藏高原湿热化倾向的影响[16-17]。本研究测试路段位于青藏高原东缘,海拔大部分在4 500~5 000 m之间,年平均气温约为-3.3 ℃,雨季集中在夏季,年降水量约为387 mm。正因如此,当地存在明显暖季活动层,这也成为青藏地区公路路基热融变形的外界条件[18]。
选取青藏地区既有公路路表不均匀融沉变形较大的路段约15 km,现场勘测发现该地区旧、新路共同服役,前者最早修建于1954年,虽通车后不断采取加铺、修补等管养措施,但仍持续融沉;后者于2017年通车运营,虽辅以热棒、片块石、通风管等路基结构保护冻土,但仍存在部分路段产生不同程度的路表变形。
1.2 CPT触探方案
为深入探究路表变形程度不同路段的下伏冻土层承载特性,并验证CPT技术在冻土地区的适用性,因此采取单桥、双桥静力触探的方法开展试验,分别布置12个测点,试验时间为7月,前者试验路段路基结构类型为片块石路基和普通路基,后者试验路段路基结构类型为通风管路基和热棒路基,由于路表沉降是个持续性的行为,因此所选测点避开经加铺处理的区域。各测点路表沉降最大值如图1所示(PKS为片块石路基,PT为普通路基,TFG为通风管路基,RB为热棒路基)。
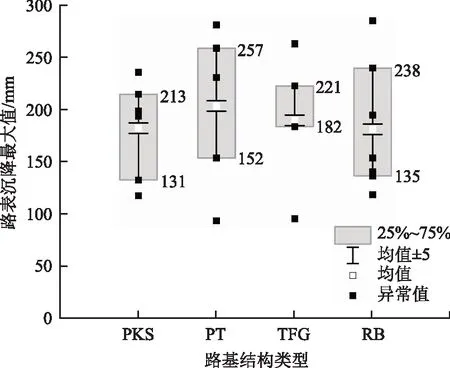
图1 各测点路表沉降最大值Fig.1 Maximum settlement of road surface at each measuring point
从图1中可看出,4种路基结构类型对应路段路表沉降量差异不大,未呈明显分区,即路表沉降行为受路基结构类型影响较小,因此均存在不同程度的路表沉降。
根据软土地基的使用经验,CPT在碎石土中有一定缺陷性,鉴于此本研究在试验阶段选择场地时,依据既有地质勘测资料,选择冻土黏土地层。如何保障CPT在冻结碎石土层中的应用,今后是一个值得探讨的研究方向。根据地质勘测资料可知,路线两侧10 m范围内场地基本均匀。限于静力触探设备在公路上方进行直接作业难度大,本研究中触探孔设置于公路两侧原地面,测点至坡脚距离不超过10 m,具体布设点位如图2所示。
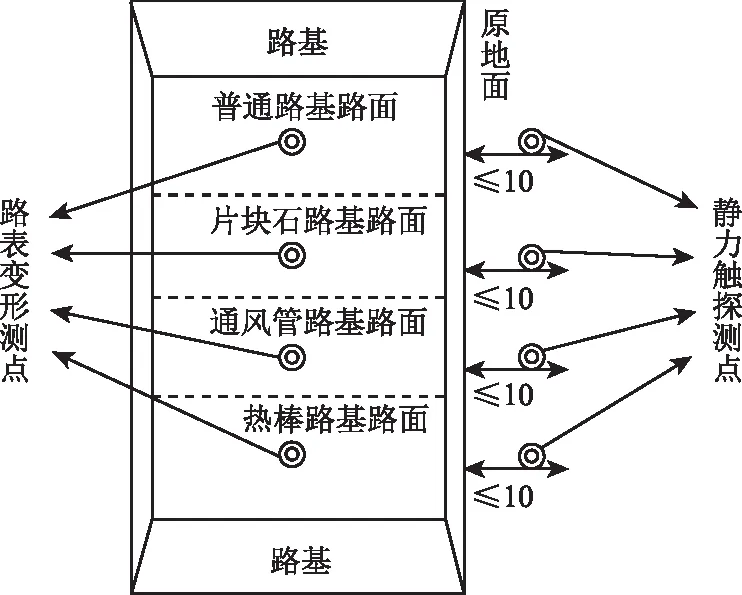
图2 测点布设(单位:m)Fig.2 Test points layout(unit:m)
2 一般规律分析
2.1 比贯入阻力
通过现场单桥静力触探试验测得片块石路基、普通路基路段活动层比贯入阻力,分别以3个测点为例进行分析,Ps-d曲线如图3所示。
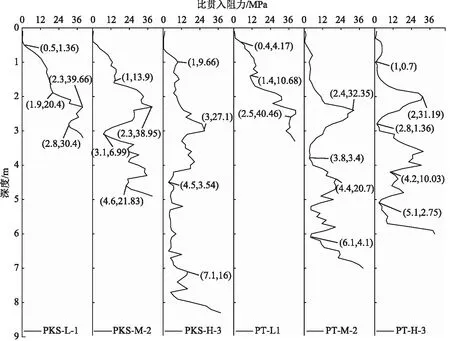
图3 活动层Ps-d曲线Fig.3 Ps-d curves of foundation
从图3中可以看出:
(1)多年冻土区活动层比贯入阻力随深度不断波动,总体来看呈增加趋势,但是存在部分陡降的情况,达到一定深度后不断增加直至无法贯入;同时,活动层比贯入阻力随深度分布具有分层的特点,包含软弱层和持力层。
(2)活动层比贯入阻力与路表变形行为具备一定关联性。路表沉降严重的测点,活动层比贯入阻力总体偏小且软弱层厚度较大。如PT-H-3测点路表沉降较大,其比贯入阻力峰值约为27.1 MPa,贯入中止深度为6 m,而PT-L-1测点路表变形较小,其比贯入阻力峰值达40.46 MPa,贯入中止深度仅为3.3 m。
(3)活动层贯入中止深度由比贯入阻力峰值决定,当贯入试验达到极限深度时,比贯入阻力约为37 MPa。活动层比贯入阻力谷值及其深度区间共同决定其承载能力的下限。也就是说,路表变形严重程度受活动层比贯入阻力较小值及其厚度共同影响。
2.2 锥尖阻力
通过现场双桥静力触探试验测得通风管路基、热棒路基路段活动层锥尖阻力,分别以3个测点为例进行分析,qc-d曲线如图4所示。
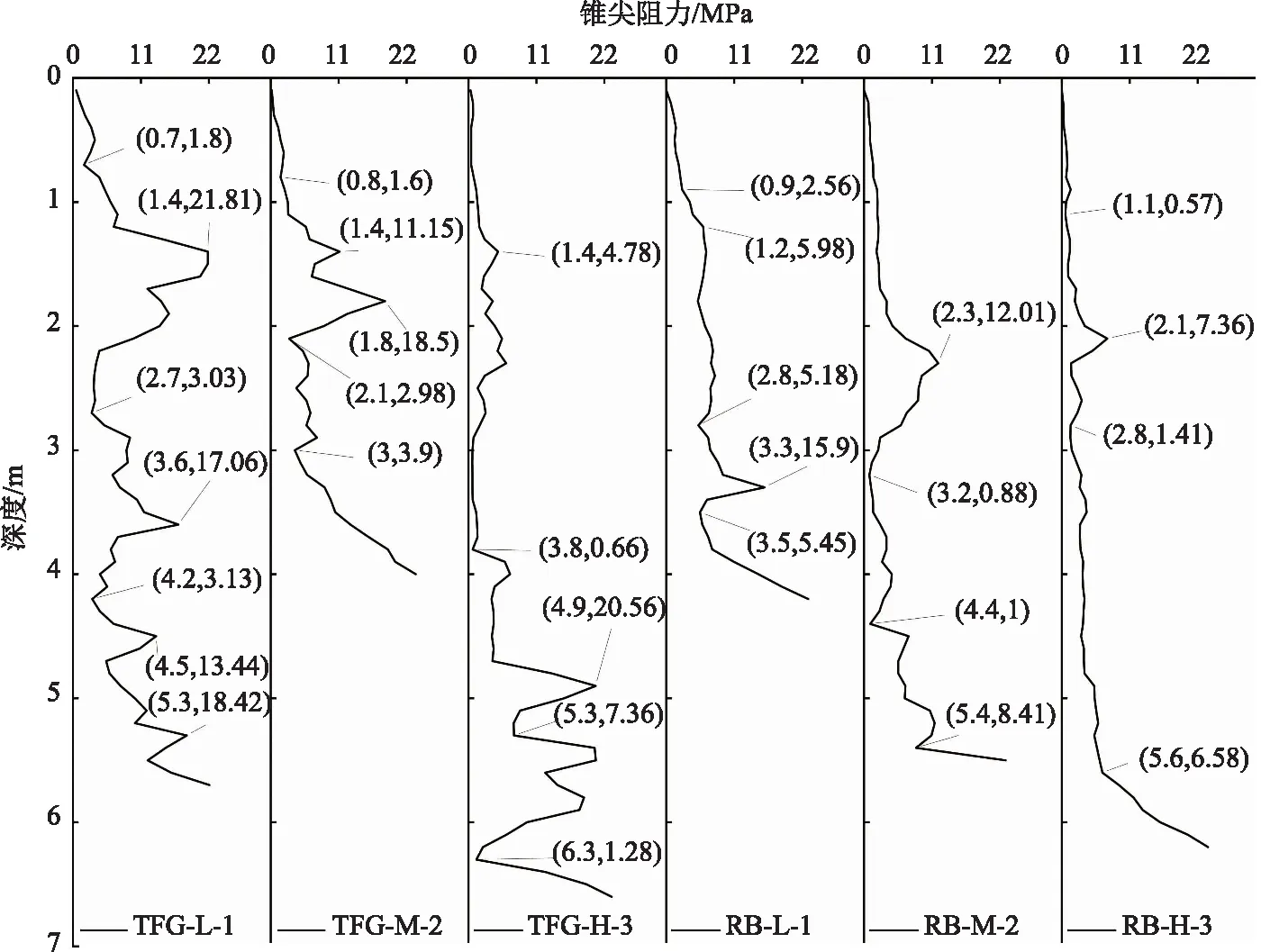
图4 活动层qc-d曲线Fig.4 qc-d curves of foundation
从图4中可以看出:
(1)多年冻土区活动层锥尖阻力随深度波动式增加,也存在间断性陡降的情况,达到一定深度后不断增加直至无法贯入。与比贯入阻力相比,锥尖阻力随深度分布的分层特点更为明显。
(2)活动层锥尖阻力与路表变形行为具备一定关联性。路表沉降严重的测点,活动层锥尖阻力总体偏小且软弱层厚度较大。如RB-H-3测点路表变形较大,其锥尖阻力峰值约为7.36 MPa,贯入中止深度为6.2 m,而TFG-L-1测点路表变形较小,其锥尖阻力峰值达21.81 MPa,贯入中止深度为5.7 m。
(3)活动层贯入中止深度由锥尖阻力峰值决定,当贯入试验达到极限深度时,锥尖阻力约为22 MPa。活动层锥尖阻力谷值及其深度区间共同决定其承载能力的下限。与比贯入阻力相同,路表变形严重程度受活动层锥尖阻力较小值及其厚度共同影响。
2.3 侧壁摩阻力
通过现场双桥静力触探试验测得通风管路基、热棒路基路段活动层侧壁摩阻力,分别以3个测点为例进行分析,fs-d曲线如图5所示。
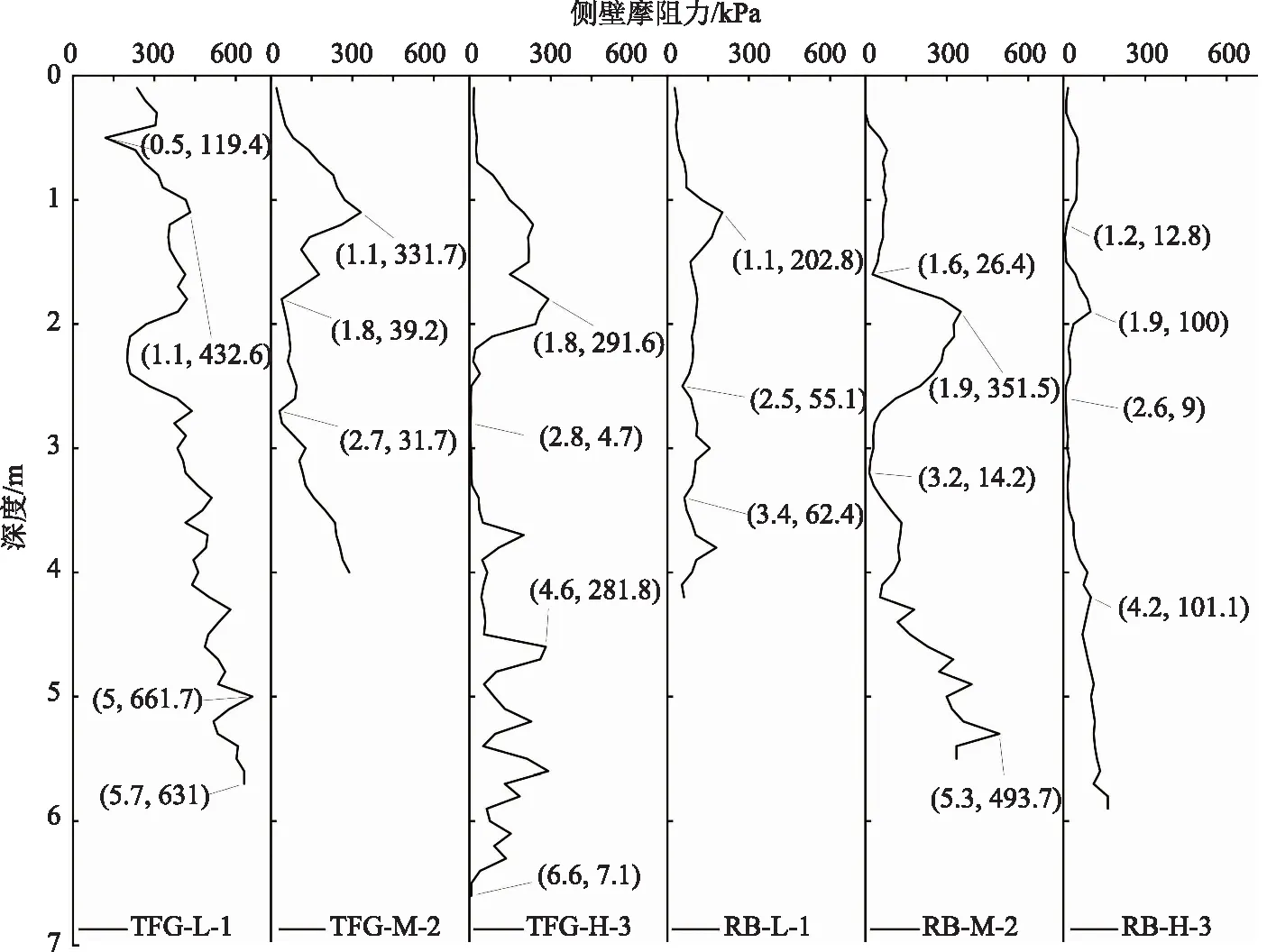
图5 活动层fs-d曲线Fig.5 fs-d curves of foundation
从图5中可以看出:
(1)多年冻土区活动层侧壁摩阻力随深度不断波动,伴随间断性陡降现象。贯入中止时的侧壁摩阻力无明显规律,也就是说,侧壁摩阻力大小与贯入中止行为呈弱相关。
(2)活动层侧壁摩阻力与路表沉降情况关联性不强。路表沉降严重的测点,活动层侧壁摩阻力未见明显趋势。如TFG-L-1测点路表变形较小,侧壁摩阻力峰值约为661.7 kPa,而贯入中止深度达5.7 m;TFG-M-2测点路表变形较大,侧壁摩阻力峰值约为331.7 kPa,而贯入中止深度仅为3.9 m。
3 基于CPT试验的路表沉降风险评价
3.1 包络面积比
由前文分析结论可知,多年冻土区路表沉降情况受路基结构类型影响较小,与活动层比贯入阻力、锥尖阻力相关性较高,而两者对应的深度曲线波动复杂,通过深度和峰值、谷值难以准确评价活动层承载能力。因此,需提出一个综合评价指标对活动层比贯入阻力和锥尖阻力进行量化。由于活动层承载能力与比贯入阻力、锥尖阻力的谷值及深度区间密切相关,考虑结合各指标值大小和深度范围计算得到包络面积,而深度对包络面积影响较大,为此通过给定一个参数标准值,计算各指标在该标准要求下的包络面积所占百分比,以消除深度的影响,计算如式(1)所示:
(1)
式中,R为包络面积比;A为Ps-d曲线或qc-d曲线与y轴形成的面积;d为深度;k为参数标准值。
为确定活动层比贯入阻力和锥尖阻力合理的参数标准值k,基于深度曲线的峰值、谷值各拟定6组标准值,分别计算包络面积比,并与路表变形最大值进行回归分析,以PKS-L-1测点为例,包络面积比计算示意图如图6所示,回归分析结果如图7所示。
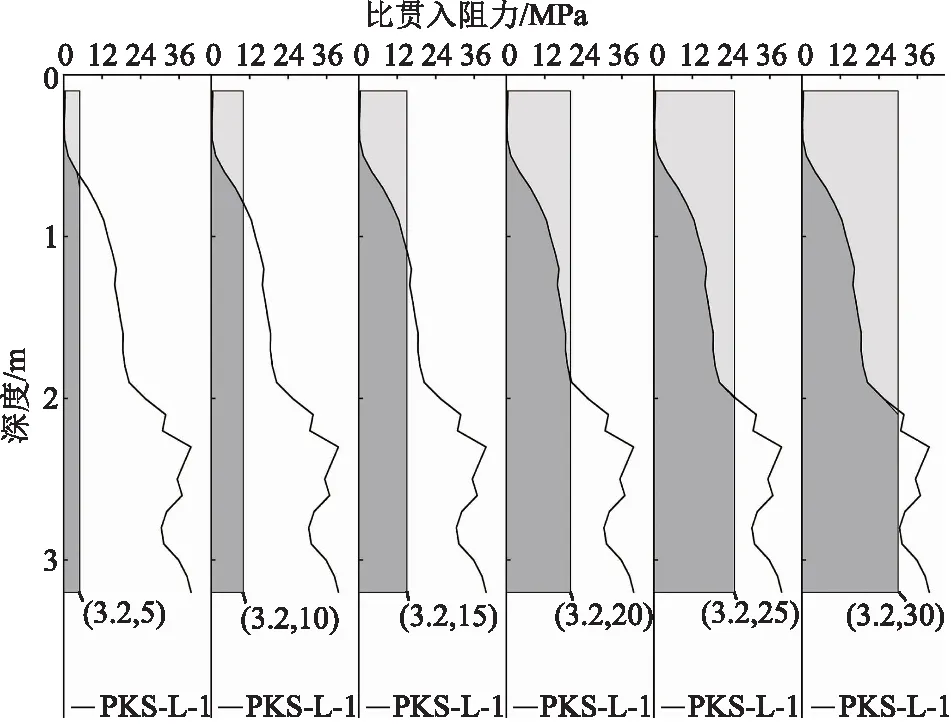
图6 包络面积比计算示意图Fig.6 Schematic diagram of calculation of envelope area ratio
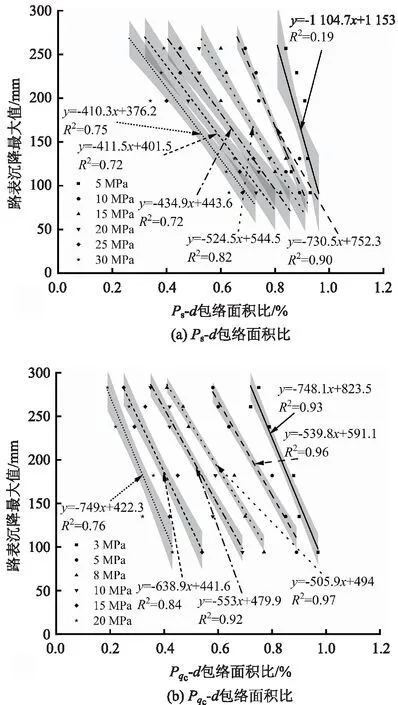
图7 路表沉降行为与包络面积比关联表征Fig.7 Correlation between surface settlement behavior and envelope area ratio
由图7可看出,活动层Ps-d曲线和qc-d曲线的包络面积比越大,相应路表沉降最大值均呈下降趋势,即包络面积比可反映活动层承载能力,包络面积比越大,活动层承载能力越强,路表沉降越小。线性回归结果表明,活动层比贯入阻力标准值为10 MPa、锥尖阻力标准值为8 MPa时,路表沉降最大值与包络面积比相关性最高,因此建议试验所在地区比贯入阻力和锥尖阻力标准值分别取10 MPa和8 MPa。
3.2 风险评价模型
由前文可知,活动层Ps-d曲线和qc-d曲线的包络面积比可表征其承载能力,且与路表沉降最大值线性相关,故可提出包络面积比与路表沉降最大值的经验公式。由于路表沉降行为随时间动态发展,而该经验公式未涉及时间因素,因此考虑以该公式计算路表沉降最大值,表征活动层对应区域路表发生沉降的风险。由图7可看出,活动层比贯入阻力和锥尖阻力标准值分别取10 MPa和8 MPa时,12处测点深度曲线的包络面积比与路表沉降最大值线性回归的决定系数均达0.9以上,具有十分良好的拟合效果。由此,建立路表沉降风险评价模型如式(2)~(3)所示:
y=-730.5Rp+752.3,
(2)
y=-505.9Rq+494,
(3)
式中,y为路表沉降最大值;Rp为活动层Ps-d曲线包络面积比;Rq为活动层qc-d曲线包络面积比。
提出路表沉降风险分级方法对冻土地区公路施工具有一定参考价值,因此参考规范《公路技术状况评定标准》(JTG 5210—2018)[19]中路基沉降和路面沉陷的分类方法,将冻土区路表沉降风险分为轻、中、重3个等级,分别对应路表沉降最大值为0~50,50~150,>150 mm,计算包络面积比可得分类标准见表1。

表1 路表沉降风险等级Tab.1 Road surface subsidence risk levels
3.3 模型精度评估
为评估路表沉降风险评价模型实际应用的精度,由同期静力触探试验中的另外12处测点数据计算包络面积比,代入式(1)~(2)计算路表沉降最大值,求得与实测路表沉降最大值间的绝对误差见表2。
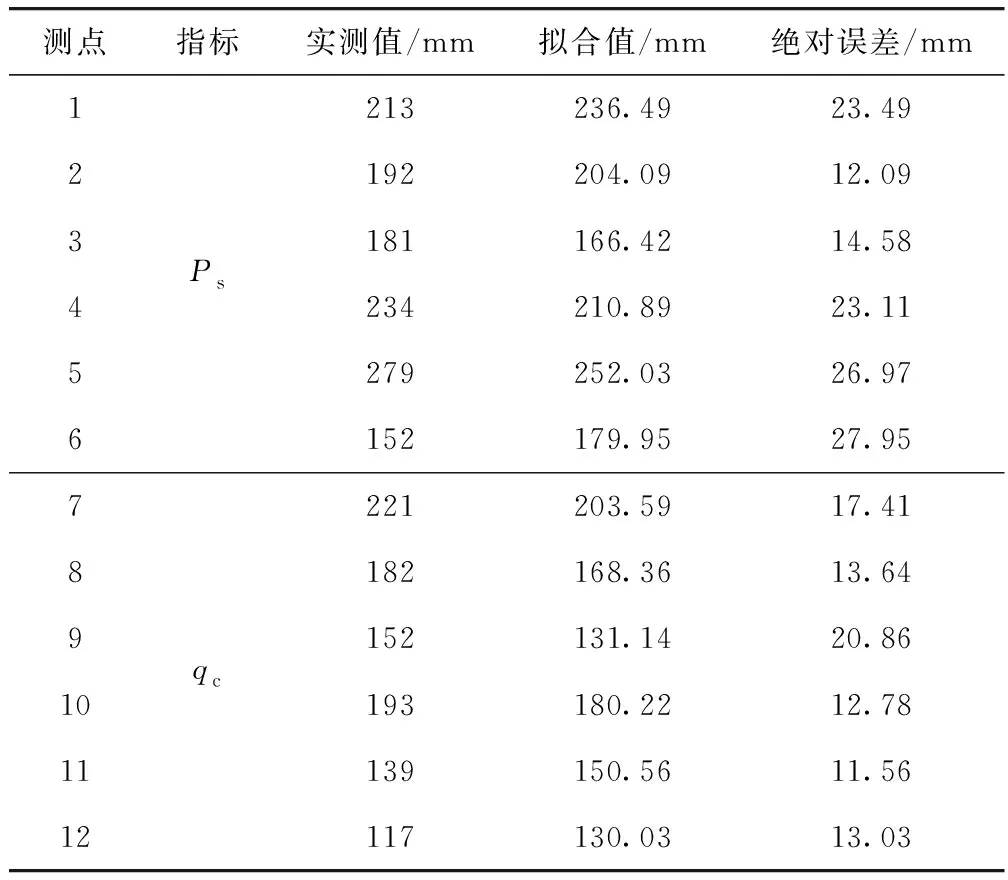
表2 路表最大沉降拟合误差值Tab.2 Fitting error values of maximum settlement of road surface
由表2可知,活动层比贯入阻力和锥尖阻力估算的路表沉降最大值与实测值绝对误差较小,前者6个测点绝对误差均值为21.36 mm,后者6个测点绝对误差均值为14.88 mm,显然,该模型精度较高,因此可用于评价多年冻土区路表沉降风险。
4 结论
本研究通过静力触探试验研究多年冻土区浅部地层的承载特性,结合路表沉降数据进行关联分析,主要得到以下结论:
(1)路表沉降行为受路基结构类型影响较小,与活动层比贯入阻力或锥尖阻力关联性较强,比贯入阻力、锥尖阻力越大,可贯入深度越小,承载能力越强,路表变形越小。
(2)当贯入试验达到极限深度时,地层比贯入阻力约为37 MPa、锥尖阻力约为22 MPa,且两者较小值及其厚度范围共同决定地层承载能力的下限,影响路表变形范围。
(3)提出了包络面积比以定量评价活动层承载能力,建议试验所在地区的比贯入阻力和锥尖阻力标准值分别取10 MPa和8 MPa,且包络面积比越大,活动层承载能力越强,路表沉降越小。
(4)通过线性回归分析,建立包络面积比与路表沉降最大值的相关经验公式,其决定系数均在0.9以上,该公式对路表沉降最大值随包络面积比变化规律的表达较为直观,并提出了较适宜于多年冻土区路表沉降风险评价的等级及标准。

