逆变器谐波注入引发电池包单体电芯电压跳变问题研究

陈石人 黄勇 肖曦 杨凡 舒朝雷

（威马汽车科技集团有限公司，成都 610000）

1 前言

在纯电动汽车动力总成控制软件中，谐波注入被广泛应用。廖勇等[1]应用谐波注入改善电流波形，抑制电磁转矩脉动；于吉坤等[2-3]利用离散傅里叶变换进行永磁同步电机谐波分析，提出了一种谐波注入脉冲宽度调制（Pulse Width Modulation，PWM）方法，有效抑制了纹波电流；于慎波等[4]用谐波注入法改善永磁同步电机的运动特性，降低电机振动，并分析了转矩脉动抑制效果；Najmabadi等[5]重点分析了注入电流灵敏度对电机转矩脉动消除的影响。

以上文献主要研究了谐波注入对电机总成自身的影响，未涉及其对纯电动汽车电网络的影响。卿宴伶等[6]研究表明，在交-直-交电力机车系统中，为提高系统功率因数而提高高次谐波含量，容易引起高次谐波谐振。因此，在纯电动汽车整车电网络中，谐波注入很可能引发系统中如电池包、高低压直流变换器（DC/DC）、车载 充 电 器（On Board Charger，OBC）等部件的问题，如电池包单体电芯电压跳变[7-10]。

本文针对某纯电动车型下线路试中单体电芯电压跳变过大引发制动失速和加速抖动等问题，分析问题产生的原因，并建立整车电网络模型，计算整车电网络系统谐振点，并对谐波注入策略进行优化，最后开展实车试验验证优化策略的有效性。

2 逆变器谐波注入问题分析

某纯电动车型在下线路试中，由于单体电芯电压跳变过大（>250 mV）引发系列问题：在高荷电状态（State of Charge，SOC）情况下出现制动失速，原因是单体电芯电压瞬间跳变到4 300 mV 以上，能量回收功能被禁止；在低SOC 情况下满油门加速时抖动，原因是单体电压瞬间跳变到3 200 mV 以下，触发能量管理欠压保护，电机输出功率受限。

对问题进行定位，排除电池管理系统（Battery Management System，BMS）软硬件、单体电芯质量问题和整车电磁干扰后，发现搭载动力总成A 时单体电芯电压无跳变，搭载动力总成B 且仅逆变器软件版本低于V1.10 时存在单体电芯电压跳变问题。因此，问题原因定位为动力总成B的逆变器软件。

整车单体电芯电压跳变情况如图1所示，2款动力总成相关参数如表1所示。

表1 动力总成参数

图1 单体电压跳变

动力总成B 的逆变器软件V1.10 版本与更早的版本相比，最大差异是谐波注入参数不同。

2.1 整车电网络模型建立

逆变器软件的谐波注入参数不同，导致单体电芯电压跳变最可能的原因是谐波注入的频率与整车电网络系统谐振点重合，谐波电流幅值被放大，谐波含量提高。

纯电动汽车电网络可简化为由母线电容C、整车线束寄生电感L、动力电池内阻及寄生电感等组成，整车电网络确定后谐振点即确定，谐振点不会随电气参数的变化而改变。

为求解整车谐振网络的谐振点，首先需建立直流侧模型。完整模型涉及用电设备较多，模型非常复杂，现阶段主要关注电池和逆变器间的谐振问题，为此得到直流侧的简化模型如图2 所示。将电池等效为由电阻、电感、理想电压源串联构成，线束等效为由电阻、电感串联构成，电容等效为由电阻、电感、理想电容串联构成，逆变器等效为理想电流源。

图2 交直流简化模型

由主电路拓扑工作原理可知，电路中含有直流量和交流量，而母线电容和系统寄生参数主要对交流量起作用，进一步化简模型，如图3 所示。电池/母线模型可简化为由等效电阻和电感串联构成。

图3 交流简化模型

2.2 整车电网络参数计算

由图2 和图3 可知，电池包母线电流ibus和母线电压vbus可以通过测量电池包母线进行频谱分析得出，由于系统中逆变器模型电流idc作为谐波源不易测试，只能通过母线电流和电压波动来估算模型参数。电容已知，电容直流侧寄生等效电阻、等效电感对模型影响很小，本文通过估算求得交流简化模型中寄生电阻Rbb和寄生电感Lbb：

式中，vbus(f1)、vbus(f2)分别为频率f1、f2下的电压；ibus(f1)、ibus(f2)分别为频率f1、f2下的电流。

使用泰克TBS2000B 示波器测试车辆正常行驶数据，选取其中一段数据进行快速傅里叶变换（Fast Fourier Transform，FFT）频谱分析，如图4 所示。将此时1 400 Hz 和2 790 Hz 频率下的vbus和ibus代入式（1）和式（2），计算获得寄生电阻Rbb=46.5 mΩ、寄生电感Lbb=9.1 μH。

图4 母线电压和电流幅频特性

2.3 谐振点及电流增益计算

根据电池系统与逆变器系统间的交流简化模型（见图3）和基尔霍夫电流定律可得复频域形式传递函数：

式中，Hbusi-i(s)为电流转移复频域传递函数；Hbusv-i(s)为电压转移复频域传递函数。

由于ibus为电池包-母线模型测量电流，已经滤波，而idc为逆变器模型电流，为谐振源，二者比值作伯德（Bode）图，可以得到系统谐振点和电流增益。

电容模型和逆变器模型中，电阻、电容和电感均为已知固定值，根据图3可得：

式中，RC为整车电网络电容模型电阻，约为0.2 mΩ；C为逆变器电容，约为370 μF（整个电网络系统电容约407 μF）；LC为电容模型电感，约为20 nH；iC为电容模型电流；Lbus2为测量点后直流母线导线电感：

式中，μ0为母线真空导磁率，取1.25 664 μH/m；r为直流母线半径，取0.004 m；l为测量点后的直流母线长度，取0.5 m。

经计算，Lbus2约为0.477 nH。

将式（5）~式（9）代入式（3）、式（4），可以分别得到：

将已知参数同时带入相应的传递函数，根据计算结果作Bode图，如图5所示。

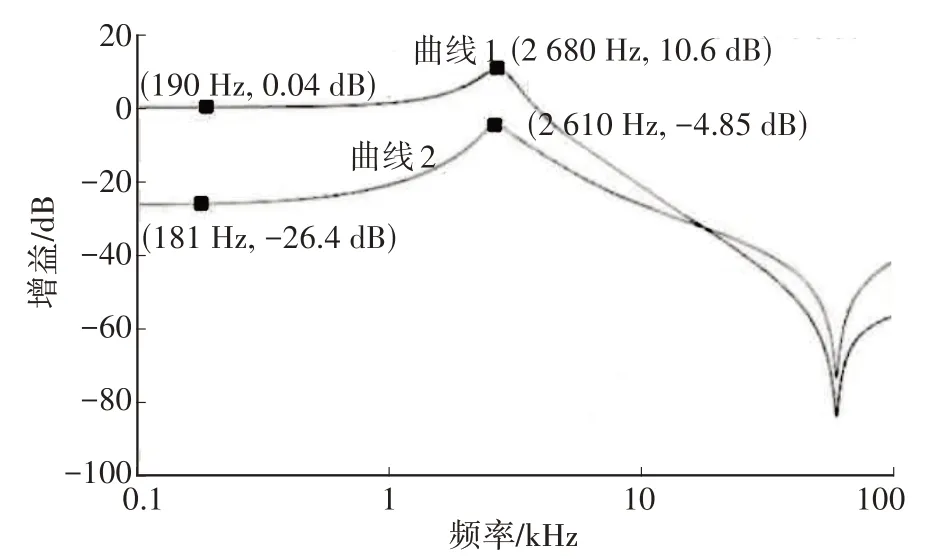
图5 Bode图

从图5 中可以看出，电流的增益约为10.6 dB，系统谐振点约为2.6 kHz，谐振区间为2~3 kHz，通过电流转移传递函数或者电压转移传递函数可以得到几乎相同的谐振区。

3 谐波注入参数优化

谐波是频率为基波频率整数倍的一种正弦波。由于存在非线性元件和非线性负载，电网的电压或电流的波形包括频率为50 Hz的正弦波（基波）和与基波频率（50 Hz）成整数倍和分数倍频率的其他正弦波。

3.1 优化前逆变器软件谐波注入参数

单体电芯电压跳变所对应的V1.09 版动力总成B逆变器控制器软件谐波注入参数如表2所示。

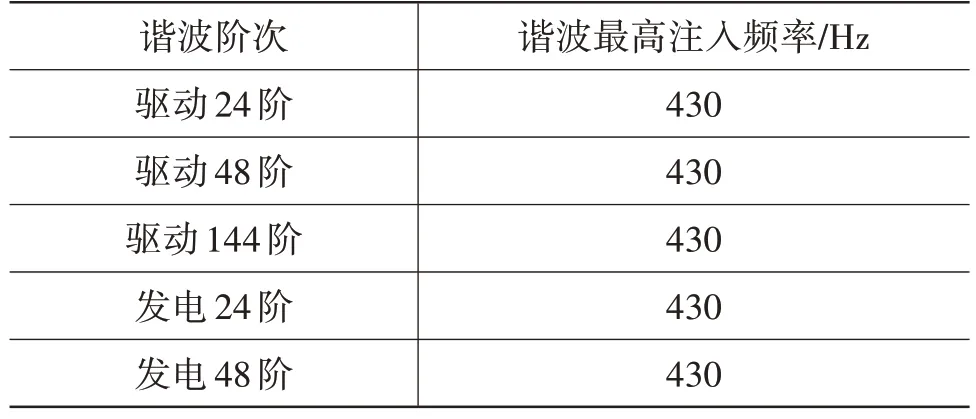
表2 V1.09版动力总成B逆变器控制器软件谐波注入参数

基波运行频率与转速的关系为：

式中，f为基波运行频率；n为电机转速；P=4为极对数。

由试验数据分析可知，单体电芯电压跳变问题出现在电机转速为4 000~6 000 r/min 的区间，根据式（12）可以计算出此转速区间基波运行频率为266.67~400.00 Hz。逆变器谐波注入的6 倍和12 倍频电流频率范围为1.6~4.8 kHz，因此谐波注入的频率与整车电网络系统谐振点2.6 kHz重合，谐波电流幅值被放大，故6 倍频和12 倍频的谐波含量增大，导致母线电压和单体电芯电压跳变，如图6所示。

图6 V1.09版逆变器软件直流母线电流电压波形

选取该段数据中电流最大的一段进行FFT频谱分析，结果如图7所示，此时电机转速约为5 650 r/min，根据式（12）可得此时基波频率约为376.7 Hz，从图7中可以看出，该段数据6倍频（2 260 Hz/367.7 Hz≈6）电流谐波得到显著增强，同时，处于谐振区的谐波明显得到加强。

图7 V1.09版逆变器软件母线电压和电流幅频特性

3.2 优化后逆变器软件谐波注入参数

谐波注入频率与谐振点重合，谐波电流幅值被放大，导致母线电流和单体电芯电压跳变，因此，需要优化逆变器软件谐波注入的频率范围，避开整车电网络系统存在的固有谐振点，优化后V1.10 版软件谐波注入参数如表3所示。

表3 V1.10版动力总成B逆变器控制器软件谐波注入参数

新的谐波注入频率参数不仅谐波注入含量降低，且最高6倍谐波注入频率为2.5 kHz，未达到谐振点2.6 kHz，基本避免了与整车电网络系统谐振点重合，优化了单体电芯电压跳变的幅值，如图8所示。

图8 V1.10版逆变器控制器软件直流母线电流电压波形

对该段数据同样选取电流最大的一段进行FFT频谱分析，结果如图9 所示，此时电机转速约为5 800 r/min，根据式（12）可以计算出此时基波频率约为386.7 Hz。从图9 中可以看出，较优化前，该段数据6倍频和谐振区电流谐波明显改善。

图9 V1.10版逆变器软件母线电压和电流幅频特性

3.3 实车验证

使用V1.10 版本逆变器软件进行实车交叉验证，测试电池包单体电芯电压跳变并观察新的谐波注入参数是否会对整车其他性能如NVH、扭矩响应速度、扭矩控制精度等产生负面影响，电压跳变验证结果如表4所示。

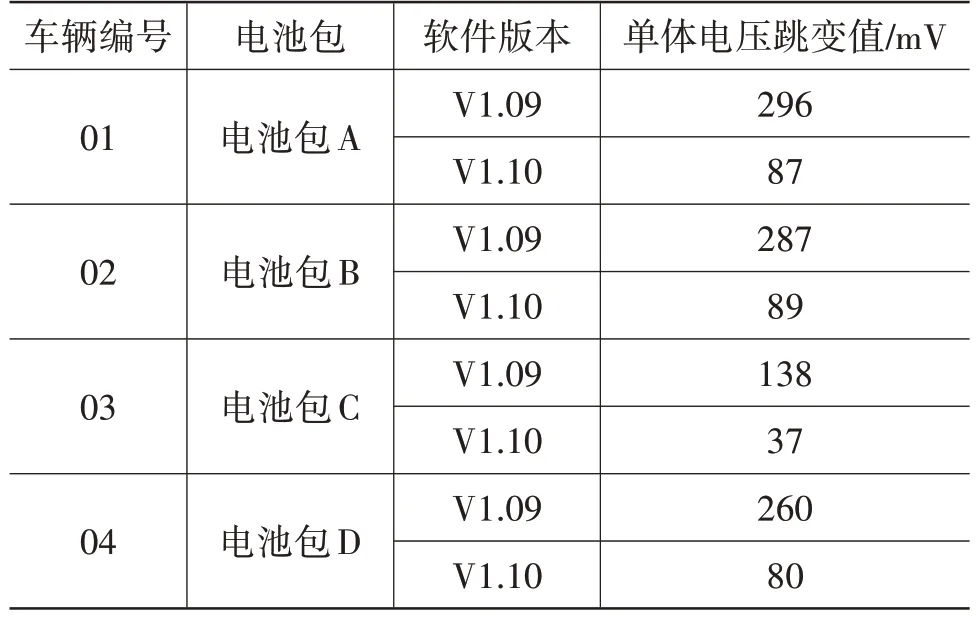
表4 电压跳变验证结果

从表4中可以看出，V1.10版软件可以很好地抑制单体电压跳变。同时，试验中没有新增NVH 和驾驶性相关问题，问题得到解决。

4 结束语

纯电动汽车电池包单体电芯电压跳变问题，多从BMS 软硬件和电芯一致性方向入手分析解决，本文针对某纯电动车型单体电芯电压跳变过大问题，排除相关可能性后，通过多次测试，将原因锁定为逆变器谐波注入参数不合理引发整车电网络系统谐振。通过建立整车电网络模型，计算整车电网络系统谐振点，并对谐波注入策略进行优化，实车试验结果表明该优化策略有效，并得到以下结论：

a.谐波注入方法在电机控制中应用时，需要考虑其对纯电动汽车三电系统其他部件的影响；

b.不同的谐波注入参数对于纯电动汽车各方面性能的影响不同，在开发前期，应根据整车电网络系统的特性选择合适的谐波注入参数，以避免不必要的问题发生。