基于MATLAB的室温分布监测可视化技术

孟祥来

(杭州华电华源环境工程有限公司,湖北 武汉 430044)

0 引言

室温分布监测多用于大型空间区域温度控制,目前的室温监测多选用定点监测或采用二维平面插值进行面监测,其次是模拟仿真技术研究较多,尚未查阅到三维温度可视化监测技术,其难点在于监测温度点的三维插值及四维图的呈现。

肖雪鹏等人在研究中指出:温室自身的结构特点导致其内部温度分布并不均匀,在不同区域的温度存在相对较大的差异,了解温室内部温度分布情况对于优化温室结构、调控温室环境具有重要的意义。在传感器采样的基础上对数据插值,对比不同插值数据数量对温度分布图像的影响,选择出适宜的插值数据数量,利用插值结果与传感器采集数据对比计算误差,并通过实际运算测试不同插值方法的运算速度和数据图像化结果[1]。秦书松等人通过构建矩阵形式的管网模型,在线性化求解过程中采用温度插值策略,实现系统仿真预演,为运行参数优化提供理论支撑[2]。宋德萱等人选取上海市一处地下空间在冬季阴天和晴日进行两次温度测试,将测点温度平均值运用Surfer软件进行插值计算绘制温度等值线图,比较11种插值法的计算性能。得出该教学楼地下空间温度分布插值的最合理方法是反距离加权插值法[3]。

1 实验设备介绍

当前空调系统送风末端领域鲜有准确测量温度分布的测试方法,对于温度分布监测的可视化技术更加少见,主要难点集中在温度测取点布置、温度精确测试仪器选取、测量数据的多维度插值和四维可视化的实现[4]。

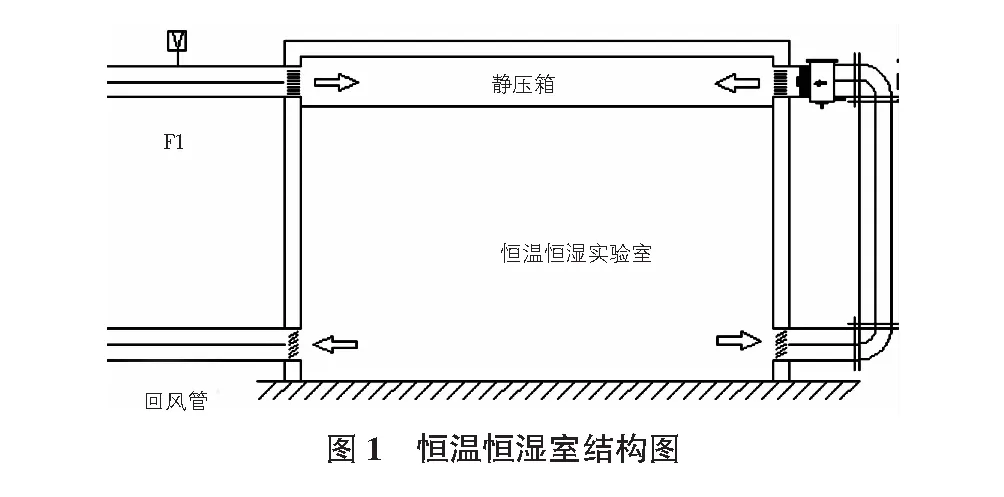
恒温恒湿室作为本次实验对象,总面积为25 m2,围护结构采用双面隔热彩钢库板制作,库板厚度为150 mm,长宽高尺寸分别为6 000 mm,3 500 mm,3 080 mm,如图1所示。恒温恒湿室内设有静压室,位于室内最顶部,高度为470 mm。室温20 ℃时,设计最大冷负荷为12 kW,围护结构负荷为3.25 kW,温度调节范围-25 ℃～55 ℃。恒温恒湿室墙壁处挂有冷风机组,主要用于-25 ℃～10 ℃ 的低温需求。在本文中不作使用,但是其存在会影响恒温恒湿室的温度分布情况。

温度传感器全部采用四线制热电阻,分度号PT100(A),测量精度0.2 ℃。在实际测量中,信号传输线的长度普遍在10 m以上,线路的阻值对二线制热电阻测温会产生较大的影响,测量误差波动较大。四线制热电阻不仅可以消除引出线电阻的影响,还可以消除连接导线间接触电阻及其阻值变化的影响,主要用在高精度温度测量方面。

数据采集仪器选用了一台Agilent 34980A数据采集主机和两块34921衔铁式多路复用器(配有34921T接线模块),通过以太网与PC连接,PC上安装的Agilent BenchLink Data Logger软件可以对数据进行采集和记录。

选用了上海美乐柯制冷设备有限公司的三工况风冷热泵主机一台,制冷量40 kW。

2 送风量和孔板规格的计算

恒温恒湿室作为冰蓄冷空调的负荷端,其内的湿度和温度分布、风速是检验空调系统舒适性的重要指标。恒温恒湿室对于温度场的均匀性要求较高,所以选用全面孔板单向流的送风方式,保证了室内温度分布的均匀性,且不产生回旋气流。孔眼处的送风速度对送风的均匀性有显著影响,当送风速度较大时,稳压层中静压变化对送风速度影响较小[5]。但是,送风速度大于7 m/s～8 m/s时,孔口会产生噪声。因此本实验选取送风速度为4.5 m/s。

恒温恒湿室送风量按夏季最大室内冷负荷计算[6],计算如式(1):

(1)

其中,L为室内送风量,m3/h;Q为室内总显冷负荷,kW;ρ为空气密度,kg/m3;c为空气定压比热容,kJ/(kg·℃);tn为室内温度,℃;ts为送风温度,℃。

孔板孔眼净面积计算如式(2):

(2)

其中,vs为送风速度,m/s;α为流量系数,一般取0.74～0.82。

孔板孔眼的直径取8 mm,孔眼的中心间距通过计算为39.31 mm,实际取40 mm。

孔眼数量的计算见式(3):

(3)

其中,A为孔板面积,m2;Cm为孔眼面积与孔板面积之比,计算值0.032 52;ds为孔眼之间的中心距,mm。

孔板稳压层净高计算见式(4):

(4)

其中,Ls为按空调房间面积计算的单位风量,m3/(m2·h);S为稳压层中孔板部分的气流最大流程,m;vs为送风速度,m/s。

3 温度分布测取

本次试验在恒温恒湿室内布置27个温度测点,沿高度方向上共三层,每层9个,室内高度为210 cm,平均划分3层,传感器布置高度(距离室内地面)分别为52.5 cm,105 cm,157.5 cm。27个测点总共分三次测量(受制于传感器数量,室内只有10个传感器),每次测量一层,测量通道对应安捷伦数据采集仪上的1001—1009通道。同时测量空气处理机组的送风温度,对应通道为1012。

测量的步骤:首先布置157.5 cm高度层面上的9个测点(俯视平面图如图2所示),均匀分布。在Agilent BenchLink Data Logger软件上勾选1001—1009和1012通道,采集数据的时间间隔为5 s,采集数据类型为温度(四线制热电阻),送风温度设定为12 ℃,开始测量。待测量数据平稳并在12 ℃附近波动时持续5 min左右,停止测量。105 cm和52.5 cm高度层上的测量步骤同上。

对恒温恒湿室温度场的测定思路:设定同一送风温度,选取室内温度恒定时段,对各温度测点测取数据取平均值。从170 s至480 s的时段内,室内的9个温度测点测量的温度基本保持稳定,因此,选择此时段来进行计算取平均值。对于105 cm高度层的温度测量结果来看,120 s～400 s的时段内温度保持稳定,没有大的起伏。对于157.5 cm高度层的温度测量结果,在整个测量时段内温度都比较稳定,所以选取了整个测量时段来求温度的平均值。

恒温恒湿室在52.5 cm,105 cm,157.5 cm高度层上的温度测量结果的平均值如表1所示,三个高度层所对应采集数据时刻送风温度的平均值分别为:11.75 ℃,11.82 ℃,11.83 ℃。

4 基于MATLAB的温度场可视化

通过MATLAB软件对恒温恒湿室的三个不同高度层面进行建模,通过无限细化的三维矩阵来模拟出室内在温度传感器层面上的温度分布情况。然后对测量温度值进行插值得到三维矩阵的实际分布值,借助MATLAB的绘图功能来显示温度场的三维分布。

MATLAB二维数据内插值格式为:

ZI=interp2(X,Y,Z,Xi,Yi)。

返回矩阵ZI,其元素包含对应于参量Xi与Yi(可以是向量、或同型矩阵)的元素,即Zi(i,j),[Xi(i,j),Yi(i,j)]。可以输入行向量和列向量Xi与Yi,此时,输出向量Zi与矩阵meshgrid(xi,yi)是同型的。同时取决于由输入矩阵X,Y与Z确定的二维函数Z=f(X,Y)。参量X与Y必须是单调的,且相同的划分格式,就像由命令meshgrid生成的一样。若Xi与Yi中有在X与Y范围之外的点,则相应地返回nan[7]。

网格数据由形成网格的等间距点上的值或测量值组成。网格数据应用于许多领域,如气象学、测绘学和医学成像。在这些领域,经常以固定空间间隔取测量值,且可能随时间进行测量。这些有序的数据网格的范围可以从一维到四维或更高维。griddedInterpolant对象支持对ndgrid格式的数据进行任意维数的插值。这些对象还支持多值插值,其中每个网格点可以有多个关联的值。与使用interp函数相比,使用griddedInterpolant对象具有内存和性能优势。griddedInterpolant为插值对象的重复查询提供了显著的性能改进,而interp函数在每次调用时都会执行新计算。此外,griddedInterpolant以内存高效格式存储采样点,并以多线程方式利用多核计算机处理器。

首先对采集的温度数据和温度传感器的布置位置进行三维建模,一二维表示传感器的平面坐标,第三维表示采集的温度值。以恒温恒湿室52.5 cm高度层面为例,三维矩阵建模如下:

x=[80,160,240];

y=[142.5,285,427.5];

z=[11.90 11.96 12.04;

11.95 11.94 12.07;

11.95 12.05 12.093]。

然后利用[X,Y]=meshgrid(xgv,ygv)的函数生成网格采样点,此处设定在恒温恒湿室长宽方向上的采样步长都为1 cm。生成的网格矩阵如下:

[xi,yi]=meshgrid(0∶320,0∶570)。

在实际的温度变化是连续的,因此在得到的温度场中通过任意点的截面截出的曲线必然是连续可导的,故而必须使用三次样条插值法(spline)可以得到光滑的插值分布曲线。又因为该温度场是在传感器层面上的温度分布,所以使用二维插值函数(interp2)来完成插值。第三维的高度值的变化和连续变化的颜色来显示温度的连续变化。编程实现如下:

zi=interp2(x,y,z,xi,yi,′spline′)。

最后通过三维网格图绘制函数mesh和等高线绘制函数contour来实现温度场的分布图和等高线图:

mesh(xi,yi,zi);

[c,h]=contour(x,y,z)。

恒温恒湿室105 cm,157.5 cm高度层面的温度场和等高线绘制方法也如上所述。

在绘制的三维温度场分布图中,z轴的变化和网格颜色的变化是一致的,为了方便全面展示各高度层面上的温度场分布情况,选择了XY平面视图。三维网格线图XY视图可以全面展示温度的分布情况,在此等高线图不进行展示。

恒温恒湿室52.5 cm,105 cm,157.5 cm高度层的温度场分布的MATLAB实现分别如图3—图5所示。

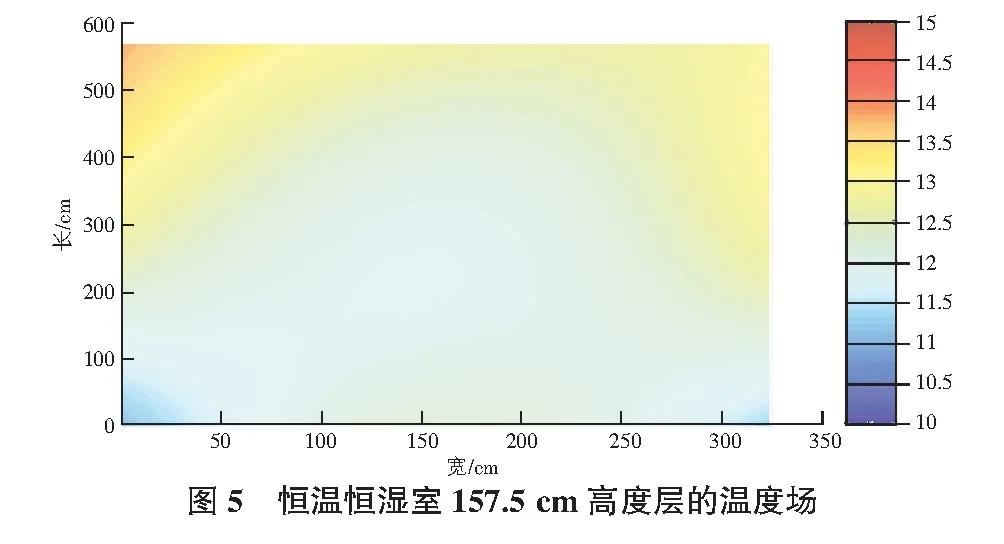
图3—图5可以直观地展示恒温恒湿室内三个不同高度层的平面温度分布情况,但是对室内整个空间的温度呈现并不全面。本节将借助MATLAB提供的四维可视化功能,通过27个测点温度进行相关的数据插值和拟合,立体呈现出室内温度的分布情况。

MATLAB提供的立体可视化函数用于绘制复杂的立体和向量对象,这些函数被用来在三维空间中构建标量或者向量的图形。函数的构建中需要三维数组作为输入参数,三维数组的每一维代表一个坐标轴。如果绘制的函数是一个标量函数,则绘制函数需要四个三维数组,其中三个各代表一个空间坐标轴,第四个数组代表前三组坐标下的标量数据。

恒温恒湿室的温度场的四维可视化首先确定各传感器位置坐标作为前三个数组,温度值作为第四维数组。MATLAB中的slice(X,Y,Z,V,Sx,Sy,Sz)函数可以实现三元函数V=V(X,Y,Z)确定的四维体在三维坐标XZY轴方向上若干点的切片图,这些若干点由参量向量Sx,Sy,Sz确定坐标,这些点对应着若干个平面,即若函数V=V(X,Y,Z)中有一变量如X取一定值X0,则函数V=V(X0,Y,Z)变成一立体曲面,由于将该曲面通过颜色表示温度V,从而显示于一平面。参量X,Y与Z必须有单调的正交的间隔,在每一点上的颜色由对函数V的三维内插值确定。

绘制恒温恒湿室温度场时首先输入坐标数据和与三维坐标对应的温度值,温度V是一个三维数组,应该按照三维数组的方式进行输入。其次对恒温恒湿室的空间进行立体网格划分,建立采样点,调用meshgrid函数,在长宽高方向上各划分50等份,用linspace函数来控制。由于温度和坐标数据属于离散数据,无法直接调用slice函数,所以要建立X,Y,Z,V之间的函数关系,此处调用了网格点插值函数griddedInterpolant。建立坐标数组与温度数组之间的函数插值关系式,插值方法为三次样条插值(spline)。最后通过切片函数slice绘制出恒温恒湿室的四维图形,调用shading interp函数进行色彩插值,平滑色彩过渡。最终绘制结果如图6所示。

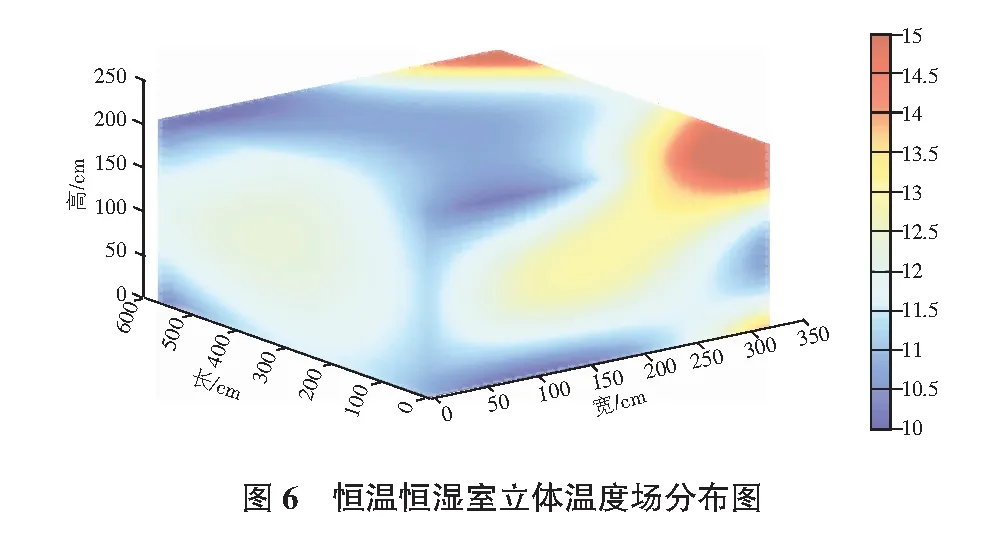
图6显示恒温恒湿室内中部温度分布均匀,普遍维持在12 ℃左右,顶部空间温度略低,主要由于此处为送孔板处,温度与送风温度接近。高温部分出现在后部两顶点处,这个区域在实际测量中温度确实偏高,此处布置了两组冷风机(停用状态),阻碍了空气的对流换热,使得此处温度短时间内很难下降。

5 结论

本文借助实验和计算机建模的方式,实现了室内温度分布监测的可视化,提供了孔板式送风的设计方式、MATLAB在温度分布上的二维、三维插值方法、MATLAB在温度分布上的三维、四维的绘图方法,为室温分布监测的可视化技术提供了解决方案。