基于线段拓扑关系的轮廓偏置算法

胡平山 丁浩亮 冯漾漾 严 波

1.上海交通大学材料科学与工程学院,上海,2000302.航天材料及工艺研究所,北京,100076

0 引言

曲线的偏置操作常用于复杂型面的工装模具设计[1]、数控加工的刀轨控制[2-3]、智能机器人的行走路径规划[4]等领域。在增材制造过程中,偏置线段是无交叉无重叠的连续线段,与平行线扫描方式相比能保持加工过程的连续,扫描效率更高,并能解决边界处台阶效应。因此研究合适的增材制造路径规划策略,能使零件成形精度更高和表面质量更佳[5-6],并能影响加工过程温度场和应力场分布,决定成形零件的力学性能。但针对复杂零件的高效且稳定的轮廓偏置算法一直是增材制造路径规划研究的难点。

当前偏置算法包括图形算法和图像算法两类。图形算法基于拓扑关系的线段偏置[7],利用有向线段的集合表征自由曲线,通过线段端点的偏置来控制线段的移动。YANG等[8]提出利用截面边界进行偏置得到填充线段的方法,对重叠部分进行合并,对尖锐顶点进行特殊处理,与光栅式扫描相比,扫描时间和零件表面质量均得到了改善。ELBER[9]通过分析偏置线段是否发生反向来判断曲线的局部自交。LEE等[10]使用圆环沿基曲线扫掠,计算圆环是否和基曲线发生干涉来检测是否发生自交。PERSON[11]提出子区域划分法Voronoi图法,将平面区域划分成多个子区域,之后在子区域中进行偏置,避免了复杂的互交判断。FELKEL等[12]提出通过多边形的拓扑骨架来分析几何形状,并利用骨架的等分线计算区域的偏置填充曲线,完全回避了线段的偏置计算。

图像算法一般基于顶点的离散偏置[13],将原始曲线细分为点集,对每个顶点进行偏置之后将顶点拟合为线段。CHEN[14]将轮廓线离散为点,再进行基于图像的扩张和轮廓环的重新识别,以避免异常问题,算法具有很好的稳定性。李俊杰[1]通过在原始线段上选取参考点并利用渐进迭代的方式获取偏置轨迹。JIN等[15]利用非均匀有理B样条曲线对偏置扫描路径进行拟合,进一步提高偏置边界的精度和加工产品的表面质量。

以上两种算法各有优劣:图形算法的优势在于方法直观,运行效率高,而缺点便是需要处理复杂的相交情况;图像算法则能更加鲁棒地实现偏置,避免异常情况的处理,但运行速度缓慢,且在轮廓复杂区域难以正确高效处理小环路径。

针对复杂零件,本文提出一种基于线段拓扑关系的轮廓偏置算法,研究对偏置算法稳定性影响较大的环相交问题和尖角问题,并进行了实验验证。

1 偏置算法模型

1.1 总体框架

算法的基本原理是:对于经切片处理得到的简单填充区域,由一个外环和若干内环组成,实现外环的向内偏置更新,依次处理环的相交和干涉异常情况,得到无重叠无干涉的有效路径环,进行环的光顺处理消除路径上的极端尖角,提高算法的稳定性,重复以上过程直到区域完全填充,算法流程如图1所示。

1.2 偏置异常处理

由于曲线形状的复杂性,偏置结果常常包含环的相交,一方面会导致轮廓的失真,成形件的表面特征缺失,另一方面会出现内部填充的欠熔覆和过熔覆问题,影响零件力学性能,更严重的是使曲线偏离正常拓扑关系,算法计算出现失稳和崩溃。因此需要对偏置异常情况进行分析,提出基于线段拓扑的多环处理算法流程,如图2所示。

图2 偏置异常处理流程图

1.2.1环相交的形成机理

目前大多数理论证明环的相交是由于曲线局部曲率小于偏置距离,边界发生翻转造成的干涉现象。对偏置过程中线段端点的移动进行数学建模,研究偏置过程中端点的移动如何影响线段的空间拓扑关系。

图3定义直线和相邻两直线的夹角分别为θ和α,线段偏置距离为H,左右两端点分别为PL和PR,其中PR经过偏置之后得到P′R,而线段的长度记为L,由于两端点移动的差异,线段的长度发生变化。

图3 线段相交数学分析

由几何关系可以得到右端点在直线方向上的相对移动距离:

(1)

同理计算左端点的移动距离ΔdL,当两者的移动距离之和大于线段长度L即

ΔdR+ΔdL>L

(2)

时,线段偏置后反向。

考虑线段的方向,定义沿环方向相邻两线段方向向量的偏转为逆时针时,两线段之间的夹角角度是正值,此时PR的偏置点为向左移动,ΔdR为正值;而沿环方向相邻两线段方向向量的偏转为顺时针的线段夹角角度为负值,此时PR的偏置点向右移动,ΔdR为负值。在图3中,θ和α均为正值,式(2)可以调整为左右两端点移动的相对距离绝对值:

(3)

如图4所示,将满足线段发生翻转分为两种,计算相邻线段的夹角θ和α,当相邻线段的方向向量叉乘为正时夹角为正值,叉乘为负时夹角为负值。当相邻两线段的偏转方向相同时,目标线段如果发生翻转,相邻线段会提前相交,在局部形成自交环,如图4a所示。当相邻两线段的偏转方向相反时,目标线段如果发生翻转,相邻线段仍然经过翻转线段后并不会在局部形成自交环,如图4b所示。

1.2.2异常分类和环失效识别

根据异常出现的原因可以大致分为:第一类自交问题、第二类自交问题、干涉问题和特殊相交情形。

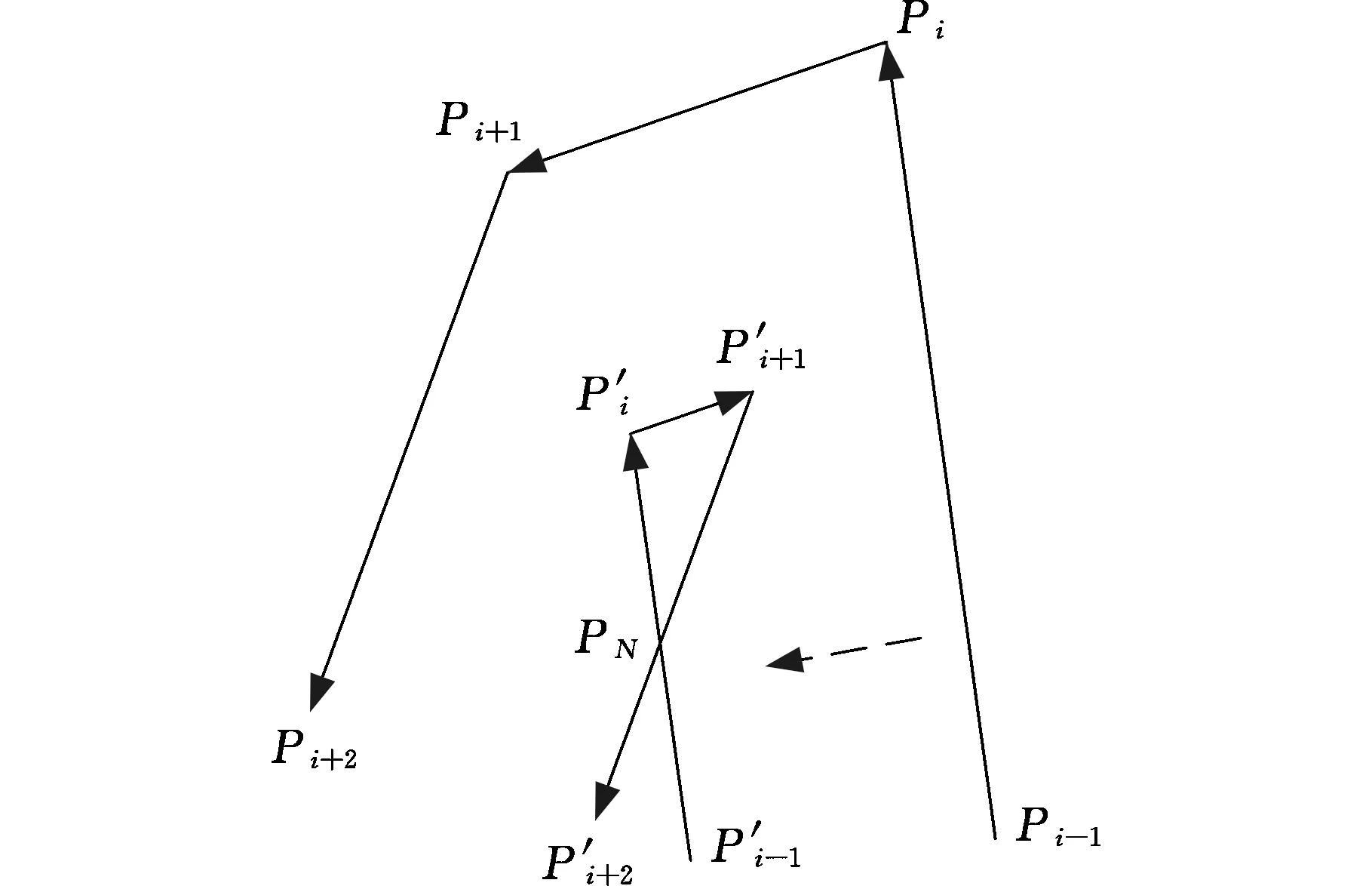
图5 第一类自交异常

第二类自交异常(图6)也称为全局自交,是两条不相邻线段的最小距离小于偏置距离,在偏置之后出现相互干涉的情况。

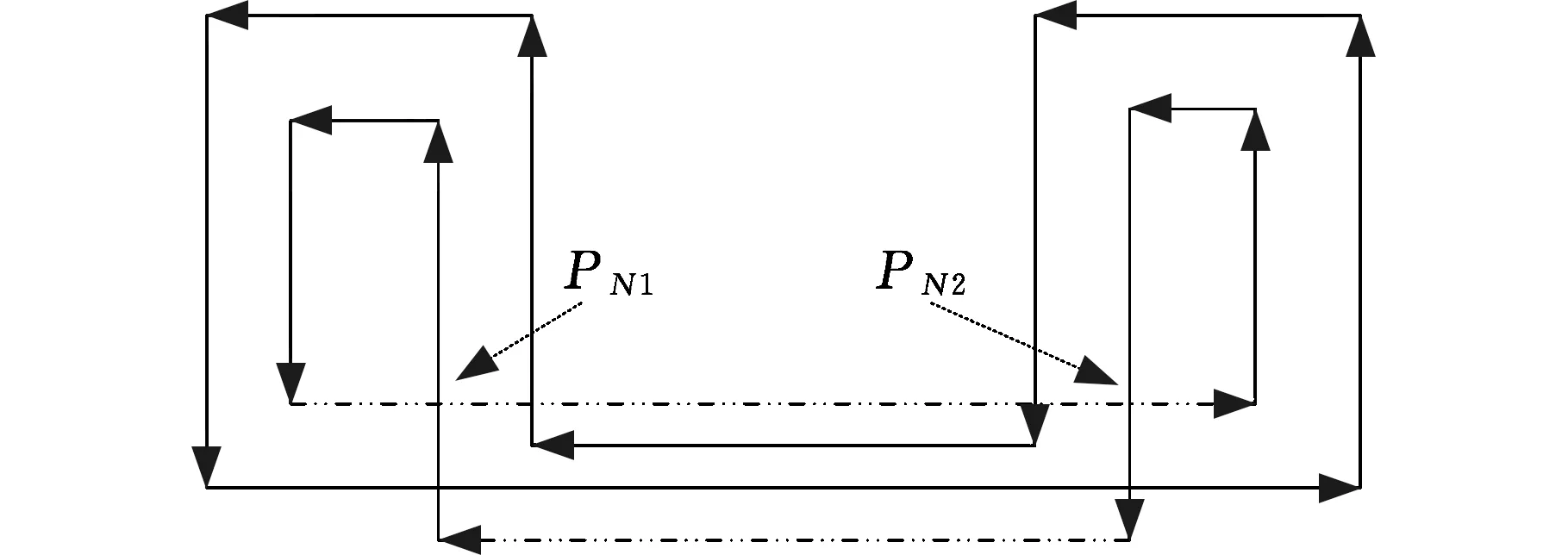
图6 第二类自交异常

干涉问题(图7)。对于复杂的图形边界,当外环(实线)向内不断偏置,到达某一时刻和内环(虚线)发生相交,内环边界成为外环边界的一部分。

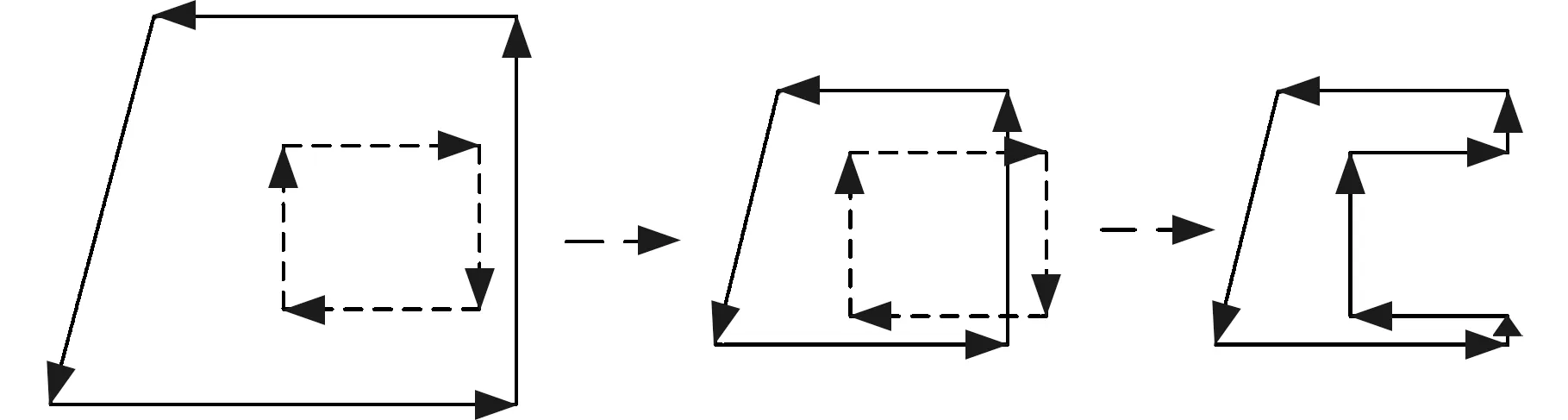
(a)偏置前 (b)偏置中 (c)偏置后

特殊相交(图8):在复杂局部特征的偏置中,局部区域的线段长度与偏置距离相比较小,导致多条线段的多次翻转。图8所示两环均是逆时针方向,其中被包含的环为无效环。

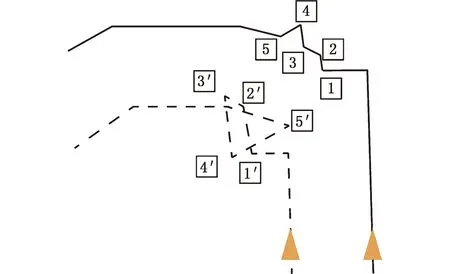
图8 特殊情形

通过以上分类讨论,确定了每种异常的产生原因和特点,设计了相应的环失效判据:

(1)由于当前操作的环为外环,初始旋向为逆时针,因此,若识别目标的旋转方向为顺时针则属于异常分类中的前三类。

(2)理想的边界为无相交无干涉的外环,通过判断当前区域内环的包含关系,被包含的环属于异常分类中的第四类。

(3)计算环内坐标值得最大值和最小值,面积过小的环形区域为冗余加工区域。

1.3 偏置尖角问题

实际的图形边界复杂多样,往往是许多的短线段连接而成,相邻短线段斜率可能相近,也可能相差很大,如图9中Ⅰ、Ⅱ两区域中所示。Ⅰ区域的直线是由一系列斜率相近的短线段连接而成,Ⅱ区域在局部出现相邻线段的方向接近相反而构成尖角特征,导致在激光加工时出现冗余行程。

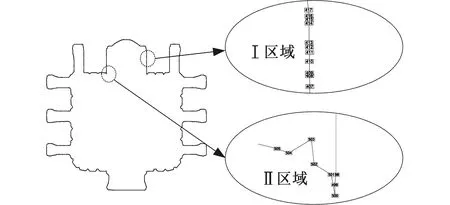
图9 未光顺化的边界

1.3.1尖角对算法稳定性的影响分析

算法稳定性是偏置算法设计的首要目标,需要保证算法在任何情形下均能保持计算的合理性以及结果的可靠性。在图3中,顶点PR到P′R的移动距离Δd可以使用偏置距离H和邻边的夹角θ表示:

Δd=H/cos(0.5θ)

(6)

将顶点偏置距离和夹角的关系表示为表1,可以发现随着偏转角度的增大,Δd会急剧增大。

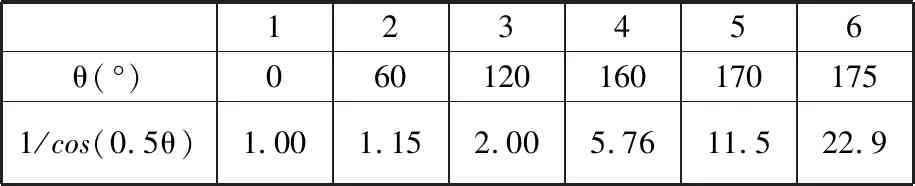
表1 顶点偏置距离和偏置夹角关系

图10和图11所示分别为原始图形(图9)经过一次偏置和两次偏置后的结果,可以发现图9中的尖角被区域偏置后逐渐放大,而在偏置过程中形成的极端尖角会在图11中造成偏置过程的崩溃。

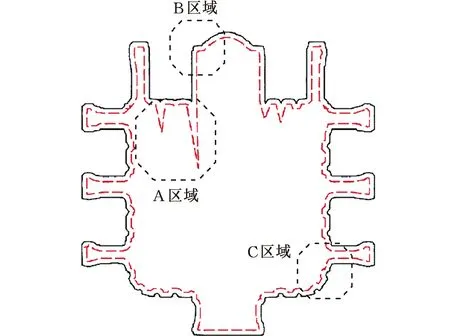
图10 第一次偏置结果

图11 第二次偏置结果

图10尖角特征的形成机理可以分为图中所示A、B、C区域中的三种情形。

A区域中的尖角特征来自基线上已经存在的特征,如图9中局部放大图所示,此区域相邻线段偏转角度约170°,由表1可知该顶点的偏置距离大概为线段偏置距离H的11.5倍,从而在偏置线局部形成放大后的尖角。

B区域的局部放大如图12所示,实线为偏置之前的原始线段,虚线为偏置之后的边界线,由于线段P2P3和线段P6P7的翻转,在偏置线上出现极端尖角,符合1.2.1节中提出的相交分析理论,由于左右端点的相对运动,原本偏转角度极小的短线段产生方向的翻转,成为偏转角度极大的尖角。

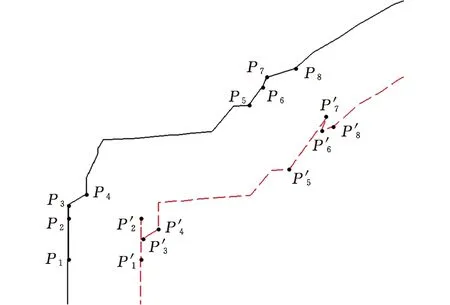
图12 B区域尖角放大图

图13是C区域的局部放大图,实线为偏置前的原始线段,虚线为偏置后的边界线,由于偏置过程中的相交现象导致原本不相邻的线段变成相邻的线段。

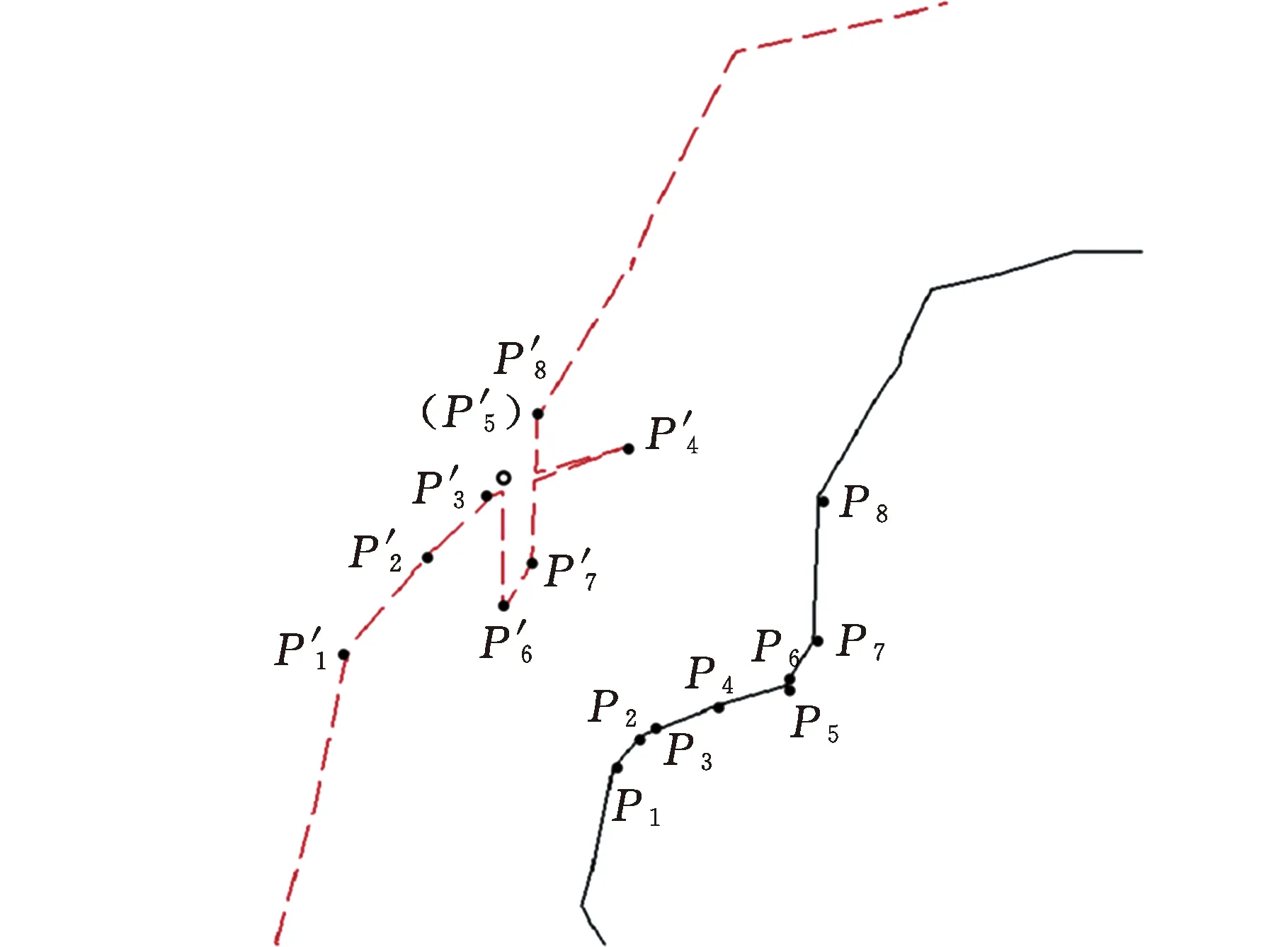
图13 C区域尖角放大图

1.3.2修补式光顺处理

为解决以上尖角问题,提出通过增加线段调整偏转角度的修补式光顺处理方案。如图14所示,当前判断的线段BC与集合中最后的线段AB的夹角为θ,判断超出上边界:

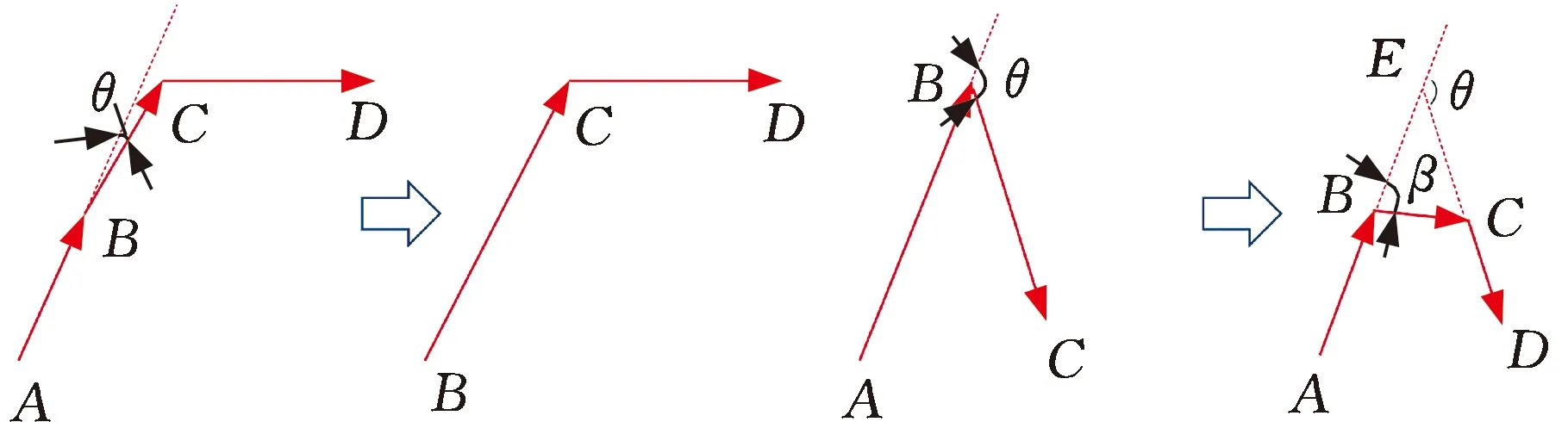
图14 修补式光顺方案

θ≥θmax

(7)

在两线段上取lBE=lCE得到等腰三角形BEC,计算新线段和集合末尾线段AB的夹角:

从而保证了处理后的线段夹角β一定属于合理角度范围β<θmax。

对图9原始数据光顺处理之后再次偏置,得到结果如图15所示,由于修补式光顺方案保证了偏置曲线上任意邻边之间偏转角度θ∈(10°,120°),顶点的偏置距离不超过线段偏置距离的两倍,不会出现图11中过长的移动,保证了算法稳定运行。图16所示为两次偏置的优化结果。

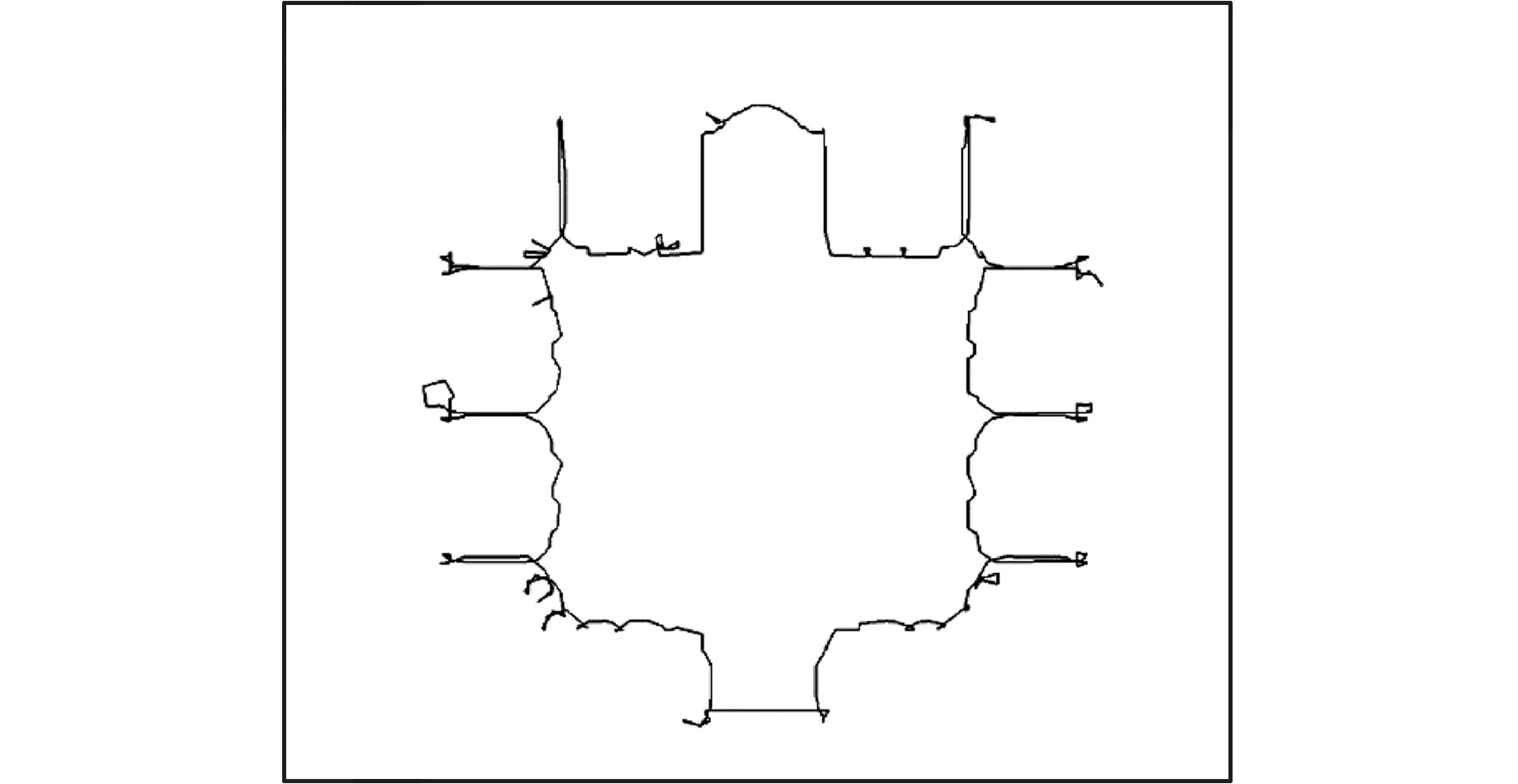
图15 第二次偏置结果(修正后)

图16 最终优化结果

2 算法实例分析

2.1 CGAL几何图形库偏置对比

对于二维曲线的偏置,CGAL几何图形库提供了一种基于多边形骨架的轮廓偏置算法。基于CGAL库编写计算程序对图9进行骨架偏置计算,偏置距离为0.5,得到结果如图17所示。

图17 基于CGAL算法的结果

分析发现,图17中存在以下问题:

(1)路径中存在大量角度变化巨大的相邻线段,造成激光器加工过程中的急停和变向,扫描速度的不均匀影响加工效率,出现粉末过烧。

(2)顶点的移动距离差异较大,填充区域粉末烧结不均匀,会导致零件力学性能降低。

(3)填充区域被分割为多个独立区域,需要增加区域之间的过渡连接线。

采用光顺处理算法对原始曲线进行处理后,再次使用CGAL的骨架轮廓偏置进行计算,并和本文算法计算结果对比,结果如图18所示,分析时间成本如表2所示。

表2 程序运行时间对比

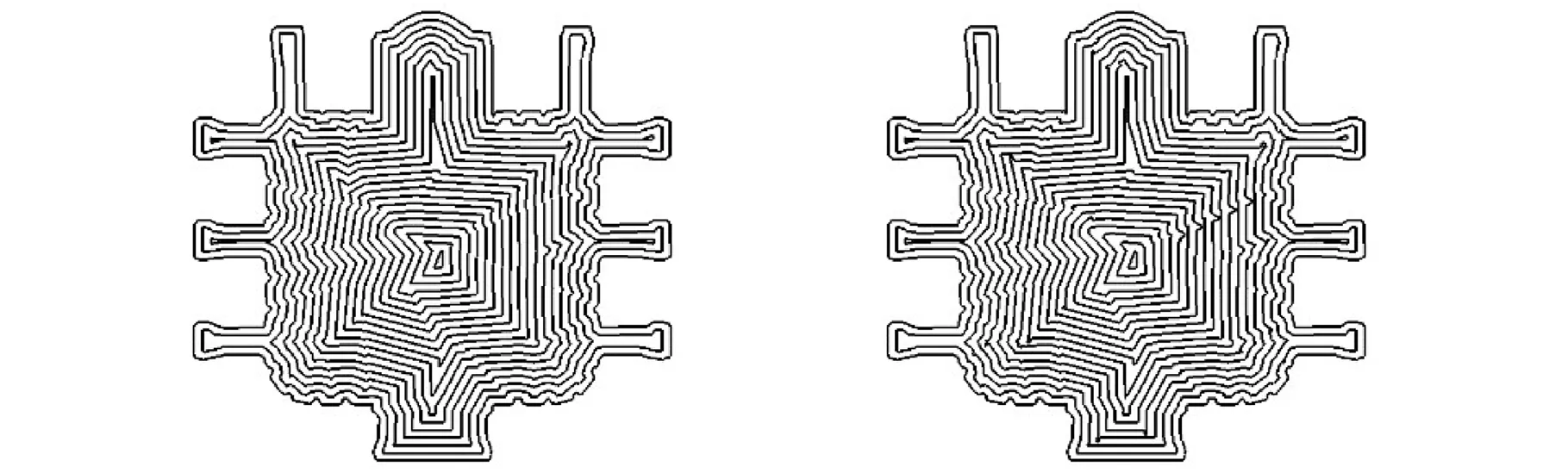
(a)优化的CGAL算法 (b)本文算法

与本文算法的偏置结果进行比较,两者形状基本一致,本质是顶点沿着邻边夹角的角平分线移动,CGAL算法采用更加稠密的计算步长生成骨架,避免了偏置后线段自交的出现,而本文的算法采用固定的偏置距离,离散并简化计算过程,但需要重点研究环自交问题处理。而与CGAL算法的偏置计算时间相比,本文算法具有显著的效率优势,更符合加工需要。

比较图17和图18a中的结果差异,CGAL偏置算法依赖于图形骨架生成,对原始曲线的局部特征非常敏感,偏置结果差异性较大;采用本文光顺化处理算法能优化边界曲线,使生成的骨架更加合理,偏置扫描线更加符合选取激光融化工艺的需求。

2.2 扫描效率分析

目前常用的扫描路径规划方式还有平行线扫描、分区扫描、分形扫描等,根据各自成形特点适用于不同结构特征的零件,因此对平行线扫描(图19)、分区扫描(图20)和轮廓扫描(图21)进行实验对比分析。

(a)全局图 (b)局部放大图

(a)全局图 (b)局部放大图

(a)全局图 (b)局部放大图

平行线扫描是最朴素的扫描方式,沿着某确定的方向顺序填充截面区,并根据扫描线奇偶调整方向进行往返运动扫描,算法简单,容易实现,但激光器会频繁跨越型腔。

分区扫描则是在平行线扫描基础上,按照一定规则将零件截面划分成多个小区域,将每个区域单独规划后依次连接得到整体的扫描路径,解决了平行线扫描频繁跨越型腔的空行程问题,并可以通过在不同小区域采用不同的方向使各向异性和翘曲变形降低。

针对三种扫描路径对上述零件进行实验设计,分别对加工过程中的转弯次数m、启停次数n、打印总长度Ltol进行统计,结果如表3所示。可以看出,平行线扫描方式由于存在跨越型腔的运动,扫描线长度最长,并且激光器需要频繁的启停操作;分区扫描方式将区域划分为简单连通区域,减少了无效行程,扫描线总长度最短,但是存在频繁转弯;而轮廓扫描的扫描线长度较短,同时保持了较少的激光器转弯次数和启停次数,是最优的扫描方式。

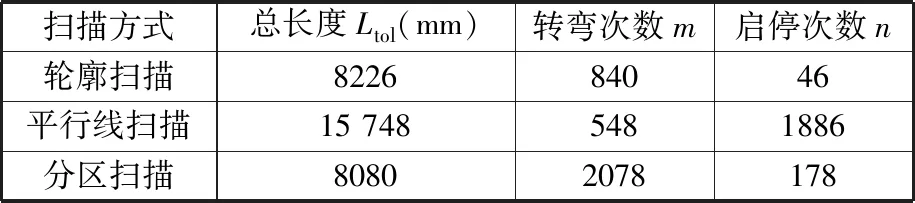
表3 三种扫描方式结果对比

3 结论

本文研究了选区激光熔化的轮廓偏置路径规划算法,从偏置向量的计算、偏置异常情况处理和偏置光顺处理三个方面进行设计,并探究了环相交异常和尖角问题的产生机理,分析其对算法稳定性的影响,并提出相应的解决方法,实现高效稳定的偏置计算。通过实验分析得到以下结论:

(1)与现有的CGAL算法库中偏置算法相比,本文算法结果计算准确,时间成本低,更加符合选区激光熔化工艺需要。

(2)与其他扫描方式相比,本文算法结果的路径长度、转弯次数和启停次数均较低,能保证较高的加工效率。