一种点阵式海上风电机组基础结构水动力稳性研究

朱江峰 曹宇光 赵前坤 李 磊

1.中国石油大学(华东)储运与建筑工程学院,青岛,2665802.山东海洋工程装备研究院有限公司,青岛,266555

0 引言

随着海上风电大功率化和深远海发展趋势,多风机共享平台一体化概念被逐渐提出。LIU等[1]提出了三台风电机组的半潜式整体基础的概念,得出了水动力响应规律和作业工况适应性。VAHID等[2]在2020年建立了可满足33 kW的风能发电的双风电机组浮式平台。ZHU等[3]提出一种满足10 MW发电功率的双风电机组组合的半潜式三角平台。ZHANG等[4]提出了六角箱概念,将养鱼网箱与三台60 kW风电机组相结合,但没有进一步显示实验和现场工程应用分析的结果。

多风机一体化概念虽然被提出,但关于新型结构水动力稳性和传统结构对比并未展开深入研究。在风机系统动力响应分析方法方面,李垚等[5]总结了风电机组可靠性研究的常用方法和提高风电机组可靠性的措施。梁家铭等[6]针对新型网箱水动力分析及系泊方式进行研究,发现新型网箱在工作海况和极端海况均能满足安全性要求。刘宇航等[7]对三种海上风电机组支撑基础与船舶碰撞的动力响应展开分析,结果显示单柱基础海上风电机组位移和加速度响应更加明显。秦大同等[8]对运行工况下风电机组传动系统进行机电耦合建模以及动态特性分析,结果表明传动系统在变速变载状态下的动态响应复杂。彭春江等[9]对海上浮式风电机组刚柔耦合结构进行动力学建模与分析,结果表明波高越大,整机耦合程度越高。

本文针对传统半潜式单风机平台和点阵式多风机一体化基础(DMF)展开分析,明确多风机平台水动力稳性响应规律。本研究基于传统OC4半潜式风机和Windfloat平台结构,考虑满足30 MW级发电需求,设计点阵式六边形风机基础结构,并将数值模拟和水槽实验进行对比分析。

1 点阵式多边形浮式基础参数

本研究结构方案设计参考传统OC4和Windfloat半潜式平台基础,详细参数见图1和表1。选定风机类型均为NREL Baseline 5 MW[10-13],风电机组数量为6个,以点阵式对称排布,相当于点阵式基础风机发电功率为另外两种基础的发电功率的6倍。点阵式基础结构参数与传统半潜式浮式基础的最大不同是浮筒数量和间距。

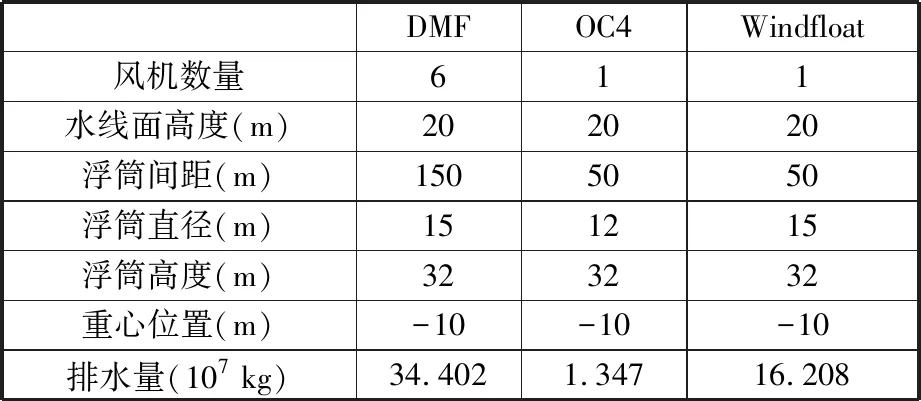
表1 浮式结构基本参数

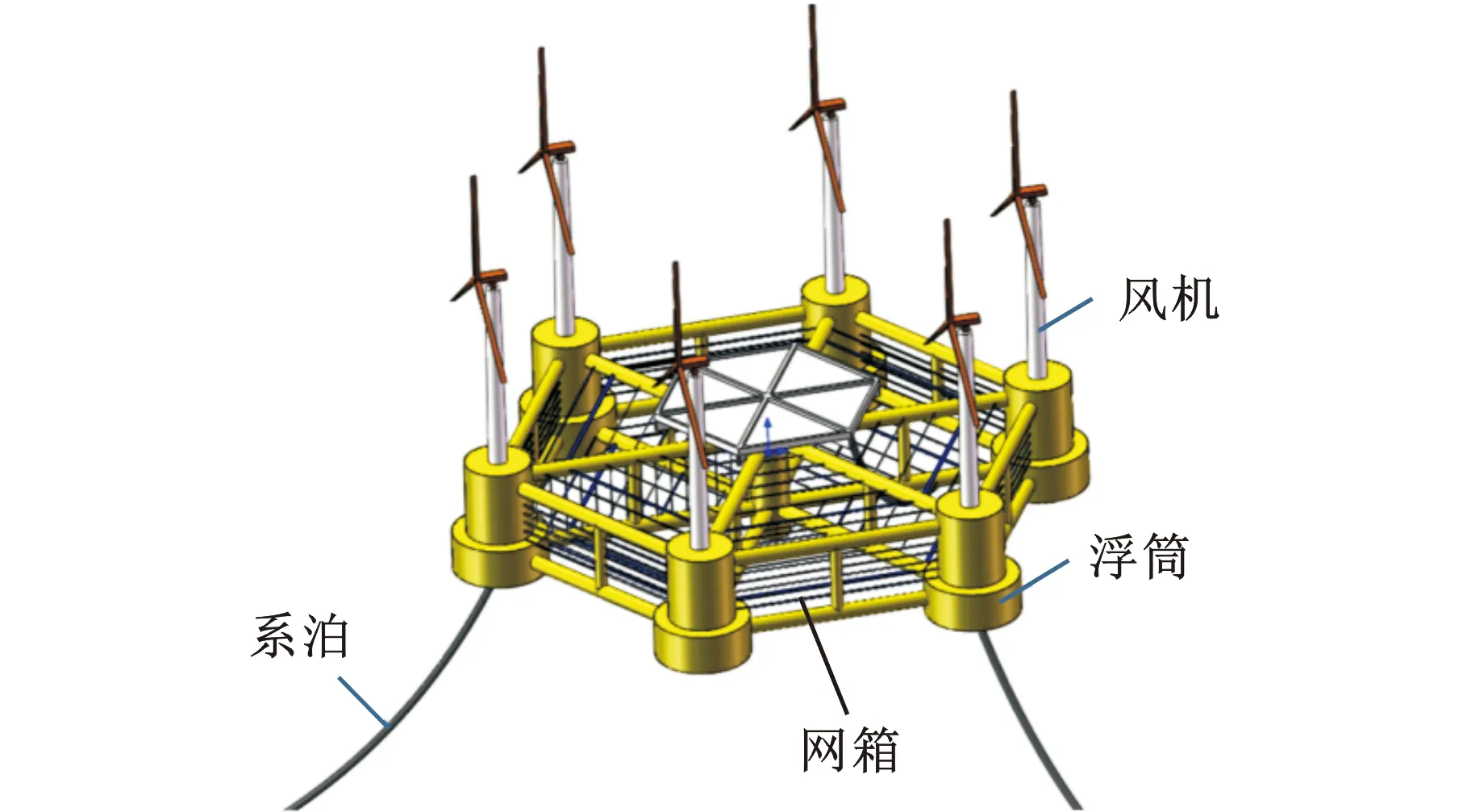
图1 点阵式基础整体概念

2 理论分析

2.1 载荷计算

由于DMF受环境载荷影响复杂,故本文分别考虑风浪流载荷进行分析计算。

(1)风载荷。风载荷对DMF的影响不可忽视。由于本文主要研究风载荷对DMF系统稳性的影响,因此考虑常规作业风作用,基于风机尾流无旋动量理论[14],同时考虑整体结构纵荡和纵摇对风机气动载荷耦合响应,建立风机叶片与塔架水平推力和力矩的公式:

(1)

(2)

式中,ρ为空气密度;vRW为相对风速,满足vRW=vW-vS,vW为实际风速;vS为浮式点阵式基础结构顺风向水平运动速度;CS为形状系数;CH为高度系数;L为风机塔筒高度;A为扫掠面积,正常作业工况为叶片扫掠圆面积2πr,极端风浪载荷工况下叶片为停转状态;vD为纵荡和纵摇引起的相对速度与稳态速度偏差[14]。

(2)浪载荷。波频载荷的计算方法考虑构件截面特征尺度D与波长λ比值,当D/λ≤0.2时为小尺度构件,本研究中网衣、横撑等效为小尺度构件,根据Morison公式计算小尺度构件波频载荷:

F=FD+FI

(3)

式中,FD为拖曳力,由于传统Morison公式主要用于计算水动力固定物,本研究中多风电机组一体化一体结构为海上漂浮物;FI为惯性力。

当D/λ>0.2时为大尺寸构件,在波浪作用下,一般承受惯性力和绕流力,用三维势流理论进行波浪载荷的计算:

(4)

式中,Cdn为法向流阻力系数;α为波浪倾角;Cdt为切向流阻力系数;ρW为液体密度;l为基础平台跨度;d梁结构直径;v0波浪初始速度;v为波速;t为时间;CM为质量系数。

(3)流载荷。流载荷设置为恒定流速,与时间无关,在海洋工程中它的计算满足[11]

(5)

式中,CDC为法向流阻力系数;vRC为相对流速,满足vRC=vC-vS,vC为实际流速。

根据建立的载荷与运动方程,通过理论计算推导出风电机组风力载荷,然后直接将载荷施加到软件模型中进行水动力求解。

2.2 力学模型

基于点阵式基础结构形式的特殊性,结合传统OC4半潜式基础,建立两种浮式基础的力学模型。图2所示为DMF和OC4基础力学模型,二者的纵摇运动主要由风倾力矩和复原力矩的变化引起。

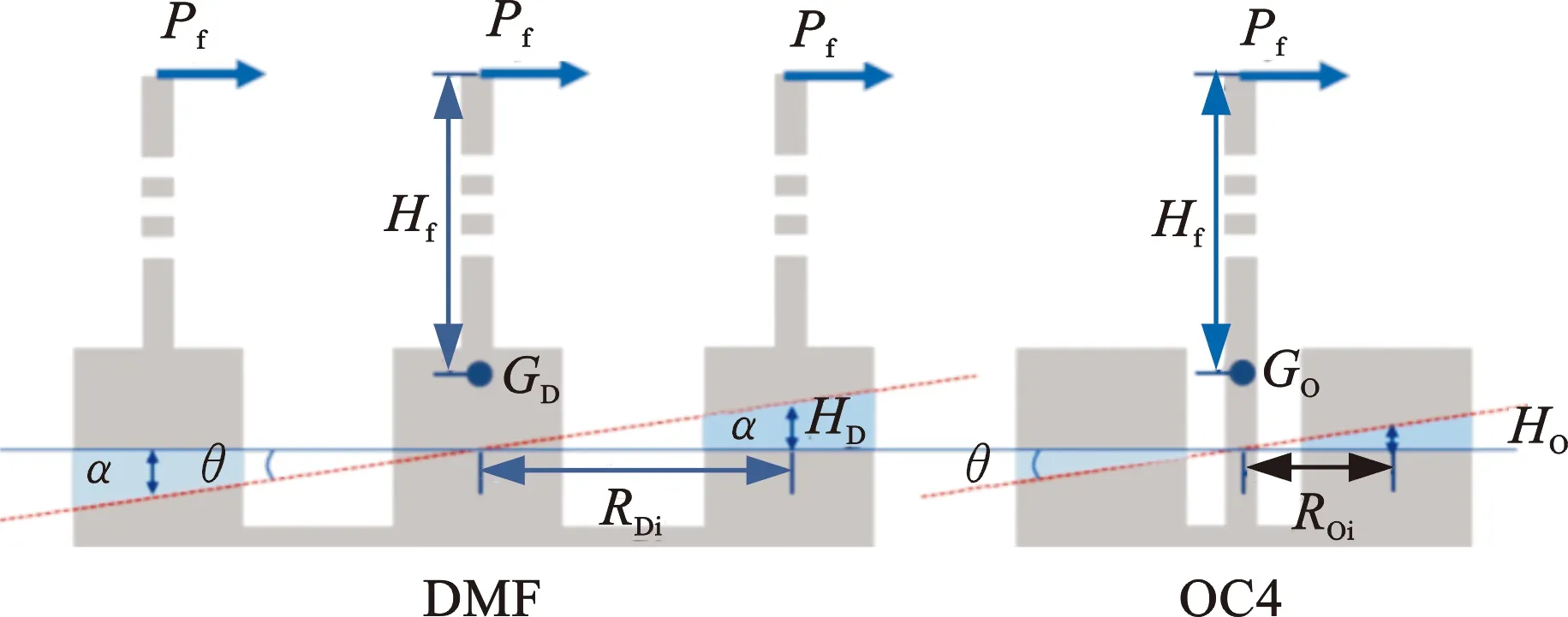
图2 基础力学模型

图2中,DMF的复原力矩满足

(6)

式中,i为风力机编号;n为风力机总量;ρs为海水密度;Si为水线面面积;RDi为水线面与重心的水平距离;θ为整体结构纵摇倾角。

OC4的复原力矩满足

(7)

式中,ROi为OC4水线面与重心的水平距离。

由图2和式(6)、式(7)得,当倾角和水线面不变时,复原力矩与各水线面到重心距离的平方成正比关系,因此通过改变浮体间距可以实现平方级别提高浮式基础的复原力矩。

2.3 运动方程

点阵式一体化结构同时承受风浪流等综合因素影响,因此建立风机-浮筒基础-系泊系统的整体结构分析模型是十分必要的,而载荷模型应该包括空气动力-水动力的耦合模型[15]。浮体在水中的运动形式可分为摇摆和振荡漂移两种,主要受环境载荷对结构产生的力和力矩作用。由于整体结构为刚性连接,为便于分析,首先基于质量集中法,将整体结构等效为一个质量块m0,并考虑结构阻尼、惯性和弹性恢复作用,进行运动方程分析。

浮体摇摆运动方程满足

(8)

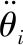
浮体平荡运动方程满足

(9)

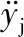
为统一表征浮体摇荡运动与环境作用关系,基于功能守恒定理,建立点阵式一体结构联合运动方程:

Fjyj+Miθi

(10)

考虑系泊系统作用的系泊浮体时域耦合运动方程为

(11)

3 数值模型

利用有限元水动力分析软件ANSYS AQWA对基础的浮筒和撑杆进行水动力模型的构建。为简化计算,设置点阵式多风机系统为刚体结构,其中浮筒的特征尺度和波长比大于0.2,为大尺度构件,建立面元模型,运用三维势流理论计算波浪载荷;撑杆的特征长度与波长的比值均小于0.2,为小尺度构件,建立Morrison杆元模型,风浪流同向,载荷方向为0°。

(1)海况参数。根据IEC 61400—1: 2005的规定[13],风电机组极限载荷取决于50年一遇最大10 min平均风速和极大3S风速。为进一步确保结构的安全性,在选择极端海况时,选择100年一遇的南海极端海况,作业海况则依据NREL公布的5MW风机工作风速确定,具体环境参数如表2所示。

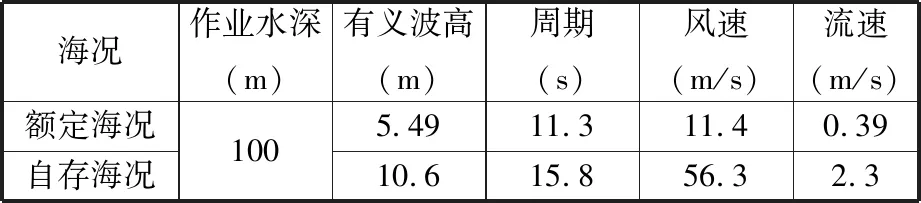
表2 南海环境参数

(2)水动力分析模型。DMF浮式基础坐标依据右手定则,原点选在水面上,与塔架支撑浮筒中心轴相交,z轴竖直向上且与塔架支撑浮筒的中心轴重合,模型整体关于x轴对称。在水平面内,x轴正向与风浪流入射方向的夹角定义为环境载荷的入射角度β,逆时针旋转为正。选用A36海上钢材,泊松比为0.3,屈服极限为450 MPa。海面以上为10 m,海面以下为35 m,整体漂浮于海面,采用六点系泊方法,系泊材料选用聚酯缆[16]。

(3)模型建立与网格划分。利用ANSYS AQWA对基础的海洋多风电机组一体化结构建立水动力模型,网格划分见图3。基于AQWA软件水动力分析建模要求,整体结构采用壳单元;考虑网衣结构复杂性不进行单独建模,网衣承受载荷参照式(3)和式(6)计算得出,直接施加到浮式基础上;风载荷按照式(1)和式(2)计算得出,直接施加到风机塔筒顶端,方向与海流载荷一致,为坐标x轴正方向。

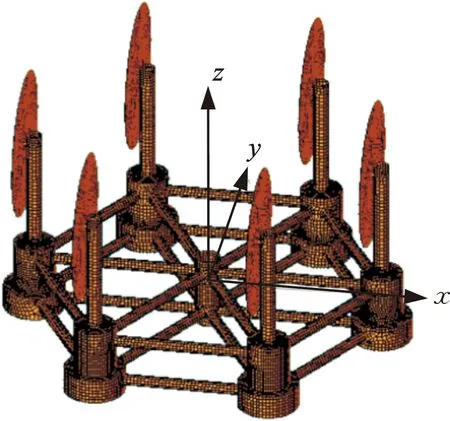
图3 DMF网格划分

4 结果与分析

4.1 模型可靠性验证

利用ANSYS AQWA建立OC4和DWF基础的水动力模型。通过自由衰减运动的数值模拟分别进行纵摇和横荡时域响应对比分析,设置初始倾角为8°,初始水平位移为20 m。该方法不仅可以确定平台固有频率等属性,而且可以验证数值求解器在浮式结构物水动力求解问题上的可靠性。自由衰减模拟结果如图4、图5所示。

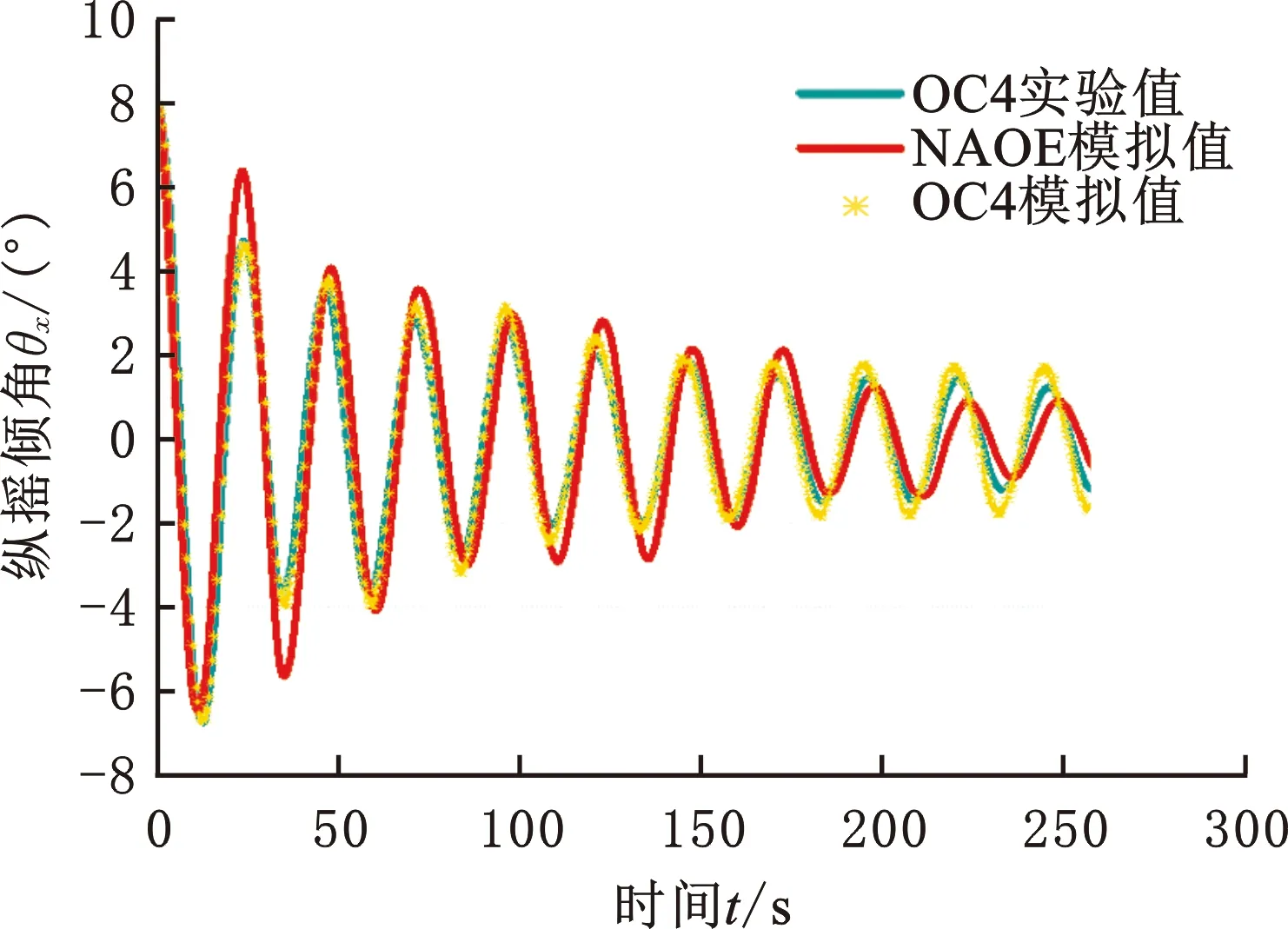
图4 纵摇衰减结果

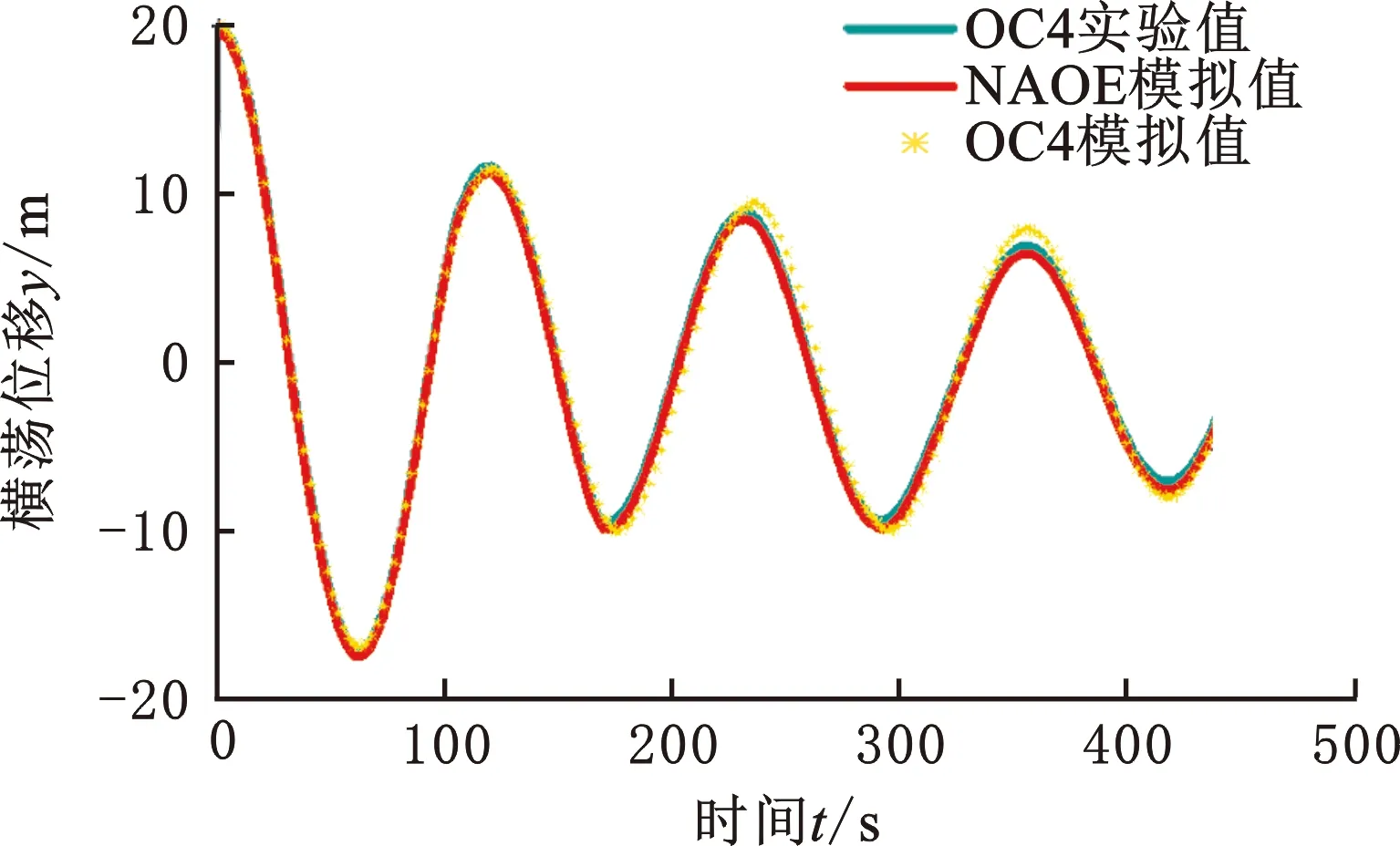
图5 横荡衰减结果

根据图4和图5中可知,模型的固有周期和衰减幅度的预报与文献[17]的浮式风机气动-水动力耦合流场数值模拟和OC4水池试验数据相吻合,最大误差小于5%,证明该求解器在计算该浮式风机支撑平台的水动力问题上具有较好的可靠性与较高的精度。基于AQWA软件得出OC4的纵摇固有周期为26.1 s,与NAEO算法计算的结果25.8 s和OC4水池试验得到的26.8 s周期基本一致。

4.2 风浪流动力响应分析

为明确风浪流因素联合作用对新型DMF基础运动稳性的影响规律,开展了风浪流工况时域分析。

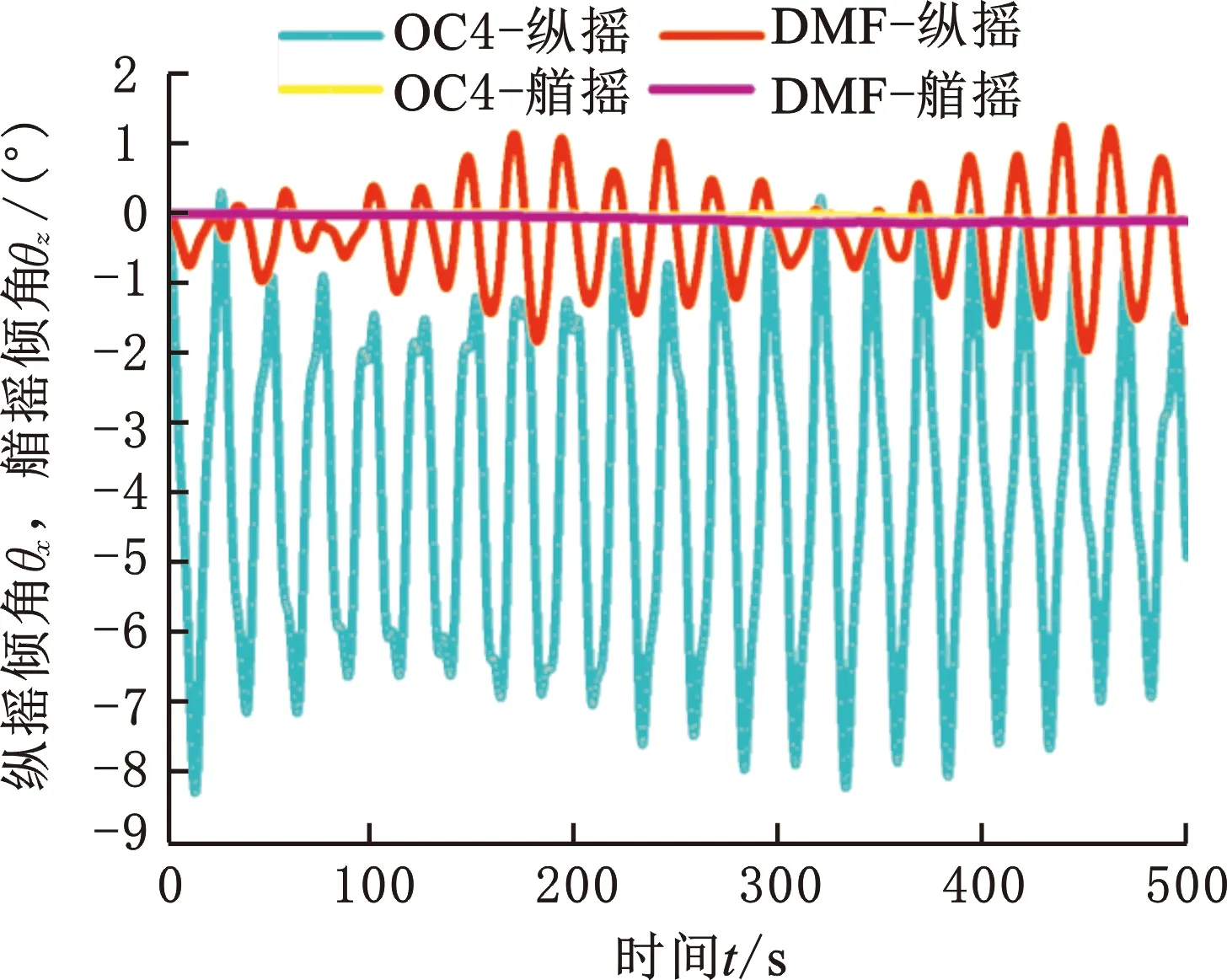
在风浪流载荷下开展DMF运动响应分析是最接近实际海洋工况的模拟,本研究重点关注DMF对复杂海洋环境的适应性。设置风参数:单风机平均气动载荷为800 kN[10],作用点在风机塔筒上,作用高度为水线面基准面以上100 m。设置浪参数:波高为5.49 m,周期为11.3 s,采用规则波输入方式,设定波流流速为0.39 m/s,流域范围为全部水深。采用均匀流速输入方式,方向为x轴正方向,时间步为0.2 s,时长为500 s。DMF和OC4时域仿真分析结果如图6所示。

(a)摇摆时域分析结果

由图6a可得,常规作业工况风浪流作用下,DMF和OC4纵摇响应幅值均呈周期性波动。其中DMF纵摇幅值为±2°,OC4纵摇幅值为0.5°～8.5°。由图6b和图6c得出,DMF的横荡响应幅值与系泊张紧力幅值明显高于常规OC4基础平台,主要因为DMF承载6台风电机组的水平风力,为OC4的6倍,基于力学平衡定理,系泊张力也约为OC4张力的6倍。

5 实验模型与测试

本研究进一步开展了新型点阵式风机系统模型样机加工和波流水槽模拟实验,通过自有衰减测试和风浪流水动力测试来验证DMF水动力响应规律。为了保证试验数据能够反映真实的情况,模型应与实物的物理性质尽可能接近,以水动力主导的水池模型样机实验,实验模型加工尽可能满足Froude和Reynolds相似。按照缩尺比1∶200进行实验模型的加工制作。

模型样机加工严格按照物理参数相似比数据,在保证模型结构密封性的前提下充分考虑结构安全强度问题。模型主体框架材料选用玻璃钢,可满足结构尺寸和浮力平衡要求。风机和网衣采用聚乙烯材料,整体结构质量通过砝码块配重调整,从而调整水线面位置。为对模型的干重以及重心位置严格控制,先在水池中平衡再进行实验。DMF一体化装置模型如图7所示。

(a)水槽 (b)实验模型 (c)检测器

模型实验研究在中国石油大学(华东)水动力实验室拖曳水池中开展。额定作业工况的参数设置为:波高5.49 m,周期11.3 s,风速11.4 m/s,流速0.39 m/s。按照相似原则转换得:波高0.027 m,周期0.806 s,风速0.81 m/s和流速0.028 m/s。风浪流载荷施加方向均为x轴正方向,得到水动力响应结果如图8和图9所示。

图8 纵摇时域分析结果

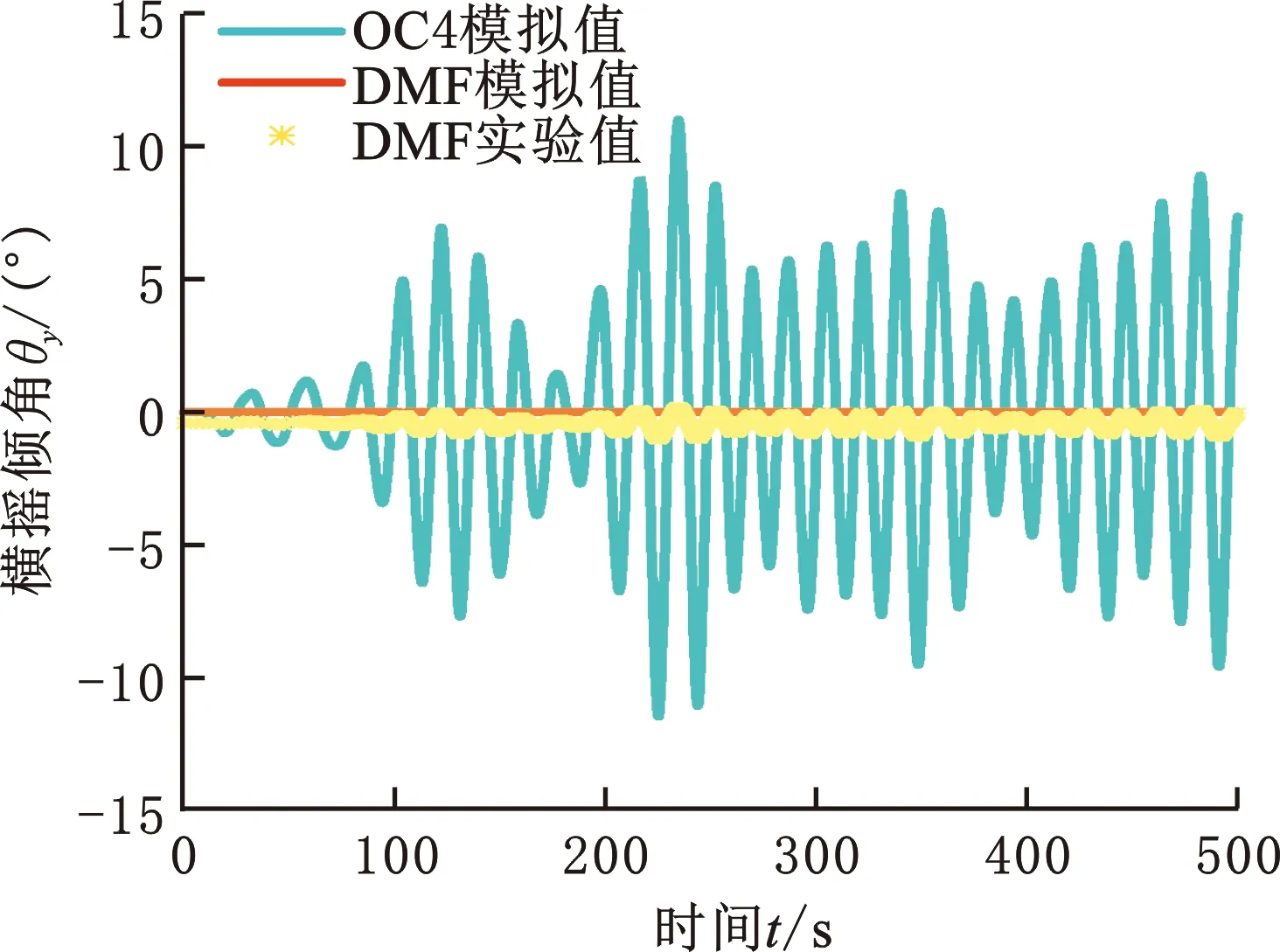
图9 横摇时域分析结果

由于风浪流作用下的运动耦合状态较为复杂,额定作业工况下,水动力运行响应中的摇摆角响应是衡量海上浮式风机发电的关键,因此重点对纵摇和艏摇响应参数进行测试分析。DMF的纵摇响应幅值为2°,OC4的纵摇响应幅值为9°,稳性提高超过70%;DMF的艏摇响应幅值为0.5°,OC4的艏摇响应幅值为10°,稳性提高超过90%,论证了点阵式风电机组一体化基础结构的优越性。

6 结论

(1)基于点阵式风电机组一体化基础(DMF)结构的特殊性,建立了考虑水线面和惯性矩的力学模型。相较于传统风倾力矩稳性方程根据浮心变化规律确定初稳性的方式,DMF稳性平衡方程能更直观地确立浮式结构参数与纵摇初稳性的关系,提供了便于理论模型与数值模拟的水动力稳性作对比的方法,为新型浮式结构概念设计阶段稳性规律研究提供了参考。

(2)考虑风浪流多因素环境作用,开展了DMF气动-水动力模拟仿真和实验测试研究。结果显示DMF的纵摇运动稳性较传统OC4具有较大的优越性,在不同环境载荷作用下,DMF的纵摇运动稳性较传统OC4均提高约70%。该结论同样论证了本研究中基于水线面和惯性矩的初稳性力学模型的准确性和可行性。

(3)为进一步验证DMF建立模型准确性和结构自身固有频率等开展了新型点阵式风机系统模型样机加工和波流水槽模拟实验,通过自有衰减测试和风浪流水动力测试,结果表明数据与仿真结果吻合度较高,由于模拟中未考虑水的黏性阻尼和涡流效应,因此响应幅值数据略大于实验结果,误差小于5%,不影响结果准确性验证。

在风电渔业系统中的可行性研究仍有许多挑战,下一步研究考虑:6台风电机组布置方案优化、长期疲劳的影响、海浪撞击效应、极端海况下的有效生存策略以及新组合系统的优化设计。