基于BAS和Q-Learning的移动机器人路径规划算法研究

程晶晶,周明龙,邓雄峰

(1.安徽机电职业技术学院,安徽 芜湖 241000; 2．安徽工程大学,安徽 芜湖 241000)

0 引言

伴随着移动机器人技术的快速发展,移动机器人在交通导航、移动场库、特种作业等领域得到了广泛的应用。路径规划是移动机器人开发的核心技术,其目的是在复杂的环境中规划出最短、最优的无碰撞路径。目前被广泛应用的路径规划算法有A*算法[1]、快速搜索随机数(Rapidly-Exploring Random Tree,RRT)[2]、人工势场法[3]和蚁群算法[4]等,但这些算法在完全未知的环境下往往不能够达到预期的路径规划效果。强化学习算法具有比较强的适应性,能够在完全未知的环境下通过不断试错的方式规划出最优路径,在移动机器人路径规划中被广泛地应用[5]。Q-Learning是被普遍应用的强化学习算法,同时在人类无法到达或者比较危险的未知环境下能够进行移动机器人路径规划的能力引起了学术界的关注。JIANG等[6]联合神经网络和Q-Learning算法解决了移动机器人在不同环境下的路径规划问题,使得算法的收敛性能大大提升。PENG等[7]采用栅格法构建了移动机器人运动地图环境,并对Q-Learning进行改进,使移动机器人能够在静态复杂的障碍物环境下快速到达终点。大量的实践表明,传统Q-Learning存在起始阶段盲目搜索、动作选择策略不科学的问题[8]。基于此,本文提出了联合天牛须搜索(Beetle Antennae Search,BAS)和Q-Learning的移动机器人路径规划算法,并将其应用于仿真和实物试验中,验证所提出算法的有效性。

1 理论基础

1.1 Q-Learning算法

强化学习是从环境状态到动作映射的学习,算法学习依赖于个体在环境中所得到的反馈信号。Q-Learning是离线时序差分强化学习算法,Q表为机器人自主学习所得到的反馈,即机器人和环境交互感知后的结果,对Q表的更新过程就是机器人和未知环境交互的过程。不妨设移动机器人的当前状态为s(t),a为当前状态所选择的动作,在未知环境作用下产生新的状态s(t+1),回报为r(s,a),Q表更新公式为[9]

(1)

式中:(s,a)为当前状态-动作对;(s′,a′)为下一时刻状态-动作对;α为学习率,取值大于1;γ为折扣因子,取值为0～1。

Q-Learning学习过程中采用ε-贪婪策略选择下一个状态的动作,即移动机器人以ε概率随机在动作空间选择动作,以1-ε概率选择最优动作。

1.2 天牛须搜索

BAS是根据天牛觅食过程中所提出的智能优化算法,其假设天牛左右触角在天牛质心左右两边,觅食步长与触角距离之比为定值,天牛每走一步其头朝向随机,其具体步骤[10]:

第1步:初始化

初始化左须坐标为xl,右须坐标为xr,质心坐标为x,左右须距离为d0,步长为step。

第2步:归一化

产生随机向量表示右须指向左须朝向,并对朝向归一化

(2)

那么天牛左右须位置可以表示为

(3)

第3步:构造迭代格式

设f为待优化函数,定义Fl=f(xl),Fr=f(xr),迭代格式为

(4)

第4步:迭代终止条件

设置迭代终止条件,如寻优精度、最大迭代次数,如果满足迭代终止条件,则迭代结束,输出最优结果;如果不满足迭代终止条件,则继续迭代。

2 联合BAS和Q-Learning的路径规划算法

2.1 Q表初始化

传统Q-Learning将所有Q值初始化为0或者随机数,这会造成大量无效迭代。在初始化阶段引入环境先验知识,采用任意位置栅格到目标点栅格欧式距离来定位D(xi,xg),到起始点栅格欧式距离来定位D(xi,xx),设

D(xi)=(1-η)·D(xi,xg)+η·D(xi,xx),

(5)

式中η为权重系数,取值为0～0.2。

采用D(xi)的线性归一化数值来对Q表初始化,这样避免了大量无效迭代,使得下一路径点选择更具目的性,提高了算法收敛速度。

2.2 动作选择策略

传统Q-Learning搜索决策分为直接搜索和间接搜索,即有先验知识采用直接搜索,否则采用间接搜索。对传统Q-Learning算法搜索时间和学习速度进行平衡改进,即移动机器人以概率ε进行探索,以概率1-ε放弃探索,执行最高价值动作,动作选择策略公式为

(6)

该动作选择策略依据探索步长栅格的有效状态来动态调整搜索概率,避免搜索陷入局部最优。另外,在对步长探索阶段寻优基础上增加环境回报,从而动态调整搜索因子,即

(7)

式中λ为衰减系数,N为步长总数量,Δx为阶段补偿探索有效回报状态。

2.3 BAS优化Q值

根据马尔科夫决策给定状态集S和行为集A,其中s∈S,a∈A,Q(s,a)为s状态下选择行为a的分数。根据Q值可以知道状态s时的行为选择,选择使得Q值最大的动作为a。不妨设定s1、s2、s3、s4为4个状态,前3个状态的动作为a1、a2、a3,第4个状态没有动作。r1、r2、r3为si状态时执行ai动作的奖励(i=1,2,3),设γ∈(0,1)为衰减因子,那么

(8)

通过归纳法可以得到:

Q(si,ai)=ri+γQ(si+1,ai+1)。

(9)

由于s包含多个动作选项,这需要利用状态最大行动的Q值,即

Q(si,ai)=Q(si,ai)+a(ri+γmaxQ(si+1,A)-Q(si,ai))。

(10)

为了避免陷入局部最优状态,采用BAS进行优化处理。传统Q-Learning搜索的范围有限且仅仅探索下一步的动作,通过BAS的融入使移动机器人在路径规划时可以深度探索,获取在规划路径上的动态障碍物位置信息,避免陷入局部最优的状态。

考虑到规划路径存在比较多的转折点,采用贝塞尔曲线进行平滑处理,使所规划的路径更加平顺。贝塞尔曲线差值表达式为

(11)

式中t为变量,bi为曲线上的第i个控制点,Bin(t)为贝塞尔基函数。

3 仿真分析

3.1 静态障碍物仿真

选择20×20的栅格地图模型,圆圈表示移动机器人的初始位置,五角星表示移动机器人的目标位置,黑色区域为障碍物,具体如图1所示。

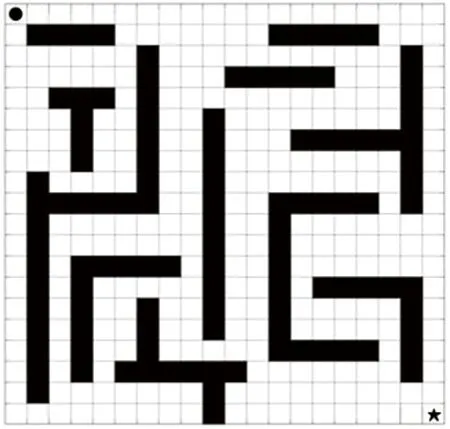
图1 构建的栅格地图模型

分别采用传统Q-Learning和BAS-Q-Learning进行路径规划,路径规划结果如图2所示,迭代次数和规划路径长度关系如图3所示。

图2 静态障碍物路径规划结果

由图2可知,相对于传统Q-Learning算法,BAS-Q-Learning算法规划得到的路径转折点比较少,路径也更为平顺,能够有效满足移动机器人的动力学约束,在实际的工程中具有更好的适用性。由图3可知,尽管对Q-Learning算法改进前后得到的最优路径长度是相等的,但是BAS-Q-Learning的迭代次数明显减少,即迭代收敛的效率大大提升。

图3 静态障碍物迭代次数与规划路径长度关系曲线

3.2 动态障碍物仿真

移动机器人的服役环境常常存在动态障碍物,BAS-Q-Learning算法能够有效地在动态障碍物环境下对移动机器人进行路径规划。采用算法在20×20的栅格地图模型上生成随机动态障碍物,使得栅格地图上不仅有静态障碍物,同时还有动态障碍物。图4为动态障碍物环境下的分段路径。

图4 动态障碍物环境下的分段路径

由图4可知,BAS-Q-Learning路径规划算法能够及时避开随机障碍物,在各阶段规划出最优的局部路径。图5为动态障碍物环境下的路径规划结果,规划路径和黑色障碍物重叠的部分是动态障碍物导致的,移动机器人在经过时,该区域是没有障碍物的,即不会产生移动机器人和动态障碍物发生碰撞的情况。

4 实物试验分析

在所搭建的实物试验环境中不仅包含有固定的障碍物,同时也有随机出现的动态障碍物,所搭建的静态障碍物环境如图6所示。图中的4个立方体为静态障碍物,5个长方体为墙壁,SP位置为移动机器人的起始位置,EP位置为移动机器人的目标位置,需要规划一条从SP到EP的最优路径。在实际的试验过程中,加入动态障碍物对路线进行干扰,验证算法在动态障碍物环境下的路径规划性能。试验所用移动机器人的尺寸为500 mm×300 mm×160 mm,每一个正方形地砖为1个栅格,其边长为500 mm。

图5 动态障碍物环境下的路径规划结果

图6 搭建的试验环境

在实际试验的过程中采用传统Q-Learning出现了2次碰撞,这主要是由于所规划的路径存在比较多的急转弯,而移动机器人因自身的惯性导致其无法及时躲避动态障碍物。采用BAS-Q-Learning算法在实际试验的过程中未发生碰撞。表1为对比结果,可知采用BAS-Q-Learning算法所规划的路径长度明显缩短,缩短长度为623.94mm,缩短比例为25.9%;重新规划用时减少了6.11 s,减少比例为88.7%;整体用时减少了19.09 s,减少比例为63.1%;另外,拐点数目也由8个减少到2个。图7为路径规划过程。

表1 实物试验结果对比

图7 移动机器人路径规划过程

5 结论

对Q-Learning路径规划存在的起始阶段盲目搜索、动作选择策略不科学的问题,采用欧式距离定位坐标,更新了动作选择策略,并融入BAS,实现移动机器人路径规划。采用贝塞尔曲线对规划的路径进行平滑处理,使其具有更强的工程适应性。将提出的BAS-Q-Learning应用于仿真试验和实物试验中,结果表明,该算法的迭代效率大大提升,能够及时有效地避开随机动态障碍物,这对移动机器人更加准确、高效地实施路径规划提供了参考。