基于非线性和神经网络的小型四旋翼飞行器机器人控制

谭 超,朱荣钊

(1.厦门华天涉外职业技术学院 信息技术学院,福建 厦门 361102;2.湖北大学 计算机与信息工程学院,武汉430062)

0 引言

无人机器人因其具有广泛的应用前景而越来越受到人们的关注[1]。虽然无人机市场最初是由军事应用和大型昂贵的无人机驱动的,但最近小型化、机电一体化和微电子技术方面的研究成果也为小型和廉价的商用无人机提供了巨大的发展潜力[2]。这些小型无人机能够在室内或室外飞行,从而带来了全新的应用前景。

四旋翼是一种很有前途的飞行器,它由4个螺旋桨组成。前后马达在顺时针方向转动时,左右马达均会逆时针方向转动,可有效地消除回旋作用及调节飞机的空气动力扭矩[3]。四旋翼相对于常规直升飞机来说,其优势在于它可以简化旋翼的动力学。除此独特的机械构造之外,四旋翼还内置了各种感应器及资讯处理装置,使无人机能够自行操纵[4-6]。

虽然四旋翼具有4个操纵器,但它仍然是一种不稳定的动力学系统,它需要一个适当的控制系统来保持其平稳。由于系统的动力学特性是非线性的,因而使得控制算法更加复杂。该方法不仅具有复杂的功能,而且还需要在嵌入式系统中进行,同时还要兼顾内存和高性能的芯片处理能力。在四旋翼飞机的控制系统中,有很多都是以线性模型为基础的,而其他方法则采用滑模控制或H∞控制。在航空航天应用中的一些控制技术,还没有应用于小型四旋翼无人机的控制[7-9]。以此为出发点,本文对相关算法进行了进一步的改进,并通过适当的神经网络的加入进行了扩展。初步的仿真结果显示本文改进后的算法具备可行性。

1 四旋翼无人机系统

1.1 结构特点

四旋翼无人机的移动是由4个转子的升力来实现的,它可以通过改变转速、迎角(俯仰角)、旋转俯仰角等方式改变升力矢量。由于转子是采用弹性塑料制造的,螺距角度是固定的,气动扭转会引起螺距角度的改变,所以四转子的升力是4个转子的速度之和,扭矩是两者之间的关系。

4种输入动力的四旋翼无人驾驶飞机可实现6个自由度的移动[10-11]。通过驱动的组合,它可以控制6个自由度的运动,尽管不可能实现非耦合运动,但结合精细和不断变化的几个驱动器,一个非常熟练的操作人员可以使四旋翼无人机悬停。

1.2 特点分析

为有效解决四旋翼飞行器机器人的动态不稳定性问题,常常通过调节系统参数的方式增强稳定性[10]。在四旋翼飞行器机器人上增加4个反向的旋转转子,这样机器人在大风环境下飞行时反向旋转转子就会产生推力确保飞行器的动态稳定性。另外,增加反向旋转转子后飞行器的尺寸和重量变大,这也在一定程度上确保了飞行器飞行时的稳定性。由于四旋翼无人机具有故障诊断和容错功能,这使得飞行器旋翼部位出现损坏时其依旧能够稳定飞行。因为当飞行器的部分转子出现故障时,飞行器机器人的控制系统能够快速对故障实施诊断并进行容错飞行控制,无故障的转子补偿有故障转子的功能,就确保了无人机飞行的稳定性。

1.3 系统设计

四旋翼飞行器机器人飞行时的推力系数与阻力系数由螺旋桨试验特征进行估算获得,结合经验设计推力与重力比为1∶8,并通过迭代来估计飞行器机器人机体与航空电子的质量。图1为四旋翼飞行器机器人。

图1 四旋翼飞行器机器人

四旋翼飞行器机器人旋转动力学具有反馈机制,可以采用反演来设计机器人的姿态控制器。由于虚拟控制变量解析导数形式十分复杂,对不稳定系统更是如此,这使采用反演方法设计的机器人姿态控制器的使用受到很大限制。实际的姿态控制系统采用的是直接提取角速度差分信号,从而极大地减少了对系统的依赖。提高飞行器机器人姿态控制器的鲁棒性,使扰动重构误差对四旋翼飞行器机器人的跟踪能力增强。

2 四旋翼的动力学模型

四旋翼的姿态由3个欧拉角给出,即偏航角ψ、俯仰角θ和侧倾角φ,它们共同形成矢量ΩT=(φ,θ,ψ)。惯性系中四旋翼的位置由矢量rT=(x,y,z)给出。从固定帧到惯性帧的矢量的变换由旋转矩阵R给出,其中cθ表示cosθ,sθ表示sinθ:

(1)

由于转子i产生的推力是Fi=b·ωi2,i=1,2,3,4,b是推力因子,ωi是转子i的速度,从而得到第1组微分方程,描述了四旋翼加速:

(2)

利用惯性矩阵I(主对角线上具有惯性Ix、Iy和Iz的对角矩阵),转子惯性JR和描述施加到机身的扭矩的矢量τ,可得到第2组微分方程:

(3)

矢量τ定义为

(4)

使用阻力系数d和杠杆的长度l。转子的4个旋转速度ωi是实际四旋翼的输入变量。因此,获得新的输入变量:

(5)

在之前的公式中得到的另一个变量也取决于转子的转速,因此必须考虑第5个人工输入:

u5=ωd=ω2+ω4-ω1-ω3。

(6)

因此,将前述公式合并后可得整体动态模型:

(7)

(8)

由式(7)和式(8)可得到:

(9)

式中I1=(Iy-Iz)/Ix,I2=(Iz-Ix)/Iy,I3=(Ix-Iy)/Iz。

因而此时状态空间模型可以分解为描述姿态动态(角度)的一个微分方程子集和一个描述无人机平移的子集。由式(9)可得到第1个微分方程子集,称为子模型M1:

(10)

该子模型的人工输入变量为变量u2、u3、u4和u5。根据M1输出的角速率,通过数学积分可获得角度。而所获得的3个角度(状态变量x7、x9和x11)是下一个子模型M2的输入。

3 机器人控制器

从控制工程的角度讲,无人机系统包含两个主控制回路:第一个主控制回路和底层控制回路。第一控制回路负责无人机当前所需运动的产生和稳定。底层主回路是任务控制回路,包括稳定四旋翼的设备、与任务相关的传感器和执行机构以及任务控制系统的平台。任务控制回路计算所需的飞行路径,由GPS航路点给出,向四旋翼控制回路发出当前所需的运动指令。

在这个方法中,假定任务控制系统向四旋翼控制系统输入一个速度矢量。然后必须建立和稳定所需速度矢量。为了获得速度控制所需的测量值,四旋翼控制回路必须配备合适的惯性测量系统。该测量系统提供了加速度和角速度,用来进一步计算速度和欧拉角。本文的研究重点为四旋翼控制回路(无人机所需速度矢量的控制),并在此基础上设计了四轴驱动的嵌套结构。要实现并维持理想的速度向量,就需要对飞行器的姿态进行稳定。为此,本文对内环和外回路的转速进行了分解。在这种结构下,内部的姿态控制电路必须远高于外部环路,并且能够使外部环路所控制的角度保持稳定。这个嵌套的构造如图2所示。

图2 无人机四旋翼控制的嵌套结构

考虑内部控制回路、控制器C1和姿态控制回路,必须稳定所需的滚动角、俯仰角和偏航角,即所需的向量ΩTd=(φd,θd,ψd)=(x7,d,x9,d,x11,d)。相应的动态模型包括状态空间模型式(8)的最后6个方程,是一系列非线性子模型M1和积分器。再以此为基础导出外环控制器C2,以稳定所需的速度矢量。

3.1 Riccati状态控制方程

基于状态的Riccati方程(SDRE)控制最初由Cloutier推导得来。其基本思想是由线性二次调节驱动,并引入非线性系统分解,使其在任何固定状态下变为线性驱动:

(11)

矩阵A和B都取决于当前的状态变量。针对这些方程的可控性问题,可使用标准线性最优控制理论计算任何状态x的控制增益,即选择最小化成本函数控制:

(12)

式中Q(x)为惩罚状态,R(x)为惩罚控制。从而进一步求解代数Riccati微分方程,可得:

ATP+PA+Q-PBR-1BTP=0。

(13)

由式(13)得到矩阵P(x),此时控制增益变为

u=-K(x)x=-R(x)-1BT(x)P(x)x。

(14)

通常,该方法要求在每个状态下求解代数Riccati方程,因此还必须在每个状态下重新计算控制增益。

3.2 使用SDRE进行姿态控制

(15)

该因式分解并不是唯一的,在式(15)中,矩阵A(xI)和B(xI)都是状态相关的,即式(15)可以写作:

(16)

使用式(16)可计算控制增益矩阵K(xI),而总控制输入uI须考虑由外部速度控制环给出的期望状态xI,d是稳定的。假设已经确定了控制增益矩阵K(xI),则可通过预滤波器矩阵M(xI)保证非零期望状态的稳定:

M(xI)=pinv((B(xI)K(xI)-A(xI))-1B(xI)),

(17)

式中pinv()表示非二次矩阵的伪逆。此时,整体姿态控制律即控制器C1可以概括为

uI=-K(xI)xI+M(xI)xI,d。

(18)

4 非线性和神经网络控制

4.1 使用神经网络进行速度控制

若内环姿态控制足够快,可假设滚动、俯仰和偏航的期望值与外部速度控制环相比,角度实现得非常快。因此,闭合的内部控制回路可近似被认为是静态块,那么仅需将滚动、俯仰和偏转角的期望值传递到下一个模型M2。此时可通过一组非线性微分方程描述模型M2:

(19)

式中x7d、x9d、x11d和u1都是输入变量。式(19)可用所有微分方程都具有的形式来解释:

(20)

(21)

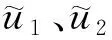
(22)

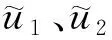
(23)

因为矢量函数f太过复杂,所以不能用封闭的形式得到反函数。所以,利用神经网络进行逆解。再来考虑1个简单的神经网络训练:要达到任意所需的速度向量,不必应用偏航旋转,因此可设置x11d=ψd=0。

其次,对神经网络的类型、内部结构和学习算法进行了研究。本文将多层次感测器应用于前向神经网络中。在输入层有20个神经元,在隐藏层中有20个,在输出层有4个,在输出层有4个。试验结果表明:1 000个以上的输入和输出数据可以满足对所选神经网络的要求。图3是第一个100个数据点的输入变量,以及每个输入变量的数值都是由神经网络计算出来的。

图3 训练的神经网络示例结果

4.2 使用神经网络计算实际输入变量

内部姿态控制器C1和外部速度控制器C2共同产生人工控制矢量uT=(u1,u2,u3,u4,u5)。因为实际输入变量为4个转子i=1,…,4的转速ωi,这些输入变量不能应用于真正的四旋翼无人机中。因此,需使用式(5)～(6)计算这4个变量。同样,本文通过1组5个非线性方程求解计算4个未知数(ωi的值)。由于没有封闭形式的解决方案,因而本文再次应用神经网络来执行此计算。

如前所述,首先使用式(5)中旋转速度ωi的随机值和相应的uT=(u1,u2,u3,u4,u5)的计算值创建1组合适的训练数据。再次,将这些uT计算值的数据集作为输入变量,而相应的ωi(i=1,…,4)值为学习的输出变量。其次,使用Matlab神经网络工具箱中反向传播算法选择多层感知器。神经网络由输入中的20个神经元,隐藏的20个神经元和输出层中的4个神经元构成。本文使用4 000个数据集进行训练,以获得足够准确的计算结果。在控制系统中实现所得到的神经网络,将人工输入变量uT=(u1,u2,u3,u4,u5)变换为实际输入变量ωi(i=1,…,4)。此时整个四旋翼控制结构如图4中所示。图5和图6分别为四旋翼飞行器机器人俯仰角跟踪响应调节参数和确定参数。

图4 四旋翼整体控制结构

图5 四旋翼飞行器俯仰角跟踪响应调节参数

图6 四旋翼飞行器俯仰角跟踪响应确定参数

5 结论

四旋翼飞行器提供了在室内或室外飞行的可能性。但由于这些四旋翼的非线性动态特性,其稳定控制和制导是一项艰巨的任务。以此为出发点,介绍了一种新型四旋翼微型无人飞行器的综合控制方案,包括状态相关的Riccati方程(SDRE)控制以及神经网络。该算法的动态模型是基于Matlab/Simulink模拟模型进行推导与实现的。对非线性四旋翼控制系统仿真测试结果显示了此控制方法在当前现实中的可行性。