三维堆叠封装TSV 互连结构热扭耦合应力分析与优化

谢俊 ,黄春跃 ,梁 颖 ,张怀权 ,刘首甫

(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;2.成都航空职业技术学院 信息工程学院,四川成都 610021;3.模式识别与智能信息处理四川省高校重点实验室,四川 成都 610106)

集成电路(IC)封装器件不断朝小型化、多功能化、高性能化和高集成化方向发展。为了更好地满足这些需求,三维集成电路技术应运而生且被广泛使用。而硅通孔(Through-Silicon-Via,TSV)互连技术作为实现三维集成电路的关键技术[1],其衍生出的TSV 互连结构在三维集成电路中承担电互联、信号传递及机械支撑等作用,其结构的可靠性将直接或间接影响整个三维集成电路的可靠性。TSV 互连技术被广泛应用于车载、机载和移动设备上[2],从而导致应用TSV 互连技术的IC 器件在工作过程中将不可避免地出现因受外力而变形的情况。其中热变形和扭转变形是最为常见的两种变形,如因工作环境温度的周期性变化,会导致TSV 互连结构产生热变形而承受热应力,在集成电路组装和使用过程中不同程度地产生扭转变形而承受一定的弯扭应力。这些变形会造成三维集成电路中的TSV 互连结构产生裂纹和变形等损伤,进而影响TSV 互连结构的可靠性,给基于三维集成电路的IC 器件可靠性带来了更为严峻的挑战。

针对TSV 互连结构可靠性的问题,国内外学者已经展开了相关研究工作,Chen 等[3]分析了热循环试验下硅通孔(TSV)转接板的可靠性,在1000 次热循环后,沿顶部界面会产生裂纹和TSV 铜柱变形;Okoro等[4]研究了热循环条件下硅通孔(TSV)的可靠性,TSV 互连结构的电阻会随着热循环次数的增多而增大;Wang 等[5]建立了具有内部微通道和全铜互连的三维集成电路器件的有限元模型,研究了热循环载荷下TSV 结构的热力学性能;Lee 等[6]提出了一种双层薄叠片封装方法,研究了温度循环载荷下封装翘曲对SnAg 微焊点疲劳寿命的影响;黄春跃等[7]研究了在热-结构耦合条件下硅通孔互连结构参数对应力应变的影响规律;丁英涛等[8]对BCB 介质层同轴TSV 的热力学特性进行了研究分析;邓小英等[9]利用有限元仿真方法对低阻硅TSV 以及铜填充TSV 的热力学性能进行了对比分析,相比于铜填充TSV,低阻硅TSV 具有更高的热力学可靠性。以上学者的研究工作一方面表明热应力对TSV 互连结构可靠性的影响显著,另一方面也表明已有的研究工作尚有不足,如大多只是分析了TSV 的热力学性能,尚未考虑到扭转变形等载荷,也未见到同时在热循环与扭转复合加载条件下的TSV 互连结构可靠性研究报道,针对TSV 互连结构在热扭复合加载条件下的结构参数优化设计的研究也较少。

鉴于此,本文以三维集成电路中的TSV 互连结构为研究对象,对其在热循环与扭转耦合加载条件下的应力应变进行分析,研究TSV 互连结构参数与材料参数对其应力的影响规律。在此基础上运用响应面与模拟退火算法相结合的优化方法对TSV 互连结构在热扭耦合加载下进行结构参数优化设计,达到降低TSV 互连结构应力和优化TSV 互连结构参数的目标,从而提高TSV 互连结构的可靠性。

1 TSV 互连结构在热扭耦合加载条件下的有限元分析

1.1 TSV 互连结构的有限元分析模型设计

本文以三维TSV 芯片垂直堆叠封装结构中的TSV互连结构为研究对象,建立简化后的三维TSV 芯片垂直堆叠封装结构有限元模型(下文简称有限元模型)如图1 所示。有限元模型的几何模型包括叠层芯片、TSV 铜柱、绝缘层、填充层、微凸点、基板、焊点和印制电路板(PCB)八部分,其中焊点与微凸点材料均为SAC305,焊点为5×5 阵列,绝缘层材料为SiO2。模型中各部分的尺寸参数: PCB 为33 mm×19 mm×1 mm,焊球直径和高度分别为350 和280 μm,间距为600 μm,基板为3.5 mm×3.5 mm×625 μm,填充层为2.8 mm×2.8 mm×20 μm,TSV 铜柱的直径与高度分别为40 和75 μm,微凸点的直径与高度分别为60 和20 μm,芯片为2.8 mm×2.8 mm×75 μm,绝缘层的厚度为3 μm。

图1 三维TSV 芯片垂直堆叠封装结构有限元模型Fig.1 Finite element model of 3D TSV chip vertically stacked package structure

有限元模型中焊点与微凸点单元类型选用Visco107 粘塑性实体单元,其他结构全部采用Solid185 实体单元,有限元分析模型使用的材料参数如表1 所示。表中展示了FR-4、SAC305、硅、填充层、铜和SiO2等材料的热膨胀系数、弹性模量、泊松比和导热系数等材料性能参数值。

表1 材料参数[10-11]Tab.1 Material parameters[10-11]

对TSV 互连结构进行热循环加载时,选用美国军用标准MIL-STD-883 热循环加载条件[12],升降温速率均为36 ℃/min,最大温度为125 ℃,最小温度为-55 ℃,温度差为180 ℃,分别在高温和低温时保温10 min,经历一个周期的时间为1800 s,零时刻参考温度为125 ℃。对PCB 底面四个顶点的自由度进行全约束,并施加热循环载荷曲线,如图2 所示。该曲线中共有四个热循环过程,以第四个循环周期为例,图中的a、b、c、d、e 分别对应时间为5400,5700,6300,6900 和7200 s,其中b、c、d、e 四个点在本文中分别称为低温保温开始时刻、低温保温结束时刻、高温保温开始时刻和高温保温结束时刻。

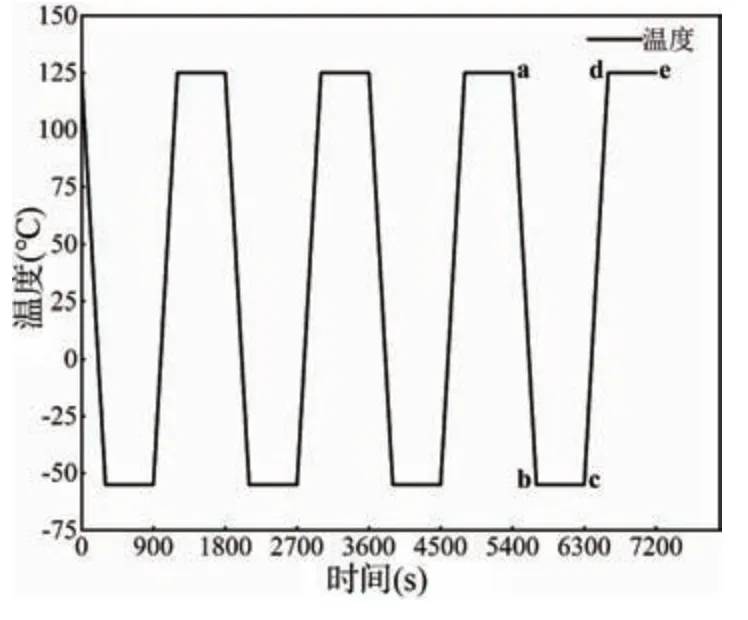
图2 热循环加载曲线Fig.2 Thermal cycle loading curve

图3 所示为三维TSV 芯片垂直堆叠封装结构有限元模型进行扭转加载的示意图。选择PCB 板的四个顶点,对其施加大小相等而方向不同的位移载荷F(如图3 所示),使得整体模型产生扭转载荷,继而导致TSV互连结构内产生扭转应力应变。

图3 施加扭转载荷示意图Fig.3 Schematic diagram of applying torsional load

1.2 TSV 互连结构的热扭耦合应力应变分析

对三维TSV 芯片垂直堆叠封装模型施加热循环与扭转载荷时,运用间接耦合法进行求解。耦合过程先进行热循环分析,得到TSV 互连结构在热循环加载条件下的结构应力分布情况。再以热循环加载条件下的热结构应力作为预应力,施加到扭转载荷加载条件下的结构场中,进行有限元分析,求解得到不同时间下的TSV 互连结构最大热扭耦合应力应变,如图4 所示。由图4 可知,TSV 互连结构的热扭耦合应力随温度变化而变化,且TSV 互连结构的最大应力在热循环过程中呈增大趋势。第三个循环与第四个循环的最大应力相差不大,表明TSV 互连结构的热扭耦合应力在经历四个循环后逐渐趋于稳定,故本文主要针对第四个循环进行分析。

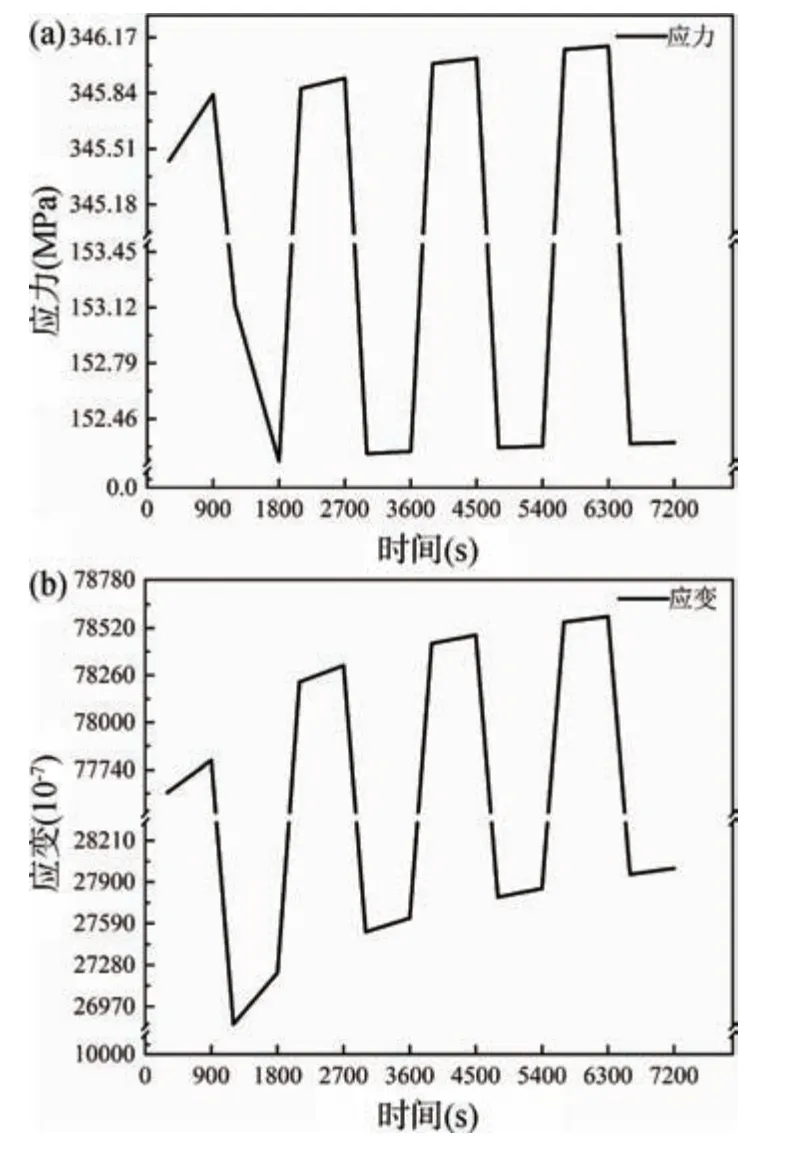
图4 TSV 互连结构应力应变随时间变化图。(a)应力随时间变化图;(b)应变随时间变化图Fig.4 Variation of stress and strain of TSV interconnect structure with time.(a) Stress over time plot;(b) Strain over time plot

在第四个循环中,当温度从125 ℃降温到-55 ℃时,TSV 互连结构的应力应变随之增加,在低温保温阶段,TSV 互连结构的应力应变随时间略有增加,并且达到最大应力应变,即最大应力应变产生在低温保温结束时刻。在温度从-55 ℃升温到125 ℃的过程中,TSV 互连结构的应力应变持续下降,在高温125 ℃保持恒温的时候,TSV 互连结构应力应变随时间略有提升,即在高温保温开始时,应力应变达到最低。因此,TSV 互连结构在整个热扭耦合过程中低温阶段的应力应变比高温阶段大得多,且最大应力应变出现在低温保温结束时刻,最小应力应变出现在高温保温开始时刻。

从图5 所示低温保温结束时刻c 的TSV 应力应变分布图可知,对于整个TSV 互连结构来说,最大应力应变出现在铜柱与微凸点接触面外侧,该接触面为靠近基板一侧,且该最大应力点在铜柱上,最大应变出现的接触面为远离基板一侧,且该最大应变点在微凸点上,最大应力和最大应变分别为345.83 MPa和0.0080891。

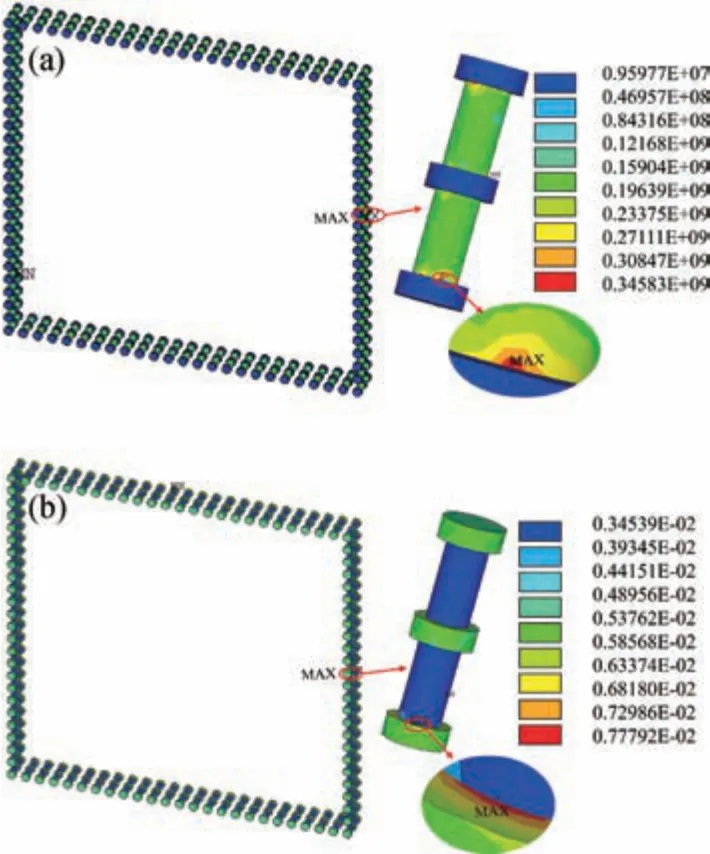
图5 c 点时刻的TSV 互连结构应力应变云图。(a)应力云图;(b)应变云图Fig.5 Stress-strain nephogram of TSV interconnection structure at point c.(a) Stress nephogram;(b) Strain nephogram

2 材料及结构参数对TSV 互连结构的热扭耦合应力影响

2.1 微凸点材料对TSV 互连结构应力的影响

在只改变微凸点材料而其他结构参数不变的前提下,将微凸点材料分别取为SAC305、Pb37Sn63、Pb90Sn10、SAC387 四种材料,建立微凸点热扭耦合加载有限元模型进行仿真分析。得到TSV 互连结构应力应变云图如图6 所示,应力大小如表2 所示。由图6可知,在保证微凸点结构参数不变的条件下改变微凸点材料进行仿真分析,TSV 互连结构的热扭耦合应力会发生改变,但TSV 互连结构最大热扭耦合应力点均出现在铜柱与微凸点的接触面外侧上。由表2 可知,四种微凸点材料对应TSV 互连结构的最大应力应变值相差较大。微凸点为SAC387 材料时,TSV 互连结构最大应力为391.81 MPa。微凸点材料为Pb37Sn63 时,TSV 互连结构最大应力为317.04 MPa。可见不同微凸点材料对TSV 互连结构应力应变有较大的影响,因此对TSV 互连结构相关材料参数进行设计时,需要考虑到微凸点材料的影响。

表2 不同微凸点材料的TSV 互连结构应力Tab.2 TSV interconnect structure stress and strain of different micro-bump materials

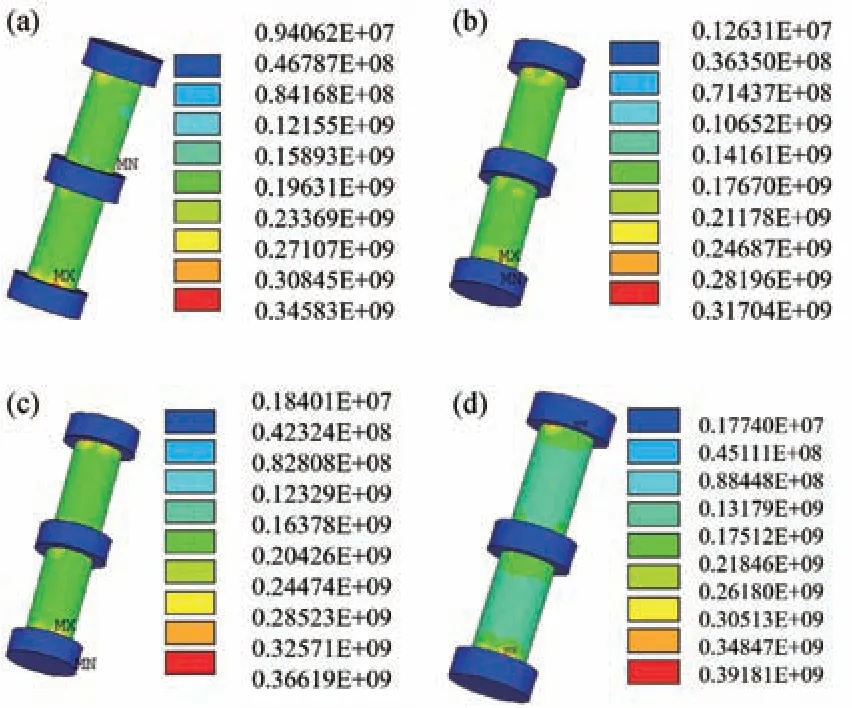
图6 不同微凸点材料下TSV 互连结构应力云图。(a)SAC305;(b) Pb37Sn63;(c) Pb90Sn10;(d) SAC387Fig.6 Stress nephogram of TSV interconnect structure under different micro-bump materials.(a) SAC305;(b) Pb37Sn63;(c) Pb90Sn10;(d) SAC387

2.2 结构参数对TSV 互连结构应力的影响

以1.1 节建立的TSV 互连结构作为基础模型,只改变SiO2层厚度,建立2,3,4 和5 μm 四种SiO2层厚度的有限元模型进行热扭耦合加载下的仿真分析,得到TSV 互连结构最大应力变化如图7(a)所示;只改变TSV 铜柱直径,建立20,30,40 和50 μm 四种铜柱直径的有限元模型进行热扭耦合加载下的仿真分析,得到TSV 互连结构最大应力变化如图7(b)所示;只改变TSV 铜柱高度,建立75,85,95 和105 μm 四种铜柱直径的有限元模型进行热扭耦合加载下的仿真分析,得到TSV 互连结构最大应力变化如图7(c)所示。

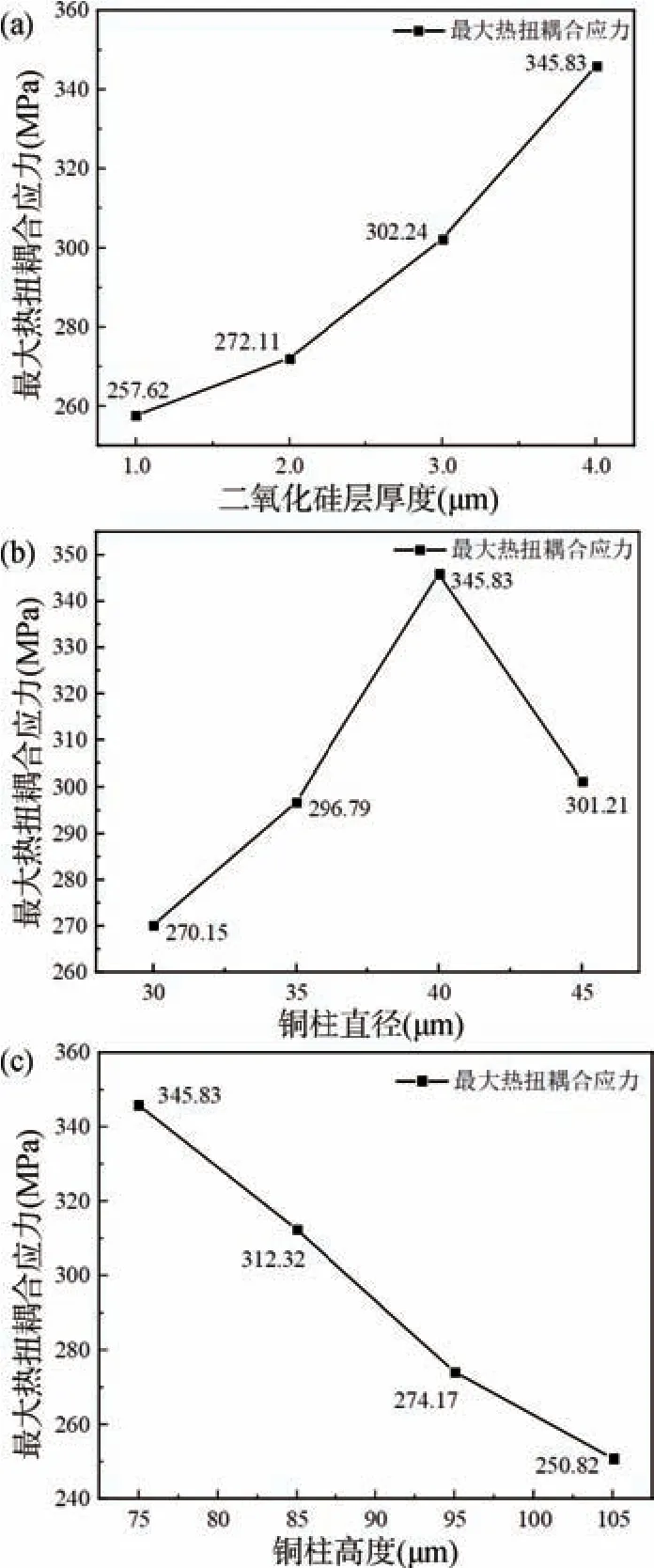
图7 不同参数对TSV 互连结构应力影响变化图。(a) SiO2层厚度;(b)铜柱直径;(c)铜柱高度Fig.7 Effect of different parameters on the stress variation of TSV interconnect structure.(a) SiO2 layer thickness;(b)Copper column diameter;(c) Copper column height

由图7 可知,不同SiO2层厚度的TSV 互连结构在热扭耦合加载下的最大应力应变各不相同,TSV 互连结构最大热扭耦合应力随SiO2层厚度的增大而增大,当SiO2层厚度为4 μm 时,TSV 互连结构应力最大为345.83 MPa;当SiO2层厚度为1 μm 时,其应力最小为257.62 MPa。不同铜柱直径的TSV 互连结构在热扭耦合加载下的最大应力应变各不相同,TSV 互连结构最大热扭耦合应力随铜柱直径的增大而先增大后减小,当铜柱直径为40 μm 时,TSV 互连结构应力最大为345.83 MPa;当铜柱直径为30 μm 时,其应力最小为270.15 MPa。不同铜柱高度的TSV 互连结构在热扭耦合加载下的最大应力应变各不相同,TSV 互连结构最大热扭耦合应力随铜柱高度的增大而减小,当铜柱高度为75 μm 时,TSV 互连结构应力最大为345.83 MPa;当铜柱高度为105 μm 时,其应力最小为250.82MPa。

3 基于响应面与模拟退火算法的TSV 互连结构参数优化

由第2 节可知,结构参数较微凸点材料对TSV 互连结构的热扭耦合应力的影响更大。为了降低TSV 互连结构热扭耦合应力进而提高TSV 互连结构在热扭耦合载荷下的可靠性,本文以降低TSV 应力为目标,基于响应面、模拟退火算法对在热扭耦合加载下的TSV互连结构参数进行优化,得到了优化后的最优参数水平组合,并通过有限元仿真验证了最优参数组合的正确性。

3.1 TSV 互连结构的响应面仿真试验组合设计

试验设计时选用的微凸点材料均使用SAC305,在TSV 几何结构参数中选取SiO2层厚度、铜柱直径和铜柱高度3 个影响因素,将每个因素设定3 个水平值,得到因素水平表如表3 所示。

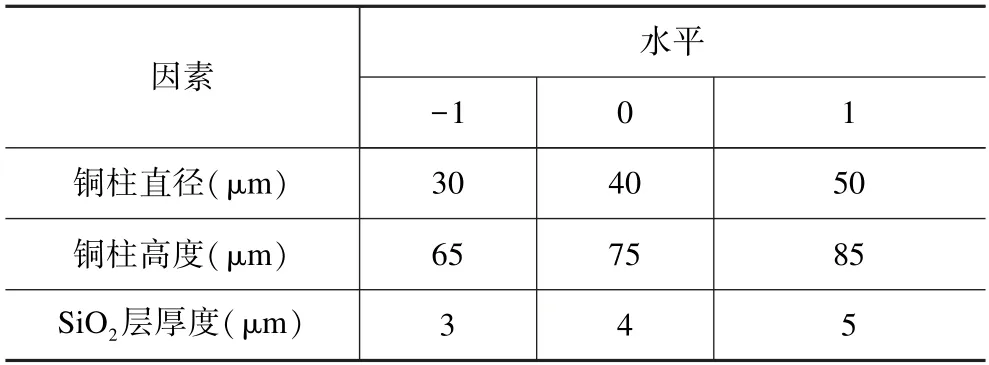
表3 因素水平表Tab.3 Factor level table

选用Box-Behnken 试验设计法得到17 组TSV 互连结构参数水平组合如表4 所示。依据每一组的参数水平组合建立相应的仿真模型进行热扭复合载荷分析,得到TSV 互连结构的最大热扭耦合应力值。

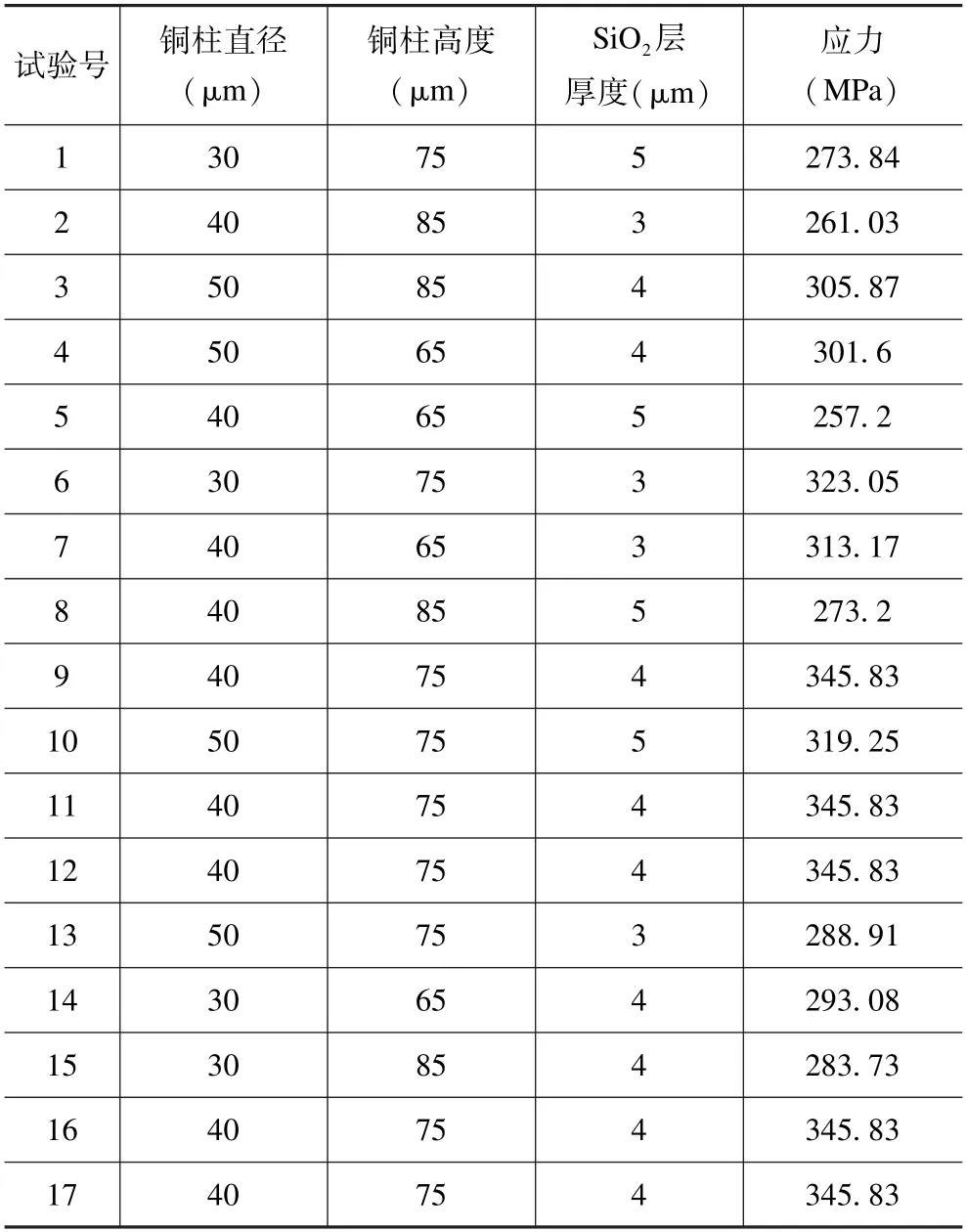
表4 设计组合与热扭耦合应力分析结果Tab.4 Design combination and thermal -torsional coupling stress analysis results

3.2 TSV 互连结构响应面分析

将表4 中每个水平组合的最大热扭耦合应力填入响应面试验表,运用响应面分析软件对该实验表中的数据进行分析。得到TSV 互连结构最大热扭耦合应力值Y与铜柱直径X1、铜柱高度X2、SiO2层厚度X3的回归分析方程如式(1)所示。对于该模型来说,其概率P远小于0.05,表示该模型具有显著性[13]。

为了验证式(1)回归模型具有较好的拟合性,对该模型的相关评价指标进行分析,结果如表5 所示。相关系数(R2)表征回归方程的拟合性,其值越接近1表明拟合度越高[13]。由表5 可知,相关系数为0.9846,表明回归模型具有较好的拟合性能,即热扭耦合应力的仿真值与回归方程预测值相差较小。校正决定系数为0.9648,预测系数为0.7534,表明回归方程具有较好的预测性能,能够对表4 中的数据进行预测。信噪比值通常大于4,本试验中该值为19.6909,表明该回归模型能够真实反映试验结果。

表5 响应面分析结果Tab.5 Response surface analysis results

3.3 基于模拟退火算法的TSV 互连结构参数优化

模拟退火算法(Simulated Annealing,SA)来源于固体退火原理,是一种基于概率的算法[14]。模拟退火算法的优点在于不管函数形式多复杂,其都能以较大概率找到全局最优解。

将响应面法得到的回归方程作为目标函数,利用Matlab 软件完成模拟退火算法的编程,对该目标函数进行全局最优解搜索。对铜柱直径X1、铜柱高度X2、SiO2层厚度X3等影响TSV 互连结构热扭耦合应力的因素设置约束条件如下:30 ≤X1≤50,65 ≤X2≤85,3 ≤X3≤5;并对模拟退火算法中的相关参数进行设置,其中迭代次数为500 次,容差即终止条件设为1×10-100,初始温度为100 ℃,降温函数采用指数降温函数,表达式如式(2)所示:

式中:T为当前温度;T0为初始温度;k为退火参数。

运行该程序得到最优解目标函数值历程曲线和最优参数水平组合,如图8 所示。由图8 可知,在迭代次数不断增大的过程中,该目标函数值收敛明显,迭代刚开始时,目标函数值下降速度快,说明优化好。目标函数值在迭代次数达到100 次左右时下降到最小,之后的目标函数值曲线保持一条直线不再变化,表明不能得到更优的解。优化得到的最优TSV 互连结构参数组合为:X1=50 μm,X2=85 μm,X3=3 μm,即铜柱直径为50 μm,铜柱高度为85 μm,SiO2层厚度为3 μm,得到目标函数最优解为228.704 MPa,该最优解与表4 中所示的最小值257.2 MPa 相比减小了28.496 MPa,达到了TSV 互连结构参数优化的目的。

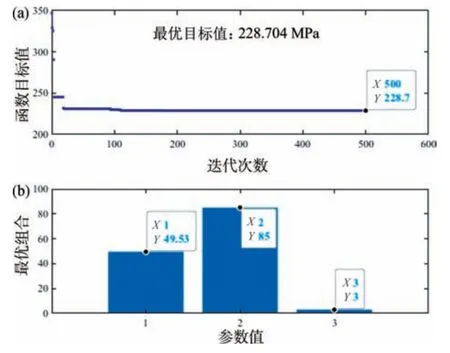
图8 (a)最优解目标函数历程曲线与(b)最优参数组合Fig.8 (a) The optimal solution objective function history curve and (b) the optimal parameter combination

3.4 最优TSV 互连结构参数水平组合验证

基于响应面法、模拟退火算法得到了TSV 互连结构最优参数水平组合: 铜柱直径为50 μm,铜柱高度为85 μm,SiO2层厚度为3 μm。为了验证该最优参数水平组合的准确性,对最优参数水平组合下的有限元模型施加热扭复合载荷,得到TSV 互连结构的最大热扭耦合应力[15]如图9 所示。

图9 最优参数水平组合TSV 互连结构应力云图Fig.9 Stress nephogram of TSV interconnect structure with optimal parameter level combination

由图9 可知,TSV 互连结构最大热扭耦合应力值为243.54 MPa,与试验组合表4 中的应力最小值257.2 MPa 相比减小了13.66 MPa,优化后的TSV 互连结构最大热扭耦合应力下降了5.3%,达到了降低TSV 互连结构应力和优化TSV 互连结构参数的目的,实现了提高TSV 互连结构可靠性的目标。

4 结论

本文通过对三维堆叠封装硅通孔互连结构在热循环与扭转耦合加载条件下的有限元分析,得到以下结论:

(1)TSV 互连结构应力应变随温度循环变化而变化,最大应力应变在每次热循环后均有较小的增加。热扭耦合加载下的TSV 互连结构在低温阶段的应力应变较高温阶段大得多,最大应力应变出现在低温保温结束时刻,且最大应力应变位于铜柱与微凸点接触面外侧,表明该处会率先产生疲劳损伤,破坏TSV 互连结构,影响整个封装体的可靠性。

(2)由单因素分析可知,微凸点材料为SAC387时,TSV 互连结构热扭耦合应力最大,微凸点材料为Pb37Sn63 时,其应力最小;TSV 互连结构最大热扭耦合应力随SiO2层厚度的增大而增大,随铜柱直径的增大而先增大后减小,随铜柱高度的增大而减小。

(3)经优化分析得到TSV 互连结构参数的最优水平组合: 铜柱直径为50 μm,铜柱高度为85 μm,SiO2层厚度为3 μm,并对该最优水平组合进行仿真验证,表明该最优水平组合实现了对TSV 互连结构最大热扭耦合应力和TSV 互连结构参数的优化。