电池储能系统SOC 神经网络融合估计方法

孙玉树 ，李宏川 ，王波 ，贾东强 ，裴玮 ，唐西胜 †

（1.中国科学院电工研究所，北京 100190；2.中国科学院大学，北京 100049；3.国网北京市电力公司，北京 100031）

截至2022 年底，中国已投运的电力储能累计装机达59.4 GW，同比增长37%.其中，新型储能累计装机规模首次突破 10 GW，超过2021年同期的2倍，达到12.7 GW.电池储能作为重要的灵活性调节资源，占据新型储能的主导地位，在提高新能源消纳、提升可靠供电等方面具有积极作用，是构建新型电力系统不可或缺的组成部分［1］.

在电池市场规模日益扩大的背景下，荷电状态（State of Charge，SOC）估计等相关研究越来越得到人们的重视.如果未对电池储能系统SOC 进行精准估计，可能会导致起火、爆炸等事故的发生，危及储能电站甚至电力系统的安全稳定运行.因此，高精度、快速实时的SOC 估计是保障电池运行安全、延长使用寿命的核心技术，对电池更大规模的应用，特别是电站级电池储能系统安全经济运维，具有重要的实用价值［2-3］.

在电池实际应用中，其表现出非线性、时变性、影响因素复杂性和不确定性等特征，造成了SOC 估计难度大、精度不高和适应能力不足，由此产生了较多SOC估计算法及其改进策略.

1）基于经验的估计算法：罗勇等［4］提出的带容量修正的安时积分法，可用于SOC 的实时估计或作为评价其他SOC 估计策略的基准.Xing 等［5］将锂电池进行长时间静置，测量其开路电压和SOC，拟合出两者之间的函数关系，实现对锂电池SOC 估计.上述开环估计算法原理简单、容易实现且计算复杂度低，但常需要满足许多前提条件，且因为缺少反馈环节，算法鲁棒性较差.

2）基于模型的估计算法：Liu 等［6］基于电化学单粒子模型，设计了终端电压反馈注入非线性观测器来监测锂离子电池的SOC.张宵洋等［7］提出了基于分数阶模型自适应扩展卡尔曼粒子滤波的SOC 估计方法.Fu 等［8］建立了Thevenin 模型，采用线性卡尔曼滤波器进行参数在线辨识.杜常清等［9］基于戴维南电池模型，提出一种卡尔曼滤波与扩展卡尔曼滤波相结合的算法估算SOC.Bai 等［10］考虑到温度变化对锂离子电池荷电状态估计的影响，提出了一种基于自适应双扩展卡尔曼滤波的荷电状态估计方法.上述电化学模型虽能较好地表征电池内外部特性，但其辨识较为复杂；等效电路模型结构清晰，参数易于辨识，但模型精度与复杂度难以兼顾，无法反映电化学微观过程.

3）基于数据的估计算法：王语园等［11］提出了基于最小二乘支持向量机机器学习的锂离子电池SOC估计模型.Fan等［12］提出了一种基于U-Net架构卷积神经网络的SOC 估计方法，该方法可以处理变长输入数据和输出等长SOC 估计结果.Gong 等［13］提出了一种基于深度学习的新型深度神经网络模型，该模型以10 s 采样率的电池电压、电流和温度组成的数据单元为输入，SOC 估算值为输出.Chen 等［14］提出了一种基于扩展输入和约束输出的长短期记忆和循环神经网络用于电池SOC 估计.上述基于数据驱动的SOC 估计方法仅依靠系统输入与输出间的映射关系即可建立SOC 估计模型，极大地简化了电池建模过程，但需要大量数据集进行训练来建立各变量之间的关系，精度依赖训练数据集质量，且计算量大.

4）模型数据混合估计算法：单独使用上述3 类方法可能会影响SOC 估计精度或估计速率，因此，多类方法融合估计方法也得到了快速发展，通过优势互补取得更为准确的SOC 估算结果.杨帆等［15］基于二阶Thevenin 等效模型，提出一种将无迹卡尔曼滤波与BP 神经网络相结合的SOC 估计方法.Cui 等［16］提出了一种基于改进的双向门控循环单元网络和无迹卡尔曼滤波的混合方法来实现不同温度下电池SOC的实时稳定估计.

上述研究主要侧重电池单体的SOC 研究，对系统级的分析较少，电池储能系统较电池单体数据量大，运行影响因素众多，数据在线获取难度大，SOC估计的映射关系更为复杂等，因此本文应用数据驱动的方式进行电池储能系统的SOC 估计.首先，对比分析了不同神经网络对电池储能系统SOC 估计的结果；进而利用不同的相关性评价指标筛选对电池储能系统SOC 估计影响较大的特征因素；最后，利用经验模态分解和样本熵对电池储能系统进行分频处理，并利用不同的神经网络对不同频段数据进行估计，从而提高电池储能系统SOC估计的精度和速度.

1 长短时记忆神经网络

由于递归神经网络在训练过程中容易发生梯度爆炸或消失，长短时记忆（Long Short-Term Memory，LSTM）神经网络［17］应运而生，其优势是在网络中引入遗忘门，和传统递归神经网络相比，其更擅长处理长时间尺度历史信息.所添加的遗忘门，会选择性地遗忘和记忆某些历史信息，当其输出值接近0，则说明某些历史信息被选择忘记；当输出值接近1，则倾向于保留记忆更多的历史信息.故，LSTM 避免了部分信息的简单重复覆盖，能够有效解决递归神经网络容易梯度爆炸或消失的问题.LSTM 网络结构如图1所示.

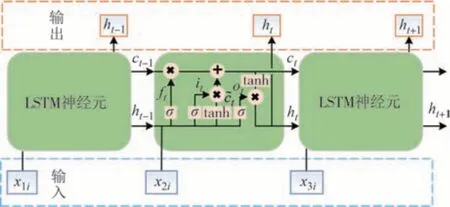
图1 LSTM神经网络结构Fig.1 LSTM neural network structure

式中：式（1）为遗忘门的更新；式（2）为输入门的更新；式（3）为状态门的更新；式（4）为输出门的更新；xt为输入数据，如温度、电压、电流等；ft为遗忘门输出；w、b为各层神经元的权系数，表示输入层输出；ct为卷积层输出；ot为输出层输出；ht为最终输出数据.

2 电池储能系统SOC估计

为了分析不同因素对电池储能系统SOC 的影响，选取国内某储能电站系统的总电压、电流、绝缘电阻、平均电压、平均温度和累计充电电量6 个参量进行SOC 状态估计（如图2～图7 所示），采样间隔为1 min，时长为5 760 min.

图2 总电压Fig.2 Total voltage

图3 电流Fig.3 Current

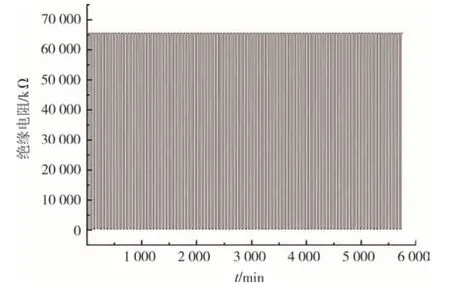
图4 绝缘电阻Fig.4 Insulation resistance

图5 平均电压Fig.5 Average voltage

图6 平均温度Fig.6 Average temperature

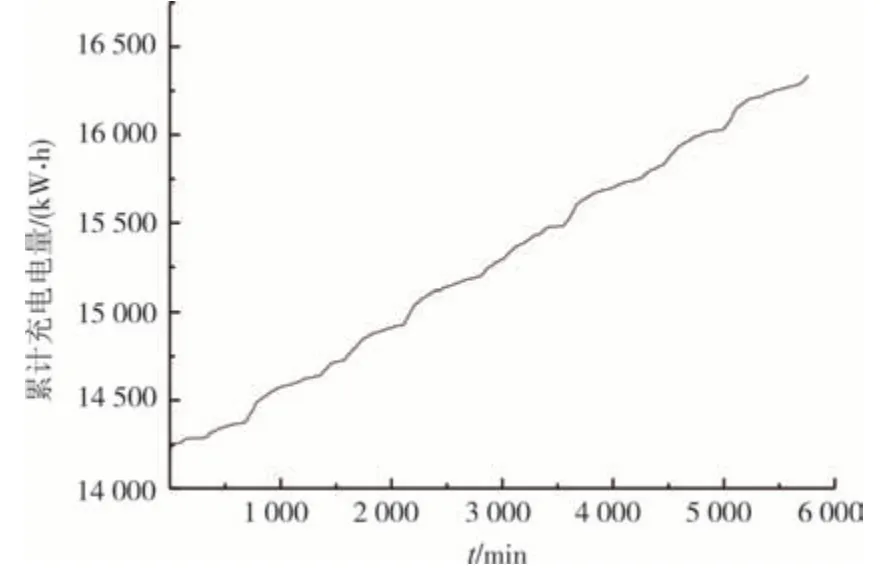
图7 累计充电电量Fig.7 Cumulative charge quantity

为了更好地利用神经网络算法对SOC 进行估计，需对样本数据进行预处理，以防止较大的梯度更新.本文采用离差标准化，将输入和输出数据进行线性变化，使其取值在［0，1］之间.

式中：s为某一输入样本；max(s)为输入样本的最大值；min(s)为输入样本的最小值；d为归一化后数据值.

为了评价电池储能系统SOC 的估计精度，采用均方根误差（Root-Mean-Square Error，RMSE）进行表述，计算公式如下所示.

2.1 不同神经网络算法对比

为了分析不同神经网络算法对估计结果的影响，利用BP神经网络、GRU神经网络和LSTM神经网络对电池储能系统SOC 进行估计，采用前80%作为训练数据，后20%作为测试数据.电池储能系统的SOC 曲线如图8 所示，利用6 个输入参数估计的BP结果如图9 所示，GRU 结果如图10 所示，LSTM 结果如图11所示.

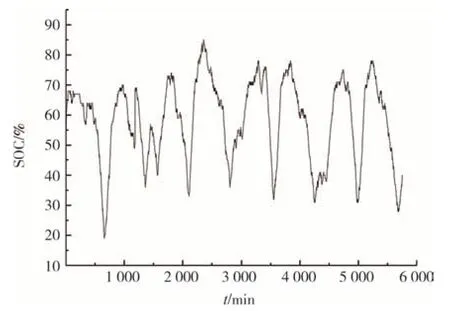
图8 电池储能系统SOCFig.8 Battery energy storage system SOC

图9 BP神经网络估计结果Fig.9 BP neural network estimation results

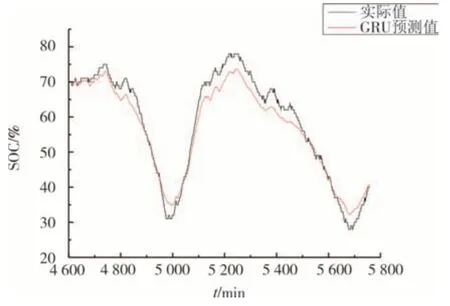
图10 GRU神经网络估计结果Fig.10 GRU neural network estimation results

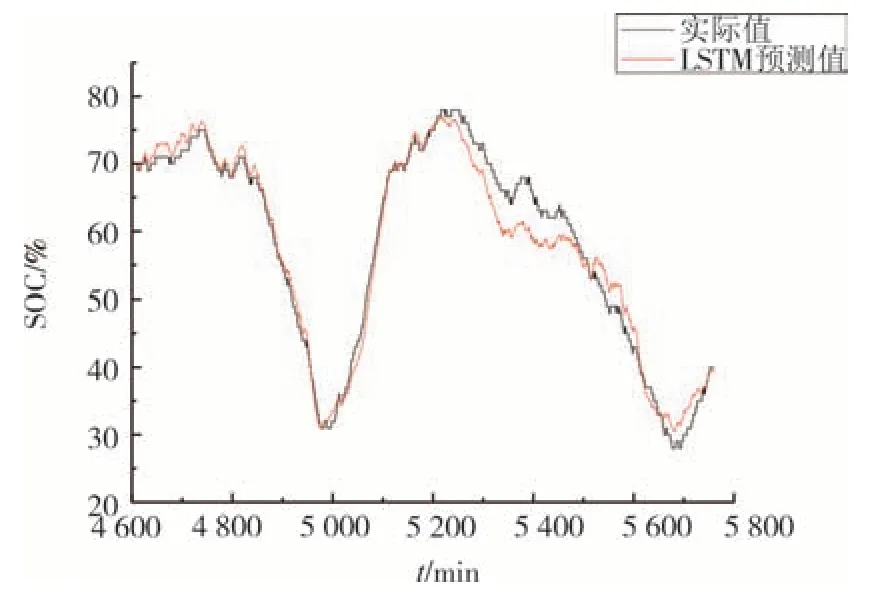
图11 LSTM神经网络估计结果Fig.11 LSTM neural network estimation results

表1 给出了3 种算法的RMSE 和计算时间，可以看出，LSTM 的RMSE 最小，为0.040 2；而BP 计算时间最短，仅需要2.12 s；GRU 的RMSE 和计算时间均处于中间值.因此，基于BP 和LSTM 各自的优势，本文以两者的融合方法进行电池储能系统SOC 的估计.

表1 不同算法的估计结果Tab.1 Estimation results of different algorithms

2.2 SOC估计影响因素

为了分析不同因素对电池储能系统SOC 估计的影响程度，本节分析总电压、电流、绝缘电阻、平均电压、平均温度和累计充电电量6 个指标与SOC 的相关性.为了增强对比性，采用KL 散度、皮尔逊相关系数和灰色关联度进行输入指标与SOC 的相关性分析.

2.2.1 KL散度

KL（Kullback-Leibler）散度［18］，也称相对熵，能够度量2个过程概率分布的差别.设p(x)、q(x)表示2个过程的概率，则KL距离为：

进而p(x)、q(x)之间的KL散度为：

KL 散度是对2 个过程概率分布夹角的度量，数值越大，说明差别越大；反之，越小；当2 类概率分布完全相同时，数值为0.

当求X={x1，x2，…，xn}和Y={y1，y2，…，yn}间的KL散度时，假定概率分布分别为p(x)、q(x).

首先，计算信号X的概率分布，本文采用非参数估计法求解概率分布：

式中：p(x)为核密度估计后的概率密度函数；h为给定的正数，称为窗宽或平滑参数；K(·)为核函数，常用高斯核函数.

同理，可以得到Y的概率分布q(x).

将p(x)、q(x)代入式（7）求解X和Y的KL 距离(p，q)和(q，p)，进一步利用式（8）计算出KL 散度值D(p，q).

利用KL 散度分析不同输入（总电压、电流、绝缘电阻、平均电压、平均温度、累计充电电量）和输出SOC的关联程度，如表2所示.总电压的KL散度值最小，平均电压的KL 散度值最大，即总电压和SOC 的关联程度最高，平均电压和SOC 的关联程度最低，关联度重要性从高到低排序依次为总电压-＞电流-＞累计充电电量-＞绝缘电阻-＞平均温度-＞平均电压.

表2 不同输入参数和SOC的KL散度Tab.2 KL divergence for different input parameters and SOC

2.2.2 皮尔逊相关系数

皮尔逊相关系数［19］广泛用于度量两个变量之间的线性相关程度

当γ＞0 时，表示两变量正相关；γ＜0 时，两变量为负相关；当γ=0 时，表示两变量无线性相关关系.当|γ|=1 时，表示两变量为完全线性相关，即为函数关系；当0 ＜|γ|＜1 时，表示两变量存在一定程度的线性相关.且|γ|越接近1，两变量线性关系越密切；|γ|越接近0，表示两变量的线性相关越弱.

利用皮尔逊相关系数分析6 个输入和输出SOC的相关性，分析结果如表3 所示，其中平均电压的皮尔逊相关系数绝对值最大，电流的最小，关联度重要性从高到低依次为平均电压-＞总电压-＞平均温度-＞累计充电电量-＞绝缘电阻-＞电流.

表3 不同输入参数和SOC的皮尔逊相关系数Tab.3 Pearson correlation coefficients for different input parameters and SOC

2.2.3 灰色关联度

灰色关联度［20］通过分析不同曲线的几何接近性评估它们之间的关系，接近性越高，说明相关性越紧密.

假定参考序列X0和比较序列Xk分别表示为：

式中：n为样本数量；x0(n)和xk(n)均为样本数据.

初始化X0和Xk，以减少参数在维度上的差异：

假定ξi(h) 为Y0和Yk在h时刻的灰色关联系数，则：

式中：ρ为分辨系数，本文取0.5.故，Y0和Yk的灰色关联度为：

式中：i=1，2，…，n；h=1，2，…，Q.

利用灰色关联度分析6 个输入和输出SOC 的相关性，分析结果如表4 所示，其中总电压和平均电压的数值相同，且最大，电流的最小，关联度重要性从高到低依次为平均电压=总电压-＞平均温度-＞累计充电电量-＞绝缘电阻-＞电流.

表4 不同输入参数和SOC的灰色关联度Tab.4 Grey correlation for different input parameters and SOC

由于LSTM 对时序数据的估计精度较高，利用LSTM 进行电池储能系统SOC 估计，在6 个输入中，每次删除一个输入因素，分析不同因素缺失对电池储能系统SOC 估计精度的影响，分析结果如表5 所示.在某一因素缺失的情况下，得到的RMSE 越大，说明该因素对SOC 估计精度影响越大，反之较小.由此可以获得，不同因素的重要性从高到低排序依次为电流-＞总电压-＞平均电压-＞平均温度-＞累计充电电量-＞绝缘电阻.

表5 LSTM估计结果Tab.5 LSTM estimation results

综上所述，在进行影响因素重要性分析时，虽然KL 散度、皮尔逊相关系数和灰色关联度均能够一定程度上反映某个因素的重要程度，但还应以LSTM 等方法实际分析结果为主.本文数据中电流和总电压删除时，RMSE 相近且最大，而在电池储能系统实际运行当中，电流和总电压的变化也是系统电量变化的主要因素，所以两者是电池储能系统SOC 估计中的最关键因素.

3 多神经网络融合策略

目前，大多数神经网络估计方法主要采用单一模型，在对不同研究主体进行分析时，很难一直保持良好的性能，为此，本文采用多种神经网络融合方法进行电池储能系统SOC 估计.首先，利用经验模态分解算法将需要估计的数据进行多时间尺度分解，然后利用样本熵进行复杂性分析，将复杂性相似的分量进行分类聚合，进而利用不同的神经网络算法进行估计.

3.1 经验模态分解算法

经验模态分解（Empirical Mode Decomposition，EMD）算法［21］不需要预先定义基函数，只需根据信号自身的时间尺度特征进行分解，即可获取局部化特征，非常适用于处理非线性非平稳随机信号.

EMD将信号序列分解为一系列关于时间轴对称的固有模态函数（Intrinsic Mode Function，IMF）ci(i=1，2，…，n)与剩余趋势分量rn.IMF须满足以下条件：1）在整个数据序列内，极值点与过零点个数相等或相差不超过1；2）在任一时间点上，局部均值为零.满足以下要求之一即终止分解：1）ci或rn小于预定值；2）rn变为单调函数，不再能获取固有模态函数.综上，信号x(t)经EMD分解后的表达式为：

利用EMD 算法对图8 中的SOC 曲线进行分解，分解后曲线如图12 所示，共12 个IMF 分量和1 个残余分量.从IMF1 到IMF12，频率依次减小，残余分量单调递减.

图12 IMF和残余分量Fig.12 IMF and residual component

3.2 样本熵

近似熵只需较少的数据就可以度量序列的复杂性，但由于存在固有的对自身数据段的比较，所以计算时会产生偏差，且其取值与数据长度有关，一致性较差.由此，精度更高的样本熵［22］被提出，数据序列越复杂，样本熵值就越大，反之，越小，原理如下：

假设时间序列{xi}为x(1)，x(2)，…，x(N)（N为数据量）：

1）将序列{xi}按顺序组成m维矢量，即X(i)=[x(i)，x(i+1)，…，x(i+m-1)]，其中i=1，2，…，N-m+1.

2）定义X(i)与X(j)之间的距离dm(X(i)，X(j))为两者对应元素差值最大值：

对于每一个i值计算X(i)与其余矢量X(j)(j=1，2，…，N-m+1&j≠i)之间的dm(X(i)，X(j)).

3）给定相似容限r(r＞0)，统计每一个i值dm(X(i)，X(j)) ＜r的数量，然后计算其与距离总数N-m的比值，记为(r)：

式中：j=1，2，…，N-m+1&j≠i；num为dm(X(i)，X(j))＜r数量.该过程定义为X(i)模板匹配过程；(r)表示任一个X(j)与模板的匹配概率.

5）增加维数为m+1，重复步骤1）～步骤3），则Bm+1(r)的平均值为：

由此可获取样本熵定义：

当N取有限值时，样本熵估计值为：

样本熵的取值与m、r有关，但其一致性较好，熵值的变化趋势不受m和r的影响，本文取m=2，r=0.2SD（r一般为0.1～0.25SD，其中SD为时间序列的标准差）.

利用样本熵计算每一个IMF 分量的值，如图13所示.随着IMF 分量频段频率的降低，样本熵数值大致呈逐渐降低趋势，即随着频率的降低，数据的波动变小，复杂度降低，自相似度较好.IMF1～IMF5 具有较大的样本熵值，在IMF5 与IMF6 之间样本熵大幅度降低，IMF6～IMF12 具有较小的样本熵值，且大致线性降低，数值均小于0.1；另外，求取样本熵平均值为0.302 8，IMF1～IMF5的样本熵值在平均值之上，而IMF6～IMF12 数值均在平均值之下.因此将SOC 曲线分为两个频段，高频段由IMF1～IMF5 这5 个分量组成，低频段由IMF6～IMF12 这7 个分量加残余分量组成.高频段如图14所示，低频段如图15所示.

图13 各IMF分量的样本熵Fig.13 Sample entropy of each IMF component

图14 高频段Fig.14 High-frequency section

图15 低频段Fig.15 Low-frequency section

3.3 多时间尺度神经网络SOC估计

基于Thinkpad T14 的MatlabR2022a 软件，利用BP 和LSTM 两种策略分别对高、低频段进行估计，估计结果如表6 所示.其中BP 的神经元数为5；LSTM最大轮数为1 500，最小批次为800，初始学习率为0.01，学习率折扣为0.8.BP 对高频分量进行估计时，其精度大幅度提高，RMSE 仅为0.046 3；对低频分量进行估计时，RMSE 为0.152 9；估计后的高频分量和低频分量进行重构，由于数据之间的互补性，重构后的RMSE 为0.144 2.由此可以看出分段估计的方式比直接估计的精度要高.基于LSTM 时，高低频段的估计误差和直接估计类似，但重构后，整体的估计精度有一定程度的提高.由此可见，SOC 分频段后，每个频段的规律性增强，采用相同神经网络算法进行估计时，其精度会有一定程度的改善；再加上估计频段重构后，其数据存在一定程度上的互补性，重构后的数据精度也会提高.

表6 不同算法的高低频段估计结果Tab.6 High and low frequency band estimation results of different algorithms

为了进一步验证分频段估计的优势，采用BP 对高频分量进行估计，如图16 所示；利用LSTM 对低频分量进行估计，如图17 所示；两者组合估计后进行数据重构，如图18 所示.从表7 可以看出，不同神经网络相结合，也能够提高SOC 估计的精度，因此，采用分频段估计相比直接估计能够提高SOC 的估计精确度；再者，从计算时间来看，BP 进行高频估计耗时0.167 2 s，LSTM 进行低频估计耗时235.18 s，两者共耗时约为235.35 s，相比LSTM 不分频估计时的373.75 s，节约37.03%的时间.

表7 组合算法估计结果Tab.7 Prediction results of combinatorial algorithm

图17 基于LSTM的低频分量估计结果Fig.17 Low frequency component estimation results based on LSTM

图18 BP与LSTM组合估计结果Fig.18 Combined estimation results of BP and LSTM

4 结论

针对电池储能系统状态精准估计问题，提出了基于深度学习融合的SOC 估计方法.首先，对比分析了BP、GRU 和LSTM 对电池储能系统时序数据的估计效果；然后，利用KL 散度、皮尔逊相关系数和灰色关联度分析不同输入参数与SOC 的关系，三种相关性分析方法虽然各自能够在一定程度上反映某个输入参量的重要性，但在实际应用中还应以LSTM 估计的结果为准；再者，利用经验模态分解算法将SOC 分解为多个IMF 分量，利用样本熵将其分成高低两个频段，并应用BP 和LSTM 神经网络算法对两个频段分别估计，融合算法比单一算法估计精度至少提升5%，比单一LSIM 算法计算时间节约37.03%，从而为电池储能系统的规模化应用提供参考.