基于无人机5G高空基站的低成本应急定位方法

郑 迪，谢亚琴，谷天园

(南京信息工程大学 电子与信息工程学院，江苏 南京 210044)

0 引言

当城市重特大自然灾害发生时,一般会导致固定基站大面积损毁,使得基于固定基站的定位方法无法满足应急场景下的目标定位要求。文献[1-3]研究了在灾后基于无人机基站(Unmanned Aerial Vehicle Base Station,UAV-BS)来组建公共安全通信网络,提出了一种整合无人机和卫星的应急通信网络架构,在保证多媒体业务的服务质量的同时,大幅度提高了UAV-BS的吞吐量。文献[4]提出了一种将无人机作为空中5G基站并将其与卫星网络进行连接的航天-空-地一体化网络(Space-Air-Ground Integrated Network,SAGIN)。与卫星相比,无人机具有可调节、机动性强等优势。借助SAGIN,将无人机视为传输信号的补充定位节点,可以为待测用户(User Under Test,UT)提供定位服务。

利用无人机搭载空中基站来探测待测目标的方式可以分为有源探测定位和无源探测定位。有源探测定位主要通过移动基站主动发射的电磁波来实现对待测目标的定位,该方法的优点是定位速度快、定位精度高,且定位性能不易受天气与季节的影响。但是,此类设备由于发射功率较大导致能耗较大[5-6],使其难以用于应急通信场景。无源探测定位则是在不主动向外发射电磁波信号的情况下,利用移动基站接收待测目标的电磁波信号,然后提取待测目标定位的相关数据,从而实现待测目标的位置估计[7]。这种无源探测定位技术具有覆盖范围广、隐蔽接收且节省能耗等优点,能够有效提高探测系统的生存和实用性。因此,无源探测定位技术在应急通信、敌我电子对抗和对非法目标进行监测等领域中均有重要的作用[8]。

目前,大量文献对基于无源定位方法获得待测目标的位置展开了研究。无源定位分为基于测距的定位方法和非测距的定位方法,然而基于信号接收强度(Received Signal Strength,RSS)[9-10]构建指纹库以及基于机器学习[11-12]算法进行定位等非测距定位方法的定位精度不高,因此,本文主要研究基于测距的定位方法。文献[13]提出了一种基于到达时间(Time of Arrival,TOA)的定位技术,利用待测目标发射的电磁波信号到达基站的时延,将其转换为距离信息进行目标定位。但是,在三维空间内对待测目标进行定位至少需要4个基站[14]。为了降低应急通信场景下目标定位对基站数量的需求,Kim等[15]提出了虚拟锚点定位法,使用3个基站结合一个虚拟基站对待测目标进行定位。虽然虚拟锚点法计算速度快,但其定位精度不高。为了提高该方法的定位精度,Norrdine[16]提出了代数(Algebraic,ALGEB)算法,但是,该方法仍然不能满足应急场景下的定位精度需求。文献[17]提出了一种基于三维大规模水下无线传感器网络(Underwater Wireless Sensor Networks,UWSNs)的最大定位速率算法,利用测量得到的TOA以及俯角(Angle of Depression,AOD)将基站从三维空间投影到二维空间,然后利用最大定位算法对待测目标进行位置估计。但是,该方法需要结合投影后的基站与待测目标之间的位置关系来进行定位,计算复杂度较高。

基于信号到达角(Angle of Arrival,AOA)的定位技术[18-20]利用高精度测向设备获得待测目标信号的AOA信息,然后将测得的多个方位角的测向线交点作为目标位置的估计值。该方法简单易行,但是随着待测目标与基站之间距离的增大,较小的测角误差也会导致较大的定位误差。文献[21]提出的基于信号到达时间差(Time Difference of Arrival,TDOA)的定位技术则不需要考虑基站与待测目标之间的时间同步问题,主要分为解析类算法[22-23]和迭代类算法[24-25]两大类。解析类算法如Chan算法[23],它通过待测目标到各个基站之间的距离差构建一组关于目标辐射源位置的双曲线方程组,然后进行求解,得到待测目标的估计位置。由于该算法涉及非线性方程组的求解,解析解不易得到,且当TDOA的测量误差较大时,算法的定位性能明显下降。相比于解析类算法,迭代类算法的抗噪声能力更强。即使在TDOA的测量误差较大时,依然能够实现定位。迭代类算法中的泰勒级数展开法[25]通过预先设置待测目标的大致位置,然后逐步迭代不断接近待测目标的真实位置。但是,该方法只有在待测目标的初始位置接近于真实位置时才能够得到较为精准的位置估计,且基站一般为固定的,其移动性和灵活性低,需投入较高的成本。

将TDOA和AOA相融合则可以避免单纯TDOA或AOA方法的不足。文献[26]提出了一种基于牛顿迭代法的联合TDOA/AOA无源定位算法,该方法的定位性能优于基于单一信息的定位算法。为了提升定位精度,Xu等[27]提出了基于被动射频的联合TDOA/AOA定位方法,但是该方法的计算复杂度较高。文献[28]提出了一种基于顺序最小二乘法(Sequential Least Square,SLS)的联合TDOA/AOA无源定位算法,将定位问题转化为SLS优化模型后再使用泰勒级数展开法进行求解。但是,为了获得较为精确的定位性能,该算法需要累积一定的观测值来实现定位。为了能够对待测目标进行实时定位,文献[29]提出了基于加权最小二乘法(Weighted Least Square,WLS)的联合TDOA/AOA无源定位算法,它是在经典Chan算法的基础上加入了方位角信息进行定位。但是,当待测目标和基站之间的距离较远时,该方法的定位精度较低。

在此基础上,本文提出了一种基于无人机5G高空基站的低成本应急定位方法,该方法通过无人机搭载5G高空基站来提供应急通信网络覆盖[30-31]。同时,为了满足应急通信低能耗的需求,移动基站通常处于休眠状态,只有在接近目标需要对其进行精确定位时才开启基站设备,多个移动基站之间通过数据链路实现互联,协同自主地搜索待定位目标[32]。

具体的执行步骤如下:首先,基于最小二乘(Least Square,LS)法对待测目标进行初始定位,并将得到的初始位置设为虚拟移动基站的位置。然后,基于现有基站及虚拟移动基站,再次利用LS算法对待测目标的位置进行估计,并根据求解得到的待测目标位置来更新虚拟移动基站的位置。重复上述更新多次后,得到一组虚拟移动基站集合,利用高程精度因子(Vertical Dilution of Precision,VDOP)来选取一个最佳的虚拟移动基站位置,并基于该最佳虚拟移动基站的位置来更新待测目标的位置信息。接着,将三维空间的移动基站投影到二维水平面,基于TDOA和方位角联合测量构建定位方程,使用WLS算法对待测目标的水平位置进行更新,利用初始解分量之间的相关性,使用二次WLS算法对上述求解的待测目标的水平位置再次进行修正,从而得到待测目标的最终估计位置。

本文的主要贡献如下:①对待测目标进行初始定位,并将得到的初始位置作为虚拟移动基站的初始位置,降低了对基站数量的要求。同时,基于VDOP最小选择最佳的虚拟移动基站,降低了待测目标的定位误差。②利用坐标转换和坐标投影的方法将空中基站投影到二维平面,对待测目标的水平位置再次进行更新。③所提算法可以应用于应急通信场景中,以较低的定位成本获得了较高的定位精度,二维定位误差小于1 m的概率为84.2%,三维定位误差小于2 m的概率为90.9%。

论文的其余部分组织如下:第1节介绍了系统模型;第2节详细介绍了本文所提算法的算法设计;第3节给出了算法仿真结果;第4节对本文进行了总结。

1 系统模型

本文提出的基于无人机的5G高空基站应急定位系统模型如图1所示。

图1 基于无人机的5G高空基站应急定位系统模型Fig.1 UAV-based 5G high-altitude base station emergency positioning system model

当发生灾害导致出现被摧毁的基站(Damaged Base Station,DBS)时,可以利用无人机搭建5G高空基站的方式,为受灾地区的用户提供应急定位服务,图1中UAV-BS1、UAV-BS2、UAV-BS3以及UAV-BS4分别表示1号、2号、3号以及4号无人机。1号、2号和3号无人机组成应急网络为受灾地区用户提供基站服务,该应急网络通过4号无人机和未被摧毁的地面基站(Base Station,BS)建立连接,从而连接到5G核心网,保障应急场景下的定位与通信服务。

图2为简化的应急定位系统模型,地平面为XOY面,高度为Z轴。假设移动基站的位置已知,并设在t时刻,第i个移动基站的位置坐标为ui(t)=[xi(t),yi(t),zi(t)],第i个移动基站相对于待测目标用户的方位角和俯角分别表示为θi(t)和φi(t),i=1,2,…,NB,NB为移动基站总数,则初始基站集合B={u1(t),u2(t),…,uNB(t)}。设待测目标用户在t时刻的位置为s(t)=[x(t),y(t),z(t)],di(t)表示t时刻第i个移动基站与待测目标用户之间的距离,则:

di(t)=‖ui(t)-s(t)‖。

(1)

图2 简化的应急定位系统模型Fig.2 Simplified emergency positioning system model

令r(t)=‖s(t)‖2,则式(1)可以表示为:

A(t)T(t)=b(t),

(2)

式中:

(3)

式中:σi(t)表示第t时刻第i个移动基站与待测目标用户之间的距离测量误差。

当测量误差σi(t)已知时,式(2)中A(t)和b(t)均已知。因此,目标用户的位置估计问题就转化为对式的求解问题。

由于T(t)中含有4个未知量,为了获得待测目标的三维位置信息,则至少需要4个位于不同平面内的移动基站。

2 算法设计

为了减少目标定位对移动基站数量要求,同时保持高精度的定位性能,本文主要讨论利用3个已知移动基站来对目标用户进行定位,即NB=3,此时,移动基站集B={u1(t),u2(t),u3(t)},假设在t时刻,第n次迭代得到的虚拟移动基站vn(t)为:

vn(t)=[xvn(t),yvn(t),zvn(t)],n=0,1,…,Nup,

(4)

式中:Nup表示总迭代次数。

首先,基于虚拟移动基站来确定待测目标的三维初始位置,并基于VDOP最小更新该待测目标的三维位置信息;随后,基于两步投影方法更新待测目标的水平位置信息,具体的算法实施流程如图3所示。

图3 所提算法的实施流程Fig.3 Implementation flowchart of the proposed algorithm

2.1 基于虚拟移动基站确定待测目标的高度

2.1.1 确定虚拟移动基站集

基于虚拟移动基站的应急定位系统模型如图4所示。

图4 基于虚拟移动基站的应急定位系统模型Fig.4 Emergency positioning system model based on virtual mobile base station

由式(2)可得,在t-1时刻:

T(t-1)=[A(t-1)TA(t-1)]-1A(t-1)Tb(t-1),

(5)

式中:

设n=0,将根据式求解得到的目标位置设置为t时刻的虚拟移动基站,即:

(6)

更新移动基站集,得到:

B={u1(t),u2(t),u3(t),vn(t)}。

(7)

将式(6)、式(7)代入式(2)可得到:

A′(t)T(t)=b′(t),

(8)

根据LS法求解式(8)得:

T(t)=[A′(t)TA′(t)]-1A′(t)Tb′(t)。

(9)

将式中的n值加1,同时,将式所求得的T(t)中的第2～4行元素赋值给vn(t),更新虚拟移动基站集为V=V+{vn(t)}。重复式(6)～式(9)Nup次,可得到虚拟移动基站集:

V={v0(t),v1(t),…,vn(t),…,vNup(t)},

(10)

式中:vn(t)=[xvn(t),yvn(t),zvn(t)]=[x(t+n-1),y(t+n-1),z(t+n-1)],x(t+n-1)、y(t+n-1)、z(t+n-1)表示t+n-1时刻求得的待测目标的三维坐标位置。

2.1.2 基于VDOP最小选择最佳虚拟移动基站

由文献[33]可知,待测目标的高程误差可表示为:

mV=VDOP·σ,

(11)

式中:σ表示测量误差,VDOP为高程精度因子,其值大小与多个基站及待测目标所构成的空间几何图形的体积成反比。体积越大,VDOP值越小,空间高程定位误差也越小。

移动基站、虚拟移动基站以及待测目标所形成的空间六面体模型如图5所示。

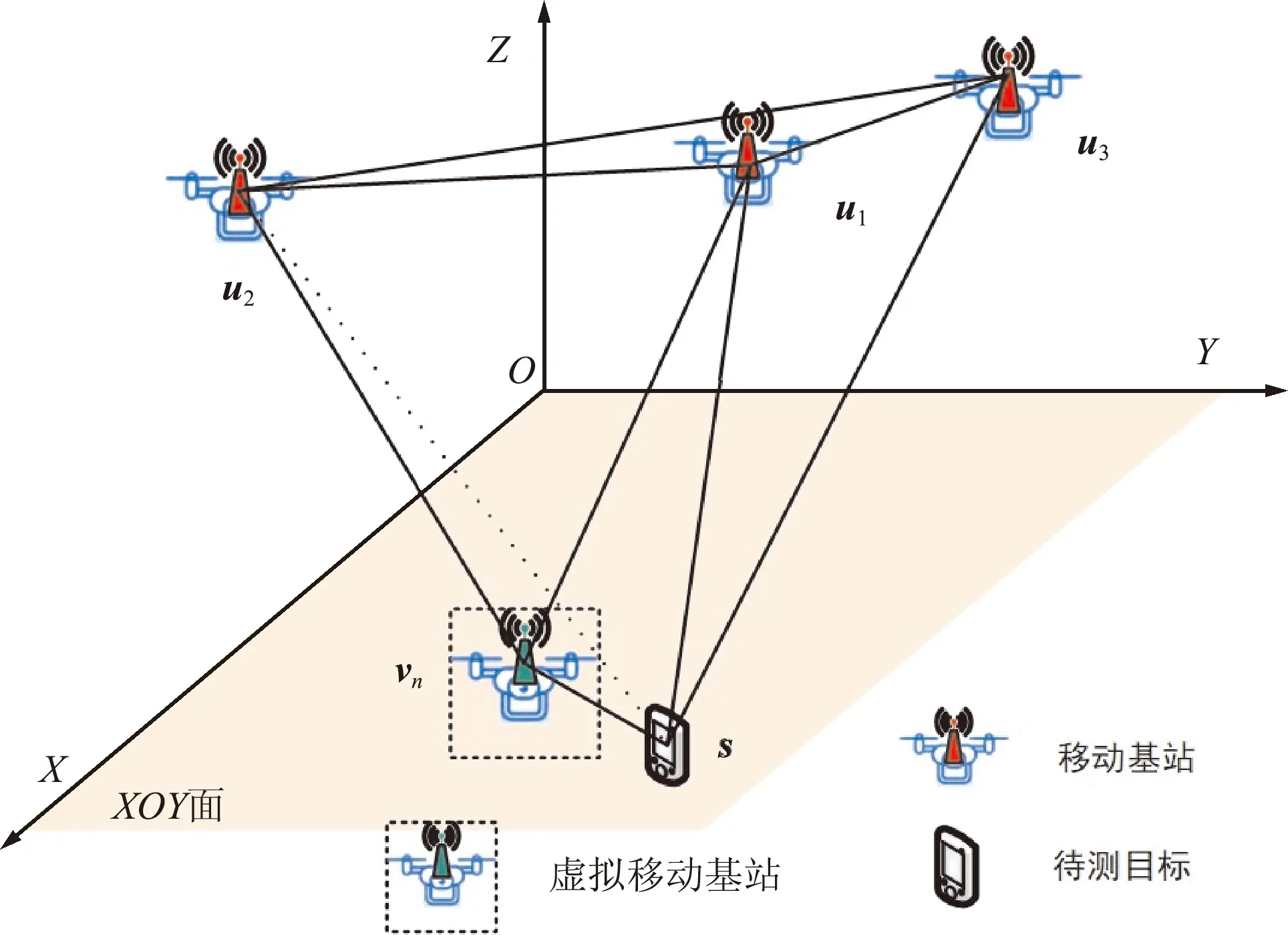
图5 空间六面体模型Fig.5 Space hexahedron model

该六面体的体积可以表示为:

(12)

式中:s=[x,y,z]表示待定位的目标位置,ui=[xi,yi,zi],i=1,2,3表示第i个移动基站的坐标位置,vn=[xvn,yvn,zvn]表示第n次迭代得到的虚拟移动基站的坐标位置。

移动基站、虚拟移动基站和待测目标之间的距离dj可表示为:

(13)

式中:j=1,2,3,vn,n=0,1,…,Nup。

(14)

将式(14)表示为矩阵形式可得:

Δpn=GnΔbn,

(17)

式中:

采用LS法求解式(17)可得:

(18)

通常假设Δpn中各分量分布相同且相互独立,则均方差等于用户等效测距误差(User Equivalent Ranging Error,UERE),用σUERE表示等效测距误差的均方差,得:

(19)

结合式(18)可得:

(20)

因此雅可比矩阵Gn可表示为:

(21)

那么权系数阵Hn可表示为:

(22)

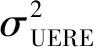
2.1.3 基于VDOP获得高精度的高程信息

根据式(22)可知,高程精度因子VDOPn[34]可表示为:

(23)

分别将虚拟移动基站集V中的Nup+1个虚拟移动基站位置代入式(21),其中:

V={v0(t),v1(t),v2(t),…,vNup(t)}。

(24)

2.2 基于两步投影迭代更新目标的水平位置

2.2.1 三维坐标投影转换

获得待测目标的高精度高程信息后,将三维移动基站投影到水平面,对待测目标的水平位置再次进行更新。移动基站的三维投影模型如图6所示。首先,对坐标进行变换,即将坐标原点移动到待测目标所在位置,则坐标变换后待测目标的位置坐标表示为s′(t)=[0,0,0],第i个移动基站的位置坐标可表示为:

(25)

然后,将移动基站通过投影到XOY面得到投影移动基站,则t时刻待测目标的二维坐标位置表示为s″(t)=[0,0],t时刻第i个投影移动基站的二维坐标位置可表示为:

(26)

图6 三维坐标投影模型Fig.6 Three-dimensional coordinate projection model

因此,基于TDOA和方位角的联合测量的定位方程可表示为:

(27)

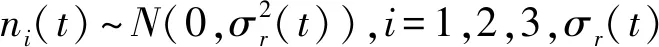
(28)

式中:σθ(t)为方位角的角度测量误差的方差。

根据上式将TDOA方程整理为矢量形式:

(29)

式中:r(t)=[r21(t),r31(t)]为存在噪声误差的TDOA测量值矢量,该矢量是已知的,r′(t)=[r′21(t),r′31(t)]是由3个投影移动基站形成的真实TDOA矢量;r′i1(t)=ri(t)-r1(t),i=2,3为第i个投影移动基站距待测目标距离与u″1(t)投影移动基站距待测目标距离的真实程差,矢量r′(t)是未知的,n(t)=[n21(t),n31(t)]为由3个投影移动基站形成的TDOA测量误差矢量,对应的协方差矩阵Rr(t)可表示为:

Rr(t)=E[nT(t)n(t)]。

(30)

那么误差协方差矩阵R(t)可表示为:

(31)

当移动基站获得的待测目标的方位角的角度测量误差较小时,方位角对应的误差:

(32)

式中:nθ(t)如式(28)所示。

根据式(27)和式(32),基于TDOA和方位角联合测量的定位方程可表示为:

(33)

2.2.2 利用2次WLS算法对待测目标的水平位置进行更新

假设在t时刻,待求未知变量为:

由式(33)得到的待测目标位置对应的误差矢量e1(t)可以表示为:

e1(t)=h1(t)-G1(t)μ1(t),

(34)

式中:

(35)

利用WLS法对式(34)进行求解,可以得到:

式中:Σ1(t)为基于TDOA和方位角联合测量的误差矢量e1(t)的协方差矩阵的逆矩阵,且

式中:B1(t)=diag(r2(t),r3(t)),diag(·)函数用于构造对角矩阵;R(t)表示误差协方差矩阵,如式(31)所示。

根据式(37)计算的结果,μ1(t)的协方差矩阵可以表示为:

(39)

e2(t)=h2(t)-G2(t)μ2(t),

(40)

式中:

利用WLS对式(40)进一步求解,可以得到:

(43)

式中:Σ2(t)为误差矢量e2(t)的协方差矩阵的逆矩阵。

(44)

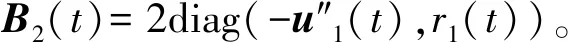
对式(40)中的μ2(t)进行求解后,通过式(42)可以对待测目标的水平位置进一步进行更新,得到更为精确的水平位置信息:

(45)

式中:[μ2(t)]1、[μ2(t)]2分别为μ2(t)的第一、第二个元素。

U(t)=diag(sgn([[μ2(t)]1,[μ2(t)]2]T-[x1(t),y1(t)]T)),

式中:sgn(·)为正负号判断函数。

(46)

3 仿真分析

为了检验本文所提算法对待测目标进行定位的性能,本次仿真使用3个移动基站对待测目标进行协同定位,利用蒙特卡罗模拟进行仿真并对仿真结果进行分析。分别针对UT与移动基站共面和非共面的场景,在相同的仿真参数设置下,将本文所提出的方法与虚拟锚点算法和ALGEB算法进行了对比,分别从测距误差、待测目标与移动基站之间的高程差2个角度来分析其对定位精度的影响。

3.1 UT与移动基站共面场景的仿真分析

3.1.1 共面场景下测距误差对定位精度的影响

在本节分析二维场景下测距误差对定位精度的影响时,固定方位角的角度误差nθ为0.3°,假设在t时刻,3个移动基站及待测目标的坐标位置如表1所示,坐标单位为m。由于移动基站和待测目标的高度一样,此时可以视为三维场景下的一种特殊情况。

表1 3个移动基站及待测目标的坐标位置Tab.1 Coordinate positions of three mobile base stations and the target to be measured 单位:m

图7分别描述了二维场景下本文所提方法、单次WLS算法、ALGEB算法以及虚拟锚点算法的定位误差受测距误差变化的影响。由图7可知,4种方法的整体趋势一致,均方根误差(RootMeanSquareError,RMSE)均随测距误差的增大而增大。当测距误差σ=2.5m时,4种方法的RMSE分别为1.60、1.93、4.25、4.07m。与ALGEB算法比,本文所提算法的定位精度提升了62.35%;与虚拟锚点算法相比,定位精度提升了60.69%;与单次WLS算法相比,定位精度提升了17.10%。因为ALGEB算法和虚拟锚点法都仅利用了时延进行定位,定位精度较低。本文所提方法和单次WLS算法不仅利用时延进行定位,还加入了方位角,可以获得较高的定位精度。而本文所提算法相比于单次WLS算法,使用了2次WLS对定位结果进行校准,使得本文所提算法的定位精度最高。

图7 测距误差σ对定位性能的影响(共面)Fig.7 The effect of ranging error σ on positioning performance(coplanar)

图8比较了二维场景下测距误差σ分别为1、4m时,本文所提方法与虚拟锚点算法、ALGEB算法的定位误差累计分布(CumulativeDistributionFunction,CDF)图。由图8可以看出,当测距误差σ=1m时,本文所提方法、单次WLS算法、ALGEB算法与虚拟锚点算法的定位误差低于1m的概率分别为84.2%、78.7%、32.7%和32.2%。当测距误差σ=4m时,本文所提方法、单次WLS算法、ALGEB算法与虚拟锚点算法的定位误差低于1m的概率分别为39.3%、24%、2.6%和2.4%。因为单次WLS算法相比于ALGEB算法、虚拟锚点算法,加入了方位角信息进行定位,使得其定位能力最强。而本文所提方法由于进行了2次WLS运算,使得其定位能力高于单次WLS算法。

图8 σ=1、4 m时的CDF图(共面)Fig.8 CDF diagram at σ=1, 4 m (coplanar)

3.1.2 共面场景下角度误差对定位精度的影响

为了便于分析二维场景下方位角的角度误差对定位精度的影响,将测量误差σ固定在2m,3个移动基站及待测目标的坐标位置如表1所示。

图9描述了二维场景下在本文所提方法以及单次WLS算法的定位误差受角度误差变化的影响。由图9可知,2种方法的RMSE都随着角度误差的增大而增大。当角度误差nθ为0.3°时,2种方法的RMSE分别1.33、1.58m。与单次WLS算法比,本文所提算法的定位精度提升了15.82%。因为相比于本文所提方法,单次WLS算法没有使用WLS算法进行定位修正,使得抗噪能力弱于本文所提算法,因此定位误差较大。

图9 角度误差对定位性能的影响(共面)Fig.9 Diagram of influence of angle error on positioning performance (coplanar)

图10比较了二维场景下角度测量误差nθ分别为0.1°、0.6°时,本文所提方法与单次WLS算法的CDF图。由图10可知,当nθ=0.1°时,本文所提方法与单次WLS算法的定位误差低于1m的概率分别为67%和52.8%。当角度测量误差nθ=0.6°时,本文所提方法与单次WLS算法的定位误差低于1m的概率分别为53.2%和34%。因为本文所提方法利用WLS对待测目标的坐标进行了修正,使得定位性能优于单次WLS算法。

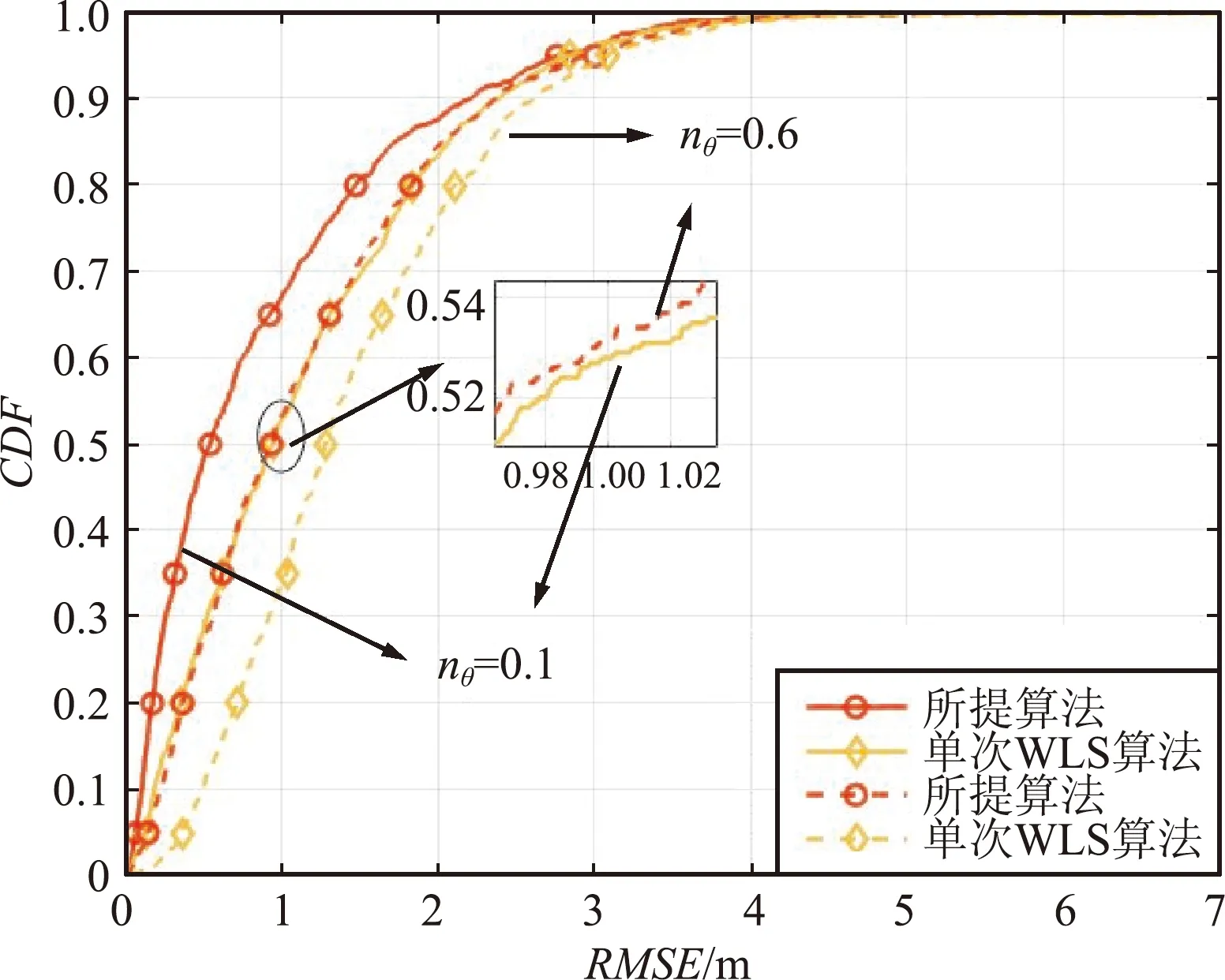
图10 nθ=0.1、0.6时的CDF比较(共面)Fig.10 CDF diagram at nθ=0.1,0.6 (coplanar)

3.2 UT与移动基站非共面场景的仿真分析

3.2.1 非共面场景下测距误差对定位精度的影响

分析三维场景下测距误差对定位精度的影响时,固定方位角的角度误差nθ为0.3°,假设在t时刻,3个移动基站及待测目标的坐标位置如表2所示。

表2 3个移动基站及待测目标的坐标位置Tab.2 Coordinate positions of three mobile base stations and the target to be measured 单位:m

图11描述了三维场景下本文所提方法、ALGEB算法以及虚拟锚点算法的定位误差受测距误差变化的影响。由图11可知,3种方法的整体趋势一致,RMSE均随着测距误差的增大而增大。当测距误差σ=2m时,3种方法的RMSE分别2.55、3.84、7.16m。与ALGEB算法比,本文所提算法的定位精度提升了33.59%,与虚拟锚点算法相比,定位精度提升了64.39%。因为相比于ALGEB算法,本文所提方法不仅加入了方位角,而且使用了2次WLS算法,该方法有效抑制了定位误差,获得了较高的定位精度。而虚拟锚点法由于仅迭代一次,抗噪能力弱于ALGEB算法,因此定位误差最大。

图11 测距误差σ对定位性能的影响(非共面)Fig.11 Effect of ranging error σ on positioning performance (non-coplanar)

图12比较了三维场景下,TDOA的测量误差分别为1、4m时,本文所提方法与ALGEB算法、虚拟锚点算法的CDF图。由图12可知,当σ=1m时,本文所提方法、ALGEB算法与虚拟锚点算法的定位误差低于2m的概率分别为90.9%、65.8%和0.6%。当σ=4m时,本文所提方法、ALGEB算法的定位误差低于2m的概率分别为21%、2.4%,虚拟锚点算法的定位误差低于2m的概率为0。因为ALGEB算法的定位能力强于只迭代一次进行定位的虚拟锚点算法,而本文所提方法由于进行了2次WLS运算,且使用多次迭代计算高程位置信息,因而定位性能最优。

图12 σ=1、4 m时的CDF图(非共面)Fig.12 CDF diagram at σ=1, 4 m(non-coplanar)

3.2.2 目标与移动基站间高程差对定位精度的影响

为了便于分析目标与移动基站间高程差对定位精度的影响,将测量误差σ固定在2m,方位角的角度误差nθ固定为0.3°,3个移动基站的水平面位置信息及待测目标的坐标位置如表2所示。

图13描述了本文所提方法、ALGEB算法以及虚拟锚点算法的定位误差受目标与移动基站之间高程差变化的影响。由图13可知,3种方法的RMSE均随着目标与移动基站之间高程差的增大而增大。当目标与移动基站之间高程差为35m时,3种方法的RMSE分别3.05、4.23、9.15m。与虚拟锚点算法相比,本文所提算法的定位精度提升了66.67%,与ALGEB算法相比,定位精度提升了27.90%。因为虚拟锚点算法没有利用2次WLS算法对水平面位置信息进行更新,使得其抑制定位误差的能力明显没有本文所提方法的能力强。而ALGEB算法的抗噪声能力强于虚拟锚点算法,因此虚拟锚点算法的定位性能最差。

图13 高程差对定位性能的影响Fig.13 Diagram of the effect of elevation difference on positioning performance

图14比较了目标与移动基站之间高程差分别为25、50m时,本文所提方法与虚拟锚点算法、ALGEB算法的CDF图。由图14可知,当高程差为25m时,本文所提方法和ALGEB算法的定位误差低于3m的概率分别为50.2%、36.3%,虚拟锚点算法的定位误差低于3m的概率为0。当高程差为50m时,本文所提方法和ALGEB算法、虚拟锚点算法的定位误差低于3m的概率分别为76.9%、36.3%和1.4%。因为当高程差较小时,移动基站和虚拟移动基站形成的棱锥体积过小,从而导致定位精度不高,因此,虚拟锚点算法的定位能力最弱。而本文所提算法由于对虚拟移动基站的位置进行了迭代,且使用了2次WLS算法提高了水平面位置信息的精度,因此定位性能更好。

图14 高程差分别为25、50 m的CDF比较Fig.14 Comparison diagram of CDF with elevation difference of 25, 50 m respectively

4 结束语

本文对应急通信场景下的待测目标的三维定位问题进行了研究,在突发灾害导致地面基站损毁时,基于无人机5G高空基站提供低成本高精度的定位方案。首先,利用无人机搭载移动基站构建应急通信网;其次,基于虚拟移动基站得到目标的高程位置信息;然后,利用三维投影方法以及TDOA和方位角之间的联合定位,得到待测目标的水平位置信息。仿真结果表明,本文所提算法能够获得更高的定位精度,二维定位误差小于1m的概率为84.2%,三维定位误差低于2m的概率为90.9%。但本文仅在UAV-BS运动幅度不大的情形下进行了研究,下一步工作将在UAV-BS按一定轨迹运动的情形下进行研究。改进的方法对其他移动基站进行三维定位具有一定的参考价值。