基于脉振正弦波注入法的位置估算优化方法

□ 陈瑜程 □ 汤廷孝

宁波大学 机械工程与力学学院 浙江宁波 315211

1 研究背景

永磁同步电机因自身体积小、扭矩大、效率高等优点,在家用电器、工业产品、医疗器械等各种场合被广泛应用[1-2]。在实现高性能控制时,永磁同步电机需要准确的转子位置和转速信息。传统方式是采用机械式位置传感器,如光电编码器、磁编码器、旋转变压器等,来获取相关信息[3],但是这样做会增大驱动平台的体积、质量,增加成本,并降低系统的可靠性,进而限制在一些极端环境中的应用。为了降低对控制系统稳定性的影响,并减少设计成本,无传感器的永磁同步电机控制技术被快速发展起来。

脉振正弦波注入法利用电机凸极效应产生饱和凸极特性,通过将高频信号与基波信号相叠加,注入电机的三相绕组,随之产生的高频响应电流可进行解调,分离包含转子位置误差量的信号。这些信号再经过锁相环后,便可精确地估算出转子位置,从而获得近乎真实的测量结果[4-5]。

传统脉振正弦波注入法在控制系统中使用传统滤波器,可能导致信号提取精度不足、滤波延迟、系统带宽降低等问题。针对这些问题,时维国等[6]运用小波变换技术,解决传统巴特沃斯滤波器无法提取低幅弱信号或提取精度不足的问题。于安博等[7]提出构建无滤波器模型,通过直轴和估计交轴的响应信号,创建不含正弦函数项的位置估计误差新函数。这种方法有效改善了控制系统的动态性能。Bolognani等[8]提出采用离散傅里叶变换来提取高频电流包络线,作为转子位置误差函数信号。相比传统方法,这一方法不需要调制信号的相位,即可实现位置信息提取,从而显著提升位置信息的信噪比。林环城等[9]设计了新的位置观测器,减少滤波器,使参数整定更易实现。Ghule等[10]提出自感知方法,用于分离激励同步电机转子位置。Li Wenya等[11]通过减去采样电流中的高频信号,获得基频反馈电流,减小因高频电流分量引起的转矩脉动。

为了减小传统滤波器带来的相位延迟对系统稳定性的影响,可以将广义二阶积分器运用到位置估算环节中。广义二阶积分器通常具有高频滤波能力强、响应速度快等特点,可以用于模拟电路、信号处理、自动控制等领域[12]。笔者使用广义二阶积分器代替位置估计环节中的带通滤波器和低通滤波器,提出基于脉振正弦波注入法的位置估算优化方法,并通过仿真和试验来验证这一方法的可行性。

2 脉振正弦波注入法原理

永磁同步电机在同步旋转坐标系d轴和q轴上的电压方程可以表示为:

(1)

式中:ud、uq分别为d轴和q轴上的电压;R为定子电阻;id、iq分别为d轴和q轴上的电流;Ld、Lq分别为d轴和q轴上的电感;t为时间;ωe为转子角速度;ψf为永磁体磁链。

(2)

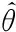
高频电压和电流的关系可以表示为:

(3)

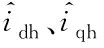
采用脉振正弦波注入法,在估计的同步旋转坐标系的d轴上进行注入。d轴上注入的高频电压信号可以表示为:

(4)

式中:u为注入高频信号的幅值。

将式(4)代入式(3)并化简,可以得到高频注入下d轴和q轴上的电流高频分量为:

(5)

Z=(Zdh+Zqh)/2

(6)

ΔZ=(Zdh-Zqh)/2

(7)

3 传统位置估算方法

(8)

(9)

(10)

式中:|Zdh|、|Zqh|分别为d轴和q轴上的高频阻抗幅值;φd、φq分别为d轴和q轴上的高频阻抗相角。

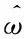
4 位置估算优化方法

4.1 带通滤波器幅值衰减和相位偏移

为了提高基于脉振正弦波注入法的电机控制系统的性能,需要对信号进行处理,以提取转子位置信息。然而,滤波器的使用会导致幅值衰减和相位偏移。假设使用带通滤波器幅值衰减为A0,相位偏移为φ0,得到位置误差公式为:

(11)

为了保持系统稳定,需保持K0为正值。根据公式可知,幅值的衰减不会影响位置误差的正负值,相位偏移则可能会对系统稳定性产生影响。因此,需要进行适当的滤波器设计,以平衡滤波效果和系统性能。

4.2 低通滤波器对带宽影响

低通滤波器的截止频率是影响带宽的主要因素之一。截止频率的选择需要考虑系统需求和稳定性。如果截止频率过低,则会出现相对较大的相位延迟和不稳定性,影响整个系统的带宽。如果截止频率过高,则可能引起电流环的不稳定性和控制精度降低。因此,在设计速度环控制器时,同样需要详细分析实际需求,并合理选择低通滤波器的截止频率。

4.3 广义二阶积分器信号提取优化

带通滤波器和低通滤波器在使用过程中,会出现相位偏移,这会影响系统的动态性能。为了解决传统滤波器所带来的相位延迟问题,采用广义二阶积分器对信号估计部分进行优化。广义二阶积分器是一种非线性滤波器,有能力提取信号中的高频成分,并且不引起相位延迟。广义二阶积分器的工作原理为将输入信号分别与相位相差90°的两个正弦波进行乘积运算,通过带通滤波器后对信号进行差分运算,并对差分结果进行积分,从而获得输出信号[13]。在电机控制系统中,使用广义二阶积分器可以精确提取高频信号,从而提高控制系统的稳定性。广义二阶积分器结构如图2所示。

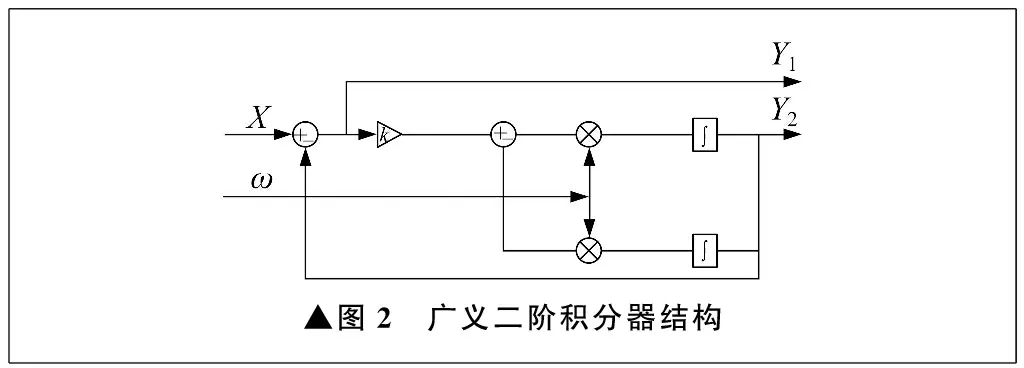
▲图2 广义二阶积分器结构

广义二阶积分器的传递函数可以表示为:

(12)

式中:ω为高频注入信号角频率;k为比例环节因数。

笔者采用G2(S)结构代替传统带通滤波器进行高频信号提取,并使用G1(S)结构代替低通滤波器提取误差信号。比例环节因数k会影响广义二阶积分器滤波器的带宽和响应速度。以G2(S)结构为例,不同k值下广义二阶积分器伯德图如图3所示。

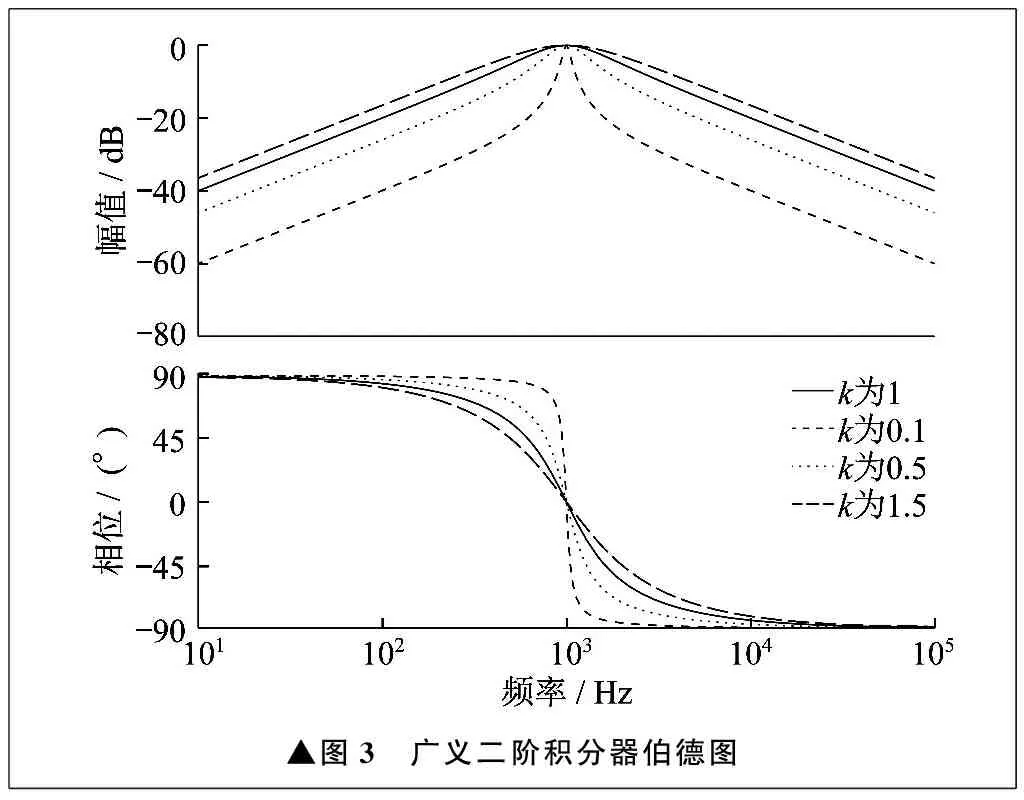
▲图3 广义二阶积分器伯德图

当k取值较小时,广义二阶积分器的带宽较小,能够提高滤波效果,但响应速度相对较慢。反之,当k取值较大时,广义二阶积分器的带宽增大,但滤波效果减弱,响应速度加快。考虑实际应用需求及性能表现,选择k为1作为广义二阶积分器的因数。

通过采用位置估算优化方法,可以克服传统滤波器存在的相位延迟问题,从而显著提高电机控制系统的性能和稳定性。同时,广义二阶积分器的应用还可以保证信号提取的高精度,能够更好地适应不同工况和要求。位置估算优化框图如图4所示。

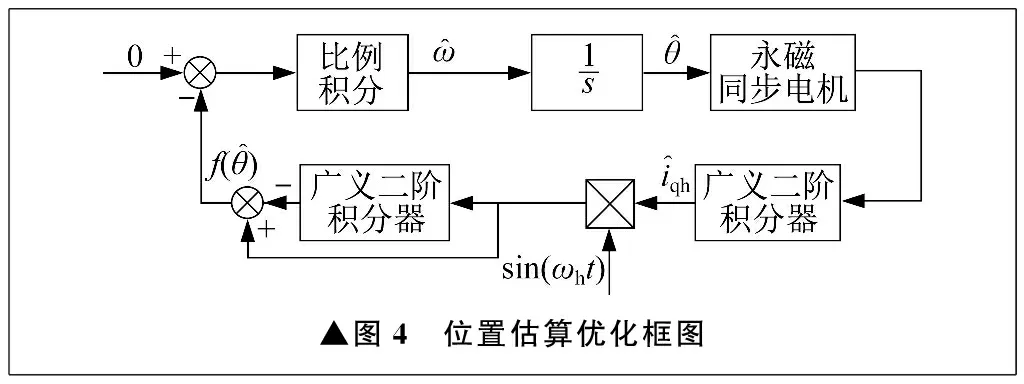
▲图4 位置估算优化框图

5 仿真分析

为了验证所提出的使用广义二阶积分器代替传统滤波器的方法的可行性,在MATLAB/Simulink软件中建立仿真模型。永磁同步电机参数见表1,注入幅值为额定电压10%,即2 V的脉冲正弦波信号,频率为逆变开关频率的1/10,即1 kHz,并选择广义二阶积分器因数为1,对系统进行仿真过程观测。

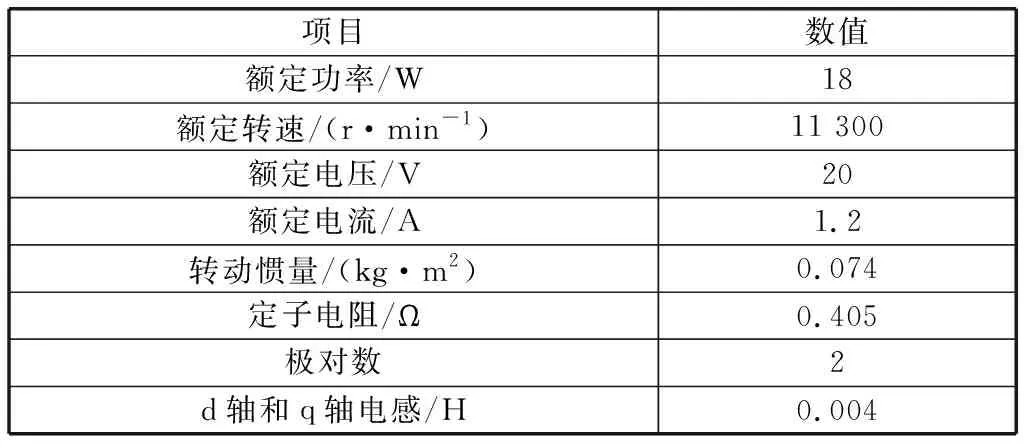
表1 永磁同步电机参数

电机额定转速为600 r/min时,传统位置估算方法及位置估算优化方法的仿真结果分别如图5、图6所示。由图5可知,经过0.4 s运行后,传统位置估算方法达到最大转子位置误差0.2 rad,稳定时转子位置误差保持在0.02 rad左右。由图6可知,位置估算优化方法最大转子位置误差减小至0.12 rad,并且在稳定时转子位置误差减小至0.01 rad。可以看出,位置估算优化方法能够减小最大位置误差约40%,稳态时的转子位置误差也有所减小。

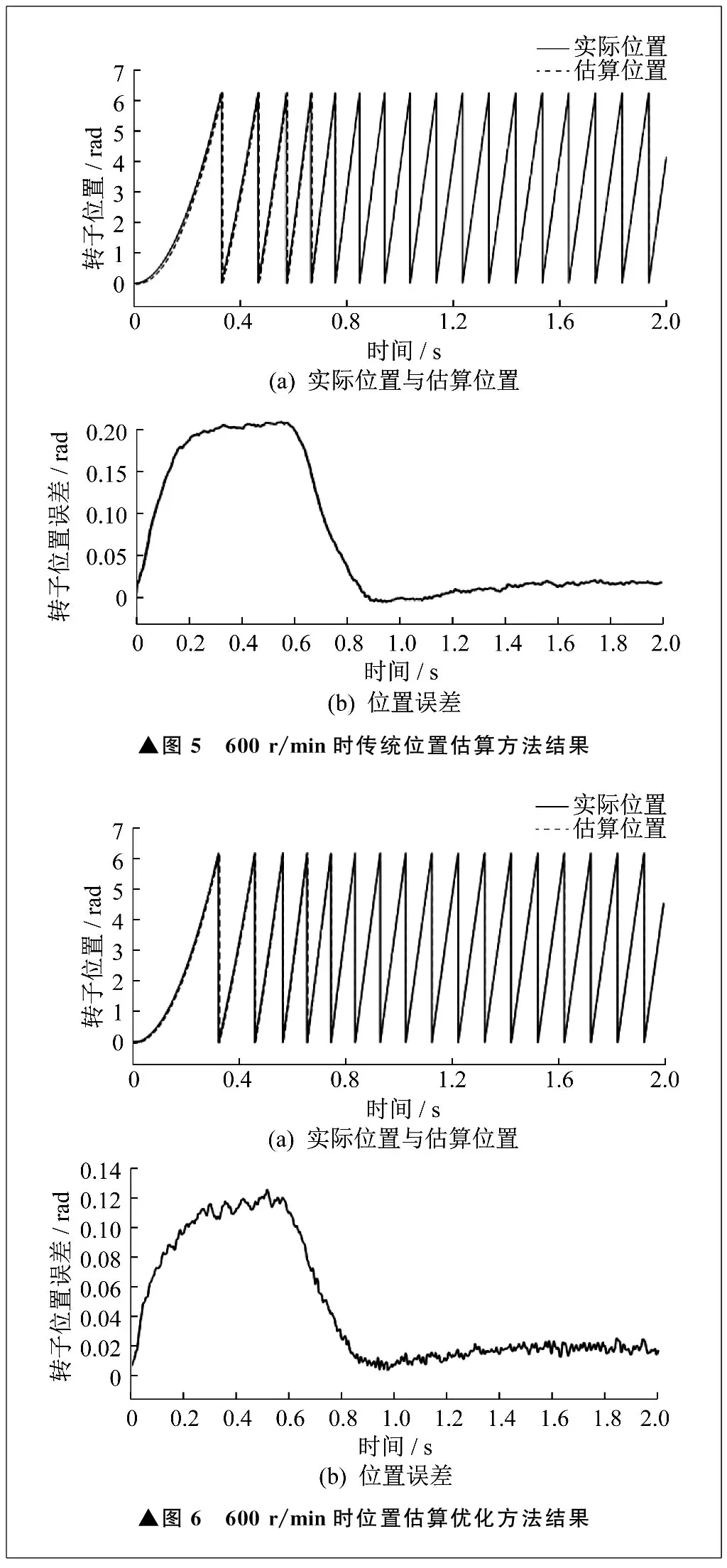
▲图5 600 r/min时传统位置估算方法结果▲图6 600 r/min时位置估算优化方法结果

6 试验验证

搭建基于STM32F401RET6单片机的试验平台,并选取符合试验需求的扇叶作为负载进行试验,同时保证试验所用的电机参数和设置与仿真相同。搭建的试验平台如图7所示。

▲图7 试验平台

传统位置估算方法及位置估算优化方法试验结果分别如图8、图9所示。对于传统位置估算方法,试验结果显示在0.8s时存在最大转子位置误差0.8 rad,在1.4s时达到稳态,此时转子位置误差为0.15 rad。相比之下,位置估算优化方法在0.7s时存在最大转子位置误差,仅为0.5 rad,在1.4 s时达到稳态,此时转子位置误差为0.1 rad。通过对比试验结果可知,位置估算优化方法具有更好的性能表现,能够显著减小最大转子位置误差,并提高系统稳态精度,与仿真结果相符,由此验证所提出方法的可行性。

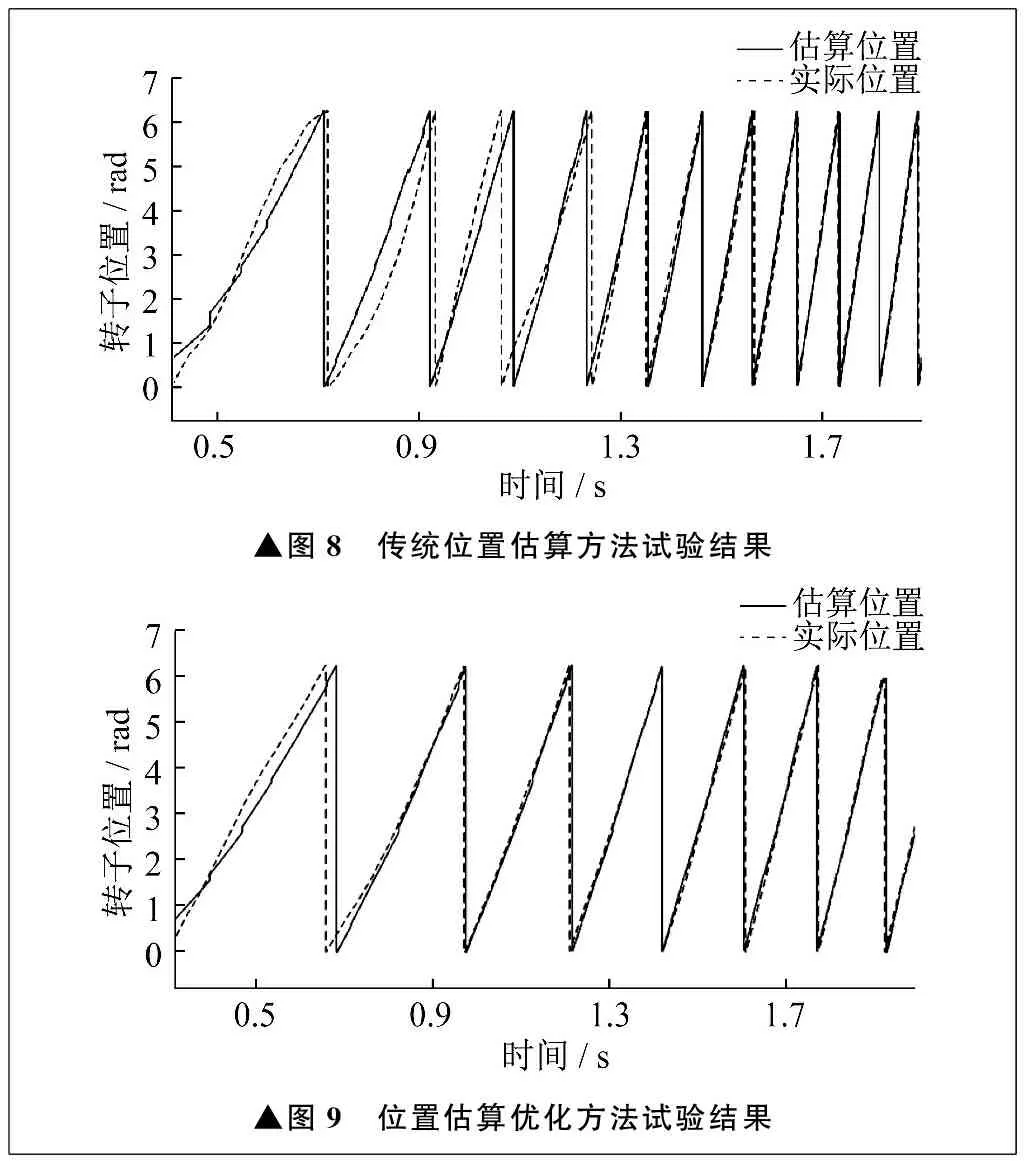
▲图8 传统位置估算方法试验结果▲图9 位置估算优化方法试验结果

7 结束语

笔者对基于脉振正弦波注入法的位置估算方法进行研究,为解决滤波器对系统动态性能影响的问题,提出了一种位置估算优化方法,使用两个广义二阶积分器代替传统位置估算环节中的带通滤波器和低通滤波器。仿真与试验结果表明,估算优化方法能够减小位置估算时的最大位置误差,改善系统的动态性能。