进气道可变高超声速飞行器自适应一体化控制

李家鑫,侯霖飞,李旦伟,吴国强

(1.大连理工大学, 辽宁 大连 116024; 2.沈阳飞机设计研究所, 沈阳 110035)

0 引言

吸气式高超声速飞行器(air-breathing hypersonic vehicle,AHSV)凭借可重复使用、大作战半径、宽速域等优点引起了世界军事大国的广泛关注。宽速域吸气式高超声速飞行器通常装备了冲压发动机,从而实现高超声速的优良推进性能[1-2]。由于高超声速飞行器机身前体作为进气道压缩面,后体具备尾喷管功能,这种一体化设计方法使高超声速飞行器飞行/推进耦合效应十分显著[3-4]。宽速域吸气式高超声速飞行器跨越亚声速、超声速、高超声速,飞行包线大,气动特性和推进特性变化显著。采用进气道变构型设计能够使飞行器在各个飞行任务段都具有满意的飞行效能,从而提升飞行器环境适应和生存能力,实现高品质跨域飞行[5]。因此,如何协调进气道结构变形与姿态稳定以确保进气道变形过程中的稳定可控是发展变体飞行器的关键技术。

国内外均对变进气道方案进行了广泛探索。美国“黑鸟”(SR-71)[6]采用了中心锥可移动的轴对称变几何进气道方案,其发动机通过平行移动锥形尖峰来满足不同飞行环境下所需要的气流量。Patrick等[7]对一种可整体伸缩的进气道压缩顶板进行研究,得到了气动性能随迎角变化等规律。宁啸天等[8]通过将平移唇罩安装于进气道外侧,通过移动平移唇罩的方式改变外压段激波与唇口的相对位置,从而使流量系数等指标达到设计要求。卢杰等[9]利用旋转低速唇罩和变压缩面的进气道结构,满足发动机在低速涡轮模态和高速冲压模态的工作需求,实现TBCC在2种模态之间的转换。刘雨等[10]对宽速域下的楔面压缩角可调二元进气道进行了数值仿真,证明几何构型可变进气道在高马赫数下的流量系数和总压恢复系数显著优于固定构型进气道。

此外,还有许多学者对高超声速飞行器一体化控制进行深入研究。Bu等[11]提出一种模糊最优控制策略解决动力学特性不确定的高超声速飞行器轨迹跟踪控制问题,并将一种模糊神经网络控制器应用于乘波飞行器,这种控制器结构简单,且能够保证令人满意的实时性能[12]。一种基于神经网络的非仿射控制器也被应用于高超声速飞行器,能够显著提升系统瞬态性能和稳态性能[13]。

前作对进气道可变的高超声速飞行器动力学特性和高超声速飞行器一体化控制分别进行研究,没有提出兼顾进气道结构变形与飞推耦合效应的耦合动力学特性分析方法和一体化控制方案。本文中利用高超声速动力学建模方法对飞行器进行高超声速气动和推进特性估算。研究了高超声速飞行器二元进气道3种构型参数下飞行器的气动和推进特性,分析了不同进气道构型参数对飞行器整体飞行力学和操稳特性的影响。此外,设计一种动力学参数依赖的一体化控制方法,在传统的攻角控制负反馈模型的基础上引入一条新的反馈通道,形成耦合反馈,该方法避免了复杂的飞行/推进系统解耦,相对于传统的单通道解耦控制显著提升系统动态性能。

1 进气道可变的高超声速飞行器建模方法

1.1 进气道可变的高超声速飞行器耦合动力学特性建模

动力学建模的目标是通过高超声速飞行器的气动性能建模和冲压热力循环建模实现对高超声速飞行器宽速域、大飞行包线内气动特性和推进特性的高可信度估算。

建模过程对高超声速飞行器外形进行部件拆分,通常分为机身部分、包括各控制翼面的机翼部分和发动机部分。各个部件的面元模型是实现飞行器高超声速气动特性估算的基础。其中,各控制翼面要能够根据计算输入要求进行偏转。模型发动机部分需要对进气道和尾喷管进行建模,这部分面元模型是对飞推耦合效应建模的关键。由于不同构型的高超声速飞行器进气道和尾喷管构型区别明显,因此这部分建模方法需要针对不同的构型特征灵活选取[14]。

在已有模型的基础上,相邻的4个采样点作为4个顶点可以构成一个四边形面元,以此类推,可以用四边形面元覆盖整个飞行器表面。对每个面元上的气动力进行估算并累加即可得到整机的气动力和力矩。面元高速气动特性估算方面,在迎风部分采用修正牛顿法,如式(1)与式(2)、非迎风面采用普朗特-梅耶法[15],如式(3)

Cp=Ksin2τ

(1)

(2)

(3)

其中:γe为比热比;τ为气流与面元的夹角。

在热力循环建模中,进气道采用激波膨胀波理论,计算每一个波面后的气流参数,当波系足够复杂时就计算此处的平均气流参数。隔离段燃烧室采用一维模型,忽略摩擦与燃烧速率,从守恒定理和能量增涨的角度计算燃料燃烧对气流参数的影响规律。在尾喷管采用羽流模型,根据自由流与高速膨胀气流压强相等处的剪切层计算压强[16]。

在面元与高速气动性能建模中,进气道尾喷管部分的面元受飞行姿态和推进系统的影响而表现出的气动特性与热力循环建模中,进气道在不同姿态下产生对空气的压缩效率的变化体现了高超声速飞行器的飞/推耦合特性[17]。

针对同一吸气式高超声速飞行器设计了3种不同的进气道构型。选取的高超声速飞行器有四阶压缩面,调整进气道构型时进气道压缩段起始点和终止点保持不变,每阶压缩面两端点相对于体轴位置不变,高度发生变化。所以进气道构型可以由前三阶压缩面的压缩角度确定。3种进气道构型示意图如图1,红线表示构型1;蓝线表示构型2;绿线表示构型3。进气道压缩面角度如表1所示。前三阶压缩面角度见表1所示。

图1 不同构型的进气道结构示意图

表1 进气道构型类型

1.2 考虑飞推耦合的高超声速飞行器动力学建模

对吸气式高超声速飞行器的纵向姿态控制通道进行设计。区别于传统飞行器纵向短周期运动微分方程,考虑飞推耦合的运动控制模型还加入了体现耦合效应的,对燃油当量比与俯仰力矩的描述。其中燃油当量比与速度、攻角、燃油当量比指令之间的物理关系非常复杂,用函数f表示。

(4)

式(4)中:ωZ为俯仰角速度;JZ为俯仰转动惯量;V为速度;θ为轨迹倾角;H为飞行高度;m为飞行器质量;ϑ为俯仰角;Pi、Yi分别为i型进气道构型下的推力、升力;g为重力加速度;α为攻角;φ为燃油当量比指令;φc为燃油当量比指令;Mzi、Mthi为i型进气道构型下的气动俯仰力矩和推进系统产生的俯仰力矩。

1.3 可变进气道构型下的耦合动力学特性分析与耦合状态空间模型

根据小扰动线性化理论,将高超声速飞行器在纵向运动平衡状态点上展开。飞/推耦合模型与传统模型的区别在于考虑了攻角对推进特性的影响和燃油当量比对升力、阻力、俯仰力矩等气动特性的影响,短周期小扰动动力学方程如下:

(5)

(6)

(7)

a33=gsinθ/V表示重力加速度引起弹道斜线方向的转动角速度偏量,和进气道构型无关。

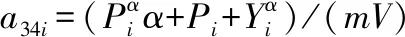
(8)

(9)

a41i和a44i为i型进气道构型下速度和攻角引起的燃油当量比变化偏量;dM为发动机空气质量流率。

a47=Kωn表示当前飞行条件下,燃油当量比指令引起的燃油当量比变化偏量,表现为燃油当量比指令到实际燃油当量比的滞后,与进气道构型无关。

针对纵向短周期扰动运动的状态空间标准表达形式为

(10)

(11)

系统有2个控制量,分别是升降舵和燃油当量比指令;状态量分别是燃油当量比,角速度、俯仰角、攻角。该系统是耦合多入多出系统。

2 进气道可变的高超声速动力学与操稳分析

2.1 考虑进气道可变的高超声速飞行器飞行力学分析

根据第二章所述动力学建模方法。对3种不同进气道构型的高超声速飞行器建模,分析结果如图2所示。

图2 不同构型进气道对飞行力学特性的影响

图2说明进气道压缩面的构型1设计相对于其他2种构型明显降低了升阻比,但是在小迎角状态增大了推力,且空气质量流率的变化是导致推力系数变化的主要原因。合理设计进气道构型能够使空气质量流率达到最大,从而使推力达到最大值,这个转折角是能够让进气道达到激波封口状态的转折角。比冲与空气质量流率保持相同的变化规律,且比冲更大的进气道构型能够使高超声速飞行器具备更好的轨迹性能。

2.2 考虑可变进气道的飞推耦合动力学与操稳特性分析

对不同的进气道构型静稳定性a24和静操纵性a25进行分析,结果如图3所示。此外,在状态空间模型中的状态矩阵在变进气道的过程中会发生变化。由定义可知,a22、a33、a47在变进气道过程中保持不变。因此对状态空间矩阵中的其他元素进行分析。

图3 变进气道动力学特性分析

结果表明,除a22、a33、a47外,还有a25静操纵性和a35不受进气道构型变化的影响;相对应的a24静稳定性、a34、a36、a44等与飞推耦合效应相关的指标在进气道变构型过程中变化明显。这说明进气道构型能够显著影响飞行器飞推耦合的程度,同时给飞行控制带来困难。

3 变进气道一体化飞行控制设计

上文已经阐明高超声速飞行器显著的飞行/推进耦合特性,所以在飞行控制设计阶段把高超声速飞行器视为多入多出系统。假设高超声速飞行器在高空高速变进气道过程中,飞行力学性能参数均匀变化。通过极点配置实现耦合反馈控制,控制流程包括根据期望超调量和调节时间选择期望极点位置、控制器参数求解、控制分配,最后,通过调整控制器参数保证高超声速飞行器在变进气道的过程中系统期望极点位置不变,以取得比解耦控制更好的控制效果。

根据升降舵控制攻角和燃料当量比指令控制燃油当量比的逻辑,将状态空间方程构建的四阶系统分解为三阶系统和一阶系统,对应攻角控制系统和燃油当量比控制系统。通常认为三阶系统具有2个主导极点和一个非主导极点,系统动态指标由2个主导极点决定;主导极点的位置与其对应系统的性能指标有明确对应关系,可以通过计算阻尼比和固有频率,然后选择主导极点。其表达式为

(12)

(13)

其中:λ1,2为2个主导极点;ξ为系统阻尼比;ωn为系统自然频率;ts为调节时间;σ为系统超调量。

完成了2个主导极点的选择后,可以根据主导极点的实部,自主选择第3个极点即非主导极点,通常选主导极点的5倍以上的值作为非主导极点,即:λ3=-nξωn

n为选定的倍数,这个倍数可以通过实际控制效果进行调整。

一阶系统有一个极点,记为:λ4=-1/T

其中T为一阶系统时间常数,一阶系统调节时间通常为4T,所以可以通过理想的调节时间选定一阶系统的极点。

至此,4个期望极点的位置可以全部确定。控制器可以表示为:

U=Uc-KΔX

(14)

其中,Uc为配平状态下的控制输入。在控制矩阵K解算方面,可以采用变换矩阵法。

(15)

式(15)中,ai为A矩阵特征多项式的系数。耦合负反馈控制系统A-BK在选定目标极点上的特征方程为

(s-λ1)(s-λ2)(s-λ3)(s-λ4)=

s4+α1s3+α2s2+α3s+α4

(16)

则控制矩阵K可以写为

(17)

如图4所示,当吸气式高超声速飞行器在宽速域飞行,且气动参数发生显著变化。通过调整控制矩阵K,保证A+BK矩阵元素值在进气道构型和气动环境均发生变化的情况下保持不变。

图4 增益更新迭代流程

控制矩阵K为2行4列矩阵,第1行对控制量δz升降舵偏角进行计算;第2行对控制量φc燃油当量比指令进行计算。2个控制量都由燃油当量比、角速度、俯仰角、攻角4个物理量的偏差共同决定。相对于传统解耦控制,即通过攻角偏差计算升降舵偏角;速度偏差计算燃油当量比,实现了一体化的耦合反馈控制。

仿真初始条件的设定如表2所示。仿真结果包括正常工况下的动态响应过程、添加20%不确定性后的升降舵动态响应过程以及添加20%不确定性时控制器自适应补偿的动态响应过程。模拟结果如图5所示。

图5 升力±20%拉偏迎角和升降舵变化对比

表2 初始仿真条件设置

由图5可以看出,无拉偏标准情况下,PID控制对迎角的超调量为27.8%,调节时间(按5%计算)为:3.85 s。与之相比,自适应一体化控制的最大超调量和调节时间大幅减小,最大超调量为4.85%,调节时间为1.22 s。从图6可以看出一体化控制对最大超调量的抑制效果更好。同时,在整个调节过程中,一体化控制下的系统状态更接近于稳态,这也为执行机构留出更大的操纵裕度。除俯仰角外,2种控制方法对升力±20%拉偏并不敏感,与标准情况下基本相同,且一体化控制的效果总是优于传统的PID控制。

图6 升力±20%拉偏俯仰角速度/俯仰角变化对比

4 结论

针对变几何进气道带来飞行器动力学特性变化及飞推耦合问题进行了以下的研究并且得到相关结论:

1) 对飞行器进行了动力学建模和气动、推进特性的估算,得到了高超声速飞行器的大飞行包线、宽速域的动力学特性。对比分析了3种不同进气道构型参数下高超声速飞行器的飞行力学特性,结果显示进气道构型对俯仰力矩和升力都有明显的影响,且能够通过影响空气质量流率进而显著改变推力和比冲。

2) 对考虑进气道可变的吸气式高超声速飞行器的耦合操稳特性和动力学特征参数进行分析。在变进气道过程中,静稳定性和与飞推耦合效应相关的指标均发生变化。而操纵性等指标不发生变化。

3) 设计了动力学参数依赖的自适应一体化控制器,实现了耦合反馈控制。对升力拉偏±20%的情况下对2种控制方式的效果进行比较,结果表明自适应一体化相较于传统的PID控制能够明显降低超调量和调节时间。