基于多压力变温实验的缸套-活塞环摩擦因数预测研究*

马 轩 王 哲 刘晓日

(1.河北工业大学能源与环境工程学院 天津 300401；2.清华大学天津高端装备研究院 天津 300300)

在内燃机的摩擦损失中，仅活塞环-缸套摩擦副所产生的摩擦损失即可占20%～30%[1]，是内燃机最主要的一项机械损失。随气缸内的燃烧以及活塞环和缸套的运动摩擦过程，活塞环接触范围内缸套的温差能达到50 ℃以上的高温跨度[2-3]，且随活塞沿气缸轴向从上止点至下止点的工作过程，在温度变化的同时也伴随着快速的压力变化。因此整合内燃机工作过程中温度、压力及润滑油性能参数变化，建立缸套-活塞环摩擦因数预测模型，对于降低该摩擦副的摩擦损失具有重要意义。

已有研究表明，在缸套-活塞环摩擦副中，缸套的温度对活塞环摩擦功耗的影响较为显著。基于润滑油温度等于缸套温度且为定值的假设，WOLFF[4]和RAHMANI等[5]分别在实验中设定不同的缸套温度，研究了温度对活塞环摩擦功耗的影响，结果表明缸套或润滑油温度偏低时活塞环流体摩擦功耗较显著，而高温时流体摩擦功耗降低，粗糙接触摩擦功耗显著增加。同时，相关研究也表明，摩擦热量会造成润滑油黏度和密度降低[6-7]，并且在摩擦过程中油膜厚度随温度升高而减小，使得微凸峰接触数量增多，局部温升增大，从而加剧摩擦功耗[8]。

目前内燃机缸套-活塞环系统的摩擦磨损改良，主要从润滑油性能、表面改性、动力学特性等方面展开[9]。而缸套-活塞环摩擦副在摩擦过程中存在多种物质的相互作用，包含实际工况的温度、压力以及摩擦表面的纹理与涂层处理[10-11]和润滑油黏度、添加剂作用[12]等，在众多条件的影响下，很难以线性的数学方法描述该摩擦副的摩擦性能与各种影响因素之间的作用关系。所以本文作者拟通过实验的方法模拟内燃机工况，采集摩擦性能数据并构建神经网络模型对数据进行训练以实现摩擦因数的预测。

BP(Back Propagation)神经网络是一种多层前馈式神经网络模型[13]，通过信号前向计算和误差反向传播修正以及储存大量无需事先描述的输入-输出映射关系，具有良好的线性和非线性映射能力，目前在多因素复杂系统的预测问题上已取得了良好的效果。NIU等[14]整合跑道表面状况和轮胎状况提出了一种移动式天气-跑道-轮胎的传感器系统来估计摩擦因数，将神经网络的输出(估计摩擦因数)与相关模型相关联，以预测飞机刹车时轮胎与跑道之间的摩擦因数。RIBEIRO等[15]采用时延神经网络(TDNN)检测横向力激励下的道路摩擦因数，并基于真实车辆模型进行了验证。TODOROVIC等[16]提出了一种基于神经网络的四驱车摩擦势预测模型，可以同时预测纵向和横向激励下的摩擦势。在神经网络方法和摩擦属性的结合上，目前已取得了较好的成果，但是将神经网络方法应用在内燃机缸套-活塞环摩擦副上，预测摩擦因数和接触面温度、载荷等因素的关系和摩擦因数变化趋势，相关研究尚不多见。

本文作者以内燃机系统的缸套-活塞环的摩擦因数为输出参数，摩擦接触温度、接触压力以及润滑油黏度为输入参数，构建BP神经网络预测模型。对比实验结果和模型预测结果，验证了所构建的神经网络预测模型可以准确地预测缸套-活塞环的摩擦因数，为内燃机摩擦性能预测及改进提供了新的思路。

1 实验部分

1.1 实验材料及实验装置

内燃机系统中，缸套与第一道活塞环之间的摩擦工况最为恶劣，所以摩擦副材料采用原厂生产的某型号柴油机的缸套以及对应的第一道活塞环，并切割成实验所需尺寸。润滑油选择重型柴油机常用的15W-40润滑油。

采用SRV高温摩擦磨损试验机(见图1)可对多种摩擦副进行实验，输出的摩擦因数曲线能够直观反映出摩擦副及润滑油的摩擦学性能[17]。文中通过SRV高温摩擦磨损试验机模拟缸套-活塞环摩擦副之间的往复式运动。

1.2 实验条件

根据该型柴油机在实际工作中的额定工况参数设置实验条件。在柴油机的实际工况中，当活塞达到上止点后曲轴转角为9°时，缸套-活塞环摩擦副达到最大接触压力16.82 MPa，此时接触温度达到190 ℃。基于以上条件，在300～1 500 N压力区间内设置5组定压变温实验(见表1)，其中设置1 220 N对应16.82 MPa的上止点工况载荷。

如表2所示，变温实验设置初始温度为室温，在初期磨合过程中逐渐施加载荷至指定值，并稳定温度为30 ℃，然后利用加热模组开始均匀加热，使摩擦试件的温度由初始温度按4.25 ℃/min速率均匀变化至200 ℃。实验中设置温度加热上限为200 ℃，作为模型构建的输入参数时仅取到190 ℃，主要因为在测试润滑油黏度随温度的变化时，由于实验设备限制，温度上限难以达到200 ℃的要求。通过实验测试了不同预设压力下摩擦因数随于温度的变化，以及15W-40润滑油在0～190 ℃之间的黏度变化曲线。

表2 实验基本参数

1.3 实验数据

图2展示了不同载荷下摩擦因数随温度(20～190 ℃)的变化关系。可以看出，载荷为4.14 MPa时，摩擦因数整体在0.14～0.15之间波动，呈现出较为稳定的趋势，主要原因在于载荷较小，摩擦副之间的粗糙峰接触较少，此时的摩擦状态为油膜流体摩擦，其摩擦因数主要由润滑油性质决定；载荷为8.27 MPa时，摩擦因数曲线随温度增加呈现出先升后降的趋势，且在95 ℃时摩擦因数达到最大值0.163；当载荷为12.41、16.82、20.48 MPa时，摩擦因数曲线变化规律比较接近，均在65～75 ℃温度区间摩擦因数达到最大值，且最大值稳定在0.156，然后随温度进一步升高，摩擦因数值由上升趋势转变为下降。以16.82 MPa工况实验为例，润滑油黏度由30 ℃时的0.233 5 Pa·s降低至99 ℃时的0.014 6 Pa·s，此时黏度已达到一较低值，油膜黏度的变化对摩擦因数影响较小，粗糙峰接触情况渐趋稳定；同时，润滑油中所含的极压添加剂在较高温度和载荷下，与金属反应并在粗糙峰表面生成剪切应力较低的化学反应膜，从而减少粗糙峰的直接接触[18]；并且随着摩擦温度上升，粗糙峰位置的局部温度较高，金属塑性增强、材料软化且出现一定的氧化现象[19]，这些现象的产生起到了一定的减摩作用，从而导致摩擦因数降低。

载荷变化对摩擦工况的影响较为复杂。对于一般情况下的滑动摩擦，载荷增大时，摩擦阻力增大，而同时伴随着微凸体接触增加，即摩擦接触面积增大。活塞环和缸套组成的摩擦副主要为弹性材料，其摩擦接触面积S与摩擦副间的压力Fn的2/3次方成正比[20]。并且在摩擦过程中，载荷增加使得接触面积增加，进而产生较大的塑性应力和剪切力，并产生大量摩擦热，摩擦反应膜的形成最终导致摩擦因数进一步降低。因而在随着载荷增加时，摩擦因数的峰值最大为8.27 MPa工况的0.162 6，而随着载荷继续增加，其峰值降低，见表3。

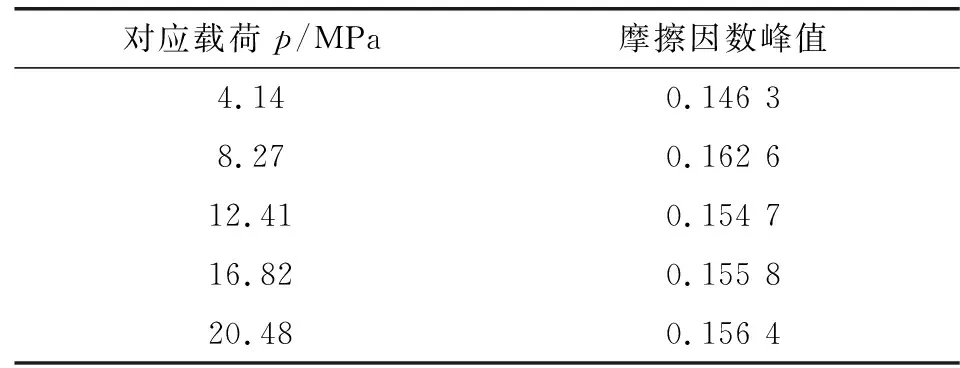
表3 不同载荷下的摩擦因数峰值

图3展示了润滑油黏度随温度的变化关系。可见，润滑油黏度在30～80 ℃温度区间内呈现快速降低的趋势，当温度高于100 ℃后，黏度降速趋缓，最终趋近于0.003 Pa·s。在摩擦过程中，机油黏度的影响区间主要在80 ℃以内。

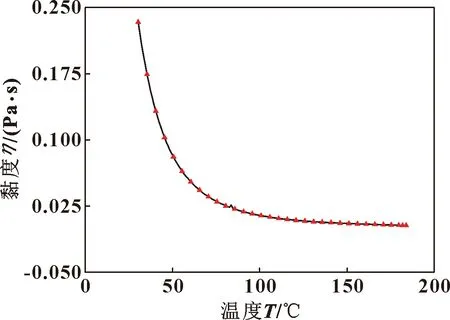
图3 润滑油黏度随接触面温度的变化

2 BP神经网络预测模型

如图4所示，Back Propagation(BP)神经网络由输入层、隐含层和输出层构成，输入层设置摩擦接触温度、接触载荷、润滑油黏度3个输入单元；隐含层神经元数目通常由经验和测试确定，模型设置3个输入单元，所以隐含层神经元数量设置为9个；输出层为对应输入参数下的缸套-活塞环摩擦因数。

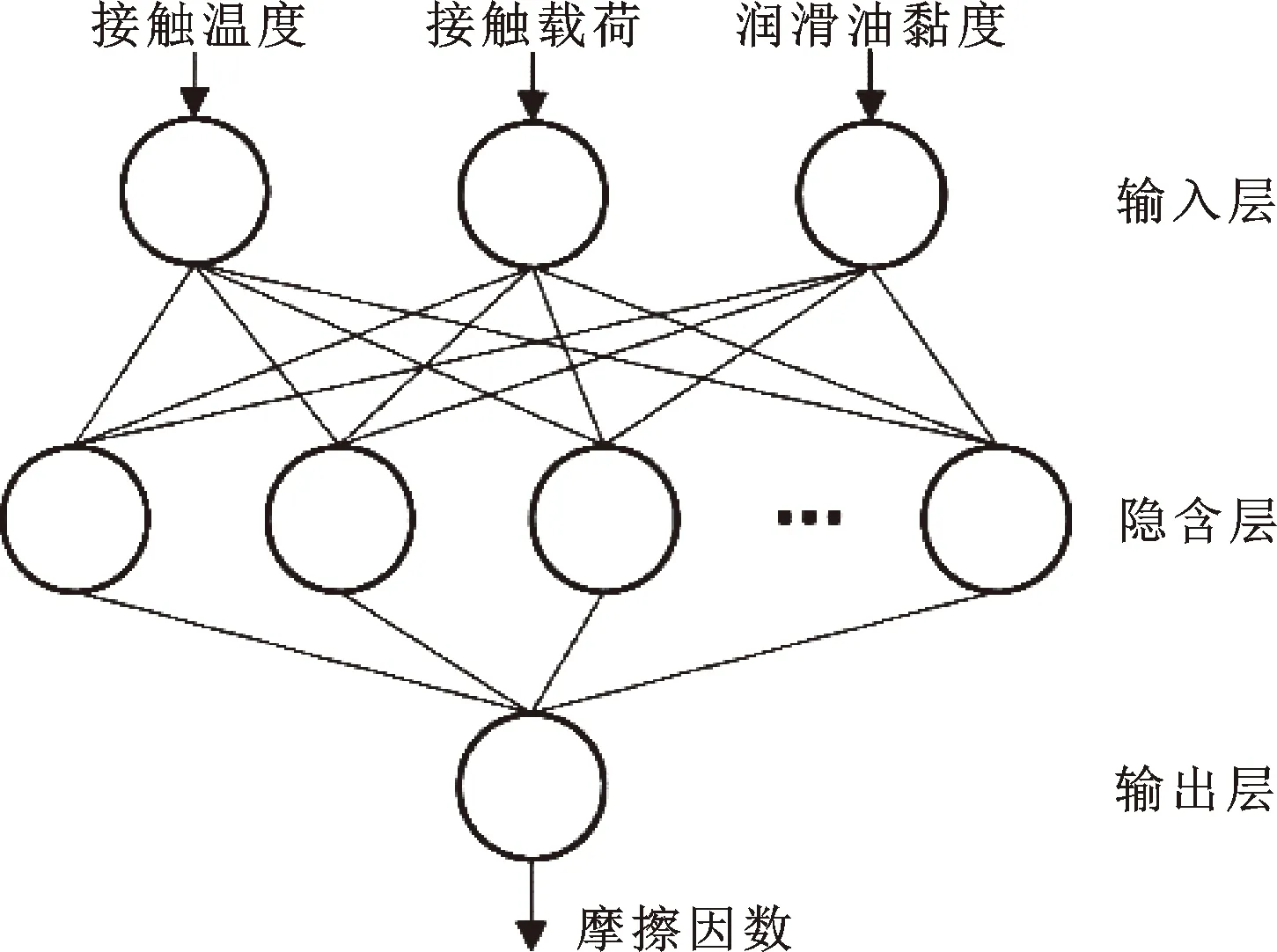
图4 BP神经网络结构

2.1 输入值预处理

实验数据在导入模型前进行归一化，既可消除量纲的影响，也能够提高模型的训练速度。当某个输入参数在某一区间内呈现跨数量级的变化时，则在这一区间内其对输出参数的影响权重较大，预处理时进行归一化可有效提高模型训练的性能。将数据进行归一化处理的常用公式如下：

(1)

式中：Xi为变换后的变量；xi为输入或输出变量的原始数据；xmin为输入数据中的最小值；xmax为输入数据中的最大值。

经归一化处理后，输入参数的原始数据由[xmin，xmax]变为[0，1]。

在实验数据中，从30～190 ℃温度区间内共提取出1 280组数据，其中70%作为训练集，15%作交叉检验集，15%作为测试集。

2.2 训练算法的选择

神经网络模型中的训练算法及传递函数采用Matlab软件的Neural Network工具箱中的相关函数。输入层和隐含层传递函数选用tansig函数，输出层选用线性的purelin函数，训练算法拟采用梯度下降算法(traingd 函数)和L-M算法(trainlm 函数)，通过比较训练过程中2种算法的误差下降速率来确定模型最终应用的训练算法。

L-M算法类似于拟牛顿算法，主要根据下式修正网络权值：

ωn+1=ωn-[JTJ+μJ]-1JTe

(2)

式中：ωn和ωn+1分别为修正前后的网络权值；J是包含误差性能函数对网络权值一阶导数的雅克比矩阵。

当μ=0时，L-M算法退化为拟牛顿法；当μ值较大时，式(2)相当于补偿较小的梯度下降法。

图5展示了2种算法在相同训练集参数下的误差下降速度。采用梯度下降算法，经过1 000次迭代，误差尚未达到所设置的收敛精度；而L-M算法仅在43次计算之后即达到收敛精度。所以在模型中选用L-M算法作为实际应用的训练算法。经过以上分析，确定模型所选用算法如表4所示。

表4 预测模型的结构参数

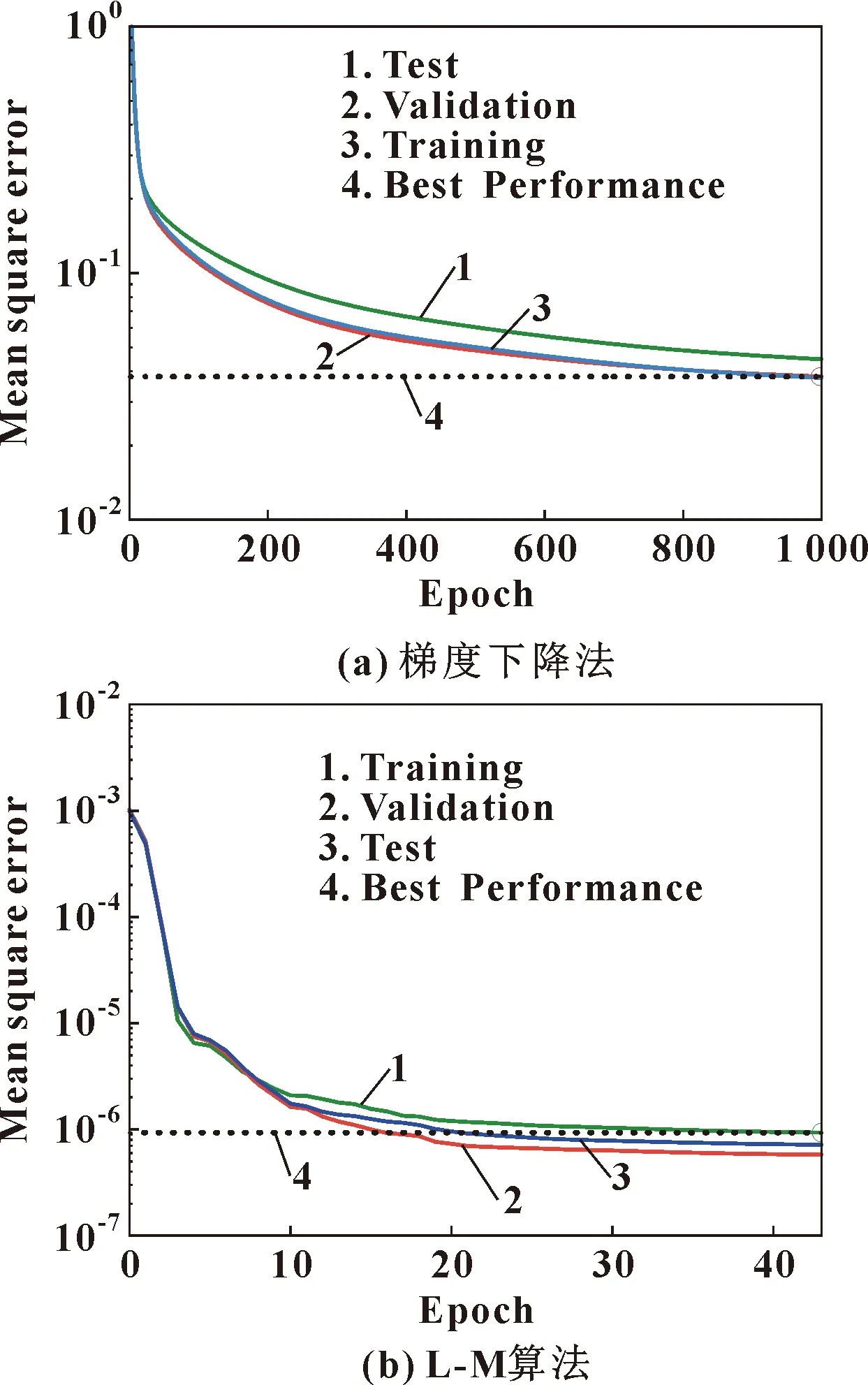
图5 训练算法的误差收敛性

2.3 模型预测与分析

经过43次迭代训练，模型达到所设置的误差收敛精度。运行用时0.42 s，计算均方误差MSE为9.331×10-7，表明所构建BP神经网络模型具有较好的泛化效果。

图6展示了在训练过程中所获得的R回归值。R值表示预测值和设定值的关系度，当R值接近1时，表示预测值与设定参数具有较高的相关性。从图中看，在训练集(Training)、交叉检验集(Validation)以及测试集(Test)所有数据点的综合回归分析中，R回归值达到0.996 26，表明在训练与预测过程中，模型对各参数具有较高的处理能力。

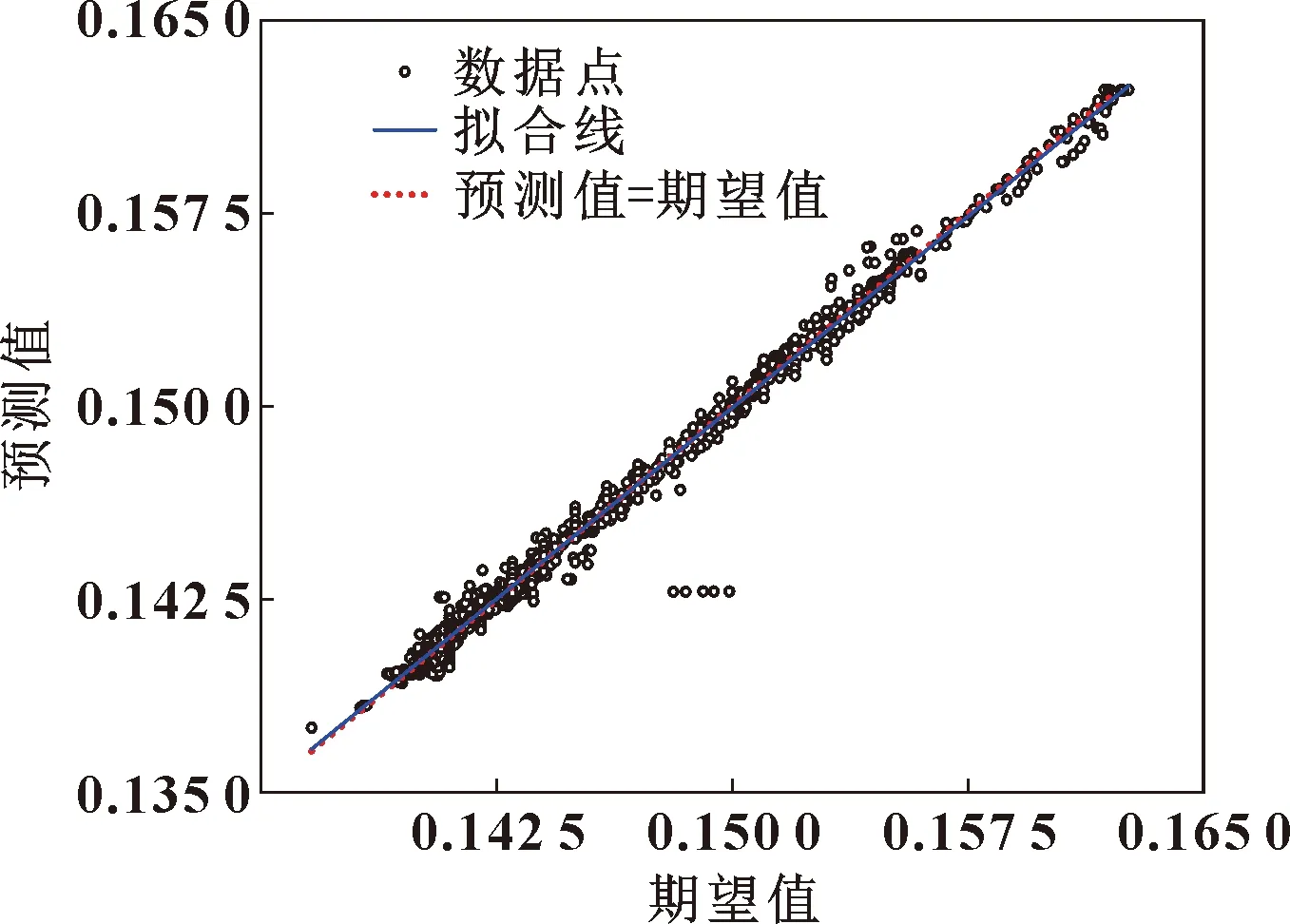
图6 预测模型回归分析

图7展示了测试集的5组数据预测值和期望值的关系。测试集参数分别在5组不同载荷的实验结果中按每5 ℃取点，共180个采集点。从图中不难看出，预测值与期望值的数据分布基本相同，该模型对摩擦因数的变化趋势具有较好的预测性能。对5组数据的预测趋势均和实验期望值的分布相符，均呈现出随温度增大而先升后降的趋势。在输入温度大于150 ℃后，实验测得的摩擦因数呈现出波动上升的趋势，而在该温度区间内，预测值分布呈现为一段较为稳定的曲线。综合图8中展示的误差分布，结果表明在这一区间内，相比较实验测定所存在的偶然性导致的摩擦因数波动，BP神经网络模型可在保证误差值的条件下做出较为稳定的预测过程。

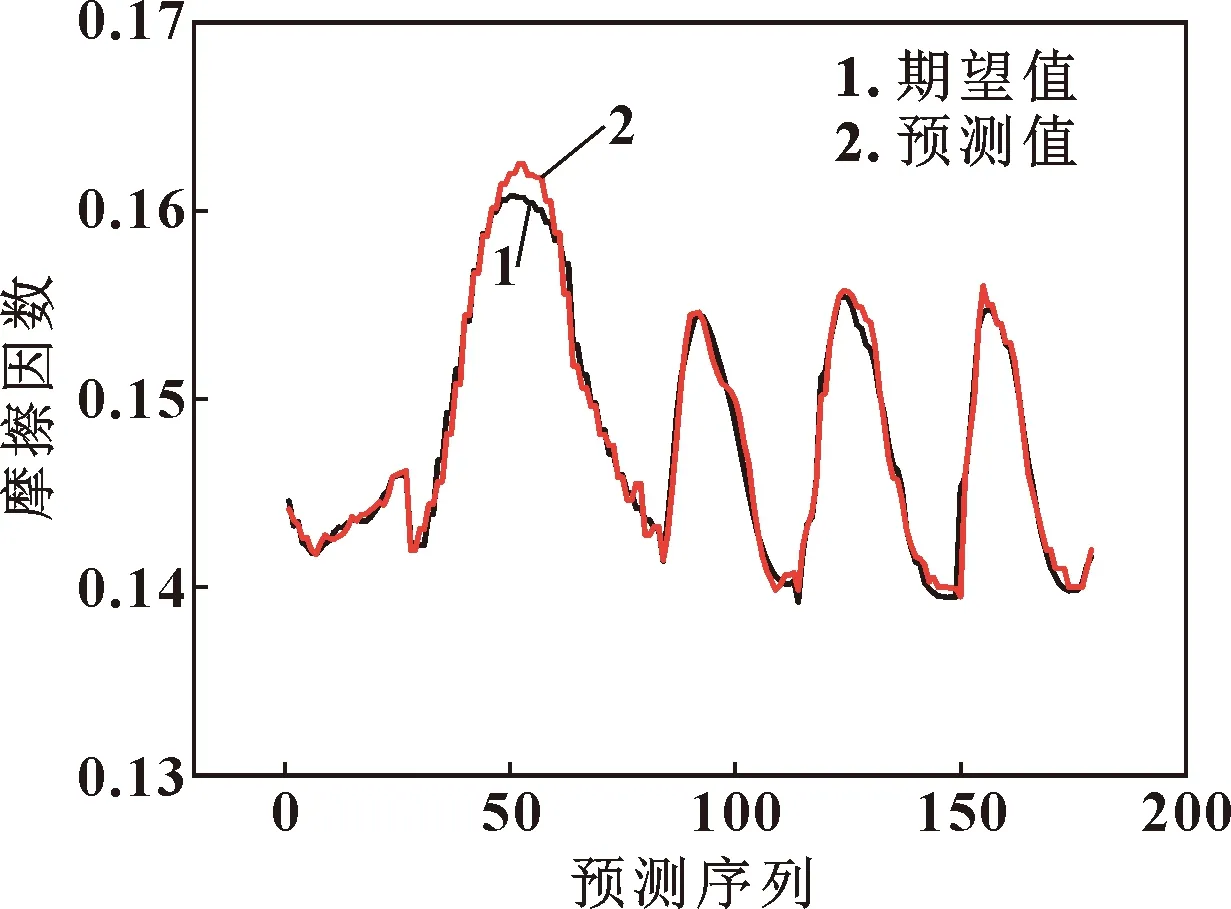
图7 预测值与期望值对比

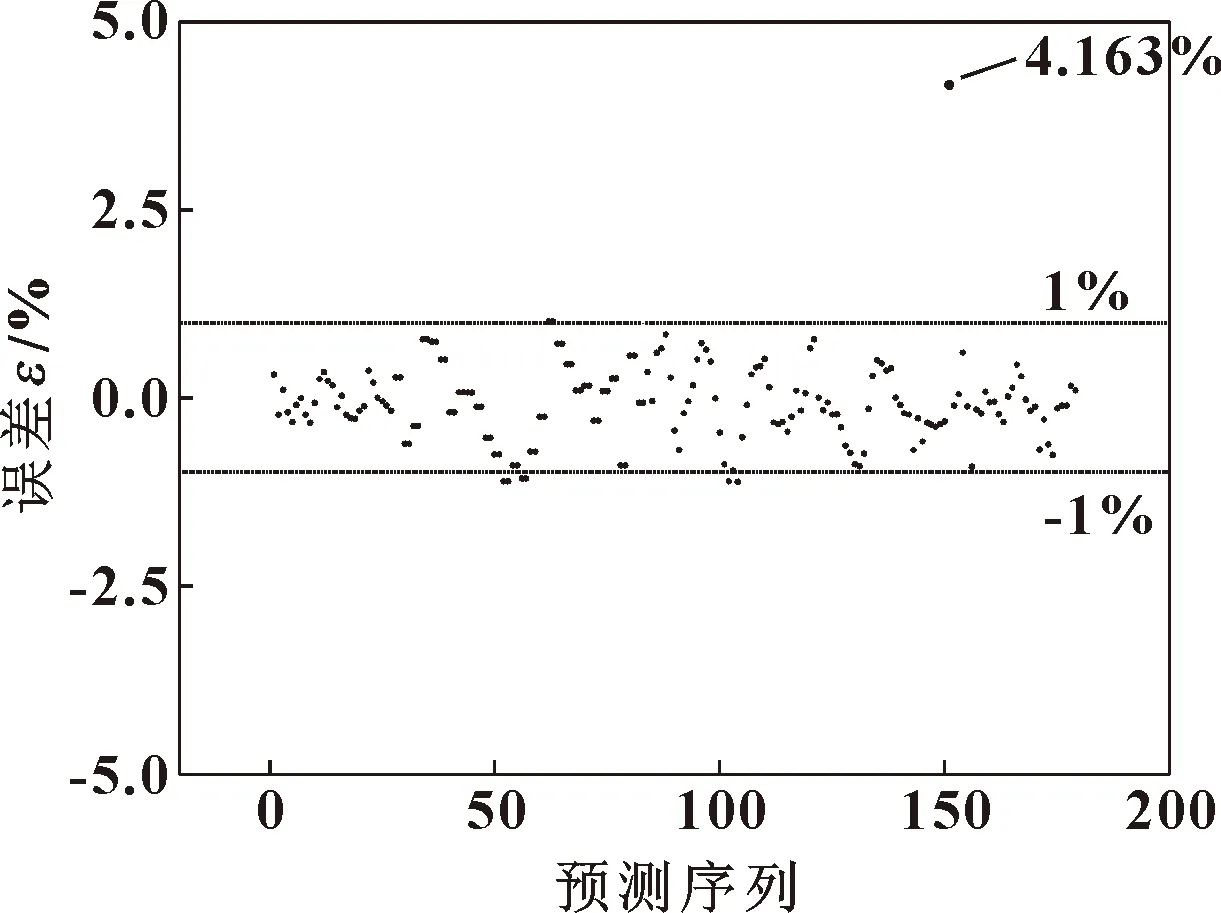
图8 预测误差分析

图8中显示出测试集中180组样本数据的误差分布，误差值基本小于1%。在所有的误差数据中，最大误差为4.163%，最小为0.000 4%，误差小于1%的数据共171组，除最大误差外，预测结果较为精准，基本满足工程精度要求。

2.4 模型预测应用

在30～190 ℃的温度区间内每隔0.5 ℃取点，在4.13～20.68 MPa的载荷区间内每隔0.138 MPa(对应实验压力变化为10 N)取点，获得321×121组数据，并根据温度取点，在黏度实验输出的黏温曲线中取出对应温度的黏度值。以接触面温度、载荷、黏度为输入，利用训练好的神经网络模型进行预测，输出一组321×121的关于接触面温度和载荷的摩擦因数预测值散点矩阵。

图9所示为不同载荷和温度下摩擦因数预测值散点矩阵的三维曲面。可以看出，沿载荷增加方向，摩擦因数呈现出先下降后稳定的趋势。当载荷较小时，摩擦副的摩擦状态为油膜流体摩擦，所以在30～190 ℃的温度区间内摩擦因数在0.145附近波动。随载荷逐渐增大，微凸体接触加剧，摩擦接触面逐渐进入混合摩擦状态，载荷对摩擦因数的影响增大。接触面温度低于100 ℃时，在同一温度下，摩擦因数随着载荷的初步上升而增大，然后在0.150～0.155的区间内趋于稳定。沿温度增加方向，除在4 MPa附近的低载荷区间摩擦因数呈现较为稳定的状态，在其余的载荷区间内，摩擦因数的预测值随温度增加均表现出先升后降的趋势。图9中摩擦因数整体预测结果与实验结果较为吻合。

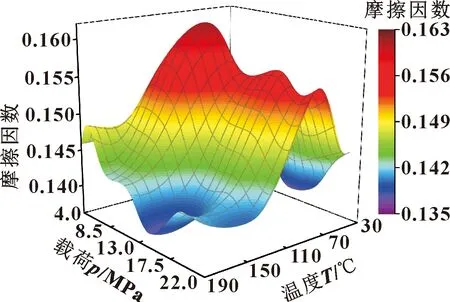
图9 不同载荷和温度下摩擦因数预测曲面

利用神经网络对实验数据进行训练仅需较少的时间，当模型完成训练后，输入参数可以即时完成预测参数的输出，有效降低了计算成本。且机器学习方式的预测结果明显优于经验公式或半经验公式计算结果。因此，针对缸套-活塞环摩擦副实际工况的复杂过程，BP预测模型可有效解决在温度、载荷、摩擦产热以及润滑油性质等多因素作用下确定摩擦因数的问题，在内燃机摩擦副摩擦性能预测方面具有广阔的应用前景，也为该领域的进一步研究提供了新的方法和思路。

3 结论

通过对缸套-活塞环摩擦副在不同定压力下进行变温实验，并构建BP神经网络模型以接触面温度、载荷、润滑油黏度作为输入，预测了对应的摩擦因数。得出主要结论如下：

(1)当缸套-活塞环摩擦副的接触面载荷较低，处于4 MPa附近时，接触面接近油膜流体摩擦状态，其摩擦因数较低，此时温度变化以及伴随的润滑油黏度变化对摩擦因数的影响较小。当摩擦副接触面载荷上升至8 MPa，微凸体接触加剧，随着载荷进一步增加，摩擦因数的变化趋于稳定。

(2)载荷大于8 MPa的摩擦因数曲线均表现出在温度升高初期摩擦因数明显增加的趋势，主要原因为15W-40型润滑油的黏度在温度从室温升高至80 ℃过程中迅速降低，对摩擦性能的影响较大。当温度逐渐升高至100 ℃后，此时黏性摩擦不再起到主导作用，润滑油中所含有的极压添加剂在粗糙峰表面形成了化学反应膜，起到了减摩和润滑效果，使得摩擦因数随温度升高呈现出下降趋势。

(3)以接触面温度、载荷以及润滑油黏度作为输入参数，摩擦因数作为输出参数构建的BP神经网络，在经过训练后表现出良好的预测精度，误差基本保持在1%以内，且关于接触面温度、载荷的摩擦因数曲面预测结果与实验结果较为吻合，为内燃机摩擦性能预测提供了新思路。