挂式空调贯流风机CFD 降维计算可靠性研究
王晓春 徐萌 苏钊 丁爽 龚慧峰 吴涛
(1.青岛海尔智能技术研发有限公司,山东青岛 266101;2.数字化家电国家重点实验室,山东青岛 266101;3.海尔智家股份有限公司,山东青岛 266101;4.青岛海尔空调器有限总公司,山东青岛 266101)
挂机空调室内机送风叶轮为贯流风机,其特点为沿着轴线方向送风相对均匀、噪声低、结构紧凑。贯流风机理论并不复杂,但由于其结构的独特性及高转速特性,导致使用CFD 研究三维计算规模较大[1]。
对于制冷系统仿真而言,有效地获取截面的风量分配是获取换热量、制冷剂压降计算的关键因素之一,如何快速有效地获取表面风量分布决定着制冷系统仿真应用的效率。已有的研究中大多探索了三维贯流风机或者二维贯流风机流动特性[2,3],通过仿真结合试验的方法[4]研究风机叶片优化对风量、噪声的影响因素[5,6],并没有阐述三维模型及二维模型计算的差异性。
本文在前人仿真试验对标模型的基础上,利用焓差室风量测试数据做依据,分析了不同转速等条件下,总风量仿真的可靠性及三维和简化二维模型总风量、风量分布情况的可行性,为以二维风量分配计算在制冷系统仿真业务开展提供了依据。
1 仿真模型建立及可靠性验证
1.1 仿真模型
为了确保仿真与试验的一致性,在三维模型中,保留了完整的叶轮结构、进风格栅、出风导叶片等。翅片采用多孔介质模型替代,其惯性阻力系数和粘性阻力系数由风洞实验室测试数据(如表1 所示)处理得到惯性阻力系数为116 kg/m4,粘性阻力系数314 kg/m3·s。
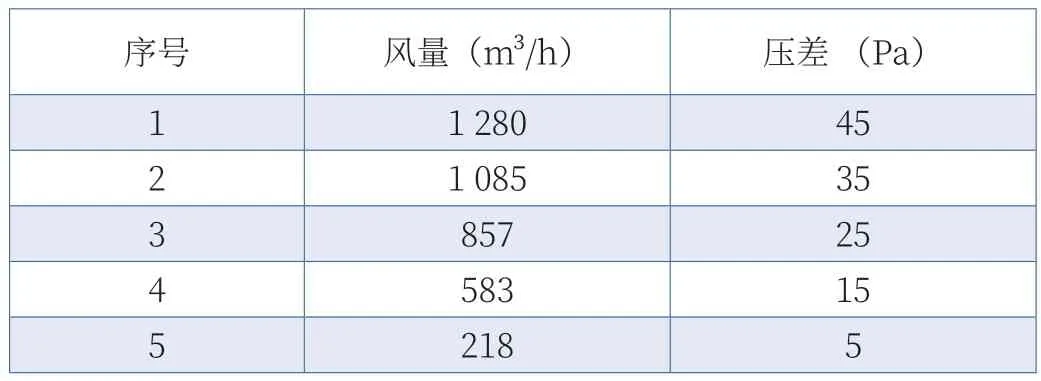
表1 风洞P-Q 测试数据
湍流模型采用k-e,标准壁面函数,非定常仿真动静交界面采用Motion 网格技术处理,时间步长设定为1e-05 秒。为了捕捉到光滑的叶轮表面信息,研究了表面网格控制尺度在0.15 mm~0.5 mm,各尺度下叶轮表面网格形态如图1,模型选择0.15 mm 作为最小表面网格尺寸。

图1 不同尺度表面网格对叶片表面光滑度影响
1.2 网格无关性验证及精度确保
本文以高频转速1 300 rpm、非定常三维仿真开展网格无关性研究,受限于计算资源及效率,探索了5 种网格数量的流量计算值差异,图2 为不同网格尺度下的计算结果,采用6 130 万网格与试验值834 m3/h 相比,误差为2.73%,模型处于较高精度,验证了计算结果的可靠性。

图2 网格无关性研究
后续以此网格配置为基础开展相关研究。图3 为该网格尺度下叶轮的Y+分布情况。

图3 Y+分布
2 结果对比分析及应用
2.1 三维仿真不同转速可靠性分析
基于上述三维非定常模型及多孔介质模型,计算了900 rpm、1 300 rpm、1 606 rpm 三种转速下的总风量、蒸发器表面风量分配情况,表2 为相应的仿真与试验统计信息,整体偏差在8%以内,判定仿真计算有效。
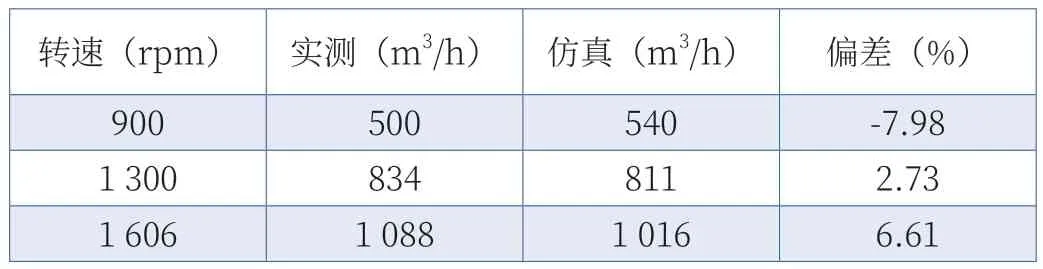
表2 不同转速三维瞬态仿真试验对比
本文研究的目的是论证服务于制冷系统仿真的换热器表面分配用二维替代三维进行CFD计算的可靠性,为达成这一目标,将换热器表面按照图4 虚切线的形式将换热器进风侧拆分为17段,叶轮展向作为一整段取数统计,换热器进风表面风速分布如图5 所示,叶轮展向分布基本一致,论证了后续二维界面计算的可行性。
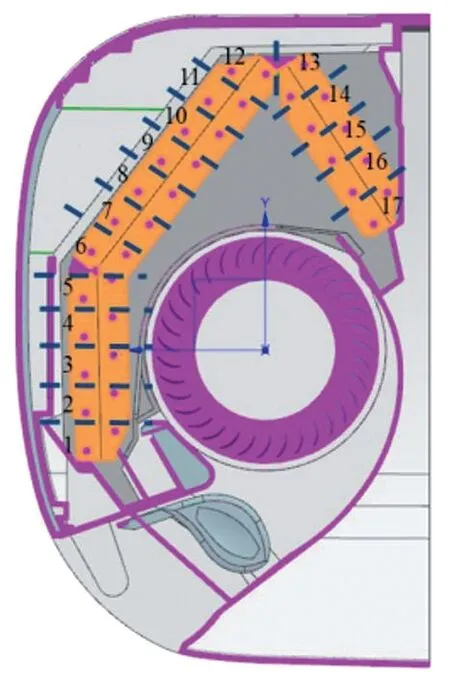
图4 风量分段统计示意图

图5 横向进风风速分布云图
统计不同转速下流经各段的风量占比,统计结果如图6 所示。计算结果表明,不同转速下分流分配基本一致,在做整机系统仿真时可以只做额定转速的风量分配,其他转速参照额定转速分配,进而提高仿真计算效率,统计还发现,挂机三段式蒸发器,前中后的总风量占比分别约为25%、45%、30%。
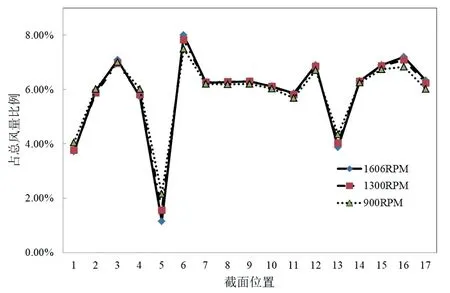
图6 不同转速下三维仿真计算风量分配分布图
2.2 二维替代三维可行性分析
在2.1 节的基础上,补充计算了二维仿真计算,并将结果分别与试验值、三维结果做对比,表3 为相关统计数据。

表3 不同转速二维与三维分析数据
结果表明二维仿真相较实测,不同转速下(900 rpm、1 300 rpm、1 606 rpm)总风量差异-7.58%、1.04%、4.53%;二维相较三维,不同转速下(900 rpm、1 300 rpm、1 606 rpm)风量差异0.37%、-1.74%、-2.23%,二维仿真模型计算结果与三维相比差异不大,可以很好地预测总风量。从速度场截面看(如图7 所示),风速分布位置、偏心涡位置也没有差异。

图7 不同仿真模式下的截面速度云图
图8 展示了不同转速下二维与三维关于17 段风量分配的仿真计算结果,相较三维,二维计算的各段风量占比偏差统计值在±0.7%以内,可用二维替代三维做风量分配计算。
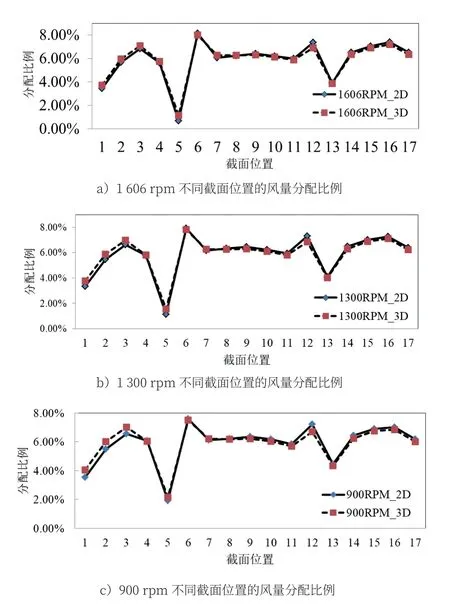
图8 不同转速二维与三维仿真计算的风量分配
综上所述,使用二维仿真替代三维进行总风量及风量分配计算具备可行性。
2.3 结果应用
本研究的初衷是为空调一维制冷系统仿真在挂机应用中提供一种简便可靠的风量及分布方法,关于制冷系统仿真模型搭建本文不做具体介绍,只将研究结果进行应用效果展示。
利用上述研究方法,在1.5 P φ7 蒸发器上进行分流设计,通过制冷剂环路的温度分布进行应用效果验证。换热器分流设计的理论设计图与管路焊接实物图如图9 所示,制冷剂上下两路从进口到出口各布置5 个温度点。判断分流设计优劣的一个重要指标是换热器不同流路出口温度分布的一致性,制冷剂环路不同位置的温度分布对比如表4 所示。仿真数据显示,在该工况下,只有蒸发器出口的每一路最后一只管出现过热,且上下两路出口的温度分别为14.00℃和14.20℃,处于较好的分流设计状态。将该分流设计制作样件测试,试验数据也是每一路最后一只管处于过热状态,出口温度高度一致,差值仅为0.15℃,很好地验证了应用二维仿真替代三维进行风量及分布计算的可行性。通过优化分流,实现了换热器换热量从3 450 W 提升到3 563 W,换热量提升3.3%。

图9 某型号换热器分流设计图

表4 制冷剂环路不同位置试验与仿真温度对比(单位:℃)
3 结束语
本文通过不同转速下的仿真与试验对比,从总风量、分布进行仿真试验对比,论证了二维替代三维计算风量及进风表面分布的可靠性,得出以下结论:
(1)调试的模型及网格策略在900 rpm、1 300 rpm、1 606 rpm 三种转速下的总风量及分配的仿真试验对比偏差在8%以内,仿真计算精度可靠。
(2)二维仿真模型计算结果与三维相比差异不大,偏差在3%以内,可以很好地预测总风量,17 段风量分配的仿真计算结果表明,相较三维,二维计算的各段风量占比偏差统计值在±0.7%以内,可用二维替代三维做风量分配计算。
应用二维仿真替代三维进行风量及分布计算的方法,通过制冷系统各路分流的表面温度分布情况验证了方法的可靠性。通过优化分流,实现了换热器换热量从3 450 W 提升到3 563 W,换热量提升3.3%。
本文仅对进风总风量进行了试验对比研究,且从实际产品应用的角度判定了二维CFD 计算风量分配在制冷系统仿真中的可靠性。受限于篇幅,出风口二维及三维的仿真对比分析未在本文展开讨论。后续可以通过PIV 等测试方法,完善进出风口仿真与试验的可靠性研究。

