基于信息理论和概率假设密度的自适应多站多目标无源定位与跟踪算法

上海航天电子通讯设备研究所 黄凯旋 周兴云 石磊 胡荣庆

本文针对密集杂波和冲击噪声条件下的多站多目标无源定位与跟踪问题，基于信息理论和随机有限集提出一种新的自适应高斯混合概率假设密度（PHD）滤波算法。该算法引入渐消因子，基于新息的方差动态修正滤波增益，并采用KL 度量对量测更新步骤中多目标密度近似前后的差异进行衡量，在最小信息增量意义下对高斯元进行合并，得到更准确的多目标状态后验分布，提高了多站多目标无源定位与跟踪精度，并降低了冲击噪声等对估计结果的影响。本文给出了基于信息理论的自适应多目标跟踪算法的高斯混合实现方式，所提出的方法继承了PHD 滤波器的优点，具有较好的实时性和多目标跟踪性能。最后，采用仿真实验对本文提出的算法进行验证，实验结果证明了本文所提出算法的有效性和优越性。

1 多目标无源定位跟踪研究背景

多站多目标无源定位与跟踪是电子战系统需要完成的主要任务之一，完成战场环境中多目标的监视、预警等任务，该任务的完成需要估计多个目标的位置及运动状态。多目标无源定位与跟踪主要面临的难点在于：缺少目标的距离信息，容易产生大量的虚假量测，目标数目不确定，航迹存在新生、消亡；量测受到漏检、杂波以及冲击噪声等影响；目标和量测的关联信息未知。

电子战设备可以获取目标的角度信息，对侦察范围内的各目标的定位结果可以根据多站获取的角度信息进行交叉而得出。但是当侦察区域内同时出现多个目标时，可能会出现模糊解问题，即产生大量的虚假点迹，严重影响了目标的定位与跟踪结果，并且目标的出现和消失还存在不确定性[1]。

近年来，基于有限集统计学（Finite Sets Statistics，FISST）的多目标跟踪算法可以避免大量的目标-量测数据关联，并对多目标状态进行估计。该方法基于多目标的概率假设密度（Probability Hypothesis Density，PHD）函数或强度函数，显示该函数的积分结果为多目标的数目。通过引入航迹标签[2]可以在多目标状态分布的基础上得到具体的航迹。PHD 滤波器具有良好的实时性和估计性能，并被用于机动目标跟踪、弱小目标检测前跟踪、扩展目标跟踪[3]及群目标跟踪等应用场景。基于粒子滤波的实现方法在理论上是最优的，但是所需要的计算量较大，而高斯混合PHD 算法在高斯元的合并步骤中，仅仅将均值和方差简单地进行加权组合，降低了跟踪精度。此外，量测还可能受到冲击噪声等非高斯噪声的干扰，影响了传统高斯混合PHD 方法的估计性能。

本文提出一种新的基于信息理论的自适应高斯混合概率假设密度滤波器。在矩匹配的条件下对高斯混合密度进行合并，采用KL 度量衡量高斯元合并前后多目标状态分布的差异，并建立相应的目标函数，在最小信息增量意义下得到最优的多目标状态后验分布，通过在贝叶斯框架下传递多目标状态分布，推导目标数目不确定、漏检和密集杂波条件下的多站多目标无源定位与跟踪方法。针对冲击噪声的影响，引入渐消因子，通过滤波信息的大小动态调整滤波增益，提高了算法的鲁棒性。本文给出了基于信息理论的自适应多目标跟踪算法的高斯混合实现方式，并通过仿真实验对本文提出的算法进行验证，实验结果证明了在密集杂波条件下所提出方法在多目标定位与跟踪性能上的提升。

2 基于信息理论的自适应高斯混合PHD 算法

电子战设备可以获取目标的角度信息，对于侦察范围内，各目标的位置可以用多个设备获取的角度信息进行交叉定位得出。但是当侦察区域内同时出现多个目标时，可能会出现模糊解问题，即产生大量的虚假点迹。

假设目标运动模型为线性高斯模型，如式（1）、式（2）所示：

其中， N(x;m,P)表示均值为m，方差为P的高斯密度函数，Fk-1是状态转移矩阵，Qk-1是过程噪声方差阵，Hk是量测矩阵，Rk是量测噪声方差阵。目标新生概率为pS,k(x)=pS,k，检测概率为pD,k(x)=pD,k，那么新生目标随机集的状态分布具有高斯混合的形式，如式（3）所示：

（1）多目标状态预测。k时刻预测PHD 具有如式（4）所示的高斯混合形式：

（2）基于信息理论的量测更新。假设k时刻预测PHD具有高斯混合形式，如式（8）所示：

则k时刻后验PHD 具有如式（9）所示的高斯混合形式：

公式（9）中，wk,n、mk,n和Pk,n是个高斯元聚类之后基于信息理论得到的均值和方差，如式（10）、式（11）、式（12）所示：

上述公式中，、、分别是高斯元基于量测更新得到的权重、均值和方差，计算过程如式（13）-式（18）所示：

其中pD,k是检测概率，是量测似然函数，是杂波密度函数，trace 表示矩阵的迹。从更新步骤可以看出，通过在贝叶斯框架下传递高斯混合形式的多目标状态分布，可以得到多目标的后验状态分布，在目标数目不确定、漏检、杂波以及冲击噪声条件下得到多目标的跟踪结果。

与传统的高斯混合PHD 相比，本文所提出的自适应高斯混合PHD 滤波器的计算量有所增加，主要在于高斯元的聚类以及渐消因子的计算。从更新公式中可以看出，这些计算量的增加是线性的，因此所提出的方法继承了PHD 滤波算法良好的实时性。

3 仿真实验

假设场景中目标新生概率为pb=0.02，传感器对目标的探测概率pd=0.95，目标幸存概率ps=0.98，由于多站定位的虚假点和量测虚警，在目标运动范围内平均每个时刻产生20 个杂波。目标的运动包含了匀速（CV），匀加速（CA）和协调转弯（CT）模型，量测获得目标的距离和角度，方差为其中并且量测以概率0.05 受到方差为100m2的冲击噪声的影响。

提出的I-GM-PHD 算法中高斯元裁剪门限为Ttr=10-5，每个时刻最多保留的高斯元个数为Jmax=200。当高斯元融合后权值大于等于0.5 时，该融合结果作为单个目标状态的估计结果。采用目标数目估计值和最优子模式匹配距离（OSPA）距离对结果进行评价。为x,之间距离，其中c为截断距离，即当x,之间距离大于c时取d(c)(x,)=c。记Πk为集合{1,2,...,k}上的所有排列，此处k为自然数集合N。另外记非负整数集合为取1≤p＜∞，c＞0，集合之间的距离定义如式（9）所示：

如果n≥m

将本文所提出的I-GM-PHD 方法与传统GM-PHD算法进行比较，并根据目标数目估计结果和OSPA 距离衡量多目标定位与跟踪性能。

如图1 所示给出了多目标数目估计结果和位置估计误差，可以看出，本文所提出的I-GM-CPHD 方法在估计精度上明显更好。原因在于，本文所提出的方法在高斯元的合并中基于信息理论在KL 度量条件下计算了目标状态的最优分布。目标的位置估计和方差均优于传统方法，并且通过渐消因子动态调整滤波增益，降低了冲击噪声对估计精度的影响。随着估计结果依据时间不断迭代，明显地提高了密集杂波和冲击噪声条件下的鲁棒性。

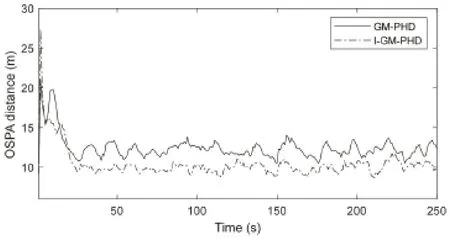
图1 每个时刻平均包含10 个杂波条件下的跟踪精度比较Fig.1 Comparison of tracking accuracy under the condition that each time contains 10 clutter on average

4 总结

本文针对密集杂波和冲击噪声条件下的多站多目标无源定位与跟踪问题，基于信息理论和随机有限集框架提出了一种新的自适应高斯混合概率假设密度滤波算法。所提出的方法采用KL 度量衡量量测更新步骤中多目标状态分布近似计算前后的差异，在最小信息增量意义下对高斯元进行合并，得到信息理论下更精确的多目标状态后验分布；此外，通过引入渐消因子，动态修正滤波增益，降低了冲击噪声对估计结果的影响，提高了算法的鲁棒性和雷达多目标的跟踪精度。仿真实验表明，本文提出的算法在目标跟踪精度上比传统方法有所提高，并且在密集杂波条件下的鲁棒性更强。

引用

[1] 何友,王国宏,陆大金,等.多传感器信息融合及应用[M].北京:电子工业出版社,2007.

[2] LIN X D,ZHU L H,WANG Y.Improved Probability Hypothesis Density(PHD)Filter for Multitarget Tracking[J].Control & Decision,2011,26(9):213-218.

[3] GRANSTROM K,NATALE A,BRACA P,et al.Gamma Gaussian Inverse Wishart Probability Hypothesis Density for Extended Target Tracking using X-band Marine Radar Data[J].IEEE Transactions on Geoscience and Remote Sensing,2015,53(12):6617-6631.