基于DRO的小行星往返飞越探测轨道设计优化方法*

董博文 于锡峥 李明涛 王楷铎 王有亮

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

0 引言

在地月系统内，远距离逆行轨道（Distant Retrograde Orbits, DRO）本身能级较高，接近地球影响球边界引力势。同时，这类轨道有较好的动力学稳定性，这使得其轨道维持和进出轨道的成本相对较低。由于DRO靠近月球，便于借用月球引力变轨，对地月空间范围内的其他轨道有较好的可达性[1]。有研究于2015年左右提出捕获近地小行星并将其安置在DRO的计划[2,3]。

近地小行星蕴藏着太阳系早期形成与演化的线索，对近地小行星探测具有重要科学意义。同时，近地小行星撞击也是面临的重大安全风险。无论是地球上的岫岩陨石坑、Barringer陨石坑等[4]，还是月球、水星、火星等太阳系其他天体上记录的撞击坑，都证明了天体间碰撞的数量之多。1976年的吉林陨石雨和2013年的车里雅宾斯克（Chelyabinsk）陨石等事件说明，小行星与地球的碰撞仍在持续发生且有可能造成严重破坏，不能无视这方面的威胁，因此需要对其进行探测。

文献[5]对DRO中转的深空探测飞行模式进行了论证分析，认为这是一种理想的探测方式。文献[6]对DRO前往火星与LEO前往火星的转移轨道进行了比较，以小行星采矿补给为背景，相较于从LEO出发，从DRO出发可以减少大约2.4 km·s-1的速度增量。现有DRO与地球间转移轨道，通常位于白道面内，而太阳系内的近地小行星大多相对白道面存在一定的倾角。在目前部署过的隼鸟（OSIRISREX）等近地小行星探测任务中，探测目标各不相同，但航天器均通过地球借力抬升倾角以飞抵小行星，飞抵小行星时航天器与地球距离远，且飞抵小行星所需时间长[7-9]。而在考虑飞越距离等约束条件后，小行星的最佳飞越点可能不在白道面内，使得飞越探测轨道相对白道面有较高的倾角，现有设计方法一般难以适用于有特定高倾角约束的轨道设计[10-18]。目前有少量关于如何在DRO与高倾角月球低轨道之间转移的研究[19]，但还缺少完整的地球与DRO间高倾角转移轨道的研究。

本文假设以DRO作为探测器的部署基地，研究从DRO中转，出发飞越探测小行星并返回至DRO的轨道设计方法。使用地月引力辅助对这类轨道的设计方法进行研究，降低了任务中的总速度增量，从而实现了高倾角地月转移轨道的设计。此外，引入了DRO调相机制，将DRO轨道站的相位同地球与DRO间转移轨道的设计解耦。

1 动力学模型

1.1 航天器动力学模型

研究场景航天器主要受到地球、月球与太阳的引力作用。为简化模型，忽略航天器对其他天体的引力作用，构建地球—月球—太阳—航天器四体模型（见图1）。三个天体的引力通过质点模型进行计算，保留地球和月球的尺寸，分别视作6378 km和1738 km半径的球体。以地球惯性系为基础构建力学模型，将月球和太阳引力作为第三体引力进行计算。探测器的加速度表示为

图1 地球—月球—太阳—航天器四体模型Fig.1 Earth-Moon-Sun-spacecraft four-body model

其中，µearth，µmoon，µsun分别为地球、月球和太阳的引力常数；R和r分别为探测器与地球相对位置及距离大小；Rmoon和rmoon分别为探测器与月球相对位置及距离大小；Rsun和rsun分别为探测器与太阳相对位置及距离大小。

1.2 DRO轨道计算

地月空间中的DRO是围绕月球运转的一类大尺度轨道，相对地球，在惯性空间中DRO是顺行轨道，而在地月会合坐标系（ROT，x方向从地心指向月心，z方向在月球相对地球的角动量方向，y方向遵照右手螺旋系确定）中，DRO绕月球逆行运转，如图2所示。在圆形限制性三体问题（CRTBP）中存在完全周期性的DRO轨道族，其具有相对其他三体轨道族更好的稳定性，能够承受更强的扰动而保持其准周期性[20]。

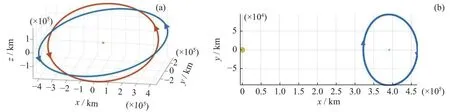
图2 远距离逆行轨道 （a）地球惯性系 （b） 地月旋转坐标系Fig.2 DRO track diagram.(a) Earth’s inertial system, (b) Earth-Moon rotating coordinate system

定义为DRO沿y轴正向穿过地月连线的状态，PDRO为DRO轨道周期，σ为相位因子，则DRO上任意一点的状态xDRO(σ) 表示为

其中，φ为以为初始状态，从t0到t积分CRTBP动力学方程所得到的解[21]。

在考虑轨道能量等方面后，DRO轨道站使用2∶1周期共振的平面DRO，以此为例研究DRO调相方法以及后续的DRO进出等其他方面。

2 问题分析与思路

2.1 探测轨道设计问题

轨道设计的目标是航天器在距离地球2×107km的范围内，在速度增量不超过2 km·s-1的条件下实现对近地小行星的往返飞越探测，期间相对地球高度不小于200 km，相对月球高度不小于50 km，即航天器地心距re≥6578km，月心距rm≥1788km。整体的轨道设计实现航天器从DRO轨道站出发，并在飞越小行星后返回轨道站。约束条件与参数使用整理列于表2。

进出轨道站时航天器状态设定为与轨道站相同，即出发、返回时航天器与轨道站位置速度相同。

以太阳中心二体模型的虚拟小行星作为探测目标，其轨道参数如表1所示。为减少轨道的速度增量，使用遗传算法对飞越点进行优化，得到的结果与黄道面有较大的距离，飞越时小行星与黄道面间的位置关系如图3所示。在考虑相关约束后，小行星飞越探测轨道需要被设计为高倾角。

表1 虚拟目标小行星轨道参数Table 1 Target asteroid orbit parameters

表2 常数取值与约束条件Table 2 Constant values and constraints

图3 飞越小行星时黄道面与各天体的关系Fig.3 Relationship between ecliptic plane and celestial bodies during asteroid flyby

2.2 轨道设计思路

如果要在约束下实现上述目标，有DRO直接转移和借力转移两种方式。DRO直接往返的小行星飞越探测轨道限制只在DRO出发、返回点以及小行星处进行机动，在DRO轨道站机动出发后直接逃逸离开地月空间，视目标小行星为质点，在飞越小行星时再进行一次机动，最后返回轨道站机动停泊。在设计时首先通过星历搜索小行星近地点时刻，之后在该时刻附近通过遗传算法在求解兰伯特问题的基础上对从DRO直接往返的小行星飞越探测轨道初值进行搜索，最后在四体模型下结合约束条件调整完成该情形下的轨道设计。轨道整体设计如图4所示。

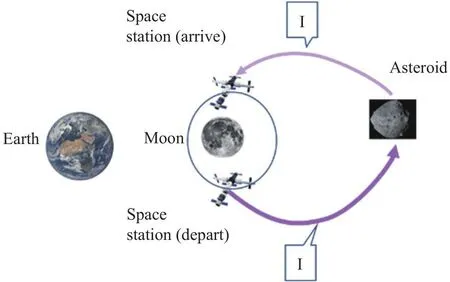
图4 DRO直接转移轨道整体设计（I表示DRO直接往返的小行星飞越探测轨道）Fig.4 DRO direct transfer orbit overall diagram(I expresses DRO direct return asteroid flyby orbit)

而在借力转移的DRO往返的小行星飞越探测轨道设计中，首先设计的部分是地球往返的小行星飞越探测轨道，之后再根据近地点参数设计地球往返DRO的轨道，最后对轨道两端在DRO的相位进行调整，与DRO轨道站相衔接。借力转移轨道整体设计如图5所示。

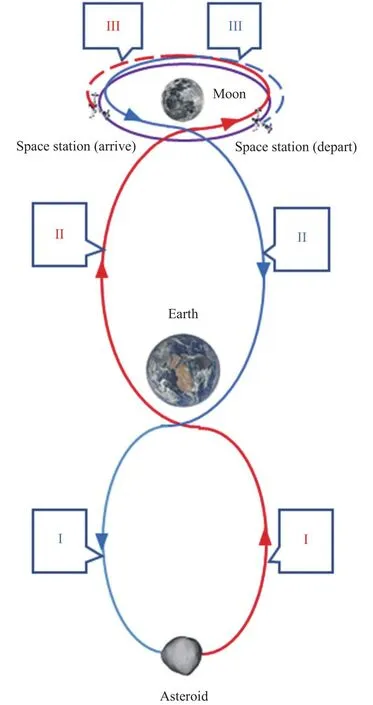
图5 借力转移轨道整体设计（I：地球往返的小行星飞越探测轨道。II：地球与DRO间转移轨道。III：DRO调相轨道）Fig.5 Overall schematic diagram of transfer orbit by force (I: asteroid flyby detection orbit of Earth round trip.II: Earth DRO transfer orbit.III: DRO phase orbit)

在地球往返小行星的飞越探测轨道设计过程中，航天器被设计为只在飞越小行星时进行一次机动返回地球，根据二体下的搜索结果，在四体模型中对轨道进行修正。在航天器小行星飞越点偏离黄道面时，探测轨道在近地点的速度方向与黄道面间存在较大倾角。由于白道面与黄道面接近，飞越探测轨道与白道面间存在相近大小的倾角。

在地球与DRO间转移轨道设计中，主要考虑地球、月球高度等约束条件，通过中途机动和月球借力实现对航天器位置和倾角等的调整。为降低优化设计的复杂度，参考文献[5]中DRO轨道的设计方法，将航天器轨道与Oxz平面的交点作为截止点和调相阶段起始点。

针对调相起始点存在偏差的情况，本文利用调相设计思想，实现了航天器与DRO轨道站的转移轨道设计。

以表1所示的虚拟小行星作为目标，优化得到的地球往返的小行星飞越轨道相对白道面有较大倾角，出发时为59.99°，返回时为59.88°，飞越小行星时的速度增量为0.085 km·s-1，轨道如图6所示。

图6 地球往返的小行星飞越探测轨道（ECI，左侧点为小行星位置，右侧点为地球位置）Fig.6 Earth round-trip asteroid flyby orbit（ECI.The left point is the location of the asteroid and the right point is the location of the Earth）

3 研究方法

3.1 基于月球借力的地球与DRO间转移轨道设计方法

3.1.1 设计方法

研究中地球与DRO间转移轨道起始于小行星飞越探测轨道的近地点，截止于月球借力后到达ROT坐标系的Oxz平面，包含近地点机动、中途机动和近月点机动三次机动。其中，近地点机动和近月点机动均在速度方向，中途机动方向在三维空间中不做约束，中途机动时间在另外两次机动之间且有至少一天的间隔。因此，该部分轨道优化包含近地点机动量dvep、中途机动dVm、近月点机动量dvmp和中途机动时间tm共4个变量，总体目标是使用尽可能小的速度增量在约束条件下使得调相起始点尽可能接近DRO远地点，即目标函数可视为调相起始点与DRO远地点之间的位置偏差drOxz、速度偏差dvOxz和3项机动的大小。问题可表示如下。

优化问题0

其中，t0为航天器到达近地点的时间，tmp为航天器到达近月点时间，Vs和Rs分别为航天器的速度和位置，tep，Vep0，Rep0分别为飞越探测轨道近地点的时间、速度和位置。总体流程如图7所示，其中优化问题1到5在后续进行介绍。

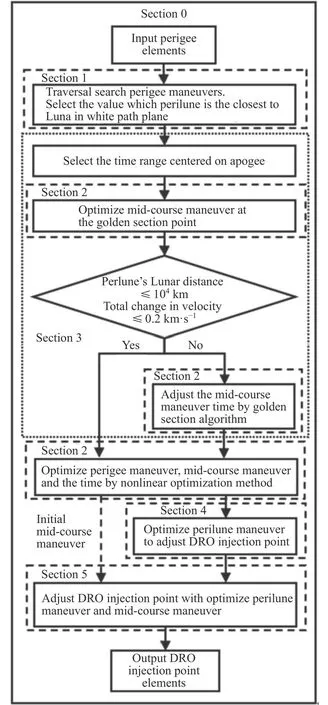
图7 遍历与黄金分割方法结合的轨道初值搜索方法DRO往返地球轨道设计流程Fig.7 Ergodic search method combined with the Golden section method schematic diagram of the DRO_Earth round trip orbit design flow

设计方法包括近地点机动量初值搜索、中途机动初值以及时间与近地点机动量搜索优化、近月点机动量与中途机动的优化确定三个部分，这三个部分依次完成。

轨道设计过程中结合使用遍历、非线性优化算法与黄金分割法，并根据约束确定目标近月点月心距rma。此外，从DRO前往目标近地点的轨道使用逆向积分经过相同流程进行设计。

3.1.2 近地点机动量初值搜索

使用遍历搜索近地点机动量dvep，保留使近月点白道面投影与月球距离rmw最小的数值作为初值dvep0，可概括如下。

优化问题 1

3.1.3 中途机动初值、时间与近地点机动量搜索优化

该部分由黄金分割法搜索嵌套非线性优化算法构成，对航天器在近地点与近月点之间的轨道进行设计。其中非线性优化算法对中途机动dvm初值与近地点机动量dvep共同进行优化，初值分别使用[0,0, 0]和dvep0，在得到中途机动初值dVm0的同时对dvep进行确定。该过程的中途机动时间tm视为常数。

非线性算法的目标函数由B平面参数Br和Bt近月点轨道参数近月点轨道倾角im、轨道月心距rmoon、近月点方位dθm和速度增量大小| dvep|，| dVm|等构成。其中前5项参数在优化时有目标Bra，Bta，ima，rma和dθma，直接作为优化目标的是5项参数与目标的差值大小dBr，dBt，dim，drmoon和Δdθma。

5项参数中B平面参数的目标值须经计算确定。在对地月转移轨道优化时，目标B平面参数的平方根，即入射双曲线轨道的b参数，可通过入射C3和目标近点中心距ra进行计算， 即

其中，µ为中心天体引力常数。当b参数符合式（3），轨道高度即可满足要求。

参考文献[22]中共面逃逸的目标参数计算，B平面参数可以通过b参数和角度θ表示，有

而θ可以由cosθ=确定，其中i和δ分别为入射方向渐近线与参考平面的夹角和双曲线轨道相对参考平面的倾角。由此可看出，双曲线轨道的最大倾角为i=π-|δ|，此时cosθ=-1，sinθ=0，又因DRO相对月球在白道面内逆向旋转，所以近月点处的B平面参数计算以白道面作为参考，取参数目标值为

关于后三项，由于轨道倾角的目标是与DRO相同的，ima=π；轨道高度目标是3.1.1中在约束条件下给定的rma；近月点方位目标是对借力方向进行调整，借力方向在从DRO出发时目标是从前方飞越抬升倾角，在返回DRO时是从后方飞越降低倾角，以月地连线方向为0°，以自北向南俯视时的逆时针方向为正，出发时dθma，返回时dθma。

在具体落实过程中，由于目标函数在落入极小值后不易向最小值继续搜索，优化问题以月球影响球范围的量级10000 km为界，当月心距在范围内外使用不同的目标函数。当月心距大于10000 km时，优化问题表示如下。

优化问题2

在月心距小于10000 km时，优化目标变换为

中途机动时间tm由黄金分割法单独进行调整。具体是在远地点时间附近以黄金分割法搜索中途机动时间，搜索范围取在远地点前后。使用1.3节中的方法，将所取黄金分割点的时间代入优化问题2中求解，使用所得结果对黄金分割法的目标函数值进行计算。问题可以表示如下。

优化问题3

3.1.4 近月点机动量与中途机动的优化确定

最后对近月点至调相起始点的轨道进行设计，该部分主要对近月点机动量dvmp进行优化，与中途机动dVm共同作为优化变量，目标函数包括调相起始点与DRO远地点之间在ROT坐标系中的位置速度差别 drOxz， dvOx与速度增量大小| dvmp|，dVm。

该部分首先在3.1.3节中所得近月点参数的基础上对dvmp进行初步优化，优化问题如下。

优化问题4

其中，t1为航天器到达近月点的时间，tmp，Vmp0和Rmp0分别为根据3.1.3节计算得到的近月点时间、速度及位置。

之后将优化问题4得到的近月点机动量以及优化问题2和优化问题3得到的中途机动作为初值，将优化问题2和优化问题3得到的中途机动时间tm位置Rm和初始速度Vm作为起始状态，优化截止于调相起始点的轨道，目标函数包括drOxz，dvOxz，| dvmp|，| dVm|，可以表示如下。

优化问题5

其中，tmid为航天器到达中途机动点的时间。

3.2 DRO调相轨道设计方法

航天器到达调相起始点时往往不能正好到达轨道站，存在相位偏差，需要进行调整以进行交会。DRO调相轨道以DRO轨道站为一端点，调相起始点为另一端点。

在轨道设计过程中先后使用遗传算法和非线性优化算法，优化变量包括调相轨道一端的速度增量dVp1和中间的滑行时间tp，优化目标包括总速度增量dvp和递推结果与轨道站目标的位置差别drp。该部分优化问题可以表示如下。

优化问题6

其中，tOxz为航天器到达调相起始点的时间，tOxz，VOxz，ROxz.分别为3.1节中得到的调相起始点时间、速度和位置。算法流程如图8所示。

通过这种方法可以对任意相位进行调整，速度增量成本在0.1 km·s-1左右，相位差别越大速度增量成本越高；在调相起始点与该相位上DRO存在偏差时，速度和位置的偏差对速度增量成本均有影响。其中，在DRO迹向的速度和法向速度以及位置偏差对于速度增量成本的增加效果更为显著。如图9所示，调相轨道起点的速度各方向偏差1.250 km·s-1，位置（径向和法向）偏差5000 km，相位差135.2°，共需约0.236 km·s-1的速度增量实现航天器与轨道站交会。同时，DRO轨道站的相位与DRO往返地球的轨道设计实现解耦，轨道的整体设计得到简化。

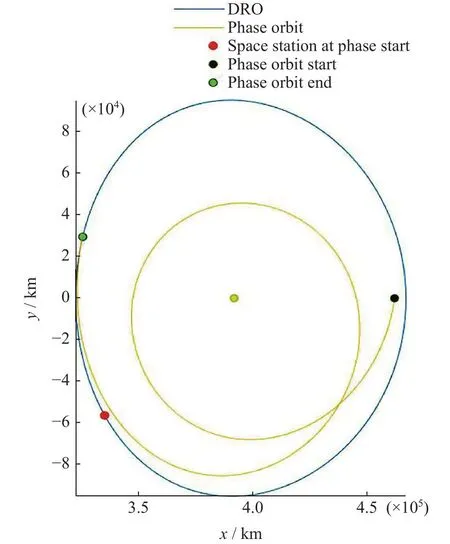
图9 调相轨道示例Fig.9 Sample phase modulation orbit diagram

4 设计仿真结果与分析

4.1 转移轨道设计仿真结果

以表1所示参数的虚拟小行星为探测目标，经过遗传算法和非线性优化方法的优化后，结果中从DRO直接往返的总速度增量为4.188 km·s-1。其中，出发1.924 km·s-1，返回1.825 km·s-1，深空速度增量为0.439 km·s-1，轨道如图10所示。

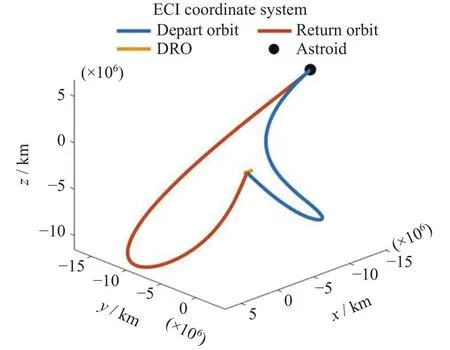
图10 DRO直接往返的小行星飞越探测轨道（ECI）Fig.10 DRO direct round trip asteroid flyby detection orbit（ECI）

因此，直接往返DRO不能满足关于速度增量的约束条件，需使用地月引力作为辅助来减少轨道的速度增量。

在借力转移的DRO往返的小行星飞越探测轨道设计当中，以如表3所示的地球飞越小行星的往返探测轨道的两个近地点作为后续地球往返DRO的轨道设计约束条件。在2×107km的约束下，尽管小行星相对黄道面的倾角不大，但飞越探测轨道的近地点存在较大的白道面倾角。

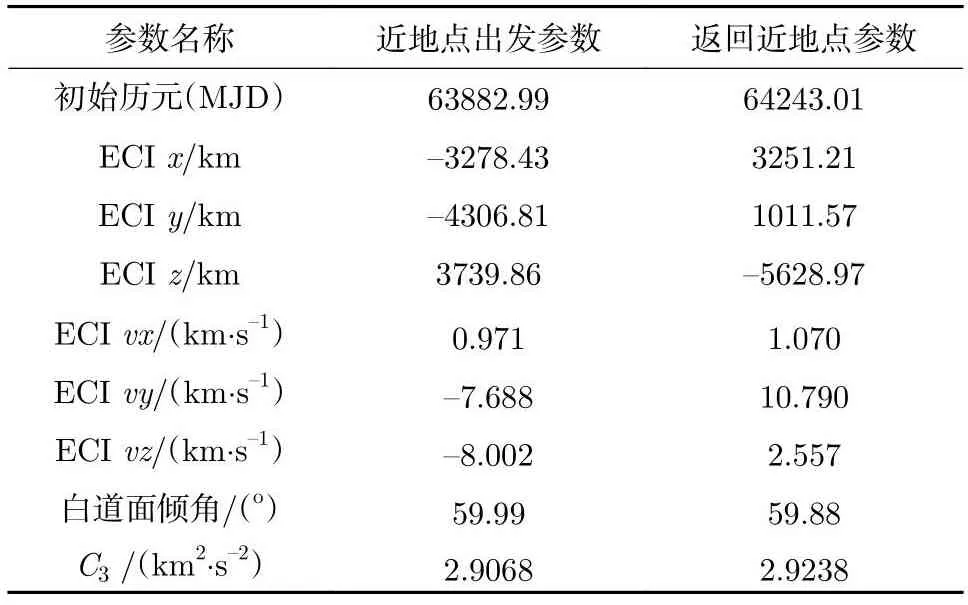
表3 飞越探测轨道近地点参数Table 3 Perigee parameters of flyby detection orbit

以上述近地点作为目标，使用前文3部分中方法对地球与DRO间转移轨道进行设计，转移轨道各项参数如表4所示，图像分别如图11和图12所示。

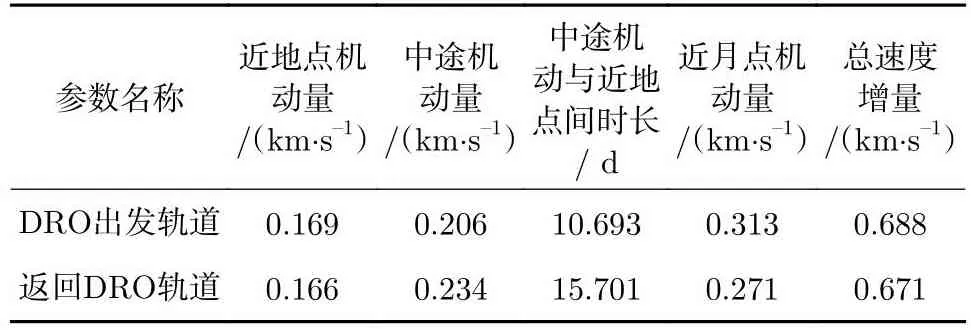
表4 地球与DRO间转移轨道各项参数Table 4 Perigee parameters of flyby detection orbit

图11 出发时地球与DRO间转移轨道Fig.11 Earth DRO transfer orbit at departure

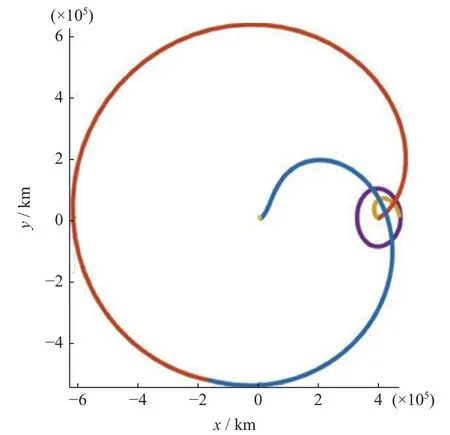
图12 返回时地球与DRO间转移轨道Fig.12 Earth DRO transfer orbit upon return

出发与返回时的调相轨道分别如图13和图14所示，各项参数如表5所示。在调相轨道设计结果中，单次机动的速度增量大约在100 m·s-1，其大小受调相起始点与DRO远地点间的位置和速度偏差影响显著。

表5 DRO调相轨道各项参数Table 5 Elements of DRO phasing orbit

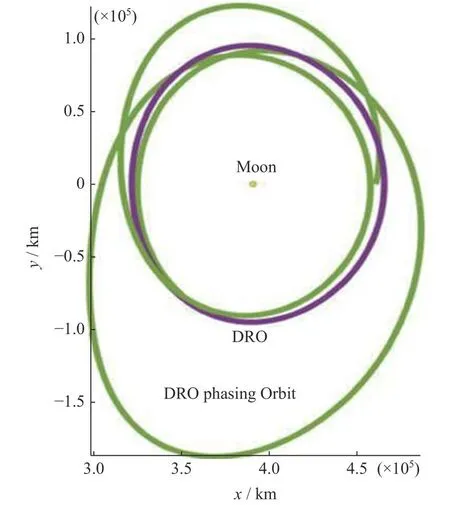
图13 出发时DRO调相轨道Fig.13 DRO phase orbit at departure

图14 返回时DRO调相轨道Fig.14 DRO phase orbit upon return

4.2 结果分析

从上述结果分析，地月引力辅助对航天器从DRO往返近地小行星有重要意义。在DRO直接出发前往小行星的情况下，表1中小行星的飞越探测轨道总速度增量为4.188 km·s-1，不能满足约束条件。而通过地月引力辅助，探测轨道总速度增量为1.973 km·s-1，包括DRO出发轨道总速度增量0.916 km·s-1、返回DRO轨道总速度增量0.972 km·s-1和飞越小行星时的速度增量为0.085 km·s-1，速度增量减少了50%以上。在直接往返DRO时，由于交会轨道站时速度小，且速度与机动方向之间存在较大夹角，速度增量对航天器动能的改变效率较低。

由此可见，使用DRO轨道站作为中转点时，通过地月引力辅助可有效减少航天器逃逸的速度增量。此外，在地球往返的小行星飞越探测轨道近地点白道面倾角较高的情况下，可通过月球借力与中途机动结合完成转移，有效减少了轨道改变倾角所需的速度增量。

5 结论

DRO可作为深空探测任务良好的中转轨道选择，有效减少任务中往返的速度增量成本，本文以近地小行星的飞越往返为例进行了说明，提出一种与常用方法不同的小行星飞越探测轨道流程。在高倾角转移轨道的情况下，通过月球借力可以有效减少改变倾角所需要的速度增量，出发和返回时航天器的速度增量均有明显减小，可在2 km·s-1的约束下实现更高倾角的飞越探测。例如所举算例，使用该方法可以减少50%以上的速度增量。

研究场景以DRO上某一确定的轨道站作为航天器的部署点以及返回后的回收点，航天器的起止轨道被固定在白道面附近靠近月球的位置。本文引入了DRO调相对此进行解决，通过在DRO处对相位进行进一步调整，DRO轨道站的相位与地球与DRO间转移轨道设计可以实现解耦。

参考二体情形下的情况，杠杆机动选择在远地点附近，能够以较小代价改变倾角、近地点等轨道参数。在使用的四体模型时这一点仍然近似成立，在仿真优化中发现在远地点附近能够找到更小的中途机动。这一点在较为复杂的模型中存在明显的偏差，如何进行证明还有待研究。