月球熔岩管探测中月表杂波识别方法仿真*

马士璇 董晓龙 朱 迪 马剑英 白东锦

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

0 引言

月球熔岩管是天然形成的地下管道，在火山活动中熔岩流的上部冷却结壳而下部继续流动时会形成一个洞穴，即熔岩管。一些光学测绘结果和基于重力测量的实验证据[1]均表明月球上极有可能存在大量比地球上尺寸大得多的熔岩管[2]。

月球的熔岩管可能提供躲避陨石撞击，抗辐射以及躲避月球表面极端温度变化的空间[3-6]。因此，月球熔岩管道的探测对于未来的空间探索，特别是月球的探测和利用具有重要的意义[7]。

2009年日本发射的探月卫星SELENE（月亮女神）号发现了三个直径和深度都为几十米的天窗。这些天窗被认为是熔岩管道局部塌陷后形成的[8]，对SELENE上搭载的测月雷达（LRS）的回波数据进行分析后指出天窗下方存在熔岩管。但也有研究认为，对SELENE号回波数据的分析存在问题，这些回波信号可能是月表杂波[9]。

在过去几十年的月球探测中，光学测绘和合成孔径雷达提供了大量的月球表面高分辨率的信息，包括地形地貌、物理性质和地质特征等，但是对月球的地下结构了解十分有限。光学测绘只能绘出月表的特征，合成孔径雷达追求高分辨率，因此大多采用较高的工作频率，而高频信号的穿透特性较差。因此，需要根据月球熔岩管探测的科学目标设计和研制月球熔岩管探测雷达，用以对月球表面以下熔岩管结构特征进行探测和科学研究[10]。

探地雷达用于星球地下结构探测也存在一定的限制。目前的探地雷达多是安装在地面可移动设备上，地面平台可以使探地雷达以较小的功率获得良好的分辨率，但设备的移动范围受到了很大的限制。

对于星载平台，为了获取较大的探测深度，所采用的探测频率通常较低，因此雷达探测波束较宽，进而导致来自月表的表面杂波与来自地下熔岩管的回波无法判别。随着探测深度的增加，熔岩管的回波功率呈指数衰减，更加难以从月表回波中分辨出来。因此，如何分辨地下回波和月表杂波，就成为对月球熔岩管探测的关键问题。

本文提出采用双频电磁波功率比的方法对熔岩管回波与月表杂波进行区分[11]。其主要原理是利用低频电磁波在月壤中路径衰减慢而高频电磁波在月壤中的路径衰减快这一特点。对于月表的杂波，由于未经过月壤，不存在月壤中的路径衰减，因此在高低频回波功率比上与熔岩管回波具有显著区别，据此判断回波的来源。

本文主要通过建立仿真系统，对不同频率，不同尺寸，不同埋藏深度的熔岩管可探测性进行分析，并对采用双频电磁波对熔岩管与地下目标进行分辨的理论进行验证，分析采用不同的频率对熔岩管进行分辨的能力。

1 熔岩管仿真结构

熔岩管的地下结构通常被假设为地下的空心半圆柱，如图1所示。图1中假设月球地层外为真空，熔岩管内部为真空，月球地层部分采用相对介电常数等电特性对其进行描述。

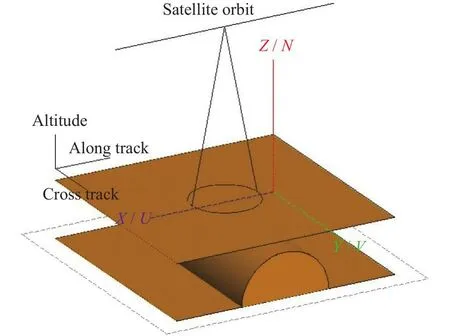
图1 三维熔岩管观测几何Fig.1 3D lava tube observation geometry

在已有的研究中，通过重力测量进行的结构稳定性分析给出了熔岩管的基本尺寸，即最大的熔岩管半径可达2.5 km[2]。而熔岩管的长度通常假设为几十公里[12]，因此本文研究针对长度为公里级的熔岩管。

月球表面的照片显示，一般情况下月海表面没有规则的几何特征。因此月球表面的地形可以用高斯随机粗糙面来模拟。

月球地层的相对介电常数所采用的模型是Bruggeman-Hanai-Sen混合模型[13,14]，模型公式为

式中，ε为相对介电常数，ρ为介质体密度（g·cm-3），(9.8+0.1i)是在假设零孔隙度的月球材料的介质体密度为3.5 g·cm-3的条件下的相对介电常数。在此基础上，Olhoeft等[15]通过对一百多个月球土壤和岩石样品的测量结果进行分析，利用最小二乘拟合，得到简化的介质体密度与相对介电常数的关系，即

式（2）描述了月球表面材料体密度与相对介电常数的关系，结合月球介质体密度与表面材料深度的关系，可以得到月球表面材料的深度与相对介电常数的关系的估计值。即深度与介电常数的关系可以写为

式中h为地下深度。

图2为月球地层介电常数。根据文献[15]，图2中的A线源于Frisillo等的研究，B线源于Carrier等的研究，A′(B′)和A′′(B′′)为与估计值相差正负一个标准差的曲线。本文选用B线作为仿真使用的介电常数。月球地层损耗正切δ如图3所示[16]。

2 双频熔岩管分辨原理

采用双频电磁波分辨熔岩管回波与月表杂波的理论推导如下。

月表的回波功率为

式中，Pt为发射功率，Ps,n(θ)为接收功率，G1(θ,fn)和G2(θ,fn)分别为天线在该方向上的双程方向图，σs0(θ,fn)为月表的后向散射截面，λ为波长，d为反射点与探测器的距离。

地下界面的回波功率为

式中，σss0(θ,fn)为熔岩管的后向散射截面，z为探测深度，R为菲涅尔反射系数，α为双程衰减系数，其计算公式为

设低频电磁波频率为f1，高频电磁波频率为f2，则可以给出双频电磁波回波功率，如图4所示。

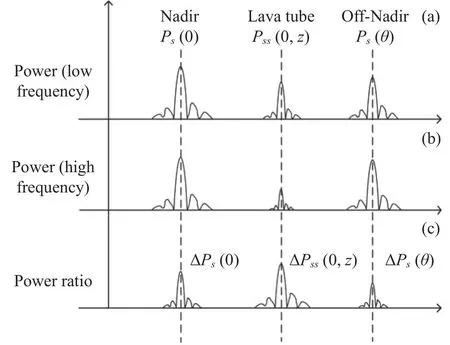
图4 双频回波功率及功率比Fig.4 Dual frequency echo power and power ratio diagram

由式（4）和（5），低频电磁波的月表回波功率与高频电磁波的月表回波功率之比ΔPs(θ)为

低频电磁波的地下界面回波功率与高频电磁波的地下界面回波功率之比ΔPss(θ)为

因此可给出低频回波功率和高频回波功率比的示意图，如图4所示。

由于f1＜f2，有

根据上述分析，采用双频电磁波，通过低频回波功率与高频回波的功率比，可有效区分月表目标与地下目标。

当回波来自于熔岩管目标时，低频回波功率与高频回波功率比会随熔岩管的埋藏深度而增加。当回波为月表杂波时，低频回波功率与高频回波功率比会随远离天底点而减小。

3 熔岩管探测雷达系统设计

月球熔岩管探测雷达系统设计，需要首先对熔岩管探测中的主要限制，即回波功率、分辨率、信杂比和信噪比等参数进行分析。基于上述参数对仿真系统参数进行设计，并对熔岩管的可探测性进行研究。

3.1 熔岩管回波功率

地下回波的衰减主要由两部分导致。一是在界面间的反射导致的功率损失，二是在介质中的衰减。

界面间的反射导致的损失可由菲涅尔反射定律计算，菲涅尔反射系数的计算公式如下：

式中，εi和εj分别为入射介质和折射介质的介电常数，θ为入射角度，s和p分别为入射波的两个分量。

在介质中的衰减则由电磁波衰减系数给出，其公式为

其中，f为电磁波频率，z为反射界面深度，α为双程衰减系数

由式（5）可推得地下界面的回波功率为

通过上式可以计算出熔岩管回波功率。

3.2 探测分辨率

3.2.1 垂直分辨率

高度向分辨率为

式中，c0为光速，B为信号带宽，ε为相对介电常数。由式(14)可知，垂直分辨率由带宽、相对介电常数决定。对于熔岩管目标，其高度向分辨率非常重要，而过小的熔岩管回波功率小，探测难度大，因此分辨率为5 m可满足大部分熔岩管探测需求。带宽为17.321 MHz即可满足分辨率需求，为方便计算，本文采用的带宽为20 MHz信号。

3.2.2 顺轨分辨率

顺轨方向采用合成孔径技术，其分辨率为

式中，λ为波长hi为飞行高度，Ls为合成孔径长度。由上式可知，合成孔径长度是影响顺轨分辨率的主要因素。合成孔径长度通常设定为天线的波束宽度，对于探月雷达通常使用的半波偶极子天线，其波束宽度为78°，因此同样在顺轨分辨率为5 m的条件下，电磁波频率只需高于15 MHz即可实现顺轨向高分辨。

3.2.3 交轨分辨率

交轨分辨率通常用脉冲限制直径描述，即

交轨分辨率是这一雷达设计中的主要限制，由于卫星的足印大且在交轨方向无法使用合成孔径等方式提高分辨率，导致交轨分辨率通常在1000 m以上，因此成为了对分辨率的主要限制。

3.2.4 分辨率分析

基于以上对分辨率的分析可知，单星探测熔岩管的交轨向分辨率通常在千米以上，顺轨分辨率由于可以采用合成孔径方法而更小，因此走向为交轨方向的熔岩管更容易实现有效探测，而对于走向为顺轨方向的熔岩管，受限于交轨分辨率，探测难度更大。所以以下分析皆基于熔岩管走向为交轨方向。

3.3 信杂比

研究月球的表面杂波，需要采用数值方法计算月表散射特征，因此必须对月球表面进行建模。二维粗糙面的计算量相比于一维粗糙面增大许多。当只在一个维度上粗糙，在另一个维度上几乎不变化的情况，可以用一维粗糙面代替二维粗糙面进行模拟。

但对于月表来说，粗糙面是二维的，是否能用一维粗糙面代替二维粗糙面以研究其反射特性，He[17]利用矩量法研究了一维粗糙面的散射特性，并与其他利用微扰法对二维粗糙面的散射特性研究进行对比，在0°～80°范围内，月表发射率仿真结果基本一致，证明了一维粗糙面可以描述二维月表散射特性。

月球表面的照片显示一般情况下月海表面没有规则的几何特征。因此月球表面的地形可以用高斯随机粗糙面来模拟。

粗糙面通常用其离开一个参考平面的偏差来描述其高度分布。在自然界的各种随机粗糙面中，应用最广的为高斯随机粗糙面。高斯粗糙面定义为表面高度分布的自相关函数为高斯分布的表面，有

其中，lx为相关长度，即相关函数的值变为1/e 时x的取值。

也可以采用功率谱密度描述随机粗糙面，一维高斯随机粗糙面的功率谱密度为

其中，hδ为均方根高度，k为波数。

描述粗糙面的特性常用均方根高度hδ和相关长度l两个参数，也可以采用均方根斜率tanθ对粗糙面进行描述。

探月中用到的月表粗糙度测量方法主要包括光学立体相机[18]和激光高度计[19]，通过上述两种载荷首先得到月球表面高程数据，然后计算粗糙度参数[17]，即

对于月球表面，已有粗糙度参数的研究为均方根高度0.4±0.1m，相关长度2.8±0.7m[20]。

利用功率谱密度，粗糙面可以用蒙特卡罗方法来模拟生成。通过蒙特卡罗方法可以由下列函数生成长度为L的一维粗糙表面样本[21]，即

式中，xn=nΔx，n=-N/2+1, ···,N/2。xn表示粗糙面上第n个采样点，F(kj)与f(xn)称为傅里叶变换对。F(kj)的定义如下：

式中，kj为离散波数，定义为kj=2πj/L，N(0,1)为符合标准正态分布的随机数。

完成随机粗糙表面建模后，即依据粗糙面样本计算后向散射系数。

微扰法（SPM）适用于高度起伏较小的粗糙表面，即粗糙面的均方根高度和相关长度都小于入射波长。微扰法的适用条件需要粗糙面的均方根高度小于入射电磁波波长的5%左右[22]。同时，表面均方根斜率必须和波数与均方根高度的乘积在一个数量级上，这两个条件的数学表达式为

月表粗糙面参数可以满足上述条件，根据微扰法，计算得到后向散射系数，即

式中，k为波数，hδ为均方根高度，θi为入射角，l为相关长度；αpq为极化系数，有

极化系数中，εr为相对介电常数，θi为入射角度。

根据后向散射系数式（23）与式（5）可以计算出月表杂波功率。结合式（12）熔岩管回波功率，即可获得所需的信杂比。

3.4 信噪比

对于探测采用的甚高频频段，银河系宇宙噪声对探测的影响相当大。噪声

式中，k0=1.380649×10-23J·K-1为玻尔兹曼常数；B为带宽；T(f)为噪声温度，该噪声温度和频率有关[23]。

信噪比即为

其中Pr为熔岩管回波功率。

3.5 熔岩管仿真参数

基于上述分析可以得出结论，影响熔岩管检测能力的主要因素是雷达信号穿过地层导致的衰减。对于月球表层这一有稳定相对介电常数和损耗正切的介质，地层的衰减主要取决于熔岩管的埋藏深度和中心频率。

对检测能力进行分析采用的发射功率综合考虑月球轨道探测器的体积、重量等因素，并参考现有的月球轨道探测任务。基于前述对功率、分辨率、信噪比和信杂比的分析，设峰值功率为800 W，天线增益设为半波偶极子的增益为1.64 dB，探测器飞行高度为100 km，探测频率分别为30 MHz，60 MHz和90 MHz进行计算，探测参数列于表1。

表1 雷达仿真参数Table 1 Lidar simulation parameters

4 仿真结果与分析

4.1 熔岩管可探测性分析

基于上述仿真参数，对熔岩管的回波信杂比与信噪比结果进行仿真，结果如图5～7所示。

图5 30 MHz回波信杂比与信噪比Fig.5 Echo signal SCR and SNR at 30 MHz

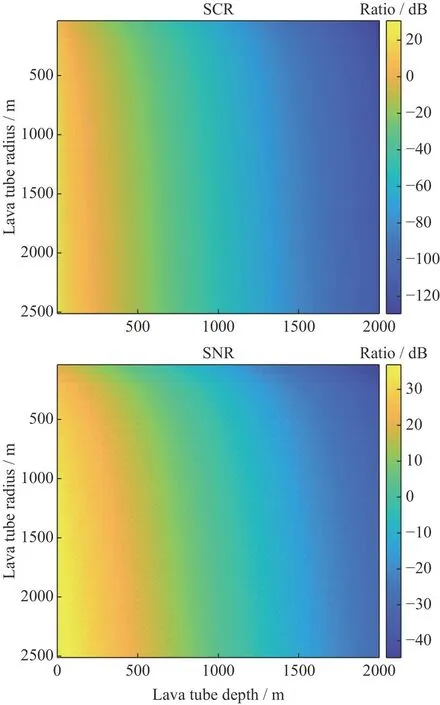
图6 60 MHz回波信杂比与信噪比Fig.6 Echo signal SCR and SNR at 60 MHz

图7 90 MHz回波信杂比与信噪比Fig.7 Echo signal SCR and SNR at 90 MHz

在熔岩管探测中，将满足SCR＞ 0 dB，SNR ＞10 dB并且顺轨向和交轨向均大于对应分辨率条件的熔岩管认定为可检测[24]。因此对于使用不同频率对不同尺寸和不同深度的熔岩管进行探测的可检测区域结果如图8所示。由图8可知，对不同尺寸和不同深度的熔岩管采用多频率探测的仿真结果表明，低频电磁波可以探测到更深的熔岩管，但对直径小的熔岩管没有探测能力。高频电磁波探测深度较小，但对直径小的熔岩管具备探测能力。

图8 不同频率下的熔岩管可探测性Fig.8 Detectability of lava tubes at different frequencies

4.2 仿真场景

为了研究交轨走向熔岩管探测场景，采用表1给出的雷达参数进行仿真。依据所采取的中心频率及对熔岩管可探测性的分析，本文对半径为150 m，走向为交轨方向的熔岩管进行研究，如图9所示。

图9 交轨走向熔岩管Fig.9 Orbit crossing towards lava tube

对图9所示的熔岩管采用PSTD解算器进行电磁仿真[25]，采用中心频率30 MHz的Chirp信号，熔岩管埋藏深度100 m，半径150 m。并利用脉冲探地雷达的后向投影算法对回波结果进行处理，所得结果如图10所示。其中深度100 m处明显界限为月表，可以看出，在深度200～350 m处有明显回波响应，并且其水平宽度约为300 m，可以有效的鉴别出图9中所示的熔岩管。

图10 熔岩管回波仿真结果Fig.10 Lava tube echo simulation results

4.3 双频区分熔岩管与月表杂波的仿真

通过使用多频率电磁波对熔岩管进行探测，可以有效地区分熔岩管回波和非天底点地形起伏导致的月表杂波。基于PSTD解算器生成回波，可对这一方法进行仿真验证。

4.3.1 回波功率比仿真

为验证使用双频电磁波对月表杂波与熔岩管回波进行区分的方法，首先构建熔岩管与月表仿真模型，如图11所示。对上述仿真建模采用30 MHz与60 MHz两个频率进行仿真，其归一化回波功率如图12所示。

图11 熔岩管仿真建模Fig.11 Lava tube simulation model

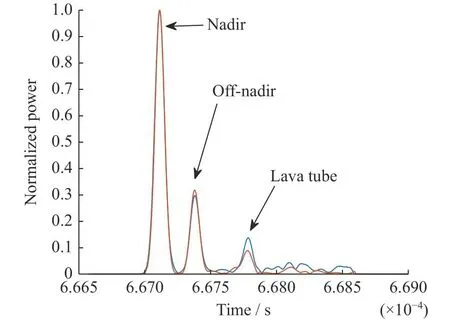
图12 双频回波归一化功率Fig.12 Dual frequency echo normalized power

图12的仿真结果表明，对于非天底点月表杂波，双频电磁波的回波功率相近，高频略高于低频。而对于熔岩管的回波，低频回波功率显著大于高频回波功率，因此采用高低频回波功率比区分月表杂波与熔岩管回波的方法是有效的。

4.3.2 多频熔岩管回波功率比

基于4.2节中应用PSTD方法进行的仿真验证，采用15 MHz，30 MHz，60 MHz，90 MHz四个频率对熔岩管探测进行仿真。回波功率比仿真结果如图13所示。图13中蓝线为低频频率15 MHz，高频频率30 MHz的回波功率比；橙线为低频频率30 MHz，高频频率60 MHz的回波功率比；黄线为低频频率60 MHz，高频频率90 MHz的回波功率比。其中，黄线仅在深度90 m以下存在功率比，是由于在深度90 m以下，90 MHz的频率已无法进行有效的探测，导致黄线的回波功率比仿真仅至90 m。

图13 多频熔岩管回波功率比Fig.13 Multi-frequency lava tube echo power ratio

4.3.3 回波功率比分析

图12所示的非天底点月表杂波归一化回波功率结果显示，非天底点的低频回波与高频回波功率比低于双频回波功率比。同时，熔岩管的低频回波与高频回波功率比高于天底点的低频回波与高频回波功率比。图13的多频回波功率比仿真结果表明，当所采用的频率比相同时，频率差越大，则通过回波功率比进行熔岩管回波和月表杂波区分的效果越好。当所采用的频率差相同时，频率比越大，则通过回波功率比进行熔岩管回波和月表杂波区分的效果越好。

4.3.4 基于DEM真实地形的回波功率比分析

基于上述功率比分析，采用双频电磁波对真实月球地形进行分析。所采用的月球区域为（77°N，113°W）附近的一段起伏地形，数据来源为嫦娥二号分辨率为20 m的数字高程模型。

根据图14的地形，假设其地下存在熔岩管，熔岩管模型构建如图15所示，仿真参数同表1，电磁波频率为30 MHz与60 MHz。

图14 （77° N，113°W）地形Fig.14 Topography of （77° N，113°W）

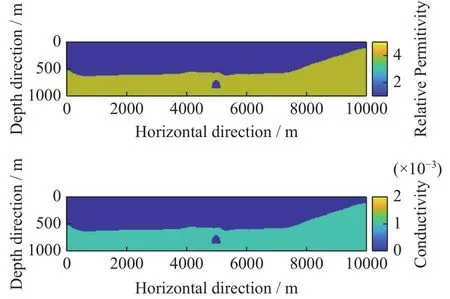
图15 DEM地形仿真建模Fig.15 DEM terrain simulation model

对上述地形进行仿真，归一化回波功率及平均功率如图16所示。从图16可以看出，在非天底点地形起伏区域，低频电磁波的回波功率小于高频电磁波。而在熔岩管的回波区域，低频电磁波的回波功率大于高频电磁波。因此，通过对双频电磁波功率比的分析，确实能够有效分辨出熔岩管回波与月表杂波。

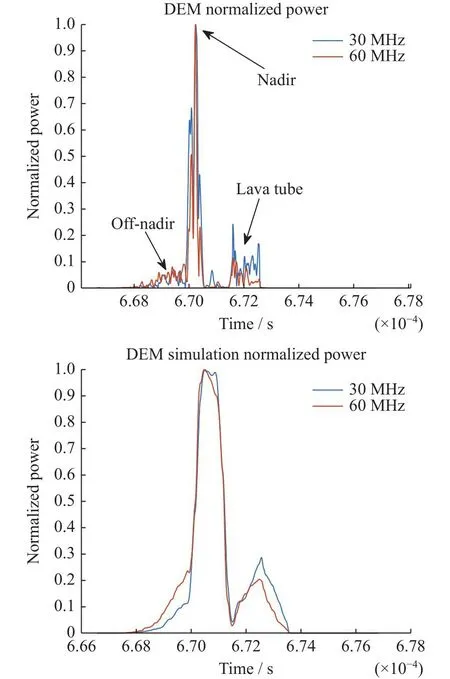
图16 真实地形双频回波功率Fig.16 Real terrain dual-frequency echo power

5 结论

光学测绘与基于重力测量的实验证据表明，月球下有可能隐藏着可利用的熔岩管。本文主要对各种尺寸，埋藏深度的熔岩管，通过理论分析与仿真，对采用不同频率电磁波进行探测的可行性进行了分析。研究了使用双频电磁波功率比对地形起伏导致的月表杂波与熔岩管回波的分辨的方法进行了理论分析，并通过电磁模拟，研究了不同频率的电磁波组合的分辨性能。

对于不同尺寸及埋藏深度的熔岩管可探测性研究的结果表明，在基于现有月球表面，月球地层的理论和研究，对月球表面及月球熔岩管进行建模仿真的条件下，90 MHz及以下的频率均可实现对不同尺寸熔岩管的有效检测，这些尺寸是基于月球熔岩管结构稳定性研究提出的。所使用的探测频率越高，可检测的埋藏深度越低。

对于采用双频率电磁波对月表杂波与熔岩管回波进行分辨的方法，在进行了理论分析的基础上，利用电磁仿真方法对多频回波进行了功率分析。结果表明，通过双频电磁波探测方法可以有效的分辨月表杂波与熔岩管的回波，并且熔岩管的埋藏深度越深，这一方法的分辨性能越好。

同时，采用多个频率组合对同一熔岩管进行研究，以分析频率对探测性能的影响。结果表明，所采用的频率比相同时，频率差越大，则通过回波功率比进行熔岩管回波和月表杂波区分的效果越好。当所采用的频率差相同时，频率比越大，则通过回波功率比进行熔岩管回波和月表杂波区分的效果越好。

通过理论分析与仿真研究了熔岩管的探测的回波功率、信噪比和信杂比等参数，对探测系统进行参数设计，给出了不同尺寸熔岩管的可探测性。提出并仿真验证了根据高低频回波的功率比分辨月表杂波与熔岩管回波的方法，研究了不同频率组合下该方法的分辨性能。并基于月球实际地形，对这一理论进行了仿真验证，为后续的熔岩管探测雷达系统设计与研制提供了参考。