页岩油储层径向井立体压裂产能预测模型研究

戴佳成，王天宇，田康健，李敬彬，田守嶒，李根生

中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

0 引言

我国油气资源消耗量与日俱增。2020 年我国油气表观消费量分别为6.69 亿t和3259.1 亿m3，油气对外依存度分别为73%和43%。加大对非常规油气资源的开发力度，对缓解油气消费快速增长与供应的矛盾，保障国家能源安全具有重大意义。页岩油是我国常规油气的重要接替资源，技术可采资源量达43.93 亿t，排名全球第三[1]。大庆油田预测地质储量12.68 亿t页岩油，更是标志着我国陆相页岩油勘探开发取得重大突破[2]。

我国陆相页岩油藏多属低渗或特低渗储层，地层能量低，储层的非均质性强，需大型水力压裂改造地层[3-5]。“水平井+多段水力压裂”是国内外开发页岩油的常用方法[6-7]。水平井压裂后形成的复杂裂缝可提高页岩油产能[8-10]，但目前仍面临单井压裂效果不明显，尤其是缝高受限制的问题。以古龙页岩油为例，受层理发育等因素影响，一般压裂裂缝高度仅10 m左右[11]，同时页岩油藏垂向渗透率极低，使得水平井压裂裂缝在垂向利用程度低。多数学者深入研究了如何提升水平井压裂水平开发程度[12-14]，但对垂向利用考虑仍较少。据统计，我国页岩油水平井压裂单井钻井和完井成本介于4000～6000 万元人民币之间[15-16]。虽然水平井压裂是目前开发页岩油的主要手段，但其不能适应所有的页岩油开发环境[17]，存在垂向利用需求时水平井压裂适应性较低的问题，故我国仍需探索一种能够有效增大缝控储量、降低施工成本和增加经济效益的页岩油藏改造新方法[18]。

2014 年，李根生等[19]针对煤层首次提出了径向井立体压裂技术。如图1 所示，其通过在主井的不同层位钻出多个径向微小井眼的前提下再实施压裂，可诱导裂缝起裂与扩展，形成三维复杂裂缝网络。径向井立体压裂可通过“多口直井，多个径向井，多层压裂”的方式经济地解决页岩油藏单个裂缝垂向井控范围弱的问题，较水平井压裂技术有明显优势。针对该技术，学者主要通过数值模拟和室内实验展开了径向井立体压裂时井周边应力场分布，裂缝起裂压力和裂缝形态研究。研究发现，径向井可改变地应力，对水力裂缝起到诱导效果，且可显著降低裂缝起裂压力[20]，增加缝网复杂程度，提高储层改造效果。卢玉义等人[21]使用水泥岩样预制径向井最高降低了69%裂缝起裂压力。付宣[22]发现径向井可在煤岩层理面水平起裂形成“一平多纵”的缝网形态。刘庆岭[23]建立了单层径向井裂缝起裂和拓展模型，得出分支数目大于4 时不利于形成多条垂直主裂缝的结论。郭肇权等[24]通过多层径向井立体压裂实验探究了裂缝形态受径向井方位角，水平应力差和径向井长度等因素的影响。

图1 径向井立体压裂示意图Fig.1 Demonstration of radial-borehole fracturing

径向井立体压裂技术已在中美俄[25-28]等国成功应用，有望成为高效经济地开发页岩油的革命性技术。目前径向井立体压裂产能模型较少，曲占庆等[29]假设裂缝垂直于径向井建立了单个径向井远端压裂段产能解析解。刘庆岭[30]采用离散裂缝法处理径向井立体压裂裂缝，提出了径向井压裂缝内流体半解析流动模型，模拟了单层多分支径向井压裂产能。水力裂缝的处理和耦合是压后产能模拟的关键，借鉴页岩油水平井压裂产能模型：在解析模型上中一般将水力裂缝中流动视为符合线性流动[31-32]。数值模型可以模拟更复杂的裂缝形态，除双孔双渗模型[33-37]外，使用嵌入式离散裂缝法可以考虑裂缝的具体形态，将裂缝流动降低一个维度后形成独立的裂缝流动体系[38-39]。

为探索径向井立体压裂开发页岩油藏的可行性，本文以大庆古龙页岩油参数为基础，描述了径向井立体压裂的缝网形态，建立了页岩油三维基质—裂缝—井筒跨尺度流动模型，进行了三维压后页岩油藏产能模型，分析和对比了水平井压裂和径向井立体压裂2种开发模式下的页岩油产能，并分析了径向井分支数，径向井层数和主井数目对产能的影响规律。研究结果有望为径向井立体压裂高效开发页岩油提供理论基础。

1 径向井立体压裂缝网形态

图2 展示了一种径向井立体压裂模式的缝网形态，即在等水平间距的3 口主井，等垂直间距的3 个层位分别喷射钻出4 个彼此垂直径向井分支孔眼后压裂。径向井井筒压力改变了井周应力场，每口径向井分别诱导一条裂缝，形成多条在近井处沿径向井方向扩展，随后裂缝方向逐渐朝向最大水平主应力方向的水力裂缝[30]。本文中主井间距相同，设为ΔL，单位m；同层径向井高度一致，层间距设为ΔH，单位m；同主井所有径向井和裂缝在水平投影上重合，即无相位差。

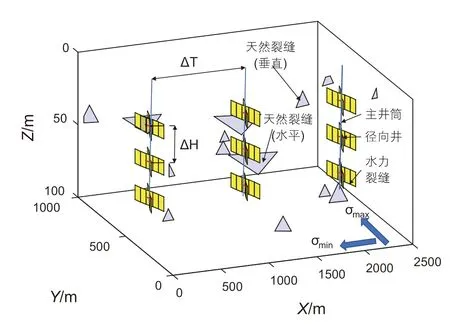
图2 径向井立体压裂裂缝形态示意图Fig.2 Schematic diagram of fractures system in radialborehole fracturing

径向井对水力裂缝有一定的引导作用，一般文献中使用引导因子这一概念量化该引导效果[40]。但引导因子不足以描述裂缝的具体路径。本文由参考文献[30]中对径向井立体压裂的裂缝形态研究成果，将裂缝简化为若干以节点相连的长方体流动单元，如图3 中黄色矩形所示。裂缝节点以主井筒为起点，沿径向井方向重合一段距离(诱导长度)后，裂缝节点逐渐偏向最大水平主应力方向，其在水平方向坐标可表示为：

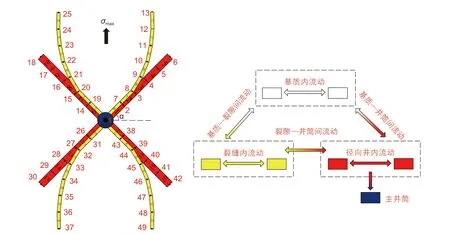
图3 径向井立体压裂网格划分与流动模型示意图Fig.3 Schematic diagram of radial well three-dimensional fracturing mesh and flow model

式中，li代表线段i的长度，m；βi代表线段i的相对最小水平主应力方向的角度，°，βi表示为：

式中，α代表径向井相对最小水平主应力方向的角度，°；dβ代表单位长度内角度变化，°/m。

页岩储层中的天然层理缝，页理缝和剪切缝发育[41]，本文采用开源软件Alghalandis Discrete Fracture Network Engineering(ADFNE)[42]分别生成了一组倾向水平和一组倾向垂直的随机分布的天然裂缝近似代替。如图2 中淡蓝色三角所示的部分裂缝，裂缝形态以三角形近似表示，且天然裂缝的边长，角度，倾角在指定范围内按指数随机分布。本文中天然裂缝生成后，在任何算例中其分布位置、几何参数和物性都不发生变化。

2 数值模型与求解

页岩油径向井立体压裂需要考虑基质，裂缝和径向井内部和之间的流体流动关系，目前径向井立体压裂三维产能预测模型较少。本文参考了页岩油水平井压裂模型，结合径向井立体压裂模式创新建立了三维基质—裂缝—井筒跨尺度流动模型，并考虑了水力主裂缝和人工裂缝的影响，进而计算页岩油径向井立体压裂的产能。模型假设如下：

1) 考虑油藏的垂向和水平渗透率差异，单一孔隙度。

2) 由于不存在注入井，假设边水能量充足，即边界设为恒压条件，且边界流入流体油饱和度和油藏内部一致；

3) 忽略页岩油在油藏内部流动时的析气，凝析和结蜡现象，忽略岩石和流体物性随压力的变化；

4) 忽略天然裂缝分布，忽略主水力裂缝伴生的微裂缝以及可能带来的井周基质渗透率提升。

本文按节点分析法将复杂的裂缝—井体系划分为以节点连接的流动单元[43]。以图3 为例，在一个四分支径向井中，裂缝、径向井和主井被分为由33 个流动单元和49 个节点组成的离散体系(省略了天然裂缝)。在此基础可以赋予各节点几何和物理属性，并可灵活地调整径向井立体压裂布井模式。径向井立体压裂流动体系包括基质、裂缝和井筒内部及相互间的流动。本文在以下对各流动规律进行简要介绍：

1) 基质内流动

页岩储层孔隙致密，一般认为流体在基质内流动呈现非达西特征，本文采用了文献中[44]的指数式非达西流动方程，结合质量守恒方程得：

式中，α代表油水两相中的一者；λα为相流度，D/(Pa·s)；Pα为相压力，Pa；ρα为相地层密度，kg/m3；g为重力加速度，取9.8 N/kg；Z为深度，m；Sα为相饱和度，无因次；φ为孔隙度，无因次；t为时间，s；qαnnc和qαw分别代表了基质和裂缝，井筒间耦合的质量源项，kg/(m3·s)；非达西项中的无因次非达西系数a和b可表示为相流度λα的函数：

2) 裂缝—基质间，裂缝内和裂缝间流动

压裂后页岩储层裂缝发育，本文采用嵌入式离散裂缝法(EDFM)将水力裂缝进行降维处理，三维裂缝在基质网格中被划分为若干平面，裂缝内流体满足N-S方程的流动等效为服从达西渗流规律[45-47]，并使用两点通量近似格式(TPFA)进行离散。在嵌入式离散裂缝法中，裂缝—基质间(即式(4)中耦合源项qαNNC），裂缝内部和裂缝间的流体流动规律可以统一表示为：

式中TNNC为非相邻连接单元(NNC)间传输系数，D·m。非相邻连接单元是在物理上相互连接但在计算网格间不相邻的单元，TNNC可表示为：

式中，kNNC，ANNC和dNNC分别表示非相邻连接单元间的渗透率、接触面积和距离，单位分别为D、m2和m。kNNC，ANNC和dNNC的表征方式随非相邻连接单元类型不同而变化，对应公式在文献[48]中有详细表述。

3) 径向井内，径向井—基质间和径向井—裂缝流动

将径向井内流动视为一维流动，则径向井内流动的质量守恒方程为：

式中，xα表示相体积分数，无因次。

径向井内能量守恒方程在忽略摩擦阻力后简化为伯努利方程[49]：

式中，相流速uα，m/s，可表示为：

式中，D为径向井直径，m。

径向井和基质及裂缝间流体流动耦合关系可表示为：

式中，Pbh为径向井压力，Pa；J为井指数，m3/(s·Pa)。在直角坐标系内，对于井筒—基质井指数可表示为[50]：

式中，kh为有效渗透率与净厚度的乘积，D·m；rw为井筒半径，m；re为等效半径，m；S为表皮系数，无因次；无因次参数θ随井筒—基质间耦合关系变化而变化。对于井筒—裂缝井指数可表示为[51]：

式中kf，裂缝渗透率，单位D；wf，裂缝宽度，单位m。

对基质，井筒和裂缝中控制方程进行离散，并以Newton-Raphson迭代法表示为：

式中，等号左项为雅可比矩阵，X为初始变量；k为当前时间步。

本文基于MATLAB Reservoir Simulation Toolkit(MRST)平台[52-53]对式(15)进行求解，其为一款基于MATLAB的用于油藏建模和模拟的免费开源油藏模拟软件，提供了全面的黑油和组分油藏模拟器，能够模拟行业标准模型，并包含图形用户界面，用于后期处理模拟结果。

3 模拟结果

3.1 参数设置和模型验证

本文以松辽盆地古龙页岩油藏青一段和青二段参数[54]为基础建立页岩油产能数值模拟模型，如表1 所示。由于页岩是页理和层理的广泛发育，垂向渗透率极低，故参数中垂向渗透率远低于水平渗透率，而孔隙度为单一值。为验证模型准确性，本文以文献中[55]A-1 水平井为例建立了页岩油水平井压裂产能模型，水平井位于油藏中心，采用定产液量90～160 m3/d方式生产，参数如表2 所示，网格划分如图5 所示。如图4 所示，实测井底压力和模型计算井底压力吻合，最大误差为3%，该误差是由于验证算例产液量有波动导致的。该验证证实了模型的准确性。

表1 页岩油藏参数Table 1 Shale reservoir parameters

表2 水平井压裂参数Table 2 Horizontal well fracturing parameters

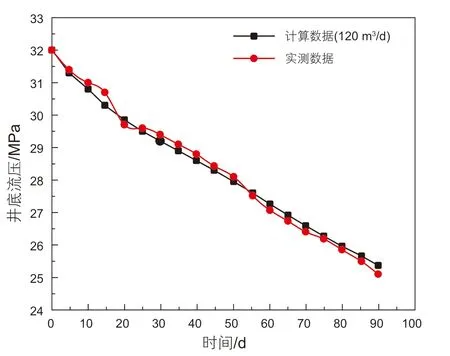
图4 A-1 井实测和计算井底压力Fig.4 Measured and calculated bottom hole pressure in well A-1

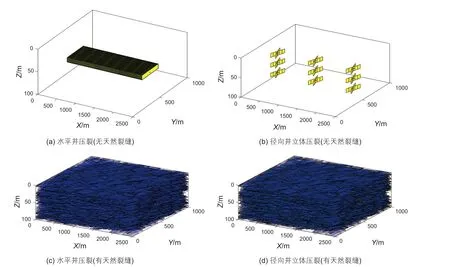
图5 算例网格划分Fig.5 Meshing of cases

为有效对比水平井压裂和径向井立体压裂，本文进一步建立了页岩油径向井立体压裂产能模型。径向井主井水平投影连线和水平井保持一致，且二者水力裂缝参数一致。径向井的分支数，长度，方向，裂缝的轨迹和参数参考了文献[30]，如表3 所示。为防止原油在地层内脱气，水平井和径向井的井底压力均设置为20 MPa。天然裂缝参数如表4 所示。

表3 径向井立体压裂参数Table 3 Radial-borehole fracturing parameters

表4 天然裂缝参数Table 4 Natural fracture parameters

本文将网格设为长25 m，宽25 m，高1 m的立方体，总网格数为4×106。模拟时长为3 y，步长30 d。

3.2 产能分析

本文通过页岩油压后产能模型预测了水平井压裂和径向井立体压裂(3 主井，3 层径向井，4 分支径向井)在无天然裂缝和有天然裂缝下生产的4 个算例，其网格划分如图5 所示，同一压裂模式的水力裂缝在无天然裂缝和有天然裂缝时完全一致。模拟时间为3 y，得到了储层压力沿过井筒的水平和垂直剖面分布随时间变化规律和产能时间关系。

3.2.1 无天然裂缝算例

在无天然裂缝条件下，径向井立体压裂可以获得更大的泄流区，径向井立体压裂第三年产油速率和油总产量是水平井压裂的2.25 倍，分别为56.3 t/d和6.3万t。计算结果证明了径向井立体压裂通过在直井和径向井的基础上获得了比水平井压裂更好的页岩油开发效果。

3.2.2 水平井压裂(有天然裂缝)

在存在天然裂缝的条件下，水平井，水力裂缝和天然裂缝共同构成了低压泄流区，使得泄流区边界不规则，如图6 所示。大量天然裂缝的存在显著改善了页岩油藏孔—缝—井间的流体沟通能力，尤其增大了垂向控制体积，使得水平井压裂产能较无裂缝条件取得了极大提升。其中，与水平井水力裂缝直接相交的天然裂缝数目为264 个。有天然裂缝下水平井压裂第三年产油速率和总产油量均为无天然裂缝时的7 倍，分别为174.5 t/d和19.7 万t。

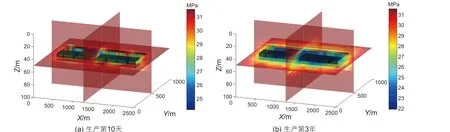
图6 水平井压裂(有天然裂缝)剖面压力分布Fig.6 Pressure distribution profile of horizontal well fracturing (with natural fractures)

3.2.3 径向井立体压裂( 有天然裂缝)

径向井和压裂裂缝网络可以沟通更多天然裂缝，形成多处不规则边界的泄流区，实现对页岩油藏的立体开发，如图7 所示。其中，与径向井立体压裂水力裂缝直接相交的天然裂缝数目为水平井压裂的1.35 倍，为356 个。计算结果证明了径向井立体压裂在有天然裂缝的条件下亦能取得比水平井压裂更好的页岩油开发效果，产油速率和第三年总产油量均为水平井压裂的2.3倍，分别为390.7 t/d和43.6 万t，如图8 所示。

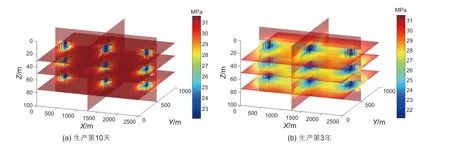
图7 径向井压裂(有天然裂缝)剖面压力分布Fig.7 Pressure distribution profile of radial-borehole fracturing (with natural fractures)

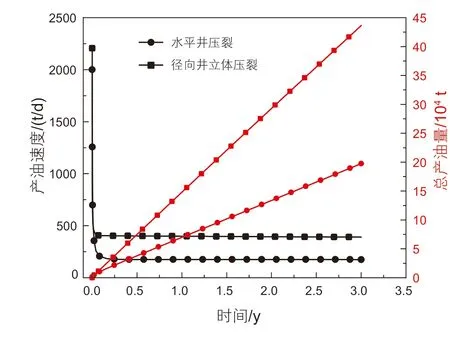
图8 径向井压裂(有天然裂缝)产能—时间关系Fig.8 Production-time relationship of radial wells fracturing(with natural fractures)

3.3 参数分析

为进一步验证径向井立体压裂的主要径向井钻井参数对产能的影响，本文在含有天然裂缝的页岩储层为基础，探究了径向井立体压裂径向井数，径向井层数和主井数目对产能的影响。选取第三年时产油速率和第三年总产油作为评价标准。

如图9 所示的是主井数目为1，径向井层数为1时产能随径向井数目增加的关系。各径向井间角度相等。当径向井从1 增加至4，第三年产油速率和总产油量均增加了1.8 倍。这是因为水力裂缝数量随径向井数目的增多而增多，同一个起裂点形成的泄流区面积增大。但随径向井数目进一步增大，多分支径向井诱导形成单条水平裂缝，不利于形成多条垂直主裂缝[30]。

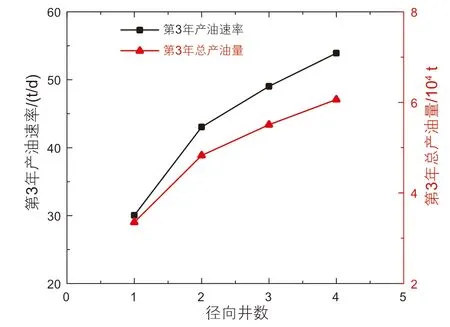
图9 径向井数与产能关系Fig.9 Relationship between number of branch and productivity

如图10 所示的是主井数为1，径向井井数为4 时径向井立体压裂产能随径向井层数的变化关系。径向井层间距离相等。当径向井层数从1 到4，第三年产油速率和总产油量分别增加了3.6 倍和3.8 倍，增产效果显著。径向井层数的增加可加强对页岩油藏的垂向开发，对开发垂向渗透率低的页岩油藏尤其具有指导意义。但受层高限制，当径向井层数大于3 时，增产效果逐渐减弱。

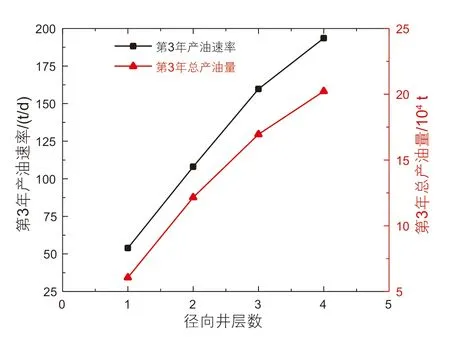
图10 径向层数与产能关系Fig.10 Relationship between number of layer and productivity

如图11 所示的是主井数为1，径向井分支数为4时径向井立体压裂产能随主井数的变化关系。当主井数从1 增加至4，第三年产油速率和总产油量均增加了1.8 倍。主井数的增加可加强对页岩油藏的水平开发，但是由于页岩油藏水平方向渗透率较高，裂缝发育较多，增加主井数带来的产能提升效果较弱。

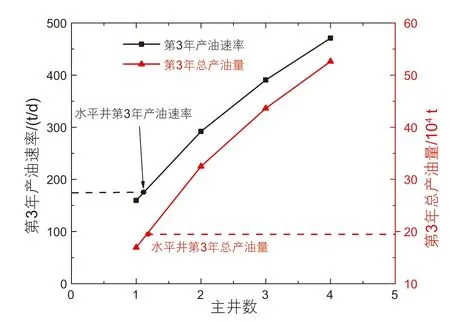
图11 主井数与产能关系Fig.11 Relationship between number of main well and productivity

综上，当径向井分支数为4，层数为3 时，主井数超过1，即可获得优于水平井压裂的产能。进一步地，径向井立体压裂不仅可以实现比水平井压裂更高的产能，还更具有经济性。考虑一口2000 m直井钻完井成本200 万元[56]，钻径向井眼成本为20 万/眼，压裂成本为100 万/层和地面建设成本200 万，3 井3 层4 分支径向井立体压裂成本共计2880 万元，远低于水平井压裂约4000 万的成本。

4 结论

本文针对水平井开发页岩油垂向利用程度不足的问题，创新提出“多井，多孔，多层”的径向井立体压裂开发设计理念，建立了页岩油三维基质—裂缝—井筒跨尺度流动模型，预测了不同参数下产能。本文的主要结论如下：

(1) 径向井立体压裂方法均比水平井压裂更有利于打破层间流动限制，可获得更大的垂直泄流区域，提高油藏控制体积和产能；

(2) 径向井立体压裂产能随径向井分支数，径向井层数和主井数的增加而增加，其中增加层数带来的产能提升最高；

(3) 3 层3 径向井立体压裂在有天然裂缝和无天然裂缝条件下的产油速率和总产油量均超水平井压裂的2 倍，充分证明了径向井立体压裂的可行性。