溯本追“圆”见真章 拨云见日得正解
谢洁红

俗话说:吃一堑,长一智。学习的过程也是一个修炼的过程,与难题过招,见招拆招;溯本追源,定能拨云见日。现对同学们在本章学习过程中常出现的几种典型错误进行分析,希望大家引以为戒。
一、忽视圆的相关概念
例1 下列结论:(1)过圆心的线段是直径;(2)弦是直径;(3)弧是半圆;(4)长度相等的两条弧是等弧。其中正确的有()。
A.0个B.1个
C.2个D.3个
【错解】B。
【错因分析】没有准确理解“直径”“半圆”“等弧”等相关概念。
【正解】弦与直径的联系和区别:弦和直径都是端点在圆上的线段,但直径一定经过圆心,故(1)(2)错误。弧可分为半圆、优弧和劣弧,故(3)错误。等弧是指能够完全重合的两条弧,故(4)错误。故选A。
【点评】本题考查了圆的相关概念,要注意“直径是圆中最长的弦,但弦不都是直径”“半圆是一条特殊的弧”。等弧的长度是相等的,但长度相等的弧不一定是等弧,还要看能否重合,所以在等圆或同圆中才有等弧。
例2 在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心、R为半径所作的⊙C与斜边只有一个公共点,则R的取值范围是()。
A.R=2.4
B.3<R<4
C.R=2.4或3<R≤4
D.R=2.4或3<R<4
【错解】A。
【错因分析】没有审清题意,从“只有一个公共点”仅得出直线与圆相切。
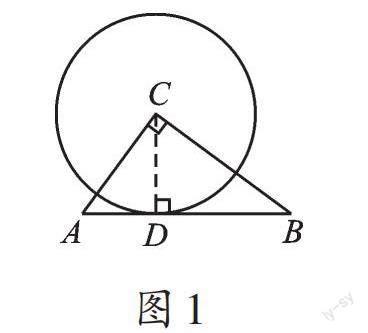
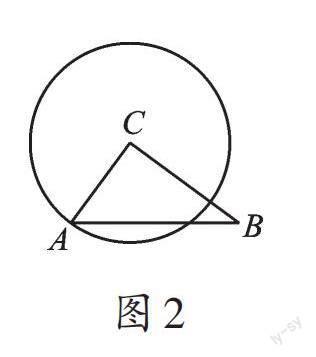
【正解】当⊙C与斜边AB相切时,如图1,此时,⊙C与斜边AB只有一个公共点。设⊙C与斜边AB相切于点D,则CD⊥AB。根据勾股定理和三角形的面积公式,可求出CD=[AC×BC/AB]=[3×4/5]=2.4,即R=2.4。当R=AC时,如图2,⊙C与斜边AB恰有两个公共点;当AC<R≤BC时,如图3,⊙C与斜边AB只有一个公共点;当R>BC时,如图4,⊙C与斜边AB无公共点。综上所述,R的取值范围是R=2.4或3<R≤4。另外,当R<2.4时,⊙C与斜边AB无公共点;当2.4<R≤AC时,⊙C与斜边AB有两个公共点。故应选C。
【点评】本题不能把“只有一个公共点”等同于“相切”。同时,我们还要注意条件给的是线段、射线还是直线。
二、忘记分类讨论,导致漏解
例3 已知△ABC内接于⊙O,∠OCB=33°,则∠A的度数为________。
【错解】57°。
【错因分析】只考虑点A和圆心O在BC的同侧,漏了在异侧的情况。
【正解】∵∠OCB=33°,OB=OC,
∴∠COB=114°。
(1)当点A1和圆心O在BC同侧时,如图5。
∴∠A1=[1/2]∠COB=57°。
(2)当点A2和圆心O在BC异侧时,如图5。
∴∠A2=180°-∠A1=123°。
所以∠A的度數是57°或123°。
【点评】一弦所对的圆周角有两个,且它们有互补关系。
(作者单位:江苏省无锡市硕放中学)

