土石坝渗流性态分析的IAO-XGBoost集成学习模型与预测结果解释

余红玲，王晓玲，任炳昱，郑鸣蔚，吴国华，朱开渲

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

1 研究背景

渗流数值模拟是分析土石坝渗流性态的一种有效手段，目前有许多不同的数值模拟方法应用于大坝渗流性态分析研究中[1-3]。虽然各种渗流数值模拟方法在大坝渗流场计算分析中发挥了重要作用，然而，复杂地质条件下的大坝渗流数值模型对计算资源的要求较高，求解时间较长，存在计算效率较低、难以实时分析大坝渗流性态的问题。基于机器学习方法的代理模型通过寻求输入变量与输出变量间的复杂响应关系，实现对复杂物理过程的近似描述，可代替真实系统快速给出所求解[4]。常用的代理模型包括径向基函数(Radial Basis Function，RBF)、Kriging模型、支持向量回归(Support Vector Regression，SVR)、多元自适应回归样条(Multivariate Adaptive Regression Splines，MARS)等单一代理模型以及由多种机器学习算法构成的组合代理模型[5]。基于机器学习算法建立大坝渗流数值模拟模型的代理模型，能够减少计算量、有效提高大坝渗流性态分析的效率。然而，现有机器学习算法大多将复杂的渗流数理机制作为“黑箱”处理，难以理解模型决策过程，导致模型可信度较低。因此，构建一种高效且具有可解释性的渗流性态分析模型具有重要的意义。

极限梯度提升(eXtreme Gradient Boosting，XGBoost)[6]是一种基于梯度提升的集成学习算法，其不仅具有较快的运算速度和较强的泛化能力，还能够对输入特征的重要度进行排序，具有一定的可解释性[7]。目前，XGBoost算法在国内外各领域应用较为广泛。在国内，张福浩等[8]基于XGBoost算法构建了滑坡隐患点识别模型，并通过特征重要性分析获得了影响滑坡发生的重要因子；张钧博等[9]将XGBoost算法应用于岩爆烈度分级预测研究中，并对岩石单轴抗压强度、单轴抗拉强度、洞室围岩最大切应力、岩石弹性变形指数和岩体完整性系数等指标进行了重要性分析；徐韧等[10]采用基于贝叶斯优化算法的XGBoost算法对大坝变形数据进行了预测，并通过特征重要性分析得出温度分量对大坝变形的贡献较大，而水压和时效分量的贡献较小；张书颖等[11]建立了基于XGBoost算法的纤维增强复合材料加固钢筋混凝土梁抗弯承载力预测模型，并对模型进行了特征重要性分析，确定了影响加固梁承载力的关键因素；丁阳阳等[12]将XGBoost算法引入煤体结构识别中，并结合特征重要性分析方法输出了模型构建中的敏感参数。在国外，Li等[13]采用XGBoost算法预测了企业研发投资的创新绩效，并通过特征重要性排序发现了影响企业创新绩效的关键因素；Su等[14]利用XGBoost算法建立了地表沉降的非线性智能预测模型，并通过XGBoost算法的特征重要性评估发现了决定地表沉降的最主要因素；Liu等[15]建立了基于XGBoost算法的纤维增强复合材料残余抗拉强度和模量预测模型，并通过特征重要性分析定量评价了各属性参数对预测结果的影响；Yan等[16]提出了基于XGBoost算法的装配式混凝土建筑投资估算模型，并通过特征指标重要性排序得出了影响投资估算结果的重要指标。

尽管传统的XGBoost算法可以通过特征重要性分析，挖掘影响预测结果的关键特征，但是这只能得出特征的重要程度，难以解释各特征对预测结果的影响[17]，模型可解释性有待增强。Shapley加性解释(SHapley Additive exPlanation，SHAP)是由Lundberg等[18]提出的一种用于增强机器学习模型可解释性的统一框架，可以对每一个样本的每一个特征变量计算出线性可加的贡献值，从而达到解释的效果[19]。与XGBoost算法的特征重要性分析相比，SHAP可以综合全局和局部两方面进行模型可解释性分析。首先，从全局出发，SHAP不仅可以对样本特征的重要性进行排序，挖掘影响预测结果的关键特征，还可以定性分析样本特征与预测结果的正负相关性；其次，从局部上看，SHAP可以显示出单个样本中各个特征对此样本的预测结果是如何起作用的，显著提高预测结果的可信度[20]。因此，本研究将XGBoost算法与可解释机器学习框架SHAP相结合，以建立具有较强可解释性的大坝渗流性态分析模型。

此外，XGBoost集成学习算法的模型超参数较多，超参数的设置对模型预测性能具有较大影响。现有研究大多根据人工经验或网格搜索方法搜寻XGBoost算法的最佳参数，难以获得最优参数组合。采用智能优化算法对超参数进行调整不仅能够获得最优参数组合，还可以减少时间，提升效率[21]。天鹰优化器(Aquila Optimizer，AO)是Abualigah等[22]于2021年提出的一种新型智能优化算法，具有较强的全局搜索能力和较快的收敛速度。然而，AO算法采用简单的随机方式对种群初始化，难以保证初始化种群分布的均匀性和多样性，并且在开发阶段容易陷入局部最优。通过混沌映射产生的混沌序列具备规律性、遍历性、随机性等特点，可以增加初始种群整体的均匀性和多样性[23]；天鹰飞行速率是AO算法开发阶段的重要参数，对其非线性化对于增强算法的局部搜索能力具有重要作用。因此，本研究提出基于混沌理论和非线性飞行速率更新策略改进的天鹰优化(Improved Aquila Optimization，IAO)算法，对XGBoost集成学习算法的超参数进行自适应调优，以提高XGBoost算法的预测精度。

综上所述，本研究在可解释机器学习框架SHAP下，提出一种基于IAO-XGBoost集成学习模型的土石坝渗流性态分析方法，有效解决现有大坝渗流数值模拟方法计算效率较低、难以实时分析大坝渗流性态，而基于机器学习方法的代理模型可解释性较差等不足，从而为大坝运行管理人员提供准确和可靠的大坝渗流性态分析结果。

2 研究框架

所提模型的研究框架如图1所示，主要包括数据集生成、基于IAO-XGBoost集成学习的预测模型建立、基于SHAP理论的预测结果解释和案例研究四部分。

(1)数据集生成。针对现有复杂坝基地质条件下的土石坝建模方法通常采用先建模后裁剪修型的方式，导致建模过程中涉及大量主观经验判断，容易影响建模准确性和建模效率的问题，采用基于有向地层分界面布尔逻辑序列(Boolean Logic Sequence of Oriented Geological Interfaces，BLSOGI)的多地质体自动建模方法[24]，自动建立复杂坝基地质条件下的大坝模型；然后，采用拉丁超立方抽样(Latin Hypercube Sampling，LHS)方法从上下游水位和各地层渗透系数的取值范围中抽取若干样本点，并将这些样本点输入基于CFD技术的土石坝渗流数值模型中，通过模拟计算获得渗流效应量的响应值，输入的样本点与输出的渗流效应量响应值则构成大坝渗流性态指标预测模型的数据集；将数据集划分为训练集和测试集，其中的训练集用于训练预测模型，而测试集用于检测预测模型的预测性能。

(2)基于IAO-XGBoost集成学习的预测模型建立。针对大坝渗流数值模拟方法存在计算效率较低、难以实时分析大坝渗流性态的问题，利用XGBoost算法预测精度高、运算速度快和泛化能力强的优势，建立大坝渗流性态指标的预测模型；进一步地，针对XGBoost算法超参数的取值问题，在传统天鹰优化算法的基础上，引入混沌初始化种群和非线性飞行速率更新策略进行改进，建立改进的天鹰优化(IAO)算法，并将IAO算法用于自适应优化XGBoost算法的超参数n_estimators、learning_rate和max_depth，从而建立基于IAO-XGBoost的大坝渗流性态指标预测模型，进一步提高大坝渗流性态指标预测的精度。

(3)基于SHAP理论的预测结果解释。针对基于IAO-XGBoost的大坝渗流性态指标预测模型仅能得出预测结果和输入特征的重要性排序，而难以深入分析各样本的特征如何影响预测结果的问题，将可解释机器学习框架SHAP理论与IAO-XGBoost算法相结合，在对特征进行全局重要性分析，挖掘关键特征的同时，分析输入特征对预测结果的正负相关性影响，并解释特征间交互作用以及单个样本的特征对大坝渗流性态预测结果的影响，从而提高预测模型的可信度。

(4)案例研究。将所提模型应用于中国西南某土石坝工程，通过对比分析验证所提方法的有效性和优越性。

3 土石坝渗流性态分析的IAO-XGBoost集成学习模型

3.1 XGBoost集成学习模型XGBoost是由Chen和Guestrin提出的一种基于梯度提升决策树(Gradient Boosting Decision Tree，GBDT)模型优化的集成学习方法[6]。XGBoost的基本思想是通过加入新的弱学习器拟合前一次训练的残差，并在训练结束时得到每个样本的预测分数，最后将所有弱学习器中的预测分数相加而获得样本的预测值[25]。目前，XGBoost已经成功应用于众多领域，且在训练样本有限、训练时间较短等场景下具有独特优势[25]。这些特性正好适合于根据渗流数值模拟数据建立大坝渗流性态指标预测模型。基于XGBoost建立大坝渗流性态指标预测模型的主要原理如下。

(1)

式中：fk为一棵回归决策树；F为所有可能的回归决策树的集合；K为回归决策树的总数；fk(xi)为第k棵回归决策树对第i个渗流性态指标样本xi的计算分数。

渗流性态指标预测模型训练过程中的目标函数是算法的核心，如下式所示：

(2)

(3)

式中ft(xi)为第t轮迭代时新加入的回归决策树。

对上式进行二阶泰勒展开并去掉常数项constant后，则目标函数表达为：

(4)

式中gi和hi分别为损失函数l的一阶和二阶导数。

进一步地，将目标函数转换为一个关于wj的一元二次方程求最小值的问题，即

(5)

(6)

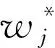
(7)

(8)

(9)

3.2 基于IAO算法改进的XGBoost集成学习模型XGBoost超参数较多，超参数设置不准确将导致大坝渗流性态指标预测效率低下、精度降低。然而，超参数优化过程实质上是一个黑盒函数优化问题，若优化参数过多，则容易使模型冗余，导致计算复杂性增加，并影响系统整体性能[21]。因此，本文仅选取对XGBoost算法预测性能影响较大的关键参数，如n_estimators、max_depth和learning_rate等超参数进行优化。其中，n_estimators 为集成算法中弱评估器的数量，此参数值越大，模型的学习能力越强，但模型也越容易过拟合；max_depth控制模型中树的最大深度，其值越大模型越复杂，且模型容易过拟合；learning_rate参数控制迭代速率，可以防止模型过拟合[26]。

现有研究大多根据人工经验或网格搜索方法搜寻XGBoost的最佳超参数。然而，依靠人工经验寻找超参数需要丰富的专业背景知识和大量的实验[21]，而网格搜索方法容易受到维度约束，搜索范围有限，难以找到最优参数[27]。采用智能优化算法对超参数进行调整不仅能够获得最优参数组合，还可以减少时间，提升效率。

3.2.1 改进的天鹰优化算法 天鹰优化器(Aquila Optimizer，AO)是Abualigah等[22]于2021年提出的一种新型智能优化算法，具有较强的全局搜索能力和较快的收敛速度。天鹰优化算法的灵感来自于天鹰的狩猎行为。天鹰主要有四种狩猎行为，即高空翱翔和垂直俯冲攻击、等高线飞行和短滑翔攻击、低空飞行和慢速下降攻击以及行走攻击并捕获猎物。这四种狩猎行为分别属于扩大搜索、缩小搜索、扩大开发和缩小开发的四个阶段。然而，AO算法采用简单的随机方式对种群初始化，难以保证初始化种群分布的均匀性和多样性，并且在开发阶段容易陷入局部最优。针对上述问题，本文采用混沌理论中搜素速度较快的Tent混沌映射代替传统天鹰优化算法中的随机初始化，以增强种群的均匀性和多样性；然后，引入非线性飞行速率更新策略替代原来的线性飞行速率更新策略，以提高天鹰优化算法跳出局部最优的能力，从而提出改进的天鹰优化(IAO)算法。

Tent混沌映射是一个二维混沌映射，具有均匀的分布函数和良好的相关性。Tent混沌映射将正态分布序列转换为混沌序列，能够增强种群间不同个体之间的联系，增加初始种群整体的随机性，从而提升算法前期的全局搜索能力。采用Tent混沌映射生成混沌序列初始化天鹰位置xi，j的过程如下：

首先，由Tent混沌映射生成混沌序列：

(10)

式中：i=1，2，…，N，N为种群中天鹰的总数；j=1，2，…，D，D为待优化超参数的维数；xi，j为[0，1]内的随机值。

然后，将式(10)中的混沌序列映射到解的搜索空间，得到混沌初始化种群：

(11)

式中LBj和UBj分别为第j维待优化参数取值的下界和上界。

天鹰优化算法的全局搜索能力较强，但其局部开发能力较弱，容易陷入局部最优解而导致寻优精度降低。虽然天鹰优化算法在开发阶段中引入了随机性较强的莱维(Levy)飞行策略，增强了算法跳出局部最优的能力，但是莱维飞行策略在迭代后期容易出现搜索距离过大而导致难以发现全局最优位置的问题。天鹰飞行速率G2是天鹰优化算法在缩小开发阶段中的一个重要参数，对于提高算法优化性能具有重要意义。然而，天鹰飞行速率G2随着迭代次数的增加而呈现线性下降的变化趋势。相关研究[28-30]表明，智能优化算法中的非线性参数对于增强算法全局、局部搜索能力或提高收敛速度具有重要作用。因此，采用非线性飞行速率更新策略对天鹰飞行速率G2进行改进，以弥补算法后期局部搜索能力较弱而使群体陷入早熟的缺陷。改进后的G2可表示为G′2，表达式如下所示：

(12)

式中：t为当前迭代次数；I为最大迭代次数。

种群混沌初始化增强了原算法的全局搜索能力，非线性飞行速率更新策略增强了原算法的局部搜索能力，因此将两者结合起来可以增强天鹰优化算法的整体寻优能力。

3.2.2 IAO-XGBoost集成学习模型实现流程 利用IAO算法的寻优能力和XGBoost算法的学习能力，提出基于IAO算法改进的XGBoost(IAO-XGBoost)集成学习模型，该模型充分通过IAO算法找到XGBoost训练过程中使其预测结果和模拟值之间误差最小时的一组最优参数值，达到改进XGBoost算法预测性能的目的。IAO-XGBoost集成学习算法的实现流程如图2所示。

4 面向大坝渗流性态智能分析的可解释机器学习框架SHAP

对于大坝渗流性态指标预测而言，除了准确性和预测速度之外，了解模型为何会对不同的样本输入特征得出相应的预测结果，关系到模型预测结果的可信度，同样是大坝运行管理人员关心的问题。机器学习算法在进行预测时，其内部运作过程类似于“黑箱”，难以直观地被人类理解，因此有必要对其预测结果进行可解释性分析[31]。在大坝渗流性态预测中，可解释性意味着找出影响大坝渗流性态指标预测的关键特征，阐明模型的决策过程，从而提供大坝运行管理人员可理解的渗流性态指标预测结果。

可解释机器学习是指使机器学习系统的行为和预测对人类可理解的算法或模型[32]。Shapley加性解释(SHapley Additive exPlanation，SHAP)是由Lundberg等[18]提出的一种用于增强机器学习模型可解释性的统一框架，可以对每一个样本的每一个特征变量计算出线性可加的贡献值，从而达到解释的效果[19]。尽管传统的XGBoost算法可以进行特征重要性分析，挖掘影响预测结果的关键特征，但是这只能得出特征的重要程度，难以解释该特征是如何影响预测结果的[17]。与XGBoost算法的特征重要性分析相比，SHAP不仅可以对样本特征的重要性进行排序，挖掘影响预测结果的关键特征，并定性分析样本特征与预测结果的正负相关性，还可以显示出单个样本中各个特征对此样本的预测结果是如何起作用的，显著提高预测结果的可信度[20]。

可解释机器学习框架SHAP的核心在于诺贝尔奖得主Lloyd Shapley提出的Shapley值[33]，该值主要用于解决合作博弈论中的分配均衡问题，即解决如何分配多人合作所创造的总价值的公平分配问题[34]。在机器学习中，可以把输入特征看作合作人员，把模型预测结果看作所创造的总价值，则Shapley值可计算出各特征对模型预测结果的贡献。

假设第i个渗流样本为xi，其第j个特征值xi，j的Shapley值Øxi，j的计算公式如下所示：

(13)

式中：M是渗流数据集中所有特征的集合，其维度为m；S是从M中抽取出来的子集，其大小为|S|；fxi(S)是只使用特征集合S时，模型对渗流样本xi的预测值，当S是空集时，fxi(S)的值称为基础值，相当于模型的预测值在所有渗流样本上的平均值；fxi(S∪{xi，j})是在特征集合S的基础之上，添加特征值xi，j时模型对渗流样本xi的预测值在所有样本中的平均值；M{xi，j}表示M中剔除第j个特征之后的全部特征子集。

基于Shapley值，SHAP对渗流性态指标预测模型的解释可以用一个加性模型表达如下：

(14)

式中：Øxi，0为整个渗流性态指标预测模型输出的基线，即所有训练样本的预测均值；Øxi，j为Shapley值，表示第i个渗流样本的第j个特征对预测模型输出f(xi)的贡献值；zj为简化特征指示系数，取值为0或1，zj=1表示该特征存在于待解释样本xi中；zj=0则表示该特征不存在于xi中。

对于上式中的Shapley值Øxi，j，当Øxi，j>0时，说明第i个渗流样本的第j个特征提升了预测值，对模型输出有正向作用；而当Øxi，j<0时，说明该特征降低了预测值，对模型输出起反向作用。可见，SHAP算法的作用，是与各个特征的贡献值共同将模型的预测结果从基线值推演到最终的模型预测值。

5 案例研究

以我国西南某土石坝工程为研究对象，该土石坝工程为黏土心墙堆石坝，坝基河床覆盖层深厚，根据其物质组成、结构特征、成因和分布情况等可自下而上分为4大层7个亚层，即①漂(块)卵(碎)砾石层、②-1漂(块)卵(碎)砾石层(图3中未切到②-1层)、②-2碎(卵)砾石土层、②-3粉细砂及粉土层、③-1含漂(块)卵(碎)砾石土层、③-2砾石砂层和④漂卵砾石层。所选工程的典型剖面地质图如图3所示，由于③-2层分布范围较小，故将其与③-1层合并为一层(以③层表示)进行研究。

采用基于BLSOGI的多地质体自动建模方法，建立该土石坝工程的坝基地质模型。由于大坝桩号0+80—桩号0+251附近的区域为重点关注区域，故选取该区域作为渗流分析的计算区域，如图4所示。

图4 研究区域地质模型图

在本案例研究中，将坝基防渗帷幕(即图3中的混凝土防渗墙、覆盖层帷幕灌浆和基岩帷幕灌浆)的最大水力梯度作为计算分析的渗流性态指标，将上游水位Hu、下游水位Hd以及坝基覆盖层①层、②-1层、②-2层、②-3层、③层、④层的渗透系数(分别表示为K1、K2、K3、K4、K5、K6)作为坝基防渗帷幕最大水力梯度的影响变量。

5.1 IAO-XGBoost集成学习模型建立与结果分析通过对该工程自2013年5月1日到2021年12月25日的上下游水位监测数据进行统计分析，设置上下游水位的取值范围。将坝基和坝体各区域设置为各向同性的均质多孔介质，其中坝基各覆盖层渗透系数的取值范围如表1所示，坝体各区域及坝基其余地层的渗透系数则根据现场勘探数据和室内试验数据设置。

表1 上下游水位和坝基各覆盖层渗透系数的取值范围

根据表1所示的上下游水位和坝基各覆盖层渗透系数的取值范围，采用最优拉丁超立方抽样方法抽取200组样本点，并将各样本点逐个输入到渗流数值模型中进行模拟计算，从而获得对应的坝基防渗帷幕最大水力梯度值。上下游水位和坝基各覆盖层渗透系数的样本点，与对应的坝基防渗帷幕最大水力梯度模拟值构成样本数据集，用于对坝基防渗帷幕最大水力梯度预测模型进行训练和测试。其中，训练集含有160个样本，测试集含有40个样本。

采用五折交叉验证方法对模型进行训练，XGBoost算法的超参数max_depth、learning_rate和n_estimators通过IAO算法进行寻优，其寻优范围分别为[2，10]、[0.01，1]和[2，100]。在IAO算法中，天鹰种群数设置为20，迭代次数设置为100次，以均方误差(Mean Square Error，MSE)作为适应度函数，则超参数max_depth、learning_rate和n_estimators的寻优结果分别为2、0.2513和54。

在模型训练完成后，以测试集对模型预测性能进行验证。测试集的预测结果如图5所示。从图中可以看出，坝基防渗帷幕最大水力梯度值的预测值与模拟值拟合较好。进一步计算预测结果的误差指标，其决定系数R2、均方根误差RMSE、平均绝对误差MAE和平均绝对百分比误差MAPE分别为0.9303、1.3675、1.0890和1.7030%，表明IAO-XGBoost模型的预测结果较为准确。

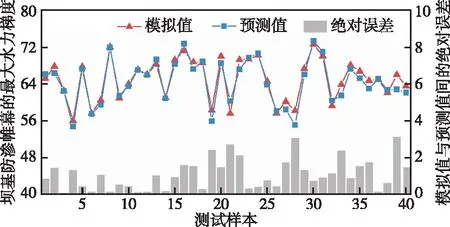
图5 测试集的预测结果图

5.2 模型预测结果解释

5.2.1 样本特征全局影响分析 在基于IAO-XGBoost模型获得坝基防渗帷幕最大水力梯度值的预测结果后，可进一步对输入特征的重要程度进行分析，以挖掘影响模型预测结果的关键特征。本文采用特征平均增益值计算输入特征的重要性评分，则各特征的重要性排序如图6所示。从图中可以看出，上游水位Hu对模型预测结果的影响最大，下游水位Hd次之，渗透系数K4和渗透系数K6的影响也相对较高，而渗透系数K1、K3、K5和K2的影响相对较小。

虽然IAO-XGBoost算法通过特征重要性分析能够获得影响预测结果的关键特征，但是难以判断各输入特征对预测结果的正负影响。将IAO-XGBoost算法与SHAP理论相结合可有效解决这一问题，提高模型的可解释性。

将每个样本的每个特征的Shapley值绘制成散点图，并用颜色的渐变表示特征值的大小关系，如图7所示。在图7中，每个点表示各特征对应样本点的Shapley值，各点的颜色越红表示特征本身的取值越大，而各点的颜色越蓝，则表示特征本身的取值越小；图中x轴表示Shapley值，当特征的Shapley值大于0时，表示该特征对模型预测结果有正影响，当特征的Shapley值小于0时，则表示该特征对模型预测结果有负影响；y轴为各特征，各特征根据其重要性大小从上到下排列。

图7 特征重要性散点图

由图7可知，上游水位Hu、下游水位Hd、渗透系数K4和渗透系数K6对模型预测结果的影响较大。其中，上游水位Hu对于模型预测结果的影响最大，而且当上游水位Hu的值逐步增大时，其对应的Shapley值大于0并且会随着特征值的增大而增大，对模型预测结果的正影响效果较为显著；当上游水位Hu的值逐渐减小时，其对应的Shapley值小于0并且也会随着特征值的减小而减小，对模型预测结果的负影响效果也较强。对于渗透系数K6，当其特征值增大时，其对应的Shapley值大于0，但Shapley值增大幅度较小，表示对模型预测结果的正影响效果不明显；当渗透系数K6的特征值减小时，其对应的Shapley值小于0并且对应的Shapley值也在减小，则对模型预测结果产生负影响。与其他特征有所不同，下游水位Hd、渗透系数K4和K1的特征值增大时，其Shapley值小于0且对应的Shapley值也在减小，对模型预测结果有负影响；当其特征值减小时，其Shapley值大于0，则对模型预测结果有正影响，但该特征对模型预测结果的正影响没有负影响明显。

SHAP理论也可对特征重要性进行度量，将每个特征的Shapley值绝对值的平均值作为该特征的重要性度量标准，其值越大，则表明该特征越为重要，如图8所示。由图8可知，上游水位Hu对应的值最大，则表明该特征在模型中最重要，对模型预测结果的贡献最大，然后依次是下游水位Hd、渗透系数K4和K6对模型预测结果影响较大。由于特征重要性的度量标准不同，故基于SHAP理论的特征重要性排序结果与基于IAO-XGBoost算法的特征重要性排序结果(图6)并不完全相同。但在图8的特征重要性排序中，仅渗透系数K5和渗透系数K3的排序结果与IAO-XGBoost算法(图6)的排序结果不同，其他特征均与图6中的排序结果相同。

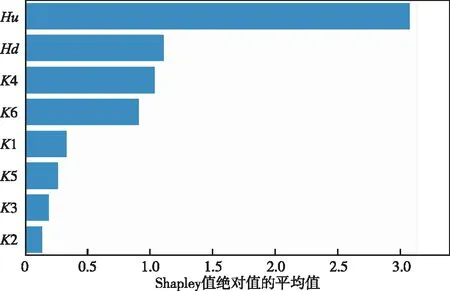
图8 基于SHAP理论的特征重要性排序

5.2.2 特征交互影响分析 两个输入特征对模型预测结果的交互影响可通过图9所示的SHAP依赖图可视化。图9中横轴表示某一输入特征的特征值，左纵轴表示该输入特征对应的Shapley值，右纵轴为以颜色标识的另一输入特征的特征值，颜色由蓝色至黄色表示输入特征的特征值由低到高。

图9 特征对模型预测结果的交互影响分析

以渗透系数K3和K4的交互影响作用为例(即图9(c)与图9(d))进行说明。如图9(c)，对于渗透系数K3而言，渗透系数K3的值越大使得模型预测结果值减小，当渗透系数K3的值小于0.00225 cm/s左右时，其绝大部分Shapley值大于0，则对模型预测结果值有正影响；当渗透系数K3的值大于0.00225 cm/s左右时，其Shapley值小于0，则对模型预测结果值有负影响。如图9(d)，对于渗透系数K4而言，渗透系数K4的值越大同样使得模型预测结果值减小，当渗透系数K4的值小于0.0005 cm/s左右时，其绝大部分Shapley值大于0，则对模型预测结果值有正影响；当渗透系数K4的值大于0.0005 cm/s左右时，其Shapley值小于0，则对模型预测结果值有负影响。综合渗透系数K4和K3分析可发现，当渗透系数K3的值小于0.00225 cm/s时，渗透系数K4越大，渗透系数K3对模型预测结果的正影响越大，而当渗透系数K3的值大于0.00225 cm/s时，渗透系数K4越大，渗透系数K3对模型预测结果的负影响越大；当渗透系数K4的值小于0.0005 cm/s时，渗透系数K3越大，渗透系数K4对模型预测结果的正影响越大，而当渗透系数K4的值大于0.0005 cm/s时，渗透系数K3越大，渗透系数K4对模型预测结果的负影响越大。

5.2.3 单个样本特征影响分析 从测试集中挑选两个预测样本，采用SHAP理论解释输入特征对样本预测结果的影响，如图10所示。图中横坐标为预测值的大小，纵坐标为输入特征的数值，红色表示输入特征的Shapley值为正，蓝色表示输入特征的Shapley值为负；且红色和蓝色区域的面积越大，表示Shapley值越大，则对样本预测结果的影响也越大。

图10 样本预测图

以图10(a)为例进行说明。在图10(a)中，输入特征对样本6的预测结果影响从大到小分别为上游水位Hu、渗透系数K6、下游水位Hd、渗透系数K1、渗透系数K4、渗透系数K2、渗透系数K5和渗透系数K3。其中，上游水位Hu在样本6中的特征值为1369.762 m，Shapley值为-3.74，表明上游水位Hu对此样本的预测值产生负影响；渗透系数K6在此样本中的特征值为0.013 cm/s，它的Shapley值为-2.15，表明渗透系数K6对此样本的预测值同样产生负影响。同理，下游水位Hd的样本特征值为1303.556 m，Shapley值为+1.01，则下游水位Hd对样本6的预测值产生正影响。坝基防渗帷幕最大水力梯度预测模型输出的基线为64.854，在图10(a)中各个特征的共同作用下，样本6的最终预测值为59.465。

此外，从图10中两个不同样本的预测图可以看出，同一输入特征对不同样本的预测影响存在差异，故对输入特征的解释分析不能太过绝对，以免产生误判[19]。

5.3 对比分析与讨论基于测试集数据，采用决定系数R2、均方根误差RMSE、平均绝对误差MAE和平均绝对百分比误差MAPE四种误差指标对IAO-XGBoost与梯度提升决策树(Gradient Boosting Decision Tree，GBDT)、随机森林(Random Forest，RF)、决策树(Decision Tree，DT)和支持向量回归(Support Vector Regression，SVR)四种算法的预测性能进行对比分析，如图11所示。其中，GBDT、RF、DT和SVR的超参数都通过IAO算法寻优而得，故在图11中分别表示为IAO-GBDT、IAO-RF、IAO-DT和IAO-SVR。

图11 误差指标计算结果

从图11可以看出，相比于其余四种算法，IAO-XGBoost集成学习算法具有最高的R2值，而其RMSE、MAE和MAPE值均较小，表明IAO-XGBoost算法的预测精度较高。通过进一步计算可知，与IAO-GBDT、IAO-RF、IAO-DT和IAO-SVR算法相比，IAO-XGBoost算法的预测精度分别提高了0.52%、11.64%、37.21%和25.07%。相比于IAO-XGBoost算法，IAO-GBDT和IAO-RF的预测精度较低，这是由于XGBoost模型通过引入损失函数的二阶泰勒展开和正则项，优化了模型复杂度，避免了模型过拟合，从而提高了模型预测精度。此外，IAO-DT和IAO-SVR的预测精度均低于IAO-GBDT和IAO-RF的预测精度，这是由于IAO-DT和IAO-SVR属于单一的机器学习算法，而IAO-GBDT和IAO-RF均属于集成学习算法，具有更好的预测性能和泛化能力。

IAO-GBDT和IAO-RF这两种算法也能够通过特征重要性分析，得出影响预测结果的关键输入特征，因而也具有一定的模型可解释性。IAO-GBDT和IAO-RF的特征重要性排序结果如图12所示。将图12与IAO-XGBoost和SHAP理论的特征重要性排序结果(如图6和图8)进行对比分析，可以看出，这四种算法所得的特征重要性排序并不完全相同，但是对坝基防渗帷幕最大水力梯度预测结果影响最大的输入特征均为上游水位Hu，且下游水位Hd、渗透系数K4和渗透系数K6均对模型预测结果具有较大影响。此外，IAO-XGBoost、IAO-GBDT和IAO-RF这三种算法只能用于样本输入特征的全局解释，而SHAP理论还能在全局解释中发现输入特征与坝基防渗帷幕最大水力梯度预测值的正负相关趋势，并且能够将同一个输入特征在不同样本之间进行比较，提供模型预测结果的局部解释，因而SHAP理论具有更强的模型可解释性。

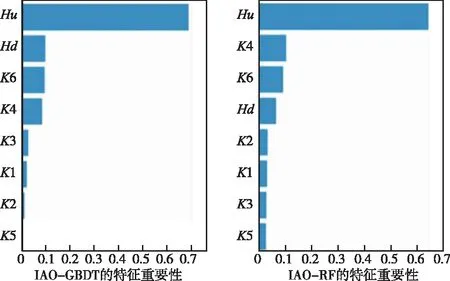
图12 IAO-GBDT和IAO-RF的特征重要性排序

6 结论

本文建立了土石坝渗流性态分析的IAO-XGBoost集成学习模型，并基于SHAP理论对预测结果进行解释，最后通过案例研究和对比分析，验证了所提方法的有效性。所得主要结论如下：

(1)在采用多地质体自动建模方法和CFD技术对土石坝渗流场进行数值模拟的基础上，提出了基于IAO-XGBoost集成学习的渗流性态指标预测方法，采用基于混沌初始化和非线性飞行速率更新策略改进的天鹰优化(IAO)算法对 XGBoost 集成学习算法的超参数进行优化，实现了大坝渗流性态指标的高精度预测，并显著提高了大坝渗流性态分析的效率。

(2)将可解释机器学习框架SHAP理论与IAO-XGBoost集成学习算法相结合，挖掘了影响大坝渗流性态指标预测结果的关键特征，并分析了单个样本的特征对预测结果的影响，增强了IAO-XGBoost集成学习算法的可解释性，从而提高了大坝渗流性态指标预测结果的可信度。

(3)案例分析表明，IAO-XGBoost集成学习算法具有较高的预测精度，相比于IAO-GBDT、IAO-RF、IAO-DT和IAO-SVR算法，其预测精度分别提高了0.52%、11.64%、37.21%和25.07%；通过可解释机器学习框架SHAP理论，得出上游水位Hu和下游水位Hd是影响坝基防渗帷幕最大水力梯度预测结果的关键因素；并且相比于IAO-XGBoost、IAO-GBDT和IAO-RF算法的特征重要性分析方法，SHAP理论不仅能够挖掘影响坝基帷幕最大水力梯度预测结果的关键特征，并在全局解释中发现输入特征与预测结果的正负相关趋势以及特征间的交互影响，而且能够将同一个输入特征在不同样本之间进行比较分析，提供模型预测结果的局部解释，具有更强的模型可解释性。