基于马斯京根参数K、X的等效河道计算方法研究

王船海，俞 悦，吴金宁，陈 钢，马腾飞，曾贤敏

(1.河海大学 水文水资源学院，江苏 南京 210098；2.河海大学 水文水资源国家重点实验室，江苏 南京 210098；3.江苏省水文水资源勘测局常州分局，江苏 常州 213022)

1 研究背景

河道汇流演算属于水力学问题[1]，但由于对河道实测断面资料的要求高、计算耗时长等问题，水文学家们研究和发展了一系列的水文学方法和简化的水动力学方法来进行演算[2-3]。马斯京根法便是最经典的水文学方法之一。水动力学方法[4-6]则主要是通过求解圣维南方程组，但由于圣维南方程组属于复杂的偏微分方程，求解过程较为复杂[7-8]。从首次面世以来，马斯京根法经历了从经验性方法上升为具有物理基础方法的发展历程[9]。在长期发展的过程中，研究者们在传统线性方法的基础上，发展出一系列的非线性方法，如马斯京根-康吉法[10]、可变参数马斯京根-康吉法[11]等。马斯京根法计算过程简便，所需资料少，且精度能满足一般科研、工程需求。目前，马斯京根法在我国已经取得了广泛应用，利用马斯京根法进行汇流演算的成果非常丰富[12-14]。同时，经过广大学者的不断探索，对圣维南方程组进行求解的水动力学模型发展已经日趋成熟，能够快速有效地模拟河道流量、水位、流速等要素。

“等效河道”是一种将复杂的实际河流简化为具有相似水动力特性的“理想河道”的概念，能够将复杂的自然河道形态简化为等效的理想河道形状和参数，与原河道具有相似的水动力特性的虚拟河道。早在1988年Chow等[15]就已提出了等效河道的概念，然而由于河道水力特性复杂，等效的河道需要考虑的要素过多。目前国内外对等效河道的研究较少，高学平等[16]通过在河道内分区设置植物，对含植物河道等效创面阻力进行了试验性研究；龚定等[1]根据原河道大断面形状对河道断面进行了梯形概化。可以看出，关于等效河道的研究大部分是采取的试验性研究，或是对河道断面直接进行简单概化处理，而通过简便的参数实现等效河道的公式推导的研究基本没有。

随着国家数字孪生流域建设中“四预”的新要求，对洪水预报提出了新的挑战，包括预报河道水位、流速等信息。目前，对马斯京根法的相关研究大多聚集在对K和X参数值更精确的获取[17-18]，以及马斯京根法演算结果精度的进一步提高中[19-21]。传统的马斯京根法输出结果类型单一，对河道内其他要素的获取需更多资料支撑，无法与水动力模型相结合进行运用。因此，本文提出了一种基于马斯京根参数K、X的等效河道计算方法，通过构建等效河道，可求解出资料缺乏地区河道的河宽、河道比降、最大水深信息，通过水动力模型进行演算后实现了河道水位、流速、流量等要素的模拟。

2 计算原理

2.1 传统马斯京根法水量平衡方程与槽蓄方程联立：

(1)

得：

Q2=C0·I2+C1·I1+C2·Q1

(2)

其中：

式中：I0为上断面流量，I1、I2分别为时段始末上断面流量，m3/s；Q0为下断面流量，Q1、Q2分别为时段始末下断面流量，m3/s；W0为河段槽蓄量，W1、W2分别为时段始末河段槽蓄量，m3；Δt为计算时段；K和X为马斯京根法主要参数。K为蓄量常数，表示稳定流时河段的传播时间，随流量的变化而变化；X为楔蓄系数，由河道楔蓄因素和调蓄因素组成。

X的计算公式如下：

(3)

式中：l为特征河长，m；L为总河段长，m。

2.2 总河段K总、X总与分河段Ki、Xi关系如图1所示，将一个长河段分为N个子河段，建立马斯京根法总河段K总、X总与分河段Ki、Xi关系。

图1 马斯京根分河段示意

(4)

(5)

假设每个分河段的K1=K2=…=KN，X1=X2=…=XN，则：

(6)

式中：K总、X总为马斯京根总河段参数；Ki、Xi为马斯京根分河段参数。

2.3Ki、Xi与水动力模型河道要素转换关系结合特征河长，利用马斯京根法分河段参数Ki、Xi建立等效河道要素的转换关系。

已知曼宁公式：

(7)

波速-河长传播时间关系式：

Li=Cs·Ki=Ki·αu

(8)

特征河长计算公式：

(9)

令水力半径R=R(H)，联立式(7)(8)，得到水力半径R、河道比降i0与马斯京根法分河段参数Ki之间的关系：

(10)

断面面积A=f(H)。将曼宁公式与流量公式(Q=f(H)·u)联立，得洪峰流量Q的表达式：

(11)

对式(11)中的H偏导得：

(12)

通过联立式(3)和式(9)，构建等效河道。

将式(12)代入式(9)，得：

(13)

联立式(3)与式(13)，得：

(14)

建立河道比降i0与马斯京根参数之间的关系。由式(11)得到以下变形：

(15)

将式(15)代入式(14)得：

(16)

由式(10)、式(11)、式(16)得到通用断面形状的马斯京根法参数Ki、Xi与等效河道要素之间的转换关系。

3 具体河道断面计算方法

3.1 矩形断面如图2所示，假设河道断面形状为矩形时，经简化，水力半径Rr=Hr，断面面积f(H)r=Br·Hr，f′(H)r=Br，代入式(16)得河道比降i0r：

i0r=Dr·Hr

(17)

图2 矩形断面示意

式中：

(18)

将i0r=Dr·Hr带入式(10)，得断面最大水深Hr：

(19)

由式(11)得河宽Br：

(20)

由式(17)(19)(20)得到矩形断面的马斯京根法分河段参数Ki、Xi与水动力模型河宽Br、河道比降i0r、最大水深Hr之间的转换关系。

图3 抛物线型断面示意

(21)

代入式(16)得河道比降i0p：

i0p=Dp·Hp

(22)

式中：

(23)

将i0p=Dp·Hp带入式(10)，得断面最大水深Hp：

(24)

由式(11)得β的计算公式：

(25)

则河宽Bp：

(26)

由式(22)(24)(26)得到抛物线型断面的马斯京根法分河段参数Ki、Xi与水动力模型河宽Bp、河道比降i0p、最大水深Hp之间的转换关系。

根据Ki、Xi与等效河道要素的转换关系，通过马斯京根参数Ki、Xi、总河段长L、洪峰流量Q、糙率n、平均流速转换波速系数α及分河段数N，可以计算得到不同概化断面下等效河道的河宽B、河道比降i0、最大水深H等河道信息。本文只提出了抛物线型和矩形这两种概化断面下的转换关系，根据相同的原理，其他形状的概化断面(如三角形、梯形等)也可推导求出。

4 基于K、X等效河道的具体应用及合理性分析

4.1 基于K、X等效河道的具体应用何惠等[22]提出了用最小二乘法对马斯京根法的K、X参数进行最优估计，并以1961年海河流域南运河称沟湾至临清段的一次洪水过程为例，其中K=13.05、X=-0.2716。现以该方法率定的K、X值运用于本文提出的等效河道方法，对该场次洪水进行演算。

南运河位于河北省南部，南运河称沟湾至临清段全长83.8 km，如图4(a)所示。本文提出的等效河道方法对该河段的概化如图4(b)(c)所示。整个河道概化为一条长83.8 km的长河段，取N为100，将河段等距离划分为100个子河段，取糙率n为0.02，洪峰流量Q为550 m3/s。经计算，当河道断面概化为矩形时，河道全程比降为0.0045%，河宽为36.04 m；当河道断面概化为抛物线型时，河道全程比降为0.0042%，河宽为51.62 m。K、X值对应的等效河道信息，转换后可用于水动力模型的边界条件。由临清断面形状信息，结合曼宁公式及流速流量关系可推出临清断面水位流量关系。取南运河称沟湾实测流量为上边界条件，临清断面的水位流量关系为下边界条件进行模拟。

图4 实际河道及下边界水位流量关系

图5和表1为出口临清断面实测流量、参考文献[22]方法演算流量及本文方法演算流量对比。从表1统计结果来看，矩形断面下，均方根误差RMSE为10.71，比文献方法大4.64；可决系数R2为0.99，与文献方法相近，均在0.99 以上。抛物线型断面下，均方根误差RMSE为10.76，比文献方法大4.69；可决系数R2为0.99，与文献方法相近，均在0.99 以上。本算例下，两种概化方式演算结果相差不大，矩形的概化方式表现更好。从图5流量过程线来看，本文提出的两种概化方法演算的临清流量结果较好，与文献[22]方法演算结果相差不大，能反应临清出流过程。

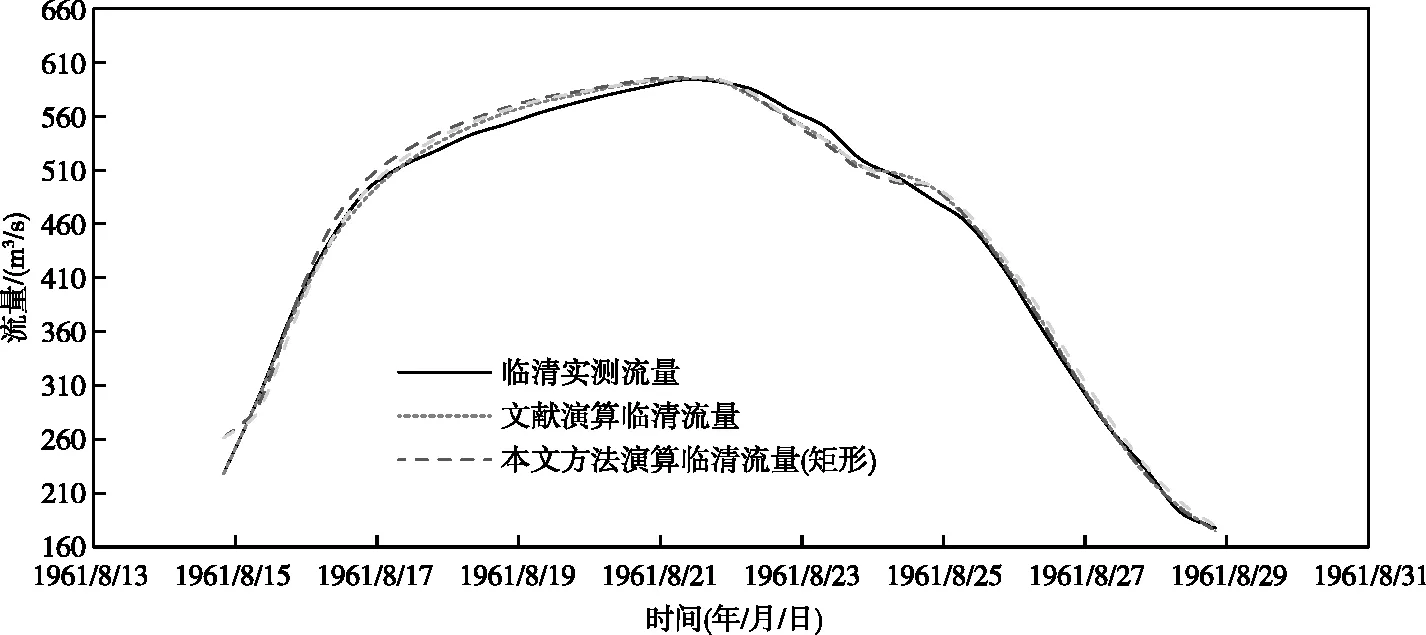
图5 称沟湾—临清流量过程线(1961年)

表1 秤钩湾—临清流量计算结果对比

本文方法演算出不同断面处的流速情况对比如图6，可以看到，两种概化方式下，临清断面处流速情况与图5中的流量过程线一致，计算结果具有可靠性。由图6中不同断面的流速情况可以看出，矩形断面下，各断面流速于8月21日达到最大，其中临清断面流速为1.6 m/s。同时，抛物线型断面下，各断面在8月22日达到最大流速，其中临清处流速最大，为1.37 m/s。

图6 不同等效河道断面处流速情况

4.2 合理性分析本文提出的方法使用的是洪峰流量，而非入流过程，不同流量下相应的河道概化断面也会出现偏差，选用洪峰流量进行演算，是考虑到洪峰流量是最值得关注的特殊情况。因此，不同入流及时间变化都是非线性分析的重要考虑因素。从表2和图7可知，当输入的洪峰流量分别为200，400，600 m3/s，概化断面为抛物线型时，3种拟合效果均较好，R2均趋于1，且RMSE均小于16。但不同的洪峰流量在计算得到的洪水涨落过程也呈现出一定的差异性，体现了非线性的特征。从这三种计算结果来看，当洪峰流量为400 m3/s时，误差最小。

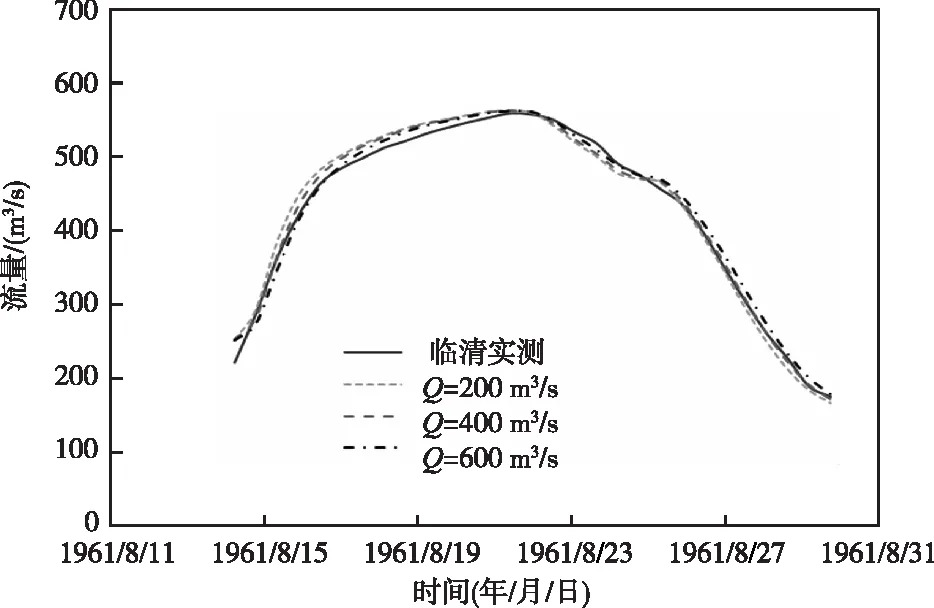
图7 不同洪峰流量对应的模拟结果

表2 不同洪峰流量Q下计算流量结果对比

为了进一步验证本文方法计算水位、流速等信息的准确及合理性，将本文提出的两种概化河道计算出的结果与临清断面实测日平均水位进行对比。如表3所示，矩形断面下，均方根误差RMSE为0.90，可决系数R2为0.97；抛物线型断面下，均方根误差RMSE为0.95，可决系数R2为0.95。如图8所示，本文提出的两种概化方式均能在一定程度上反应水位的变化情况，趋势一致。

图8 临清断面实测水位与计算水位对比

表3 临清断面水位计算结果对比

计算不同洪峰流量下，两种河道断面概化方式对水位的计算结果如表4和图9所示。可以看到，不同的洪峰流量对水位的计算结果呈现出一定的非线性特征，但从RMSE和R2这两个指标来看，模拟结果表现优秀，RMSE均小于1.4，R2均趋于1。从水位过程线中可以清晰的看出，不同洪峰流量下，演算得出的结果差异较小。总的来看，相较于抛物线型断面，矩形断面计算结果更优。

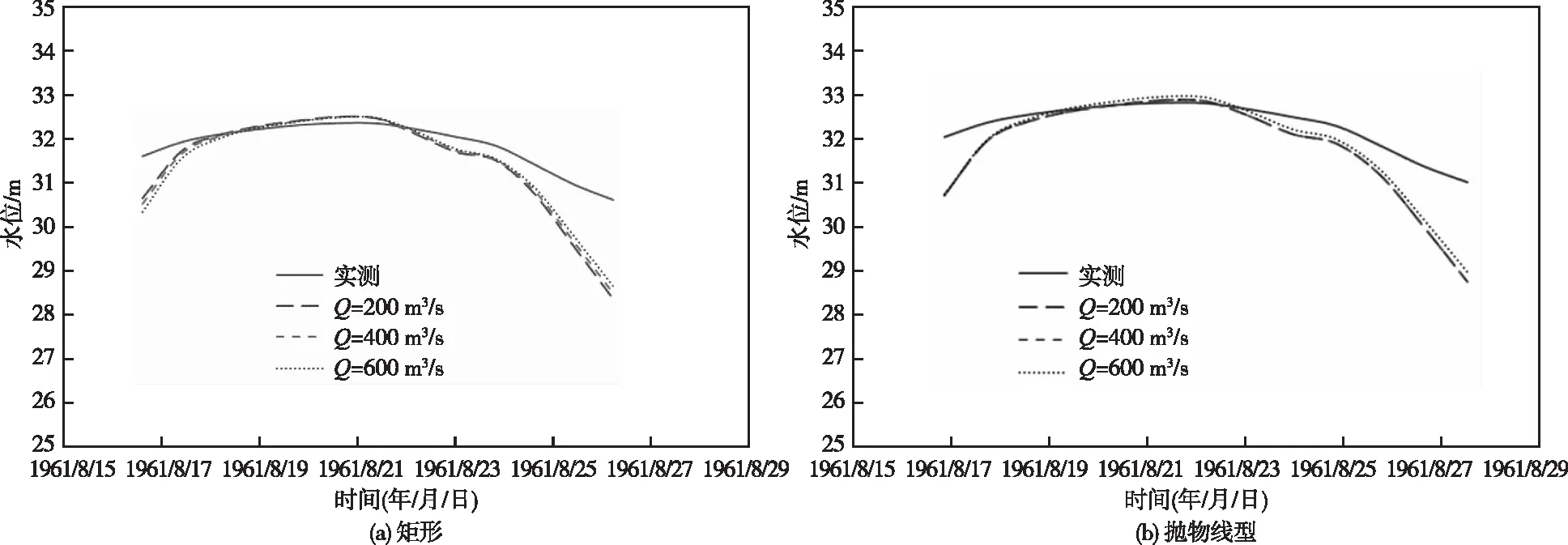
图9 不同洪峰流量下临清断面实测水位与计算水位过程

表4 不同洪峰流量下临清断面实测水位与计算水位结果对比

实测的河道大断面资料如图10所示，可以看到，称沟湾测站过水断面形状较不规则，主槽间距为52.78 m。在最大水位为41.18 m时，本文方法概化的矩形河道断面河宽36.04 m，抛物线型河道断面河宽44.67 m。可以看到，这两种概化方式都十分对称，是一种理想化的河道概化方式，且大致能够描述河道断面。值得一提的是，本文提出的概化河道与实测大断面仍存在一定差距，这主要由于本文提出的概化方法使整个河道每个断面都均化为唯一的断面形状，称沟湾断面只是其中一个断面，因此存在一定差距是合理的现象。

图10 称沟湾站实测大断面形状与概化断面对比

5 结论

本文提出了基于K、X等效河道的计算方法，通过马斯京根法中参数K、X构建等效河道，推演出不同的概化河道断面(矩形、抛物线型)下的河宽、河道比降和最大水深计算公式，并根据参考文献中率定好的参数在实例中进行验证。结果表明，该方法在传统马斯京根法的基础上，通过上断面流量、马法参数K、X值、河道长度L、糙率n、平均流速转换波速系数α和洪峰流量Q，就可以推演出概化河道断面的河宽B、河道比降i0和最大水深H推导公式。利用这些信息，除了可以通过水动力学的方法对资料缺乏地区的河道进行流量预报外，在进一步的应用中，任意时刻、河道任意断面水深、流速信息也能在水动力模型中模拟出来。总体来说，本研究实现了河道大断面资料的扩充，改进了传统的水文学河道汇流计算模式，有利于实现河道水位、流速过程模拟，为传统的马斯京根法转换为水动力模型计算提供了新方法，具有物理意义明确、计算方法简便、计算精度高等优点。

值得注意的是，传统的马斯京根法的分河段是为了解决长河段下出现的非线性的问题，而本文提出的分河段则是转换后用于水动力模型计算的，N可以为任意值。本研究主要提出的是线性马斯京根法下的等效河道概化方法，但由于实际河道水力要素复杂，往往都会或多或少的受到非线性因素的影响，K、X参数的值会随着Q的变化而变化，因此非线性马斯京根法转换为等效河道的方法也值得研究，以进一步减小计算误差，并缩小概化断面形状与实测断面形状之间的差距。