全局与瞬时特性兼优的燃料电池有轨电车能量管理策略

高锋阳 高翾宇 张浩然 杨凯文 宋志翔

（兰州交通大学自动化与电气工程学院 兰州 730070）

0 引言

大力发展资源节约型、环境友好型的城市轨道交通车辆，缓解传统燃油汽车带给地面公共交通的拥堵、环境污染等压力，已成为实现城市双碳目标的必由之路。传统城市轨道交通牵引供电需架设复杂的接触网，严重影响了城市景观和规划，同时会对电网供给造成较大压力[1]。采用新兴绿色能源取代传统燃煤发电路径为机车供能具有体积小、噪声低、能量转换率高和维护组装方便等显著优势，对深度降碳有突出贡献。其中氢燃料电池是实现零碳排放的关键载体，但在应用到轨道交通运行时存在动态响应慢、无法实现再生制动能量回收等问题[2]，因此，与具有高功率密度优势的超级电容相结合，构建有轨电车新型混合动力系统，已成为电车无电弓受流的理想方案。

然而，城市轨道交通行驶工况具有负荷空间分布广泛、冲击性强以及强脉动、宽频域变化等特性。在上述约束条件下，燃料电池混合动力系统能量管理趋于复杂化的问题制约了其在大功率应用场合的商业和产业化进程。现有动态功率分配策略的实现方式主要可分为经典规则控制和现代优化控制[3]。其中前者逻辑简单，易于实现，但制定规则的过程过于依赖专家经验，且没有考虑与动力系统之间的耦合关系。文献[4]根据需求功率、运行速度和锂电池荷电状态（State of Charge, SOC）等参数制定八种电车自适应运行模式以调节各能量源理想工作点，虽然能够稳定母线电压，但未明确指出优化目标；文献[5]通过识别行驶工况最佳混合度以确定模糊控制的隶属度函数中心和宽度，虽然运行经济性和效率均有所提升，但易于陷入局部最优。文献[6]引入频率解耦策略，通过小波和傅里叶变换对需求功率进行滤波，使主动力源和辅助动力源分别承担平均和峰值负载，有效地缓解了燃料电池负载压力，但目前城市轨道交通领域以低频应用为主，其适用性有待商榷。基于优化的控制方法通过对工程问题进行函数化建模，实现对优化目标的定量求解。其中基于瞬态的优化目标函数单一、求解简单、实时性好，但无法实现全局最优。文献[7]在未知行驶工况条件下，依据锂电池充放电效率所对应的能量等效因子求解系统等效氢耗最小化函数，显著提高了燃料经济性，但缺陷是目标函数应对负载突变的抗干扰能力差。文献[8]将模型预测控制引入混合动力系统的动态功率分配中，在循环工况的预测区域内实现了运营成本局部最优，但对模型精度要求高，计算量大，难以应用于工程实际。文献[9]将神经网络自学习功能与H 无穷控制相结合，解决了车载复合电源这一非线性系统的建模复杂问题，但易于陷入维数灾难。

相较于瞬时优化，全局优化策略能够精细化地解决多个非线性目标函数的协同优化问题，实现多重全局最优。其中具有前沿性的方法主要有动态规划[10-11]、遗传算法[12-13]和庞特里亚金极小值原理（Pontryagin’s Minimum Principle, PMP）[1,14]等。文献[15]将应用于插电式混合动力汽车的PMP 策略与动态规划方法进行了比较研究，前者计算耗时短，便于在线控制，但燃油消耗量较高。文献[16]在机车用燃料电池混合动力系统的在线运行中，将PMP 策略与等效氢耗最小策略（Equivalent Consumption Minimization Strategy, ECMS）进行对比研究，结果表明采用PMP 策略，氢气消耗更少、整体效率更高，但实时性与工况适应性相对较差。

综上所述，为使有轨电车用燃料电池混合动力系统运行兼具全局与瞬时最优特性，提出一种PMP与实时工况构建相结合的应对策略。首先，依据极小值原理推导混动系统运行总氢耗量最小化目标函数，离线求解全局最优燃料电池参考功率；其次，根据电车运行特性划分行驶模式，并基于马尔科夫链分别构建对应的状态转移概率矩阵，进而在线更新瞬时最优的功率分配；最后，对本文所提策略、传统全局PMP 以及瞬时ECMS 策略进行对比研究，验证所提策略的有效性和优越性。

1 混合动力系统组成及布局优化设计

新型供电制式混合动力有轨电车能量系统包括质子交换膜燃料电池发电系统，以及与之配套的大容量制动能量回收储能系统（包括超级电容组与制动电阻）。编组采用两动一拖方案，基于模块化原则进行车顶布局优化设计，其中燃料电池电堆组模块及相应的单向直流变换器模块对称布置于中间车位置的拖车车顶，并辅以散热器和储氢罐模块，便于管路布线；位于头车位置的两个动车车顶均布置一套超级电容组储能模块，并辅以水冷箱和制动电阻模块；同时变频调速模块与车载空调模块对称布置于储能系统模块两侧，便于满足体积空间要求以及提高乘坐舒适度与满意度。

基于Simpowersystem 平台搭建主动式拓扑结构，有轨电车复合供电系统拓扑如图1 所示。

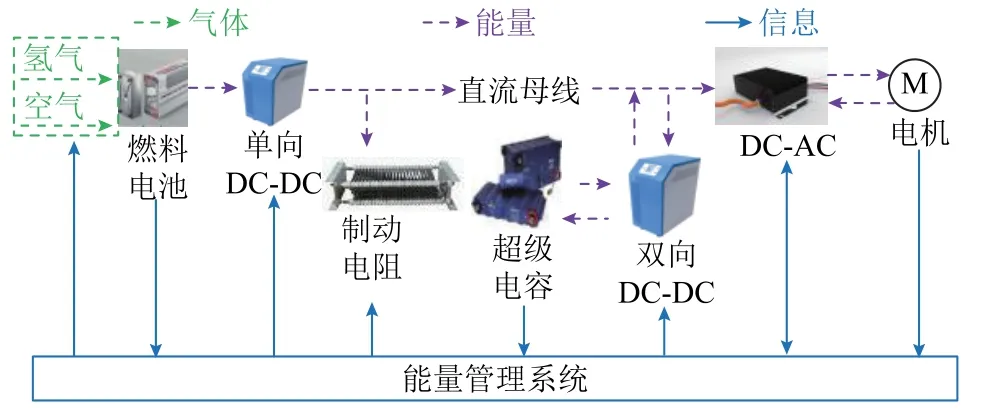
图1 有轨电车复合供电系统拓扑Fig.1 Topological diagram of tram power supply system

考虑到燃料电池无法回收制动能量及超级电容的“削峰填谷”等能量流特性，分别采用单向和双向变流器将主动力源和储能系统连接到直流母线上。依据整车核心技术指标（见表1）制定各部分配置方案：

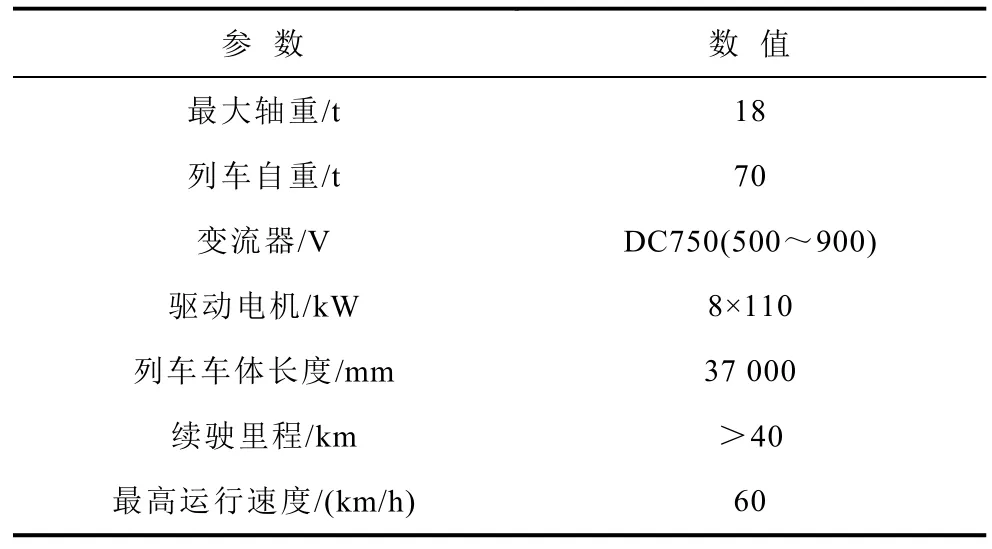
表1 有轨电车主要技术参数Tab.1 Main technical parameters of tram

1）2 套额定功率150 kW，氢气储存量14 kg 的Hydrogenics 型质子交换膜燃料电池堆模块。

2）1 套配置为528 V、45 F 的HCCCAP 型超级电容组。

3）1 套带变压器隔离的单向300 kW 燃料电池DC-DC 变换器，转换器输出电压受输入电流限制。

4）1 套超级电容双向DC-DC 变换器，作为充电机对超级电容充电时输出电压范围为 200～528V，作为供电电源对外放电时输出电压范围为750(1±5%)V。

5）1 套300 kV·A、750 V 输入，200 V、400 Hz输出的逆变器系统。

6）1 套三相可编程DC-AC 负载，模拟列车工况。

7）1 套300 kW 制动电阻，避免超级电容过度充电，当制动功率超出超级电容回收制动能量的能力时，使用电阻器吸收额外的功率。

8）1 套NI PXI-8108 动力总成控制设备。

1.1 燃料电池模型

在氢燃料电池产业应用层面中，稳态数学模型已有大量深入研究，机理相对成熟。然而输出特性无法体现燃料电池在车辆快速启动、急加速和爬陡坡时的参数摄动，进而导致动态响应精度较低。针对这一典型复杂时变非线性系统，搭建简化动态参数耦合等效电路模型，如图2 所示。

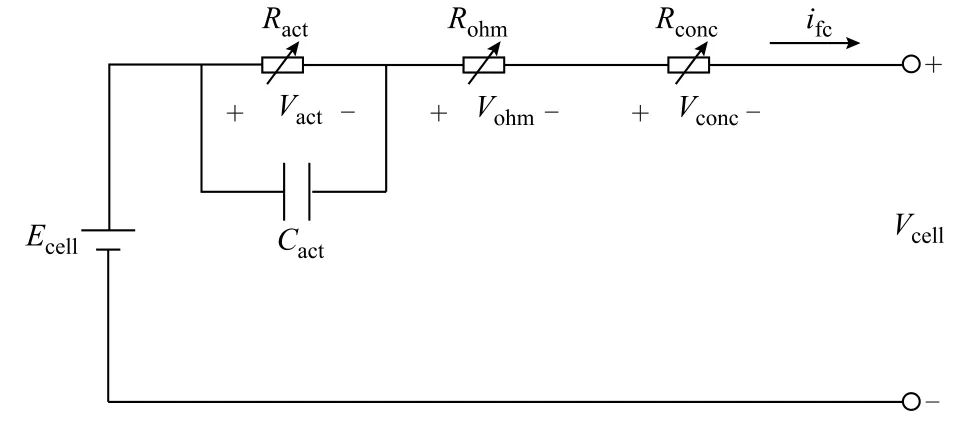
图2 燃料电池模型Fig.2 Model of fuel cell stack

燃料电池电堆输出电压Vfc为

式中，Ncell为单体数量；Vcell为单体端电压。

式中，Ecell为能斯特电压；Virrev为不可逆电压；Vact为激活电压；Vohm为欧姆电压；Vconc为反应物浓度电压。

为验证稳态和瞬态输出特性，将燃料电池数据代入上述模型，空载启动后连接至可编程负载（见图3），电流由零逐渐增大至最大允许值进行仿真极化测试，得到燃料电池电堆端电压、输出功率测试曲线。将其与Plug-Power 公司提供的同一额定条件下（Pfuel=0.116 MPa，Pair=0.1MPa，T=45℃）的工程实际数据进行对比，测试结果如图4 所示。由图4 中可以看出，两曲线稳态、瞬态波动幅值和范围基本吻合，由此表明所提动态参数耦合等效电路模型能够准确地描述氢燃料电池的动、静态外特性。

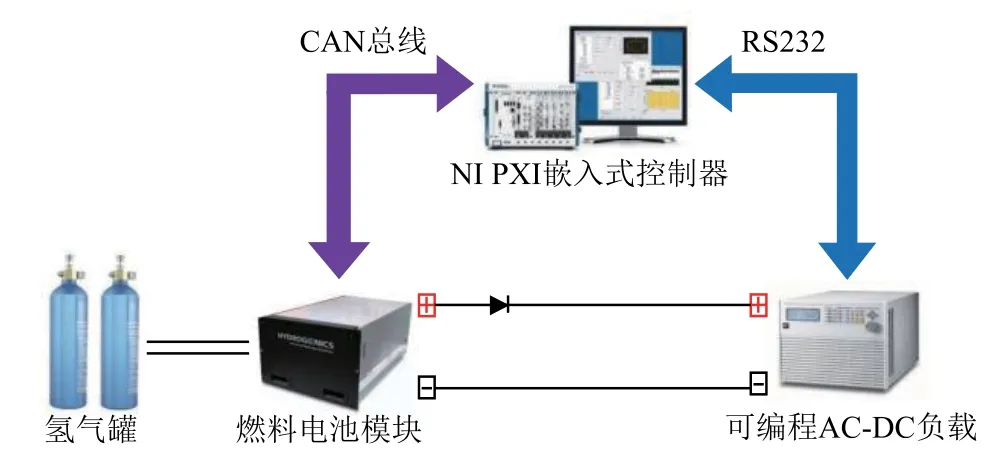
图3 燃料电池极化测试原理图Fig.3 Schematic diagram of fuel cell polarization test

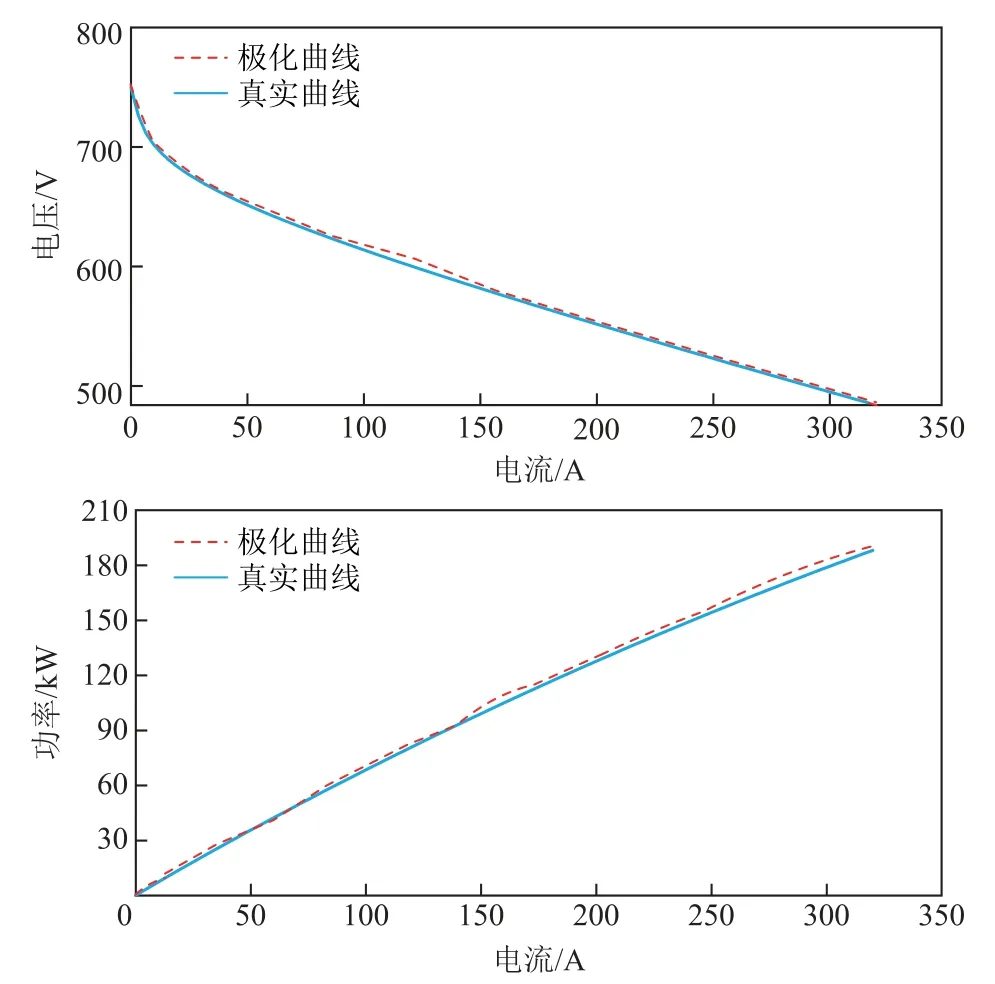
图4 所提燃料电池模型极化测试结果Fig.4 Polarization test results of the proposed fuel cell model

1.2 超级电容模型

超级电容相较于传统静电和电解电容，优势在于可以快速存储或释放高功率密度能量，且响应速度卓越。目前模型构建方法主要可分为时域和频域分析法[17]，但时域分析无法适应轨道交通运行工况中大量新型电气化负荷的强脉动、宽频域变化、冲击性强等特性。基于上述分析，搭建超级电容等效电路模型，如图5 所示。

图5 超级电容模型Fig.5 Supercapacitor model

模型中VT表示超级电容单体端电压，单体电容C为

其中

式中，CH和CGC分别为Helmholtz 和Gouy-Chapman电容；Ne、ε、ε0、Ai、d、CQ、c分别为双层电容组电极层数、电解质材料介电常数、真空介电常数、界面面积、霍兹层宽度、单体电荷数、摩尔常数。

由NS个单体串联和Np个单体并联后组成超级电容组的电容值为

在考虑电阻损耗的情况下，超级电容组输出电压Vsc为

其中

式中，QT为超级电容组极板总电荷；Rsc和isc分别为双层超级电容组等效内阻和瞬态电流。

为检验模型端电压特性，分别在不同充电倍率下对所提模型单体进行极化测试，并在相同条件下将测试曲线与HCCCAP 型超级电容单体数据进行对比，结果如图6a 所示。在每一时刻取各充电倍率下所提模型与HCCCPA 型超级电容端电压最大误差值，结果如图6b 所示。从图6 中可以看出，稳态误差在±0.1 V 以内，表明此模型能够以较高精度推演超级电容的电压行为。

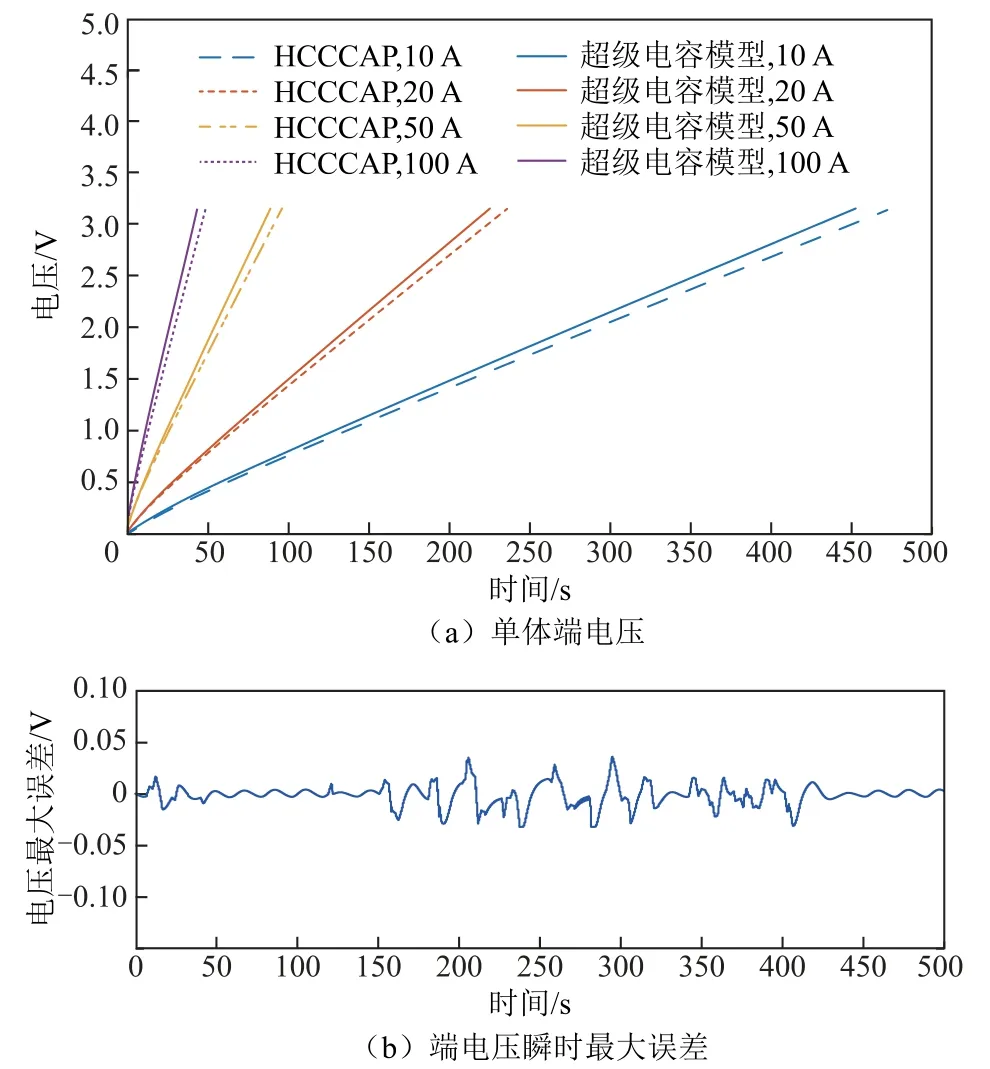
图6 不同充电电流下所提模型与HCCCAP 型超级电容单体端电压的对比Fig.6 Comparison of proposed model with HCCCAP type supercapacitor single terminal voltage at different charging currents

2 PMP 与工况构建结合的能量管理策略

2.1 传统PMP 能量管理策略

庞特里亚金极小值原理以变分法为基础[14]，对控制变量与目标函数求取极值，以获得全局最优解。为使有轨电车在循环工况行驶过程中燃料消耗最低，构建混合动力系统最小运行氢耗量目标函数J为

式中，Cfc和Csc分别为混合动力系统中燃料电池和超级电容的氢气消耗速率。

式中，a、b、c为通过对燃料电池功率Pfc与氢气消耗速率之间函数关系进行拟合得到的多项式系数；Psc为超级电容功率；γ为平衡超级电容SOC 的加权因子[18]，Pr为负载需求功率；H2LHV 为氢气低热值。

因此PMP 能量管理算法以燃料电池功率为控制变量，超级电容SOC 为状态变量。

为减小器件损耗，同时避免超级电容SOC 过充过放，约束条件为

由图5 的超级电容模型和安时积分法[19]，超级电容SOC 计算式为

其中

则可构建状态方程为

式中，λ为协态变量。

协态方程为

以哈密尔顿函数最小化为目标求解整个循环工况内的燃料电池最优功率，如式（18）所示。

λ的取值对PMP 能量分配性能有直接影响。在离线状态下，λ˙=0 ，即协态变量取常数[20]，计算流程如图7 所示，其中ζ为无穷小常数。

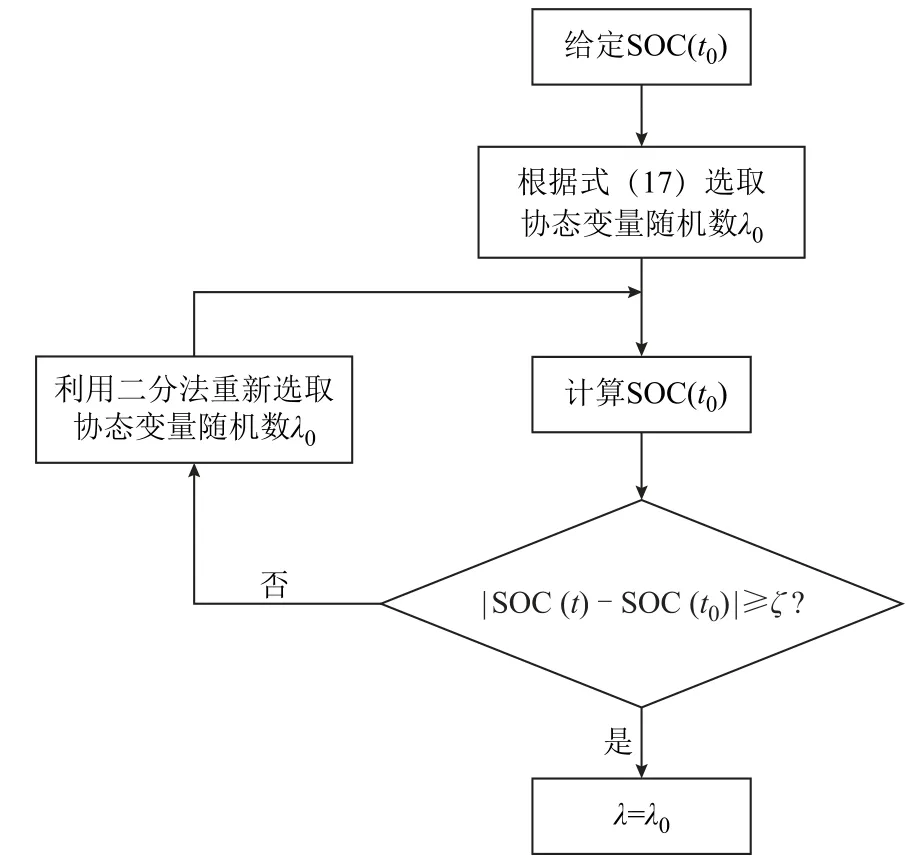
图7 协态变量计算流程Fig.7 Flow chart of covariate calculation

2.2 基于运行状态识别的有轨电车工况构建

本文研究的混合动力有轨电车路权形式为全封闭与半封闭路权交互[21]。在全封闭路权段，有轨电车独立运行；在半封闭路权段，为保持运行速度，使用主动信号优先原则中的绿灯延长控制原则，即交叉口处安装检测器以提示司机停车或直接通行，防止运行状态突变。依据电车速度、加速度和需求功率的不同风格对行驶过程中实时运动状态OST(t)进行识别，如式（19）所示。进而确定各动力源的工作条件，为选择供能模式奠定基础。

依据OST(t)的识别特征将电车行程按时间顺序依次分为怠速牵引、加速启动、稳速行驶、减速制动和再生制动五个阶段，如图8 所示。

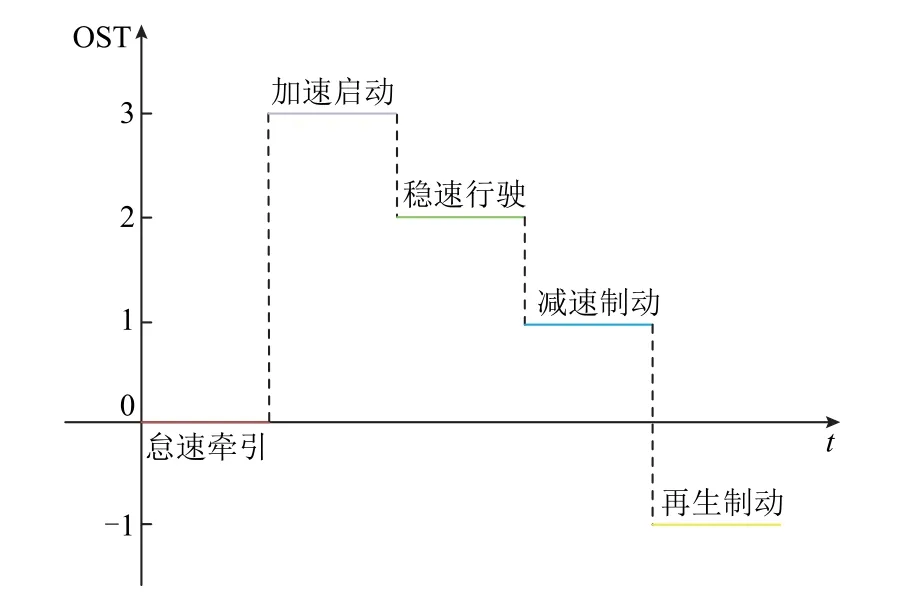
图8 有轨电车运行状态划分Fig.8 Tram operation state division

各阶段的运行特征为：

1）怠速牵引阶段：混合动力系统克服滚动阻力、风阻力、坡度阻力和其他阻力驱动电车预启动，燃料电池为超级电容充电。

2）加速启动阶段：速度从零加速到最高速的过程，依据表1 所示的整车技术指标，设定0～30 km/h过程中加速度为1 m/s2，30～60 km/h 过程中加速度为0.6 m/s2；这一阶段中输出功率持续增大，直到速度达到60 km/h 后牵引电机保持最大功率输出。

最后，知识产权评议是防范和化解重大投资项目知识产权风险的主要方法，是维护产业安全和优化产业布局的关键环节。在我国，政府投资的重大项目往往承载着促进区域经济发展、优化产业结构、满足公共需求等政策功能。通过对区域内重大投资项目、招商引资项目和产业发展规划等进行知识产权评议，可以及时发现其中的知识产权风险并提前做好防范和化解工作（包括开展储备性、应对性的知识产权管理和运营），从而起到维护产业安全、优化产业布局的作用。

3）稳速行驶阶段：此阶段速度不为零且加速度绝对值不大于0.1 m/s2。

4）减速制动阶段：有轨电车在进站前预先减速，超级电容和制动电阻开始吸收制动能量。

5）再生制动阶段：在电车减速过程或进站停靠后将制动能量反馈到直流母线。

依据图8 划分的连续性运行状态虽能描述电车行驶工况所承载的主要动力学特征，但由于线路的地理特征、交通流状况及驾驶员的驾驶风格等方面的差异，致使同一状态下不同时刻间仍存在高度随机性，因此需借助马尔科夫链描述电车运行瞬时随机性。将传感器采集到的车速和需求功率分别划分成m和n个区间，构成离散网格空间。当k时刻车速为vk时，有轨电车需求功率由当前时刻状态Pir转变为下一时刻状态Pjr的转移概率pij，有

依据转移概率元素Mij构成矩阵的过程为

式中，Nij为需求功率由 riP转移到 rjP的次数。

由于马尔科夫链有随机性和无后效性，因此依据以上模型，可以在有轨电车行驶过程中由当前时

刻数据借助一步转移概率矩阵M得到多步转移概率分布。考虑到随着预测步长的增加，得到的预测值与实际值的偏差逐渐增大[22]，所以电车需求功率预测值分布为

统计北京现代有轨电车西郊线的运行速度、加速度、需求功率等信息，依据式（19）判据对行驶过程进行运行状态划分，并构建转移概率矩阵，结果如图9a～图9e 所示；不区分运行状态，采用传统马尔科夫链构建的需求功率状态转移概率矩阵如图9f 所示。从图9 中可以看出，电车在各运行阶段状态转移概率分布是不同的，相较于研究完整行驶循环的方式，采用所提方法能够更加真实地体现有轨电车在行驶过程中的随机性与波动性。

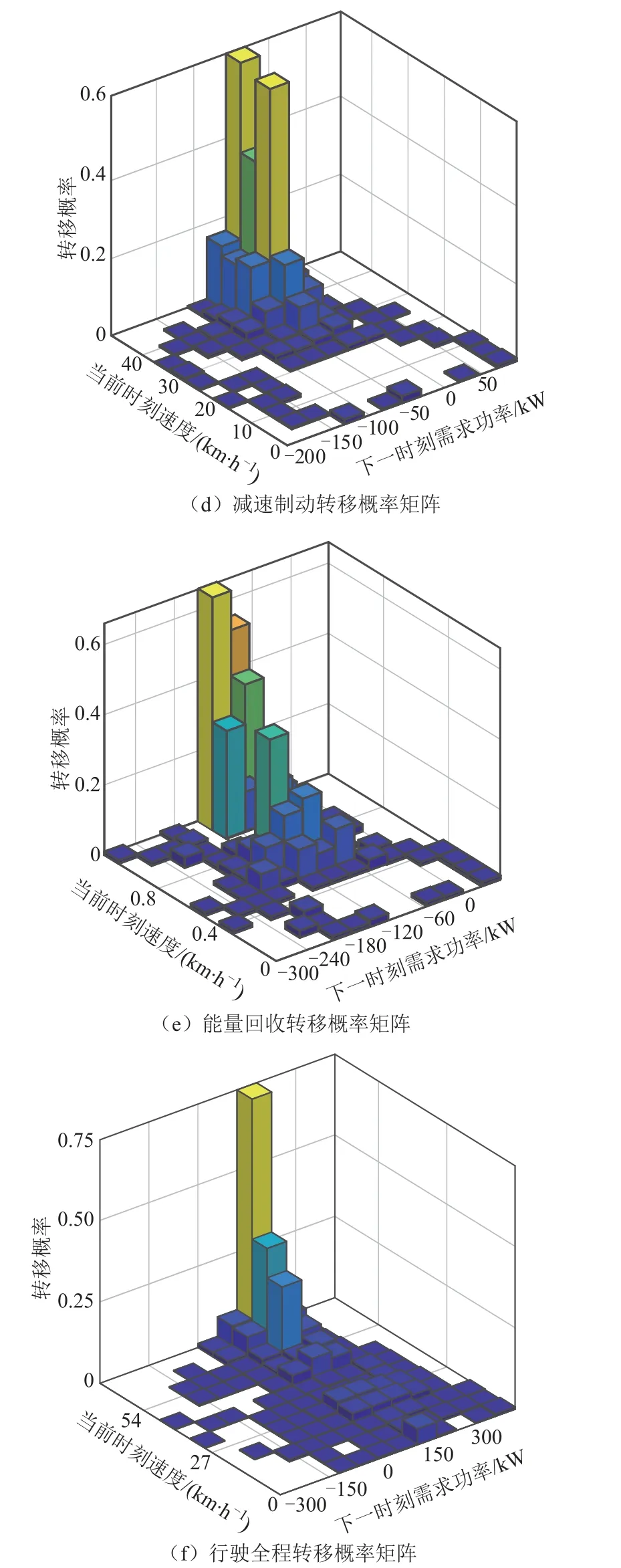
图9 不同运行状态转移概率矩阵Fig.9 Transition probability matrix of different operating states

2.3 功率预测精度验证

马尔科夫预测方法的误差会随着预测时间的延长而增加[23]。针对文中研究的混合动力系统，考虑工况适应性与控制鲁棒性，设置功率预测模块的采样时间为1 s，预测时长为3 s。采集并记录武汉东湖线和北京西郊线有轨电车0～2 000 s 内行驶速度、实际需求功率等数据构建样本数据库，同时应用上述方法预测两工况下的需求功率。将仿真得到的需求功率曲线与采集到的实际运行功率曲线进行对比，验证结果如图10 所示。

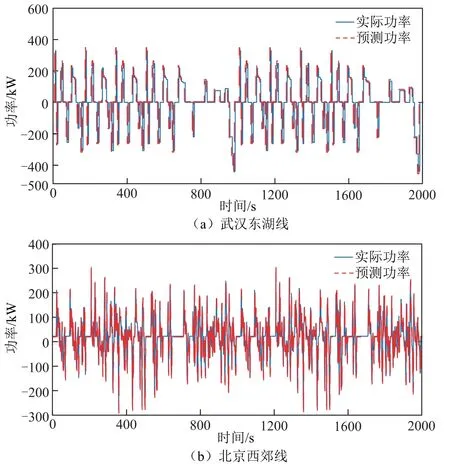
图10 需求功率预测对比验证Fig.10 Demand power forecast comparison verification

从图10 中可以看出，有轨电车需求功率的仿真曲线在两种工况下均能较准确地贴近实际功率曲线。

同时，为了进一步验证预测工况的准确性，进行需求功率分布误差对比，统计两种工况下的预测需求功率的点相较于样本数据库总体平均值的瞬态误差，对比结果如图11 所示。

图11 两种工况下需求功率分布误差的对比Fig.11 Comparison of demandpower distribution error under twooperating conditions

从图11 中可以看出，两种工况下瞬态误差均在±1%以内，说明运行状态识别工况构建方法能够真实地重现有轨电车运行场景及其特性。

2.4 融合功率预测的PMP 能量管理策略

传统PMP 作为一种基于全局优化的经典策略，在已知工况条件下能够实现全局最优功率分配与最少氢气消耗量。但将其应用到轨道交通电车时，高功率负载突变致使能量管理系统无法及时跟踪电车运行状态进行调整，存在实时性与工况适应性差的缺陷。与此同时燃料电池作为主动力源，启动和停止过于频繁会直接影响其使用寿命。因此考虑引入基于电车运行状态识别的需求功率预测，兼顾能量管理策略的工况适应性与燃料电池的工程适用性（即在减少燃料电池启停次数的同时尽可能提升其工作效率）。

首先依据式（23）计算燃料电池堆发电效率ηfc，得到理想的功率-效率曲线；然后利用式（24）和式（25）分别确定效率期望E(ηfc)以及对应的离散度标准差σfce；进而基于发电效率所处的取值区间，将燃料电池工作状态划分为低效、中效、高效和超高效四种模式，如图12 所示。

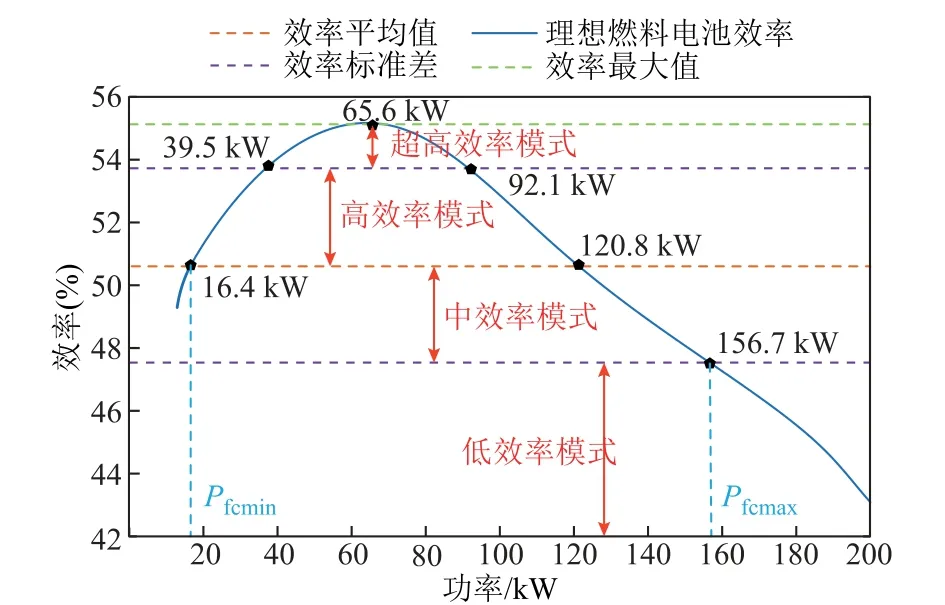
图12 燃料电池堆基于发电效率划分的工作模式Fig.12 Working modes of fuel cell stack based on on the power generation efficiency division

式中，Pfc为燃料电池堆输出功率；PH(ηfc)为燃料电池堆发电效率的概率密度函数；积分下限值对应以额定效率（50%）启动的输出功率。

为提升燃料电池供能效率，设定启动规则为：以超高效率、高效率或中效率模式启动，低效率模式时不启动。根据图12 曲线各交点，确定启动区间[Pfcmin,Pfcmax]。则启动判据为：若式（18）求取的最优输出功率，燃料电池启动于当前工作模式，同时依据2.2 节所述需求功率预测方法确定k时刻与k+1 时刻之间的转移概率，再共同代入式（26）计算k+1时刻的最优输出功率；若燃料电池停止启动，为零，下一时刻由超级电容承担全部需求功率并更新SOC 值。

综上所述，整体能量管理策略如图13 所示。

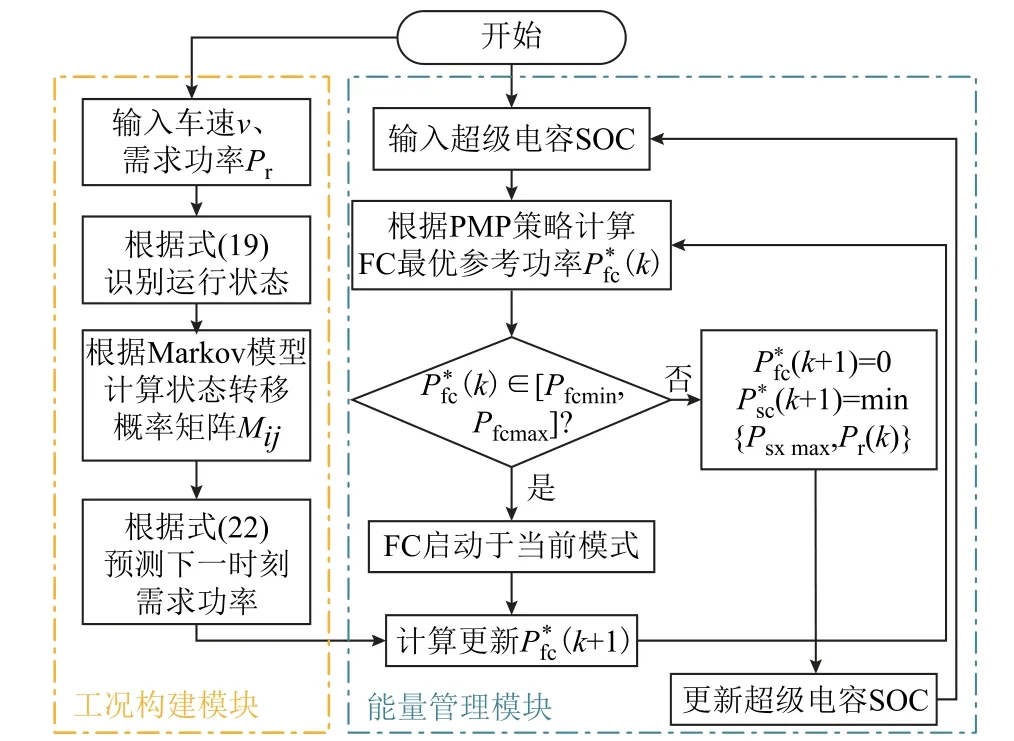
图13 融合功率预测的PMP 能量管理策略Fig.13 PMP energy management strategy based on power prediction

3 仿真验证

基于图1 所示的混合动力系统主动式拓扑结构、图2 所示的燃料电池电堆动态参数模型及图5 所示的超级电容阻抗衰减等效模型，在Simpowersystem环境下搭建能量管理策略在线验证仿真平台。燃料电池电堆仿真定义参数见表2，超级电容组的单个模块仿真定义参数见表3。

表2 燃料电池电堆仿真定义参数Tab.2 Simulation definition coefficients of fuel cell

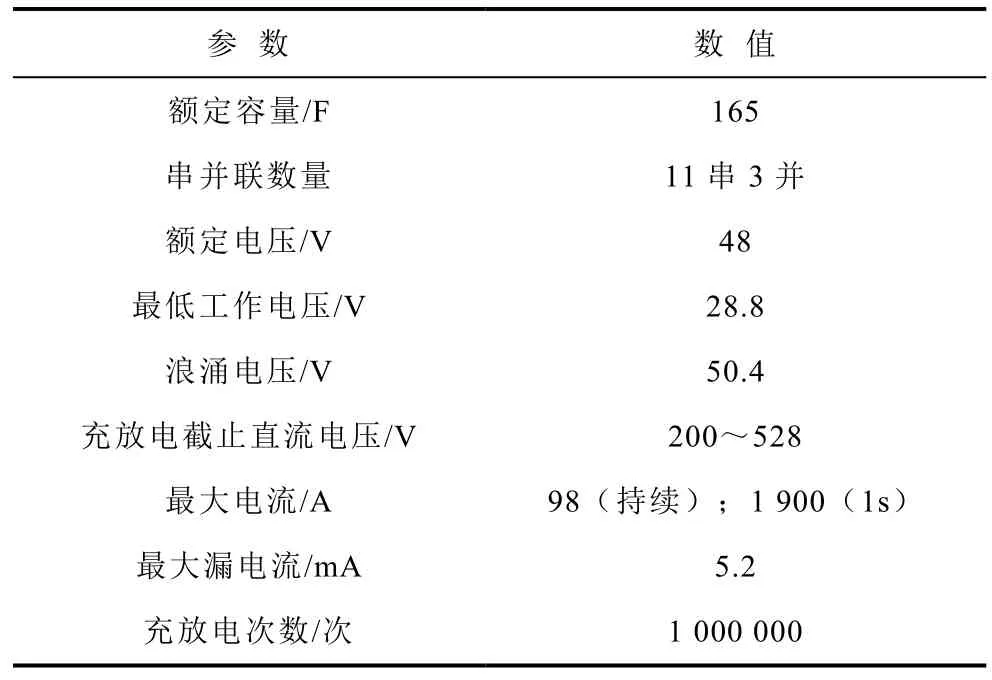
表3 超级电容组单个模块主要技术参数Tab.3 Technical parameters of vehicle supercapacitor module

经典全局PMP 能量管理策略应用于工程实际中时，协态变量对计算精度影响较大，需提前已知完整工况，因此对负载突变的鲁棒性表现不佳。

典型瞬时ECMS 是PMP 策略的延伸[24]。引入等效因子将系统消耗电能等效为耗油量，通过实时最小化等效燃油消耗以实现经济性目标。目标函数为

式中，ΔT为采样时间；s为等效因子，表达式为

式中，µ为超级电容SOC 平衡系数，根据经验取0.65[25]，以维持充放电过程荷电状态平衡。

但由于在不同运行情况下ECMS 的等效因子均固定，所以工况适应性较差。

为验证本文所提策略兼具实时性与全局性，在相同容量配置参数下，将本文所提策略与传统PMP、ECMS 能量管理策略分别在两种测试工况中进行对比验证。为与选用的工况条件相匹配，设置双层电容组荷电状态初始值为85%；功率预测模块的采样时间为1 s，预测时长为3 s；仿真运行时间典型工况下为2 000 s，非典型工况下为1 500 s。

3.1 典型行驶工况系统性能对比分析

选取实测的典型有轨电车行驶工况作为能量管理策略的输入条件，此工况呈现的特征为由恒定加速度、减速度的短行程片段拼接而成的“模态循环”，且不考虑道路坡度因素，即道路坡度为零。有轨电车速度、加速度与需求功率历程如图14 所示。

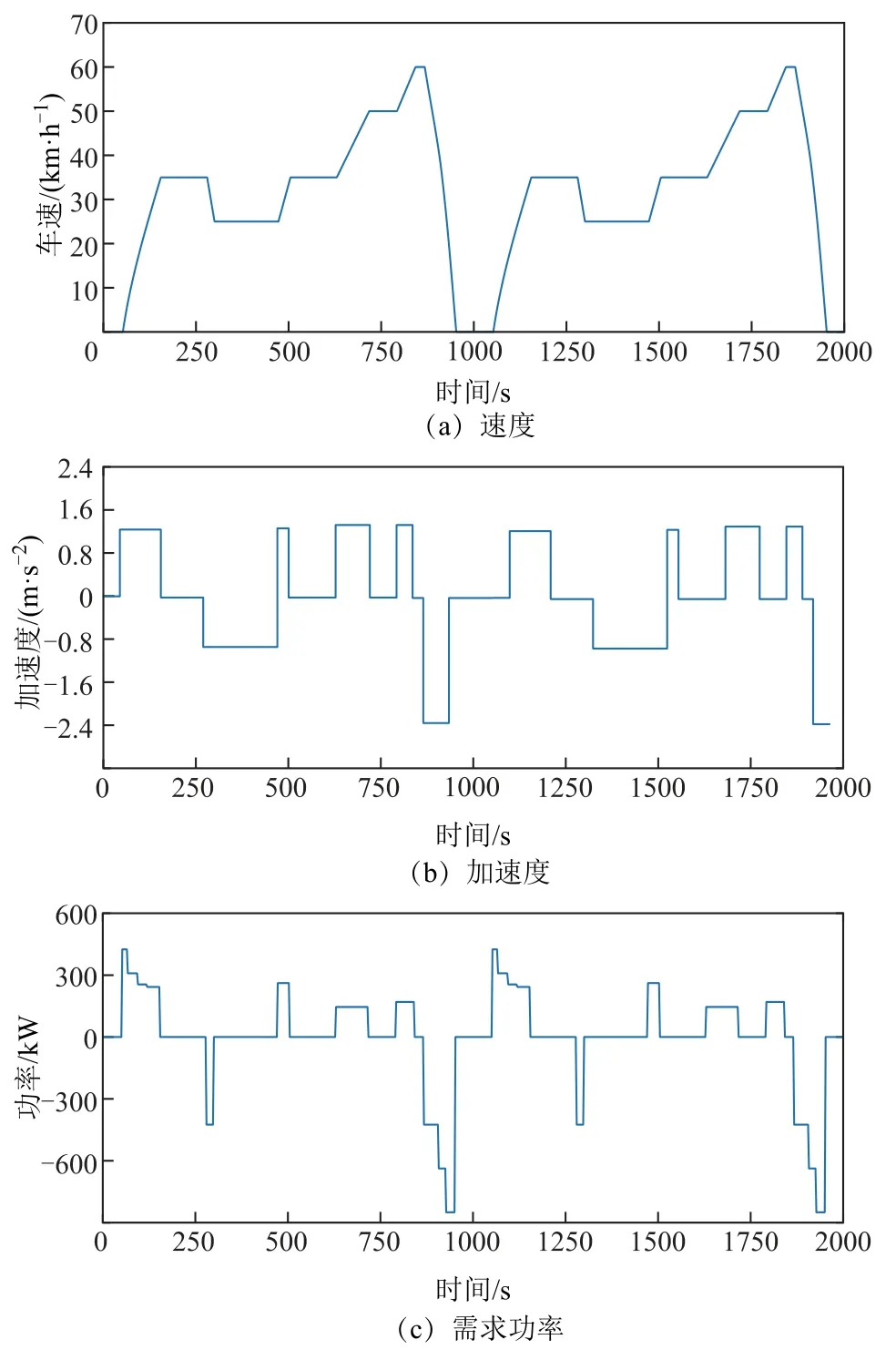
图14 典型工况行驶历程Fig.14 Typical working condition operating histories

3.1.1 混合动力系统瞬时功率分配与能量管理策略优化算法耗时

典型行驶工况下功率分配对比如图15 所示，结果表明三种策略均能满足需求功率需求，维持电车续航能力。图15 对比表明，相较于ECMS 和传统PMP 策略，本文所提策略通过引入运行状态划分，精确预判高需求功率时刻，增加了超级电容峰值出力的频率和幅值，进而减轻了燃料电池负载压力，实现了最为平滑的主动力源输出功率曲线。

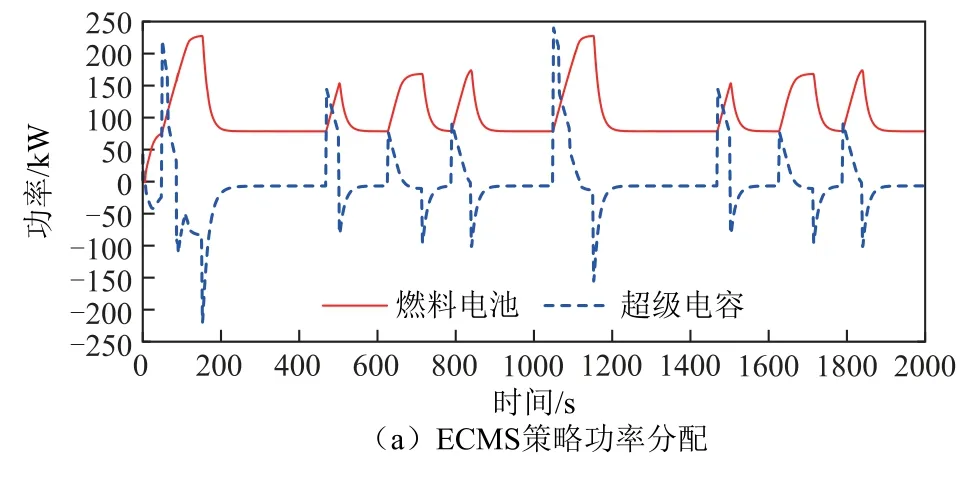
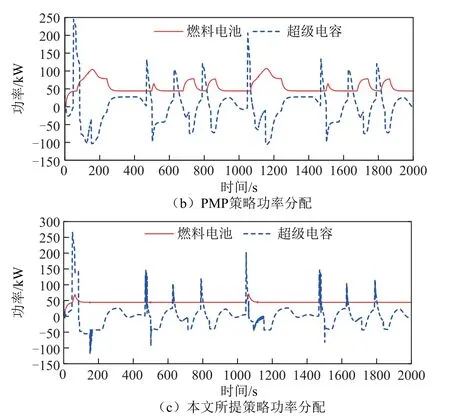
图15 典型工况下的功率分配对比Fig.15 Comparison of power distribution under typical operating conditions

另外，从图15 中可以直观地看出，在整个行驶工况中，三种策略下燃料电池高功率启动次数及峰值功率波动时间对比见表4。

表4 典型工况下燃料电池高功率性能比较Tab.4 Comparison of fuel cell high power performance under typical operating conditions

在 Matlab2018b 仿真环境下利用配置为 Intel Core i5-7200U @2.50GHz 的计算机得到典型工况下三种能量管理策略优化算法计算时间见表5。从表5 中可以看出，与传统PMP 策略相比，本文所提策略由于无需已知全部工况，计算量大大降低，耗时明显缩短；与ECMS 策略相比，计算时间略长。但综合表4 数据，本文所提策略能够大幅度减少燃料电池的高功率启动次数和峰值功率波动时间，从而使得需求功率突变时混合动力系统能够更快速地提供能量。在延长燃料电池使用寿命的基础上进一步增强系统速动性。

表5 典型工况下优化算法计算时间Tab.5 Time-consuming of different optimization algorithms under typical operating conditions

3.1.2 混合动力系统全局氢耗量与平均效率

三种策略下系统氢燃料消耗量比较结果如图16 所示。本文所提策略消耗氢气量为3.76 kg，与PMP策略消耗4.13 kg 和ECMS 策略消耗4.52 kg 相比，分别降低了9.6%和16.8%。由此表明本文所提策略在典型行驶工况中表现出全局最优的燃料经济性。

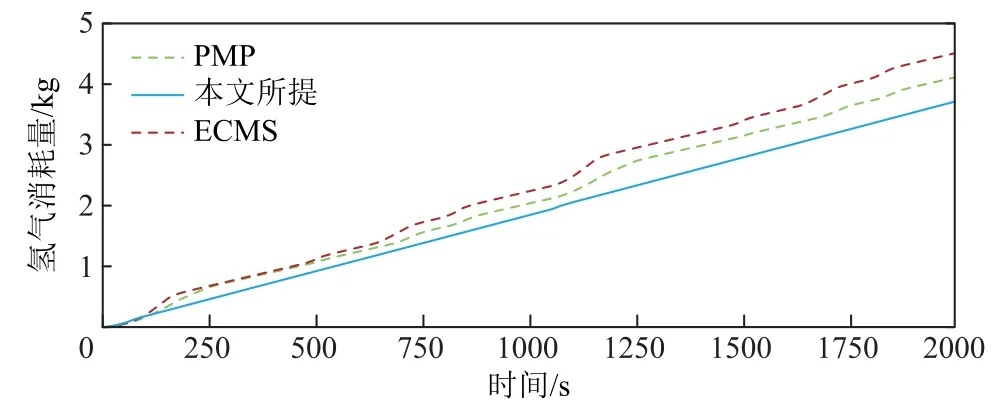
图16 典型工况下的系统氢耗量对比Fig.16 Comparison of system hydrogen consumption Comparison of power distribution under typical operating conditions

依据能量利用率原理[24]，混合动力系统运行整体效率E为

对整个工况中瞬时整体效率计算结果进行统计，本文所提策略总体平均值为86.2%，高于PMP和ECMS 策略下的76.5%和69.2%。有所精进的原因为随着燃料电池输出能量的提升，在制动电阻上的热损耗也会随之增大，进而导致能量利用率降低。

3.1.3 超级电容荷电状态、电流与直流侧母线电压

典型工况下超级电容SOC 波动情况对比结果如图17 所示。由图17 中可以看出，在三种策略的控制下，SOC 偏差都控制在允许范围内。本文所提策略、PMP 策略、ECMS 策略与初始值相比，SOC 瞬时最大偏差分别为5.5%、9.7%、7.8%，末态值分别为84.9%、92.5%、82.3%。由此表明，ECMS策略中由于等效能量因子依赖专家经验，对需求功率评估准确度较低，进而导致超级电容输出过多能量以支持主电源，末态荷电状态值较低；传统PMP策略由于不具备瞬时优化特性，只从工况全局出发，较为粗糙地判定超级电容充放电情况，进而导致瞬时和末态荷电状态偏移初态的范围最大；而对于本文所提策略，由于融入了马尔科夫链在线预测需求功率，能够依据燃料电池工作效率模式灵活调整启停状态，在维持超级电容荷电状态全局性始末平衡的基础上，实现瞬时最窄的偏移初始值范围。

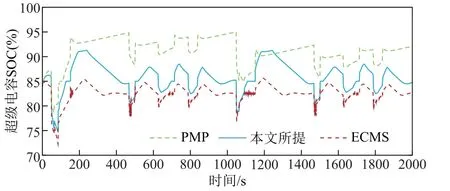
图17 典型工况下的超级电容SOC 对比Fig.17 Comparison of supercapacitor SOC under typical operating conditions

典型工况下，超级电容的电流极值分别为Iscmax=400 A，Iscmin=-400 A。一旦电流超过此范围，在DC-DC 变换器的作用下会使母线电压随之发生波动。超级电容电流与直流侧母线电压在三种策略下的对比如图18 所示。从图18a 中可以看出，ECMS策略、传统PMP 策略和本文所提策略下超级电容峰值电流分别为-385.7、400 和-199.8 A，说明本文所提策略能够保持超级电容更加稳定地向系统提供能量。从图18b 可以看出，ECMS 策略的母线电压偏移范围为±5.9%；传统PMP 策略为±4.2%；本文所提策略为±3.3%，并且在运行结束时本文所提策略的母线电压值最接近初值。这是因为在功率预测与燃料电池工作模式划分模块的共同作用，使得各动力源能够平稳出力，进而提升混合动力系统应对需求功率突变的鲁棒性。

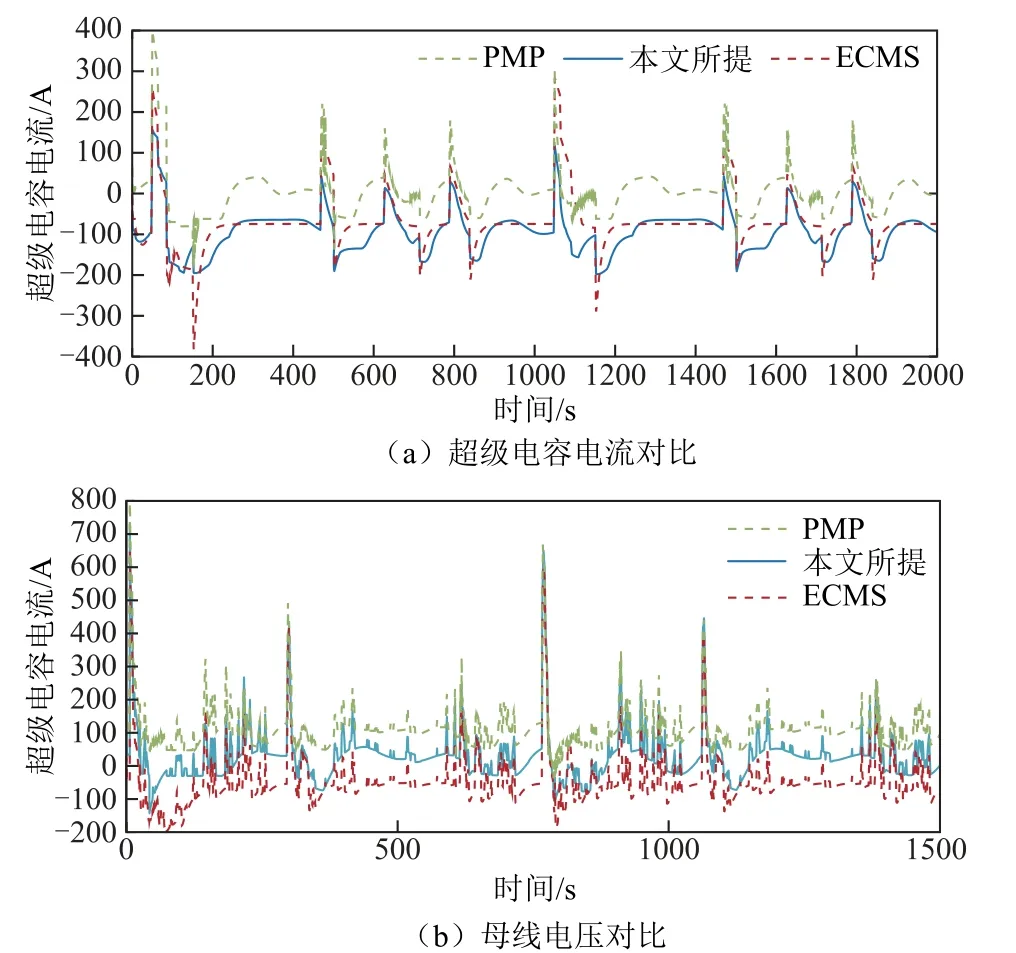
图18 典型工况下直流侧母线电压和超级电容电流对比Fig.18 Comparison of DC side bus voltage and super capacitor current under typical operating conditions

3.2 非典型行驶工况系统性能对比分析

选取实测的非典型有轨电车行驶工况作为能量管理策略的输入条件，此工况呈现的特征为考虑加速度时变性的动态性能并结合时空相关性的道路坡度状态的“动态循环”，需求功率曲线出现瞬时尖峰特征，瞬时波动性强，较真实地反映了驾驶场景。有轨电车非典型工况行驶历程如图19 所示。

图19 非典型工况行驶历程Fig.19 Atypical working condition operating histories

3.2.1 混合动力系统瞬时功率分配与能量管理策略优化算法耗时

非典型行驶工况下功率分配对比结果如图20所示，三种策略下超级电容组输出功率波动范围均远高于燃料电池电堆，有效地减轻了主电源高峰值需求功率压力。本文所提策略相较于ECMS 策略，燃料电池功率曲线可近似为平直线，因此需求功率所带来的大范围剧烈扰动可忽略不计；相较于PMP策略，本文所提策略燃料电池功率瞬时波动更加平缓。综上所述，本文所提策略应对有轨电车负载突变的鲁棒性和适应性最强。

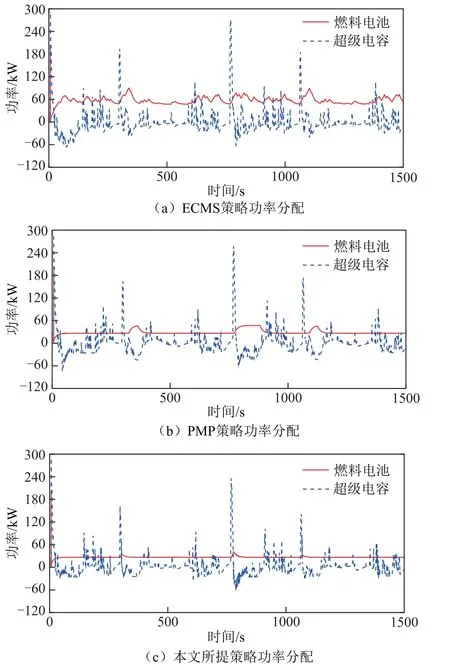
图20 非典型工况下的功率分配对比Fig.20 Comparison of power distribution under atypical operating conditions

与典型工况类似，由图20 中可得到非典型仿真工况中燃料电池高功率启动次数及峰值功率波动时间的对比，见表6。

表6 非典型工况下燃料电池高功率性能比较Tab.6 Comparison of fuel cell high power performance under atypical operating conditions

在与3.1.1 节仿真环境与计算机配置相同的前提下，非典型工况的三种能量管理策略优化算法计算时间见表7。与典型工况类似，本文所提策略相较于传统PMP 策略，算法耗时下降明显。综合表6数据，本文所提策略与其他两种传统策略相比，能够大幅度减少燃料电池的高功率启动次数和峰值功率波动时间，从而使得需求功率突变时混合动力系统能够更快速地提供能量。在延长燃料电池使用寿命的基础上进一步增强系统速动性。

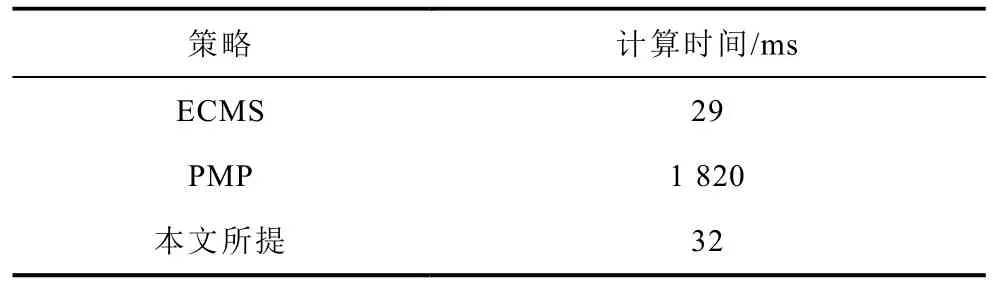
表7 非典型工况下优化算法耗时Tab.7 Time-consuming of different optimization algorithms under atypical operating conditions

3.2.2 能量管理策略全局氢耗量与平均效率

三种策略在非典型工况行驶过程中系统氢气消耗量对比如图21 所示，在工况结束时刻，本文所提策略消耗量为5.25 kg，相较于PMP 和ECMS 策略消耗的5.52 kg 和5.92 kg，分别降低了4.9%和11.3%；本文所提策略系统效率总体平均值为82.5%，相较于PMP 和ECMS 策略下的77.3%和70.8%有所提升。上述指标对比结果证明了本文所提策略对提升用氢效率和改善能量利用率具有广泛的代表性和普适性。

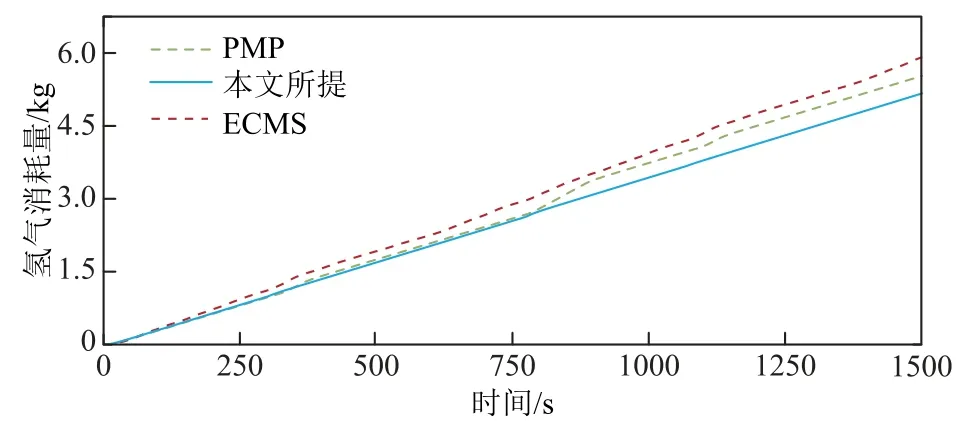
图21 非典型工况下的系统氢耗量对比Fig.21 Comparison of system hydrogen consumption under atypical operating conditions

3.2.3 超级电容荷电状态、电流与直流侧母线电压

非典型行驶工况下超级电容SOC 对比结果如图22 所示。虽然在三种策略下超级电容SOC 均能跟随需求功率峰值趋势波动，但本文所提策略SOC最大偏移率为24.9%，与传统PMP 和ECMS 策略下27.8%和28.6%的偏移率相比有所降低，同时能够使SOC 始末值最趋近于保持一致。上述结果表明，在负载冲击性强的工况中，本文所提策略对降低超级电容能量源应力、维持稳定运行有最大的贡献，进而能够更加合理地利用超级电容的能量，以减少系统氢耗量，并延长储能系统充放电使用寿命。

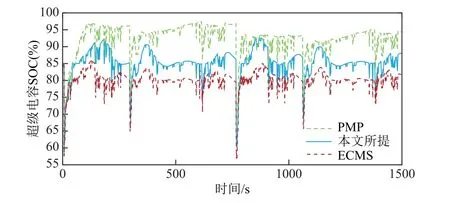
图22 非典型工况下的超级电容SOC 对比Fig.22 Comparison of supercapacitor SOC under typical operating conditions

非典型工况下，超级电容的电流极值分别为Iscmax=800 A，Iscmin=-200 A。超级电容电流与直流侧母线电压在三种策略下的对比如图23 所示。从图23a 中可以看出，超级电容峰值电流在ECMS 策略、传统PMP 策略和本文所提策略下分别为-200、800、-147.7 A，即本文所提策略能够降低电流过高对超级电容造成的冲击，进而延长使用寿命。从图23b可以看出，母线电压偏移范围在ECMS 策略、传统PMP 策略和本文所提策略下分别为±6.7%、±5.3%和±3.7%，即本文所提策略能够显著抑制直流侧母线电压的波动，使混合动力系统更加稳定运行。

图23 非典型工况下母线电压和超级电容电流对比Fig.23 Comparison of bus voltage and supercapacitor current under atypical operating conditions

典型工况与非典型工况下的混合动力系统运行效能指标仿真结果对比见表8。由此表明，相较于经典全局和瞬时优化能量管理策略，本文所提策略应对稳态循环与动态循环负载，在节能、高效、稳定运行方面能够实现多重最优。

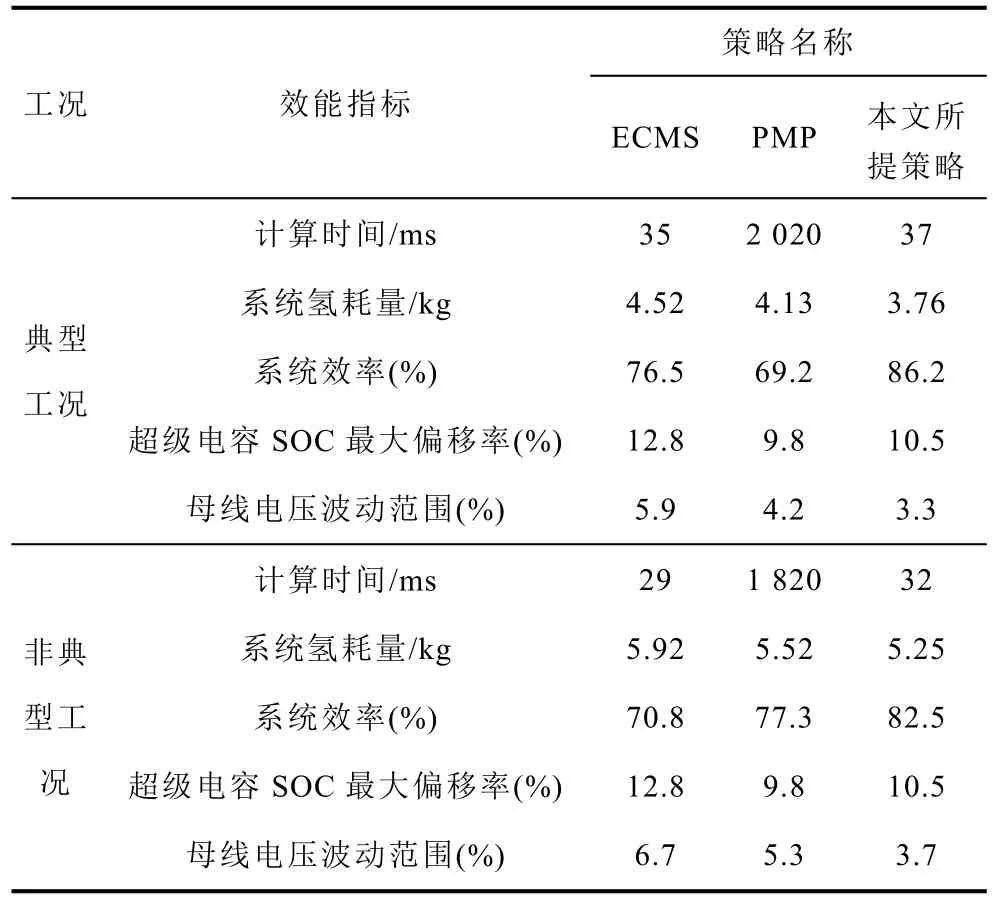
表8 仿真结果对比Tab.8 Comparison of simulation results

4 结论

采用极小值原理与马尔科夫链功率预测相结合的方法对有轨电车用多动力源系统进行能量管理的核心优势在于：

1）克服了以传统极小值原理为代表的全局优化策略实时性与工况适应性差的缺陷，使混动系统功率分配兼具瞬时与全局最优特性。

2）引入基于电车运行状态识别的需求功率预测并划分燃料电池工作模式，提升了能量管理策略的工况适应性，同时避免了燃料电池的频繁启停。

3）本文所提策略相较于传统极小值原理和ECMS 策略，氢气消耗量在典型工况下分别降低了9.6%和16.8%；在非典型工况下分别降低了4.9%和11.3%，系统整体能量利用效率分别提升至86.2%和82.5%，同时超级电容SOC 波动范围在两种工况下均有显著改善。

本文所提策略控制结构简单、易于实现，并在典型和非典型的有轨电车行驶工况中在线验证了其有效性和优越性，工程应用前景广阔。