计及温度不确定性的配电网广义储能分层调控策略

刘志伟 苗世洪 杨炜晨 姚福星 王廷涛

（强电磁工程与新技术国家重点实验室（华中科技大学电气与电子工程学院） 武汉 430074）

0 引言

在国家双碳战略目标推动下，越来越多的风电、光伏等可再生能源发电将接入配电网中，在清洁、环保的同时，也配电网的安全稳定运行带来了严峻挑战[1]。目前，在配电网中通常配置诸如蓄电池、超级电容器等常规储能设备，用以维持电网的功率平衡，提高可再生能源的消纳率。然而，常规储能设备的建造、维护成本高昂[2-3]，不利于配电网的经济性。

近年来，负荷需求响应技术受到较多的关注和发展，其能够服务于电网的优化运行，维持功率平衡，提高可再生能源的利用率[4]。其中，具有储能特性的空调负荷作为需求响应的重要资源，在用户负荷中占比较高[5]，具有调控潜力大、响应迅速等性能[6]。通过直接负荷控制，空调负荷可转换为成本低廉、调控特性良好的广义储能[7]，主动参与到配电网的调控管理中，能够有效减少传统储能设备的投资，提高电网设备利用率，对于促进可再生能源的消纳、提高配电网的经济运行水平具有重要意义。

为发挥空调负荷广义储能在配电网中的调控潜力，文献[8]基于定频空调的运行特性，建立了虚拟储能模型及其特性评估指标，并将其应用于电网临时性削峰；文献[9]将变频空调等效为热储能电池，并与传统锂电池进行对比分析，证明了变频空调的良好调控特性，可为电网调度提供服务；文献[10]根据变频空调不同控制策略，分别建立了容量型储能与功率型储能模型，并研究了这两类模型的应用场景；文献[11]将变频空调应用于电网的一次调频，定频空调应用于二次调频，实现定频空调与变频空调的协调控制，提高了调频效果。综上所述，将空调负荷等效为虚拟储能，可应用于负荷削峰、优化调度、功率波动平抑及调频服务，提高了电网运行的安全经济性。然而上述文献未考虑调控过程中外界不确定性因素的影响，当外界因素预测误差较大时，常规确定性调控策略难以保证电网运行的可靠性。

为处理不确定性变量，提高配电网运行可靠性，目前通常采用随机优化、鲁棒优化及分布鲁棒优化的方法。随机优化需要随机变量确切的概率分布[12]，鲁棒优化存在优化结果过于保守的问题[13]，而分布鲁棒优化则结合了随机优化与鲁棒优化的优点，在经济性和保守性方面均具有较好的特性[14]。文献[15-16]建立了变频空调的虚拟储能模型，并将其应用于电网的调度，同时采用鲁棒优化方法处理可再生能源出力的不确定性。文献[17]建立了含热负荷的广义储能模型，并针对可再生能源出力及负荷响应的不确定性，采用可调鲁棒方法。文献[18]建立了相变储能与建筑物的动态储能模型，并提出两阶段分布鲁棒优化调度策略，以应对风电出力的不确定性。上述文献考虑了温控负荷在参与电网调度过程中不确定性因素的影响，但主要集中在风电、光伏出力等不确定性因素对电力系统的影响，并未涉及环境温度等因素对建筑物房间热力过程的影响，难以保证用户使用舒适度。同时对于空调负荷均以集群的方式进行调控，未充分考虑集群内各空调负荷的状态差异及功率分配问题。

对上述问题，本文将变频空调视为广义储能，提出计及温度不确定的配电网广义储能分层调控策略。首先，建立变频空调广义储能模型，并以广义储能特征参数为基础，提出了广义储能聚合方法；然后，构建广义储能集群分层调控框架，在广义储能集群调控层面，提出配电网广义储能集群分布鲁棒优化调控策略，避免了室外温度不确定性影响用户舒适度，并将机会约束松弛转换为确定性线性约束，实现模型有效求解，在广义储能群内调控层面，提出广义储能集群群内功率分配策略，实现广义储能等效荷电状态变化的一致性，保障了调控的公平性；最后，基于改进的IEEE 33 节点算例验证了所提策略的有效性。

1 空调负荷的广义储能模型

1.1 变频空调数学模型

变频空调具有调节迅速、温控精度高、节能等优点，已逐渐代替传统定频空调，在空调市场的占比逐渐升高[19]。与定频空调仅具有开启与停止两种状态不同，变频空调通过动态调节压缩机的频率来控制其制冷（热）量，实现室内温度的快速调节。目前市场上的变频空调均能在数十秒内调节压缩机运行至高频状态。本文以制冷变频空调作为研究对象，建立其热力学模型与热电转换模型。

1.1.1 热力学模型

目前通常使用等效热参数（Equivalent Thermal Parameters, ETP）模型来描述空调房间温度的动态变化规律。为简化计算，本文忽略日照强度、人类行为活动的影响，建立空调房间的一阶ETP 模型为[8]

式中，Qac为空调的制冷量；Tin与Tout分别为室内与室外温度；Ra为空调房间的等效热阻；Ca为空调房间的等效热容。

1.1.2 热电转换模型

与定频空调具有恒定的能效比不同，变频空调的热电转换效率与压缩机的频率有关，压缩机频率越高，空调的热电转换效率越低。根据文献[20]的实验结果，可近似将变频空调的电功率与制冷量表达为压缩机频率的一次函数，即

式中，Pac为空调的电功率；fac为空调压缩机的频率；k1、k2、b1、b2为一次函数系数。

进而得到空调制冷量与电功率的关系为

1.2 变频空调广义储能模型

空调-建筑物系统具有一定的储热能力，能够将空调电能转换为热能储存于建筑物中。因此，可将空调-建筑物系统等效成广义储能设备，在保证用户舒适度的条件下，通过直接负荷控制的方式参与到电网调控体系中，有利于提高电网运行的安全经济性。对于用户而言，在调控过程中空调房间温度将在设定范围内波动，根据人体热感觉投票值（Thermal Sensation Vote, TSV）模型[8]，用户能够接受室温在一定范围内变化，同时会获得对应的补偿。因此，在用户角度上，调控变频空调能够在满足舒适度的前提下获得一定收益；而在配电网角度上，调控变频空调能够降低其整体运行成本。

空调房间内温度的变化反映了系统存储热量的变化，根据空调房间ETP 模型，当室内温度从T1上升（下降）至T2时，系统所放出（吸收）的热量ΔEac为

为满足用户舒适度需求，设置室温变化范围为[Tin,min,Tin,max]，则当室内温度从Tin上升至Tin,max时，系统所放出的热量达到最大值，定义此时系统的储能量为0。由此可得，当室内温度为Tin时广义储能的储能量Eac为

相应地，当室内温度为Tin,min时，系统的储能量最大，定义广义储能的容量EacN为

进而，为实时表征广义储能的储能状态，仿照储能电池，定义广义储能的等效荷电状态ESOC为

当调控步长Δt较小时，空调房间热力学方程式（1）可近似用差分方程表示为

将式（4）与式（8）代入式（9）进一步得到

式中，α、β、γ、λ为广义储能模型的特征参数。

式（10）表示广义储能等效荷电状态随电功率及室外温度的变化情况。为满足用户舒适度需求，广义储能等效荷电状态满足约束

此外，受空调压缩机频率的限制，广义储能的功率需满足

式中，Pac,min与Pac,max分别为广义储能最小与最大有功功率，由空调压缩机运行频率决定；Qacq为广义储能的无功功率；acφ为广义储能的功率因数角。

综上所述，单台变频空调的广义储能模型可由式（10）～式（13）表示，其数学形式和运行特性与储能电池类似，因此可通过调控广义储能的输出功率，以满足电网的经济运行需求。

1.3 广义储能集群模型

在配电网中，用户侧的空调数目众多，可以达到几百台甚至几千台，若直接对每台空调进行单独控制，将大大增加调控的复杂程度，系统的通信成本较高，控制可靠性较低，不具备实际实施的可行性。因此需要对大量分散的空调进行聚合，以集群的形式统一参与配电网的调控。

一般来说，由于空调的型号、建筑物的材料结构不同以及受室内人员的活动的影响，各广义储能的特征参数呈现明显的差异性，在聚合时难以将各个单独的广义储能模型直接相加。由式（10）可知，广义储能等效荷电状态的变化特性主要受特征参数α与β的影响。因此，可基于特征参数α与β对广义储能进行k-means 聚类，将广义储能划分为多个集群。对于聚类后的广义储能集群，其特征参数α、β为集群内所有广义储能对应参数的平均值，γ、λ为集群内所有广义储能对应参数之和。这一过程可由负荷聚合商来完成，聚合后的广义储能集群模型可表示为

令ESOCeq=ESOCΣnc，相应地，广义储能集群所需满足的约束为

若要维持广义储能集群的初始荷电状态ESOCΣ0不变（即各房间内初始设定温度Tset0不变），集群需以基准功率PacbΣ运行，即

式（14）～式（17）构成了广义储能集群模型，从而形成“配电网-负荷聚合商-用户”的分层调控架构，如图1 所示。负荷聚合商首先获取各广义储能的参数信息并对其进行聚类，随后向电网调控中心上报广义储能集群的特征参数，电网调控中心根据电网安全经济运行需求，对负荷聚合商下发功率调控指令。在此基础上，负荷聚合商基于集群内各广义储能的ESOC等状态信息，根据相应的功率分配策略，对各广义储能的终端控制器下发控制指令，通过调节空调压缩机的频率实现对功率指令的响应。

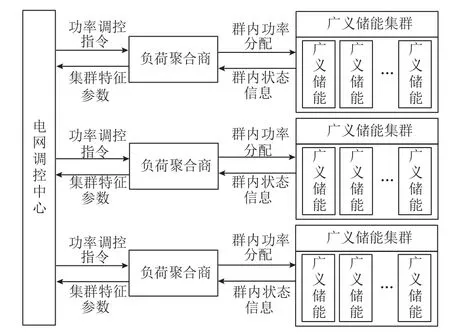
图1 广义储能集群分层调控架构Fig.1 Hierarchical regulation architecture of generalized energy storage cluster

在调控过程中，电网调控中心不需要与所有用户终端建立通信，仅需收集广义储能集群的相关信息并对集群下达调度指令，从而减小了数据计算量，减轻了通信负担，保护了用户的隐私。

在本文的调控架构中，配电网方与用户签订广义储能调控协议，包括：①用户侧广义储能功率受配电网方调控；②配电网方需保障用户舒适度不受影响；③配电网方需向用户支付调控报酬。在对广义储能进行调控时，配电网方需首要保障用户舒适度，在满足用户舒适度的前提下降低其运行成本。

此外，广义储能的调控复杂度和聚类精确度与聚类组数密切相关。聚类组数越多，集群内的广义储能参数相差越小，聚类精度越高，但是调控越复杂；反之，聚类组数越少，调控越简单，但是聚类精度越低。因此，在实际调控中需要合理选择广义储能的聚类组数。

为确定最佳的聚类组数，本文设置了有效性指标，即

式中，n0为聚类组数；Dmin为聚类中心间距离的最小值；d(k)max为第k群中元素到聚类中心距离的最大值。

该聚类指标要求集群之间需要有较大的距离，避免聚类组数过多，同时集群内部需要有较小的距离，以提高聚类精度。该指标越大说明聚类效果越好。基于有效性指标的广义储能集群聚类流程如附图1 所示。

2 计及温度不确定性的配电网广义储能集群优化调控模型

2.1 配电网广义储能集群优化调控模型

2.1.1 目标函数

配电网中调度资源包括微燃机、风机、光伏及广义储能集群。以配电网运行成本最小为目标，考虑弃风弃光成本以及广义储能集群调度成本，建立目标函数F为

式中，CB、CG、Closs、Cwaste、Cac分别为从上级电网购电成本、微燃机运行成本、网损成本、弃风弃光成本及广义储能集群调度成本。

购电成本为

网损成本为

微燃机运行成本为

弃风弃光成本为

广义储能集群调度成本为

式中，T为调度时段总数；为购电电价；为从上级电网购电功率；为网损功率；NG为微燃机的数目；为微燃机i的出力；ai、bi为微燃机i运行成本系数；NWT与NPV分别为风机与光伏的数目；cWT与cPV分别为弃风与弃光成本系数；与分别为风机i与光伏i的预测出力；与分别为风机i与光伏i的实际出力；Nac为广义储能集群数目；cac为单位功率的用户补偿成本。

2.1.2 约束条件

1）潮流约束

配电网通常是以辐射状网络开环运行。根据文献[21]，考虑线路两端节点电压相位差较小，可采用改进型直流潮流，有

式中，Pij与Qij分别为线路ij传输的有功功率与无功功率；iV与iθ分别为节点i的电压幅值与相位；gij与bij分别为线路ij的电导与电纳。

线路ij的网损可表示为

式中，Pij,loss为线路ij的网损；Iij为线路ij的电流；rij为线路ij的电阻。

节点电压需在允许范围内，满足

式中，Vimin与Vimax分别为节点i允许电压的下限与上限值。

线路功率满足

式中，Sijmax为线路ij允许的最大传输功率。

2）机组运行约束

系统中微燃机运行需满足出力上下限约束、爬坡率约束，如式（29）～式（31）所示。

式中，QG,i为微燃机i的无功出力；PG,i,min与PG,i,max分别为微燃机i的最小与最大有功出力；QG,i,min与QG,i,max分别为微燃机i的最小与最大无功出力；与分别为微燃机向上与向下爬坡率限制。

风机、光伏的出力及负荷功率通常由前一天的预测数据给定。考虑弃风与弃光，风机与光伏的实际出力满足

式中，QWT,i与QPV,i分别为风机i与光伏i的无功出力；与φPV,i分别为风机i与光伏i的功率因数。

3）上级电网购电约束

为避免风机、光伏的波动对上级电网的产生运行，不考虑配电网潮流反供。配电网从上级电网购电功率满足

式中，BP、QB分别为上级电网向配电网传输的有功功率、无功功率；PBmin与PBmax分别上级电网向配电网传输的最小与最大有功功率；QBmin与QBmax分别上级电网向配电网传输的最小与最大无功功率。

4）广义储能集群调控约束

广义储能集群需满足等效荷电状态递推关系约束、等效荷电状态上下限约束、功率上下限约束，如式（14）～式（17）所示。为保证调控过程中用户的舒适度，相邻两时段室温变化不宜过大，广义储能集群等效荷电状态满足

式中，ΔESOCmax为相邻时段广义储能集群等效荷电状态变化最大值。同时，为保障广义储能集群下一优化时段的可调控量，集群在调控开始前与调控结束后，其等效荷电状态需满足

2.2 计及温度不确定性的广义储能集群分布鲁棒优化模型

根据式（14），广义储能集群模型与室外温度的变化密切相关。而在调控过程中，室外温度由预测给定，具有一定误差，实际的温度具有较大的不确定性，采用确定性优化模型，将难以保证调度的经济性，可能导致实际调控过程中广义储能集群等效荷电状态超出限定范围，对用户舒适度造成较大影响。因此，为满足用户舒适度要求，本文考虑室外温度不确定性，引入机会约束来描述约束被违反的概率，建立广义储能分布鲁棒优化模型。

2.2.1 室外温度概率分布模糊集构建

假设室外温度有m个不确定区间iO，如图2 所示，满足

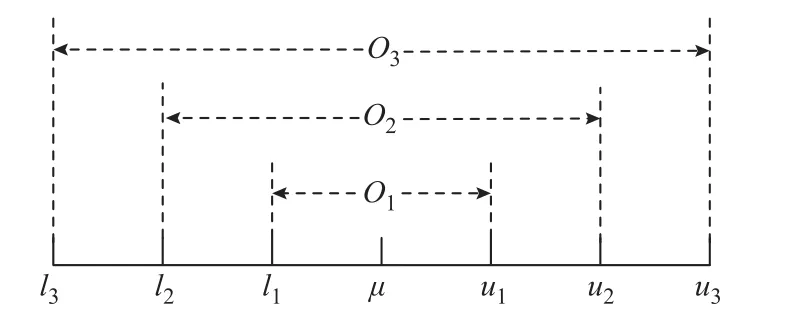
图2 室外温度不确定区间Fig.2 Outdoor temperature uncertainty range

式中，ξ为室外温度实际值；il与ui分别为第i个不确定区间的下限与上限；μ为室外温度预测值。

基于大量的历史数据，获取室外温度处于不同不确定性区间下的概率信息，进而构建室外温度概率分布模糊集P为

式中，EP为数学期望；ip为室外温度属于第i个不确定区间的概率；P为ξ的概率分布；P0(Om)为ξ基于的全部概率分布集合。

2.2.2 分布鲁棒机会约束构建及转换

以不确定变量ξ来表示室外温度实际值，引入分布鲁棒机会约束，则广义储能集群模型中式（14）与式（15）可转换为

式中，1-ε为机会约束的置信水平；λΣ、γΣ为广义储能集群的特征参数。

式（42）与式（43）表明了对于模糊集P中室外温度的全部概率分布，广义储能集群等效荷电状态满足上下限约束的概率不小于1-ε。

式（42）与式（43）可由统一形式表示为

文献[22]证明了式（44）可用条件风险价值（Conditional Value at Risk, CVaR）约束近似表示为

式中，τ为对偶变量；(x)+= max(x,0)。

CVaR 近似约束相较于原分布鲁棒机会约束更为保守，能够通过一定的线性决策规则转换为凸约束，实现模型的有效求解。同时，该约束具有更优的鲁棒性，对于越严重的约束违反行为施加的惩罚越大[23]，从而减小了违反约束的概率，保障了用户舒适度。

基于式（40）所构建的室外温度概率分布模糊集，文献[24]推导出CVaR 约束的线性等价表示形式为

式中，y与iχ均为对偶变量。

将式（42）与式（43）分别代入式（47），得到分布鲁棒机会约束近似线性不等式组，便于模型计算求解。

3 广义储能集群群内功率分配控制策略

根据变频空调的广义储能模型，其等效荷电状态表征了系统的储热量，描述了室内温度的实时变化。与用户舒适度密切相关。因此，为充分发挥各广义储能的调控潜力，保证用户舒适度以及调控公平性，本文以集群内各广义储能的等效荷电状态一致性最优为优化目标，即

式中，n为集群内广义储能的数量。该式表示了集群内所有时段广义储能等效荷电状态的方差和，其值越小表明等效荷电状态之间的偏差量越小。

集群内各广义储能需满足等效荷电状态递推关系约束、功率上下限约束、等效荷电状态变化率约束、剩余等效荷电状态约束、等效荷电状态上下限约束、总功率约束。其中等效荷电状态递推关系约束、功率上下限约束如式（10）～式（13）所示。等效荷电状态变化率约束、剩余等效荷电状态约束如式（36）与式（37）所示。

为减小室外温度不确定性的影响，满足用户舒适度，集群内各广义储能等效荷电状态的上下限可由分布鲁棒方法求得的该集群等效荷电状态最大最小值得到。等效荷电状态满足

各广义储能的总功率需满足

式中，Pac′Σ为广义储能集群的总功率需求。

同时为保证各广义储能的调控一致性，各广义储能等效功率需同时增加或减小，即满足

式中，Pacb,i与PacbΣ分别为广义储能i的基准功率与集群基准功率。

4 算例分析

4.1 算例参数设置

本文基于改进的IEEE 33 节点配电网络，对所提方法的有效性进行验证，系统的拓扑结构如附图2 所示。以一天24 h 作为调控时长，优化步长为15 min。系统在节点9、24、28 及33 处装接入微燃机组，其参数见附表1；节点17、22、32 处接入光伏，节点3、6、11、19 处接入风机，光伏与风机的功率因数均为0.95，光伏与风机出力以及负荷的预测基线如附图3 所示。从上级电网购电的最大与最小有功功率分别为3 MW 与0.5 MW；最大与最小无功功率分别为2.5 Mvar 与0 Mvar。购电电价及单位功率用户补偿成本见附表2，弃风、弃光成本为160 $/(MW·h)。节点电压上下限取为基准电压的1.1与0.9 倍。

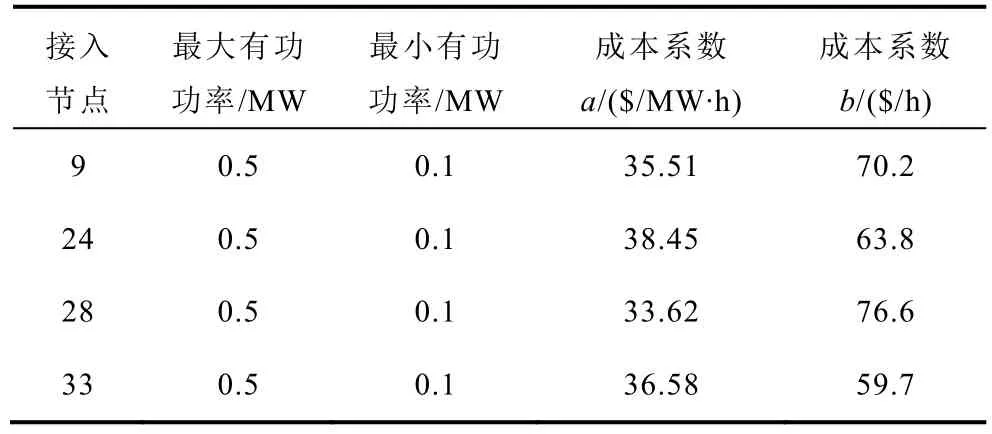
附表1 微燃机参数App.Tab.1 Micro gas turbine parameters

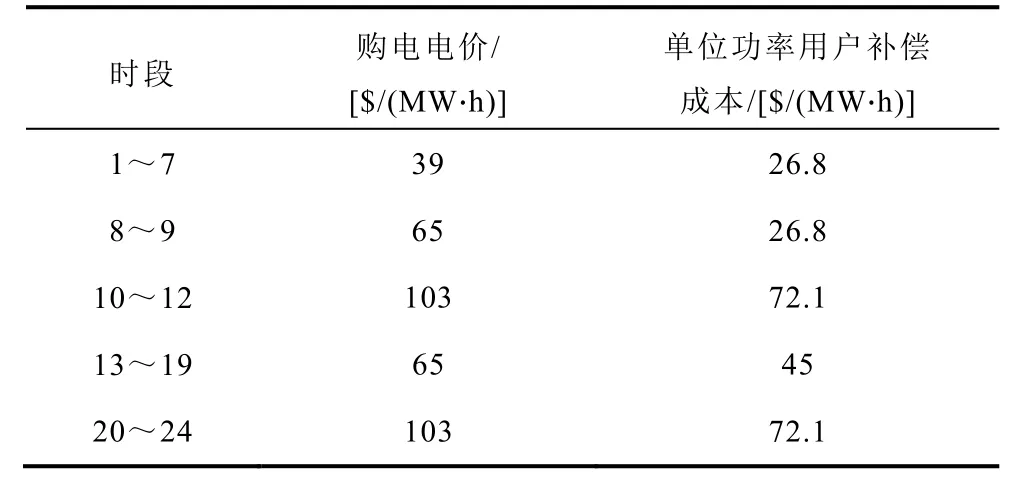
附表2 购电电价及单位功率用户补偿成本App.Tab.2 Electricity purchase price and user compensation cost per unit of power

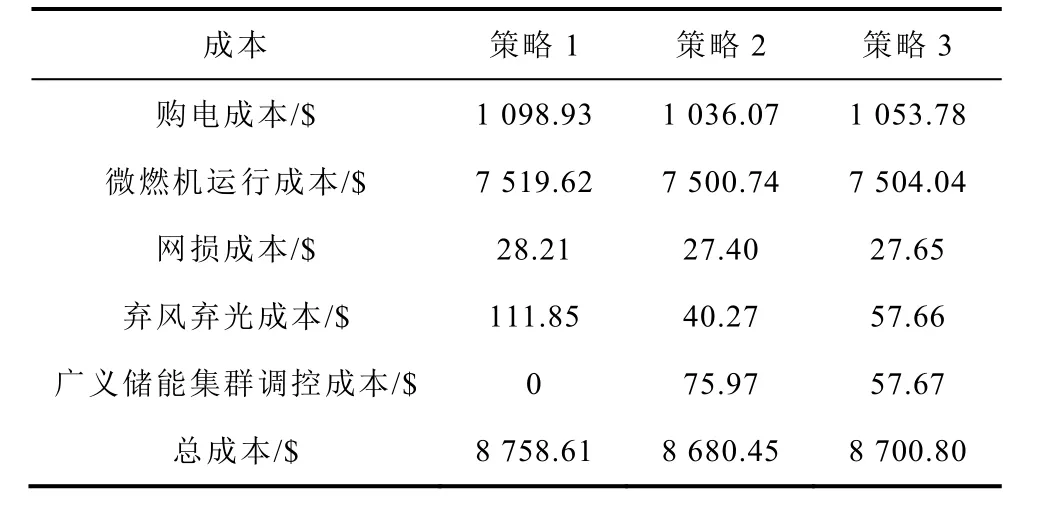
表1 三种优化策略下系统运行成本Tab.1 System operating cost under three optimization strategies

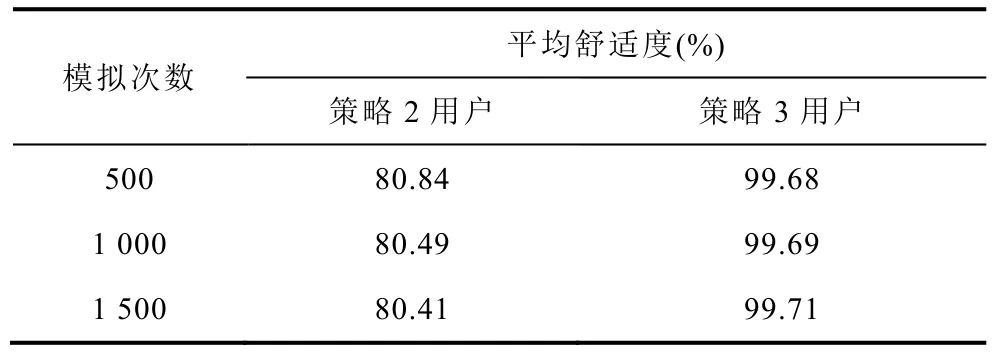
表2 蒙特卡洛模拟结果Tab.2 Monte Carlo simulation results

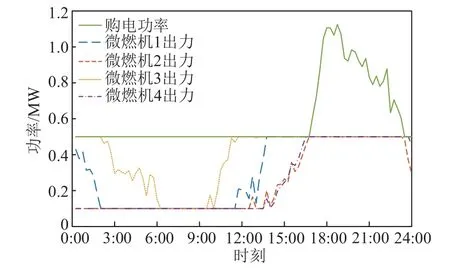
图3 策略3 微燃机出力及购电功率Fig.3 Micro-gas turbine output and power purchase under Strategy 3

变频空调的模型参数见附表3，相邻时段广义储能荷电状态变化最大值为0.125。采用计及有效性指标的k-means 聚类算法构建广义储能集群，其聚类结果见附表4。选择某地区夏季典型日温度曲线作为室外温度预测曲线，如附图4 所示。以室外温度预测值作为均值、1℃为标准差构建室外温度的正态分布函数，并基于此抽样得到10 000 组温度数据，从而构建室外温度概率分布模糊集P。为验证所提的方法的有效性，本文设置以下三种优化策略：①策略1：广义储能集群不可调控；②策略2：不考虑室外温度不确定性，采用广义储能集群确定性优化模型；③策略3：考虑室外温度不确定性，采用广义储能集群分布鲁棒优化模型，设置不确定性区间数量m为15，ε为0.001。

附表3 空调-建筑系统参数App.Tab.3 Air conditioning - building system parameters

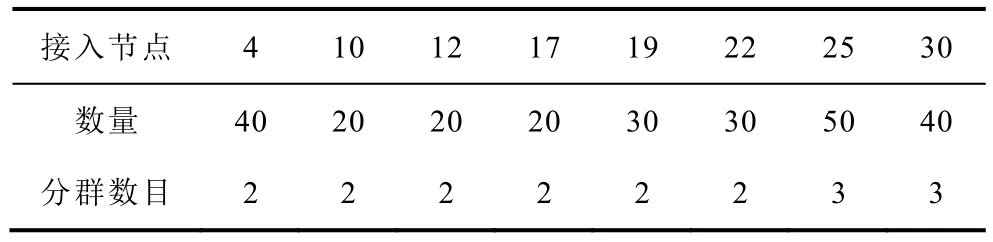
附表4 广义储能聚类结果App.Tab.4 Generalized energy storage clustering results

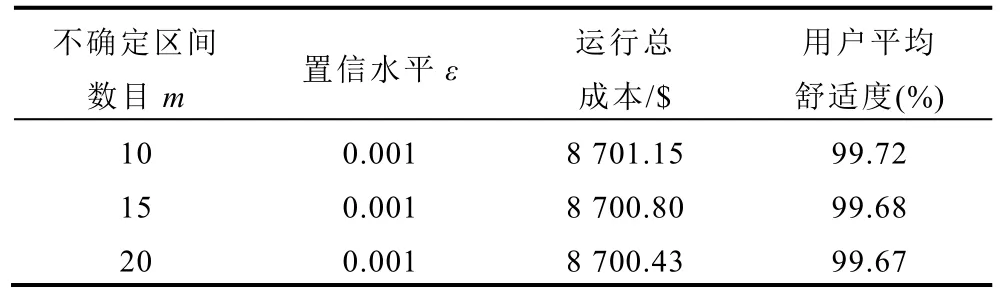
表3 不同不确定区间数目优化结果对比Tab.3 Comparison of optimization results for the number of different uncertainty intervals

表4 不同置信水平下优化结果对比Tab.4 Comparison of optimization results at different confidence levels

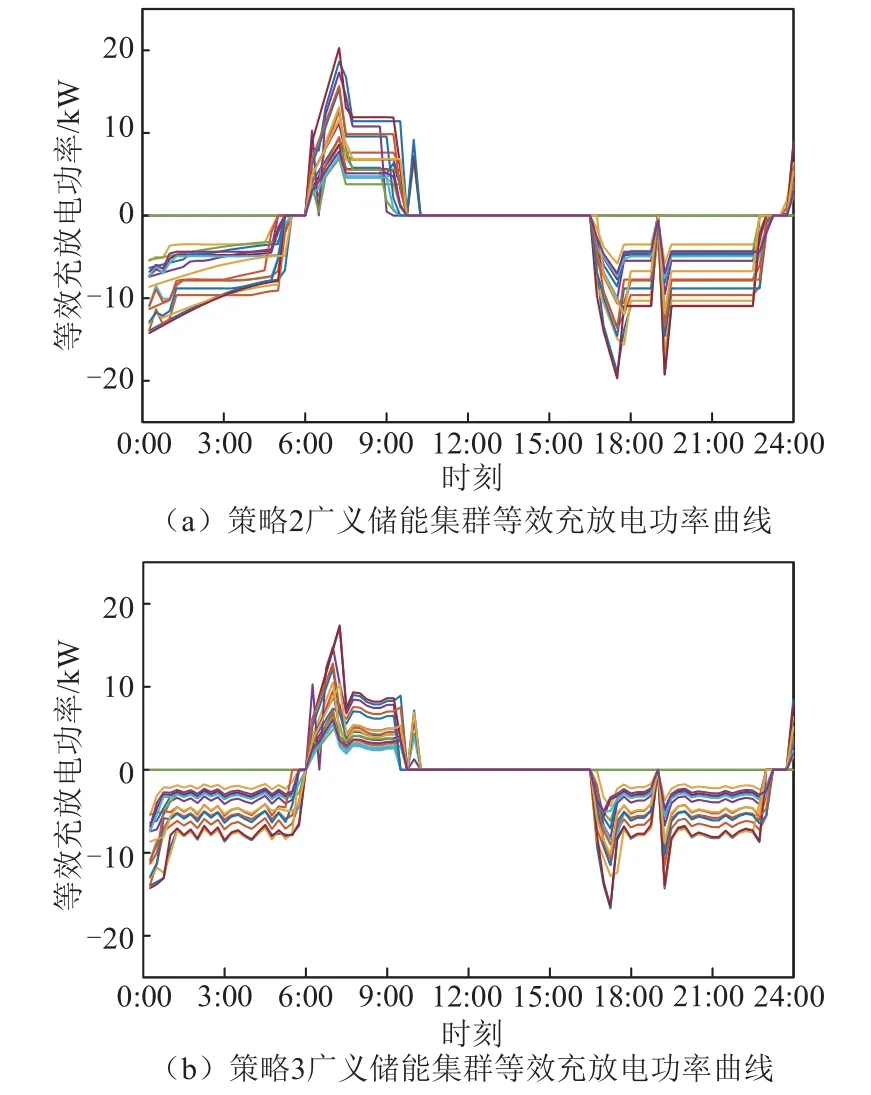
图4 广义储能集群等效充放电功率对比Fig.4 Equivalent charge and discharge power comparison of generalized energy storage clusters

本文的仿真环境为Matlab2018a，基于YALMIP调用Gurobi 求解器求解。

4.2 仿真分析

4.2.1 不同策略下广义储能集群调控结果分析

基于4.1 节的算例设置分别对策略1、2 和3 开展模拟仿真，求解出三种优化策略下系统的运行成本见表1。

由表1 可以看出，对比策略1 与策略2 和3，当广义储能集群不参与调控时，系统具有较高的弃风弃光量及网损，其运行总成本及各项成本均最高；当广义储能集群参与调控时，系统中增加了广义储能集群调控成本，但运行总成本减小，同时弃风弃光成本显著降低，网损成本有所减小，因此，调控广义储能集群能够有效地降低电网运行成本，避免弃风弃光。同时，通过调控广义储能集群，使得部分功率能够就地平衡，避免了功率的传输，降低了系统的网损。对比策略2 与3，策略3 中广义储能集群调控成本较低，而其余各项成本及总成本均较高，其原因为策略3 考虑了室外温度不确定性，减小了广义储能集群的功率调控范围及灵活度，以避免其等效荷电状态超出约束范围，保障了用户舒适度，调控过程相对保守。

策略3 各微燃机出力以及系统的购电功率如图3 所示。由图3 可知，在0:00—6:00 时段，风电出力较大，同时负荷水平逐渐降低，微燃机出力逐渐减小。在6:00—9:00 时段，光伏出力急剧增加，此时负荷水平较低，为满足负荷需求，各微燃机出力维持在最低水平，同时系统需要弃风弃光。在9:00—16:00 时段，负荷功率上升到较高水平，各微燃机出力也逐渐增加，由于此时段售电电价较高，系统购电功率维持在最低水平。在16:00—24:00 时段，负荷功率维持在较高水平，各微燃机出力达到最大，而光伏出力逐渐下降，为满足负荷需求，配电网需增加购电功率，至19:00 时购电功率达到最大，此时光伏出力下降为0，而后由于负荷功率逐渐降低及风电出力逐渐，购电功率逐渐减小。

策略2 和3 各广义储能集群的等效充放电功率对比如图4 所示。集群等效充放电功率由各集群实际功率减去集群不调控时的基准功率所得。三种策略下广义储能集群的等效荷电状态对比如图5 所示。由图4 和图5 可以看出，在00:00—6:00 时段，用户补偿成本较低，为降低微燃机的运行成本，广义储能集群功率减小，等效于向电网放电，此时集群的等效荷电状态逐渐减小，储热量降低。在6:00—9:00 时段，光伏出力突增，为减小系统弃风弃光，广义储能集群功率增加，等效于充电，此时集群的等效荷电状态逐渐增大，储热量升高。在9:00—16:00 时段，由于该时段用户补偿成本较高，广义储能集群以基准功率运行，其等效荷电状态保持在初始设定水平。在16:00—24:00 时段，光伏出力降低，系统购电功率增加，为减小购电成本，广义储能集群向电网放电，其等效荷电状态减小，而后在23:00时集群转为充电，在调控结束时，等效荷电状态保持在初始水平，以便下一天的调控。

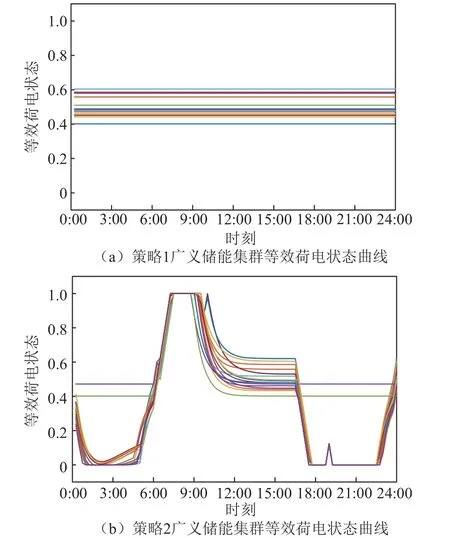
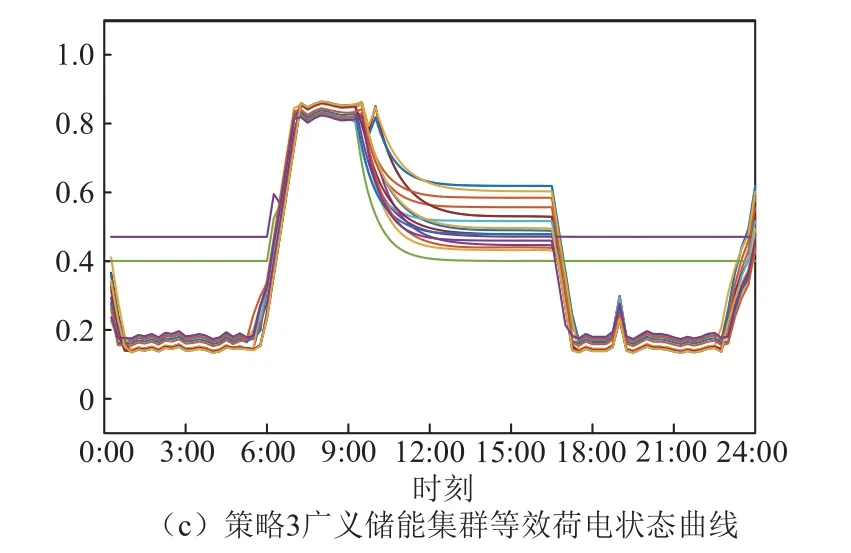
图5 广义储能集群等效荷电状态对比Fig.5 State-of-charge comparison of generalized energy storage clusters

对比图4 与图5 可以看出，策略2 中广义储能集群的等效充放电功率较大，在7:00—9:00 时段与1:00—6:00、17:00—23:00 时段，其等效荷电状态分别到达约束上限与下限；而在策略3 中，广义储能集群的等效充放电功率相对较小，在7:00—9:00时段与1:00—6:00、17:00—23:00 时段，其等效荷电状态分别为0.85 与0.15，离约束上下限具有一定裕度，以避免室外温度不确定性的影响。同时，在调控周期内，各集群的等效荷电状态变化速率较为平缓且趋势一致，保障了用户的舒适度以及调控的公平性。

4.2.2 优化策略鲁棒性分析

为验证分布鲁棒优化方法的优化效果，本节基于4.1 节构建的室外温度概率分布模糊集，抽样得到室外温度曲线作为实际值，并做蒙特卡洛模拟试验，分别统计在策略2 与策略3 的调控方案下，广义储能集群等效荷电状态上下限约束违反的时段数，进而计算用户平均舒适度。

定义用户平均舒适度为

式中，Save为用户平均舒适度；NM为蒙特卡洛模拟试验次数；为广义储能集群j在第i次蒙特卡洛模拟中t时刻等效荷电状态的越限状态，当等效荷电状态越限时，其值为0，反之，其值为1。

分别模拟500 次、1 000 次以及1 500 次，其结果见表2。可以看出，策略3 用户平均舒适度较策略2 有明显的提升，其等效荷电状态基本在约束范围内，违限次数较小，具有较好的鲁棒性，极大地提高了用户舒适度。随着模拟次数的增加，策略2用户平均舒适度有所下降，策略3 用户平均舒适度有所上升，基本维持在99.7%左右。在某一次模拟下广义储能集群等效荷电状态变化对比如图6 所示，可以看出，在策略2 的调控方案下，集群等效荷电状态在较多时段超出约束范围，最小达到-0.2，极大地影响了用户舒适度，而策略3 中，集群等效荷电状态均在约束范围内，保障了用户舒适度。

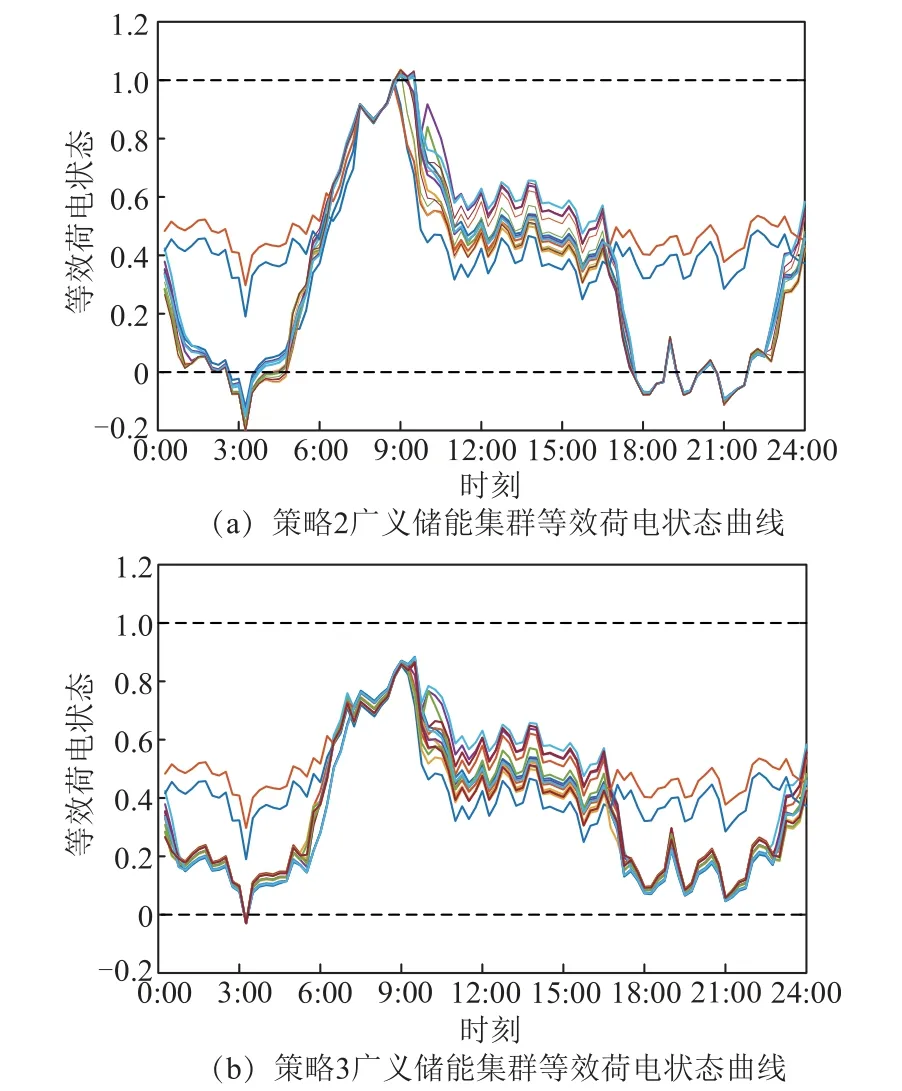
图6 某一次模拟下广义储能集群等效荷电状态对比Fig.6 Comparison of the equivalent state of charge of generalized energy storage cluster under a simulation

为验证不同不确定区间数目m与置信水平ε对广义储能集群优化效果的影响，分别求解出m为10、15、20，ε为0.005、0.01、0.02 时，运行总成本以及用户平均舒适度，结果见表3 与表4。

由表3 可以看出，随着不确定性区间数目的增加，室外温度的不确定性信息增加，系统运行总成本减小，而用户平均舒适度降低，优化保守性下降。由表4 可以看出，随着置信水平的增加，广义储能集群等效荷电状态违反约束的概率增加，系统运行总成本减小，但用户平均舒适度降低。

4.2.3 广义储能集群群内功率分配结果分析

以接入节点4 的广义储能集群2 为例，分析广义储能集群群内功率分配策略的效果，该集群中广义储能的数量为15，优化结果如图7 所示。

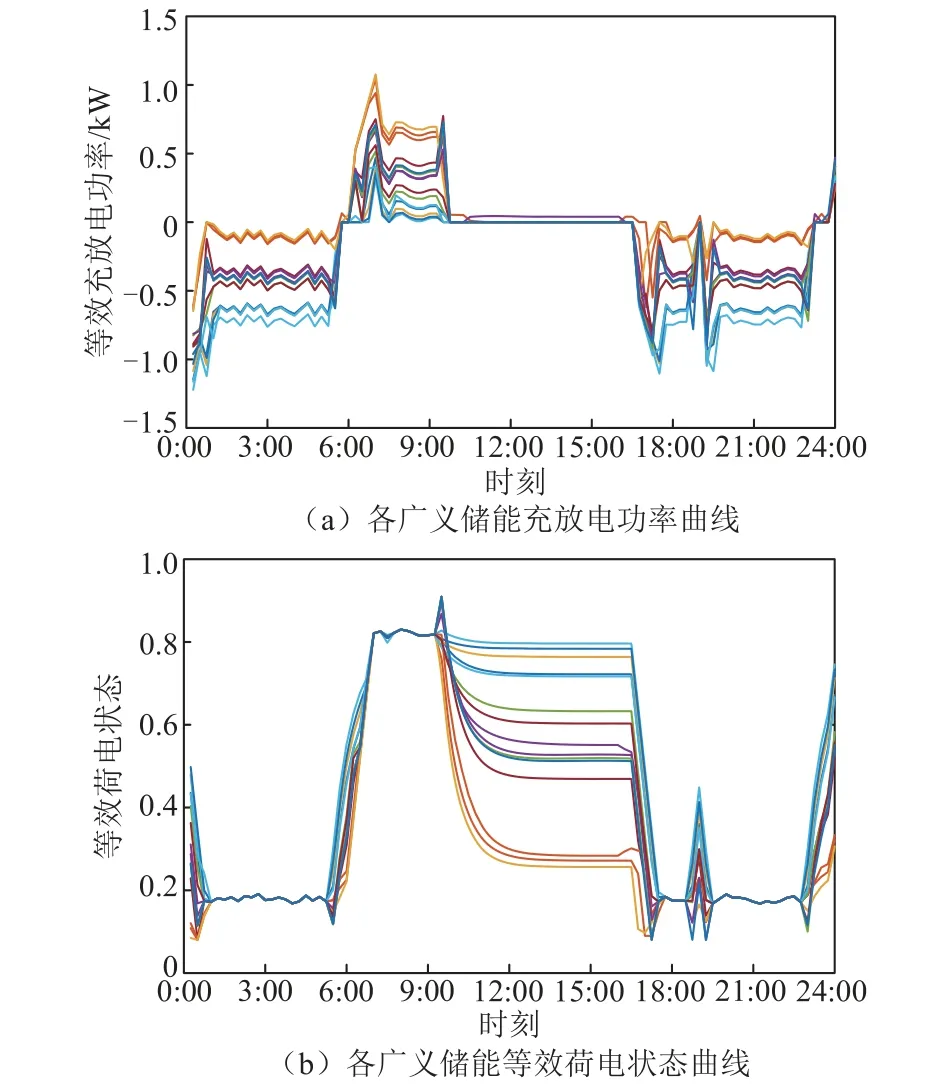
图7 广义储能集群群内优化结果Fig.7 Intra-group optimization results of generalized energy storage clusters

由图7 可知，经过功率分配后，集群内各广义储能充放电功率有所差别，但总体变化趋势相同。各广义储能的等效荷电状态趋于一致，从而保障了调控的公平性。同时，其等效荷电状态的最大、最小值距离上、下限边界具有一定裕度，避免了因室外温度不确定性导致等效荷电状态超出约束限制，影响用户舒适度。

4.2.4 广义储能聚类结果分析

同样以接入节点4 的广义储能集群2 为例，分析广义储能聚类分群结果的有效性。假设该集群不参与调控，集群中各广义储能的等效荷电状态将保持其初始状态不变，在此场景下，分别计算广义储能等效集群的功率与各广义储能的总功率，结果如图8 所示。

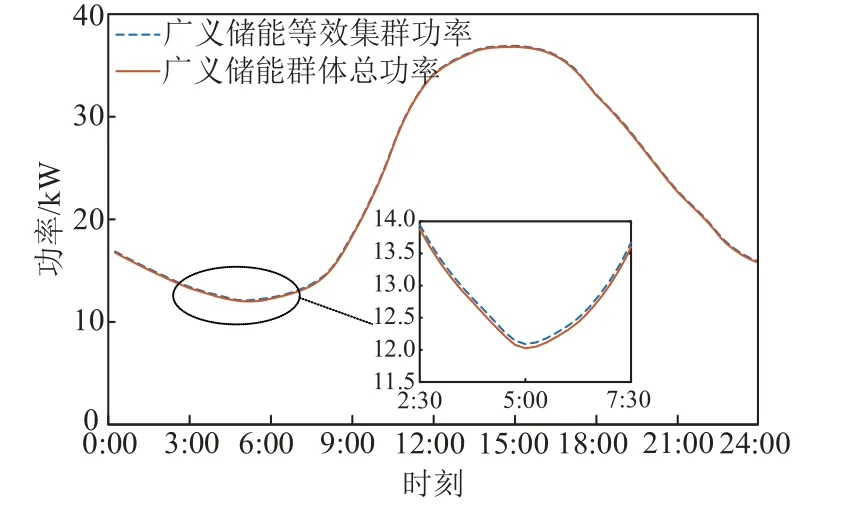
图8 广义储能等效集群功率与广义储能群体总功率对比Fig.8 Comparison of generalized energy storage equivalent cluster power and generalized energy storage cluster total power

由图8 可知，聚类后的广义储能集群与广义储能群体运行特性十分相近，最大相对误差仅为0.54%。因此，基于有效性指标的广义储能集群聚类方法在降低调控复杂度的同时，能够有效保证聚类精度。

5 结论

本文建立了变频空调广义储能分层调控框架，在广义储能集群调控层面，提出计及温度不确定性的配电网广义储能集群分布鲁棒优化策略；在广义储能群内调控层面，提出广义储能集群群内功率分配策略。仿真算例验证了本文调控策略的有效性，得出以下结论：

1）变频空调具有类似储能电池的调控特性，将其等效为广义储能参与调控，能够有效降低配电网运行成本，减小系统网损，提高可再生能源消纳水平。

2）所提的广义储能集群分布鲁棒优化策略，可有效避免由室外温度不确定性导致室内温度越限的问题，保障用户舒适度。

3）所提的广义储能集群群内功率分配策略，在满足用户舒适度的前提下，可实现群内各广义储能等效荷电状态变化一致，保障调控的公平性。

本文研究了室外温度不确定性对广义储能集群调控的影响，而日照强度、用户使用行为等因素同样会对广义储能的运行状态产生影响，计及室外温度、日照强度及用户响应行为等多重不确定性的广义储能调控问题将是下一步研究的重点。

附 录

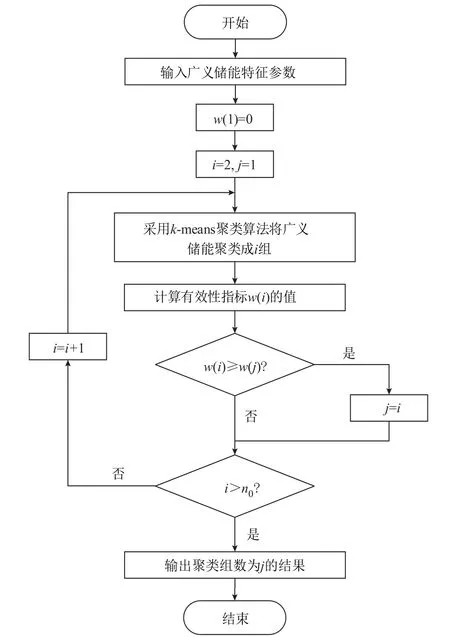
附图1 广义储能集群聚类流程App.Fig.1 Generalized energy storage cluster clustering flowchart

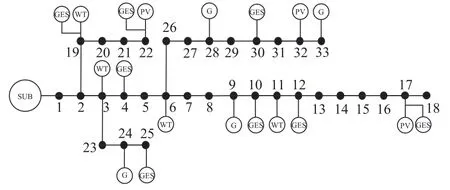
附图2 改进IEEE 33 节点拓扑图App.Fig.2 Improved IEEE 33 node topology

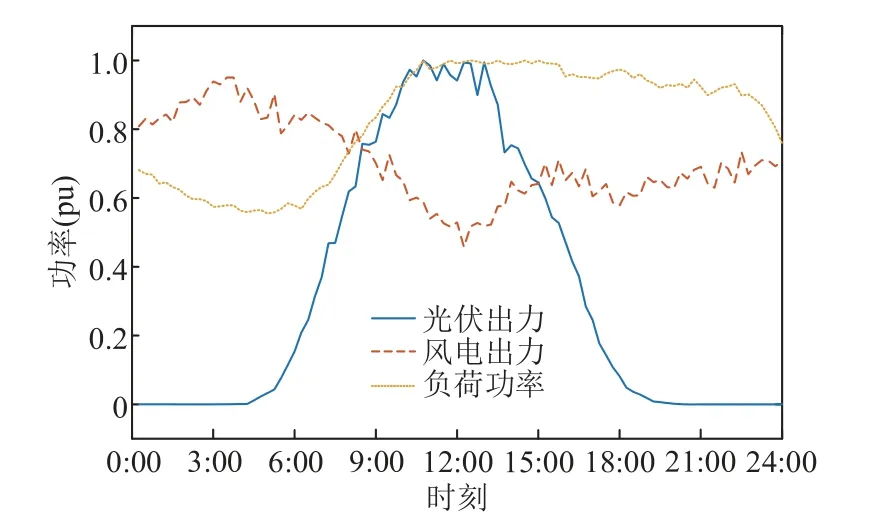
附图3 光伏、风机出力及负荷预测曲线App.Fig.3 Prediction curves of photovoltaic output, wind turbine output and load

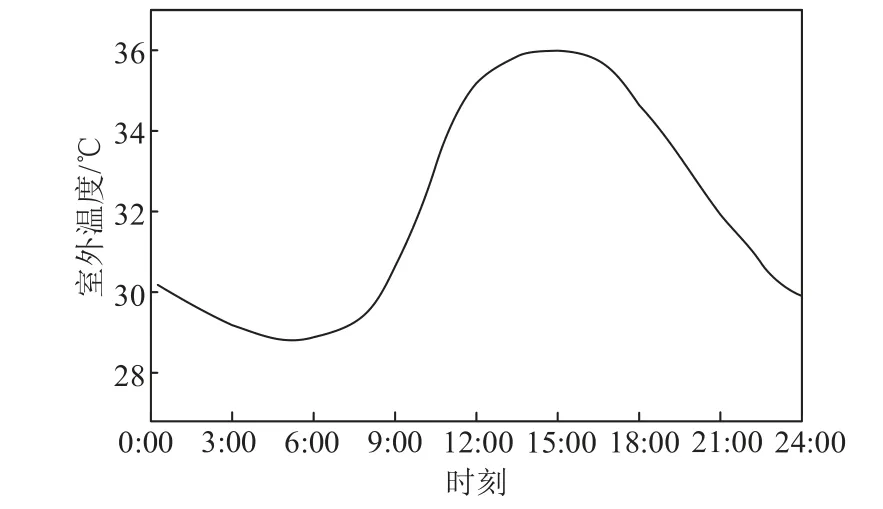
附图4 室外温度预测曲线App.Fig.4 Outdoor temperature prediction curve