一种考虑动态磁滞效应的高效稳定时域有限元计算方法

魏 鹏 陈 龙 贲 彤 井立兵 张 献

（1.三峡大学电气与新能源学院 宜昌 443002 2.湖北省微电网工程技术研究中心（三峡大学） 宜昌 443002 3.省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130）

0 引言

时域有限元方法广泛应用于电工装备的运行状态预测与损耗评估之中[1]，准确预测电机、变压器等电工装备的时域暂态损耗分布特性不仅对降低设备能耗、改善局部过热具有重要意义，同时考虑损耗对暂态磁场求解的反馈作用，对进一步分析电工装备的瞬时功率平衡、暂态励磁特征等电磁特性至关重要[2-4]。

目前，对于电工装备铁心损耗的有限元计算方法可大致分为两类：一是基于场计算结果的后处理方法，该类方法利用Steinmetz 损耗模型或Bertotti统计学损耗分离理论对仅单值非线性磁场的计算结果进行后处理，得到每一个单元的损耗，最终进行积分得到电工装备整体的损耗[5-7]。这一类方法主要用于对电机或变压器的损耗进行频域分析，并通过傅里叶变换来分析含有谐波激励时的铁心损耗。Ansys 公司D.Lin 等基于等效椭圆环思想，将上述方法进行了时域瞬时功率损耗计算扩展[8]。该方法的优势在于在损耗计算过程中无需迭代，在磁路简单的结构中具有较好的精度，但由于没有考虑铁心磁滞、涡流损耗、剩余损耗等效动态磁场对铁心中磁场分布的反馈作用，在电机等复杂磁路电工装备的损耗计算中将带来较大误差。另一类铁心损耗计算方法则是在时域有限元分析中，考虑动态磁滞效应对每一瞬时的功率损耗进行精确求解[9-10]。这一类方法可最大限度地模拟铁心的真实磁化过程，在处理含有磁通密度波形畸变工况下的损耗计算问题时具有较高精度。同时，在考虑铁心动态磁滞效应后，铁心中动态磁滞回线波形的精确模拟可在时域中对励磁电流的波形进行实时反馈，进而可对电机或变压器中暂态运行特性进行有效预测。因此，电工装备损耗的精确预测与运行状态的有效评估都离不开在时域有限元分析时对动态磁滞特性的影响的考虑。

然而，目前在有限元分析中常用的磁滞模型，如J-A 模型[11-13]、Preisach 模型[14-17]等均是与磁化速率无关的磁滞模型，并不能直接考虑电机或变压器叠片宏观涡流损耗与剩余损耗等动态因素对铁心磁场分布的影响。为此，需要进一步将二者的等效动态磁场考虑到有限元的计算方程之中。传统方法是将动态效果等效为电导率乘以磁矢位A对时间的一阶导数，但该种等效仅适合均匀实心区域涡流路径的求解，并不适合叠片铁心结构[18-19]。对于铁心叠片结构，进行实际三维建模将会带来无法承受的计算成本。为此，E.Dlala 等提出了一种耦合一维叠片有限元方法的二维时域有限元计算方法[20-21]。在叠片维度，忽略边缘效应，认为磁通密度仅是叠片厚度方向上的函数，进而仅需要求解一维有限元方程，即可得到叠片的涡流损耗等效磁场。然而，该方法实质上是在二维有限元计算中嵌套了一维有限元程序，仍具有较高的求解难度。为了对上述求解方法进行简化，目前常采用Bertotti 模型的变形形式，即在耦合静态磁滞模型的过程中，通过耦合等效微分磁阻率来考虑涡流损耗磁场与剩余损耗磁场的效果，该方法避免了一维有限元的求解，在一定程度上大大简化了计算，但在每次迭代过程中仍需更新磁阻率和刚度矩阵，导致计算效率低下[22-23]。因此，在进一步求解含有等效磁阻率的方程时，需要进一步耦合非线性磁场计算中的固定点迭代技术。在仅考虑静态磁滞模型的有限元计算中，固定点迭代方法已经取得了较好的收敛效果与计算速度[24-26]，并已在目前的商业软件中取得了较好的计算效果。然而，在引入涡流损耗磁场与剩余损耗磁场后，收敛将难以得到保证，特别是在计算至磁通密度零点附近时间步时算法极易发散，分析其原因主要是涡流损耗、剩余损耗等效动态磁场的介入改变了固定点法中磁通密度与磁场强度的收敛过程，使得传统微分磁阻率的定义无法准确描述收敛路径的斜率，计算得到微分磁阻率过低导致考虑动态磁滞效应的有限元方程求解不收敛。

为解决在考虑动态磁滞特性的时域有限元计算难以收敛的问题，本文提出一种基于等效磁阻率的固定点迭代求解策略，进而提出一种耦合动态磁滞特性的时步有限元分析方法。首先，为了获得电工钢片的动态、静态磁滞特性，基于爱泼斯坦方圈法搭建了一维磁特性测量系统；其次，考虑到逆Preisach模型可以考虑磁化历史具有较高的计算精度，同时在耦合有限元计算时易于数值实现的特点，本文构建了基于参数化解析一阶回转曲线的逆 Preisach模型，并进行了参数辨识；再次，分析了涡流损耗和剩余损耗对算法收敛特性的影响，提出基于等效磁阻率的固定点迭代策略，并在有限元迭代过程中加入松弛因子保证稳定性；最后，以爱泼斯坦方圈为例，进行了考虑动态磁滞效应的时域有限元分析，求解了瞬时功率损耗特性，并进行了实验对比验证。结果验证了本文所提方法的准确性、高效性与稳定性。

1 准静态与动态磁滞特性测量

为建立磁滞模型及验证有限元计算准确性，基于 IEC 60404—2 标准建立了一维磁性能测量平台，对牌号为B30P105 的取向硅钢片进行准静态与动态磁滞特性测量。电工钢片一维磁特性测量平台如图1 所示，该平台包括宽频功率放大器、电压前置放大器、爱泼斯坦方圈、多功能数据采集卡和 LabVIEW 控制系统。本实验采用的硅钢片规格及测试条件见表1。分别设定正弦交流电压激励的频率为5 Hz 与50 Hz，测量得到准静态磁滞回线和50 Hz 动态磁滞回线，结果如图2 和图3 所示。

表1 硅钢片规格及测试条件Tab.1 Specifications and test conditions of silicon steel sheets

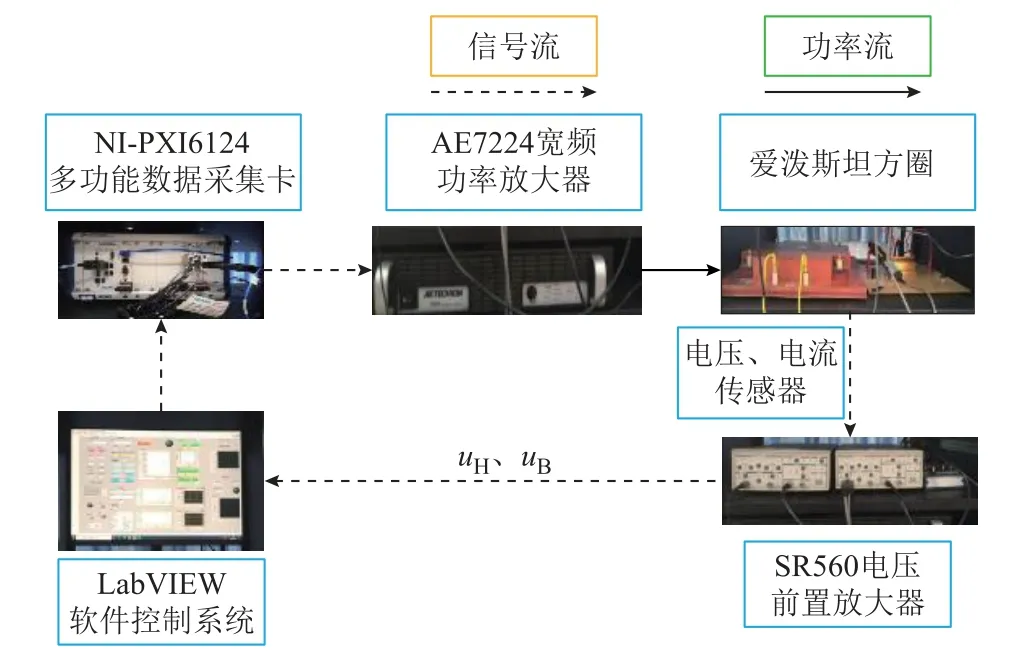
图1 电工钢片一维磁特性测量平台Fig.1 Measuring platform for 1-D magnetic propertiesof electrical steel sheets

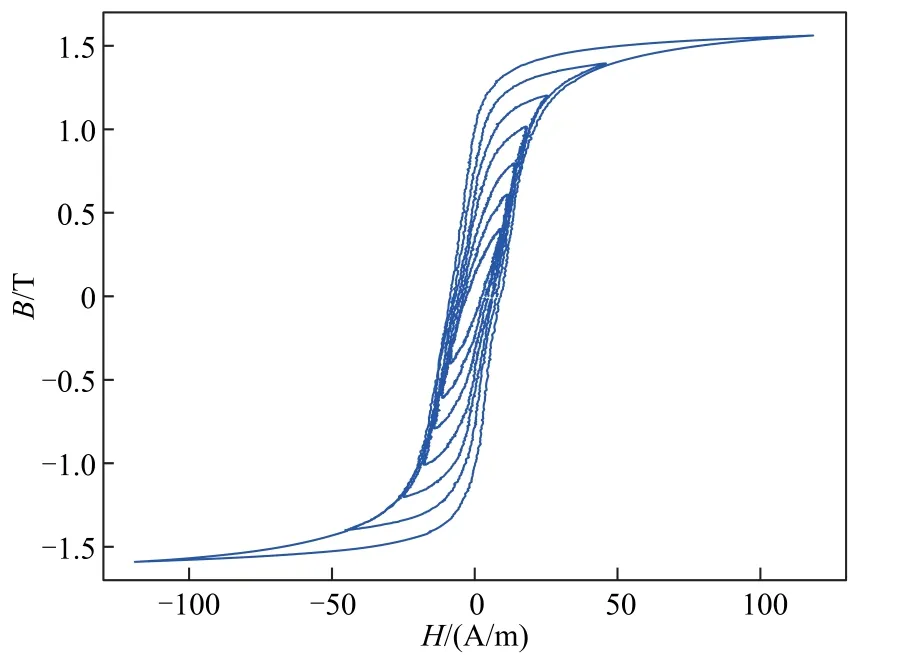
图2 5 Hz 准静态磁滞回线测量结果Fig.2 Measured quasi-static hysteresis loop (5 Hz)

图3 50 Hz 动态磁滞回线测量结果Fig.3 Measured dynamic hysteresis loop (50 Hz)

2 静态逆Preisach 磁滞模型的构建

本文采用离散形式的静态逆Preisach 磁滞模型描述硅钢片的磁滞特性，该模型采用一种一阶回转曲线（First Order Reversal Curves, FORCs）的解析计算方法，并基于少量准静态磁滞回线测量数据实现解析式的参数辨识，从而构造出辨识逆Everett 函数所需的一阶回转曲线，并进一步建立静态逆Preisach 磁滞模型。解析一阶回转曲线构造示意图如图4 所示：一条起始于准静态极限磁滞回线下降支的一阶回转曲线R-P-N-T，该曲线起点为回转点R，极限磁滞回线上升支Ha和下降支Hd交汇于顶点T。该一阶回转曲线构造时需首先确定极限磁滞回线在回转点R 处宽度ΔHrev和R 点与T 点的垂直高度ΔBrev为

图4 解析一阶回转曲线构造示意图Fig.4 Construction ofanalytical first order reversal curve

图4 中一阶回转曲线上点P 所在磁通密度为BP，磁场强度HP的计算式为

式中，ΔHout为极限磁滞回线在高度为BP处的宽度；x表征不同的P 点在一阶回转曲线上的相对位置，定义为

a、b、c为待拟合的模型参数。当满足a＞0，0＜b＜1，c＞0 等条件时，可使得一阶回转曲线斜率始终为正且不会超出最大极限磁滞回线。同时，以上模型参数与回转点R 在下降支上的位置有关，此处定义位置系数β为

式中，ΔBout为最大环磁滞回线的高度。

参数a、b、c可表示为β的多项式，即

式中，y为多项式系数向量。

以上多项式系数通过准静态磁滞回线测量数据进行辨识，由于对称性，辨识过程仅需要磁滞回线的上升支。逆Everett 函数值可利用上升支一阶回转曲线Hforc通过式（7）计算。

磁通密度幅值为Bm的同心磁滞回线上升支可通过逆Everett 函数进行插值运算得到。

辨识程序中一共使用9 条磁滞回线，将每条磁滞回线上升支根据磁通密度均匀等分为50 个点。基于式（7）、式（8）可得到由一阶回转曲线计算磁滞回线的数值关系，进而建立适应度函数F为

式中，Hmeas、Hcal分别为磁滞回线磁场强度的测量值和计算值；Bki为辨识程序中第k条磁滞回线上第i个点的磁通密度值。采用遗传算法基于适应度函数进行参数寻优，结果见表2。获得全部参数后，采用该解析式模拟所需一阶回转曲线数据，进一步可计算逆Everett 函数E(bu,bv)，通过解析一阶回转曲线辨识的逆Everett 函数如图5 所示。

表2 B30P105 型电工钢片多项式参数辨识结果Tab.2 The identified polynomial parameters of B30P105 elctrical steel sheet

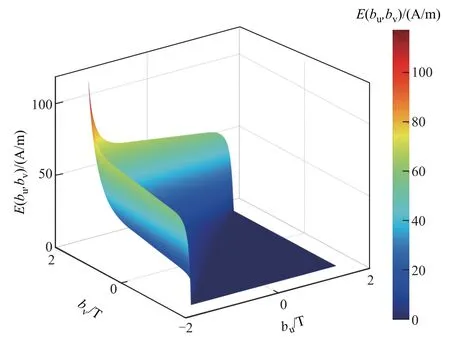
图5 通过解析一阶回转曲线辨识的逆Everett 函数Fig.5 Inverted Everett functionidentified by analytical first order reversal curves

通过上述逆Everett 函数辨识结果，可计算出一个周期内不同磁通密度下电工钢片的静态磁滞回线。B30P105 型取向硅钢的准静态磁滞回线实验结果和模型计算结果对比如图6 所示，可以看出，本文所构建的逆Preisach 磁滞模型具有一定的全局意义，可准确模拟不同磁通密度幅值下的准静态磁滞回线，为进一步考虑动态磁滞特性的有限元计算提供了可靠的模型基础。

图6 准静态磁滞回线测量值与计算值对比Fig.6 Comparison between measured and calculated quasi-static hysteresis loops

3 考虑动态磁滞特性的时域有限元方法

3.1 动态磁场的表征方法

Bertotti 基于磁畴理论和统计学原理提出损耗分离理论，将铁磁材料单位体积的总损耗Ptot分为磁滞损耗Phys、涡流损耗Peddy和异常损耗Pexc三项。即

式中，σ为材料的电导率；d为硅钢片厚度；S为横截面积；G为无量纲耦合常数，G=0.135 6；V0为与材料内部磁性单元有关的统计参数，同磁通密度幅值Bm相关，可通过不同频率下的磁滞回线实验数据拟合得到。

磁场损耗W与B、H之间的关系为

将式（11）代入式（10）可得动态磁场表达式为

式中，Htot、Hhys、Heddy、Hexc分别为动态磁场总磁场强度、静态磁滞磁场强度、涡流磁场强度、异常磁场强度；δB为符号函数，δB=sign(dB/dt)=±1。然而，由于较强的非线性特征，上述磁场难以直接在有限元分析中进行迭代耦合计算，需进一步研究其有限元迭代形式。

3.2 动态磁滞特性在有限元中的直接耦合形式

基于后向差分法，总磁场强度的三个分量的时域离散形式为

式中，t为时间步；Δt为步长间隔；vh为静态磁滞微分磁阻率，定义为

相关麦克斯韦磁场方程为

结合方程式（13）～式（19）可得基于矢量磁位A的控制方程为

式中，ve为等效磁阻率，表达式为

3.3 基于等效磁阻率的固定点迭代策略

固定点法通过将非线性磁滞关系分为线性和非线性两部分，通过在迭代过程内不断修改非线性部分以达到收敛，在解决磁滞非线性问题中具有较好的收敛性。为此，本文考虑将固定点迭代技术引入考虑动态磁滞特性的有限元迭代过程之中，在考虑静态磁滞特性的基础上，引入考虑动态磁场分量影响的等效磁阻率，采用式（21）中等效磁阻率代替传统固定点法的微分磁阻率vFP。应用固定点技术，总磁场强度Htot和磁通密度B的非线性关系可表示为

式中，R为类磁化余量。

结合麦克斯韦方程，可得控制方程为

在二维求解域Ω中，将方程式（23）展开为离散形式为

式中，N为离散单元的基函数。将方程式（24）改写为矩阵形式，即

式中，S为刚度矩阵；A为磁矢位向量；Y为电流区域系数向量；I为绕组电流向量；G为余量R的旋度矩阵。该方法中，涡流损耗等效磁场和剩余损耗等效磁场表达在类磁化余量R的计算中。通过这种方式，不需要大幅改动有限元方程，使得算法流程更简洁，同时，将动态特性考虑在余量中，便于在以后的工作中对涡流和剩余损耗计算模型的改进与修正。而且，在每一时刻的迭代过程，仅需计算一次等效磁阻率ve和刚度矩阵S，显著提升了计算效率。

为保证固定点算法收敛，磁阻率v应满足式（26）的必要条件[25,27]。

在传统固定点法中，所有网格单元采用统一的磁阻率，即

式中，vmin、vmax分别为磁滞回线上斜率最小值与最大值。该方法称为GCM（global-coefficient method）。显然，采用式（27）计算的磁阻率总能满足算法收敛的必要条件。然而，GCM 采用统一的磁阻率导致计算时间过长，需采用更具效率的微分磁阻率进行迭代，微分磁阻率vFP定义为

式中，dHtot、dB分别为磁场强度和磁通密度的差分。

对于标量磁滞模型，二维电磁场量间的关系可通过取模值降阶为一维问题。如图7 所示，蓝色实线表示静态磁滞回线，蓝色虚线表示动态磁滞曲线，曲线L 为固定点迭代过程中动态磁滞磁场Htot与磁通密度B的轨迹。由于磁场分量Heddy、Hexc的计算是基于磁通密度B的后向差分对时间的偏导数，因此，该曲线L 起始于t时刻静态磁滞回线上的点P1，止于t+1 时刻动态磁滞回线上点P3。显然，由于涡流损耗和剩余损耗的影响，曲线L 的斜率明显不同于动态磁滞回线的斜率，在磁通密度的零点附近，两者相差很大。传统的固定点迭代法采用式（28）来计算微分磁阻率vFP，由于只考虑到动态磁滞磁场的轨迹，其计算结果偏小，往往不满足收敛的必要条件，在迭代计算中算法极易发散。相反，在本文所提式（21）中等效磁阻率ve的计算考虑了涡流损耗和剩余损耗的等效磁场，反映了铁心动态磁滞损耗对迭代过程的影响大小，可准确估计动态B-Htot轨迹L 的斜率，从而保证迭代过程稳定收敛。在有限元程序中ve根据前两个时间点的结果进行估算，即

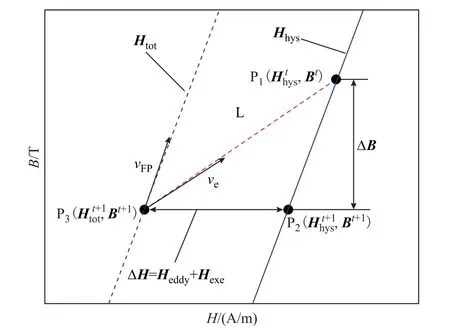
图7 动态磁滞收敛路径示意图Fig.7 Schematic diagramof dynamic hysteresis convergence path

3.4 考虑动态磁滞特性的场-路耦合有限元分析

鉴于电机、变压器等大多数电气设备工作于50 Hz正弦交流电压激励下，为反映动态磁场和电压源的相互作用，需在时域有限元分析中进行“场-路”耦合。由于爱泼斯坦方圈实质可看作一台等比的空载变压器，可以满足对变压器铁心损耗分析的需要。为验证本文所提方法的有效性，本文以爱泼斯坦方圈为例构建了二维有限元计算模型。

在模型的计算过程中，以50 Hz 正弦交流电压作为激励，从电路角度分析，不考虑励磁线圈漏磁和匝间电容，则端口电路方程为

式中，U为激励电压；Uin为绕组上的感应电动势；r为线路电阻；I为励磁电流。对于一阶三角形单元，Uin的计算式为

式中，Φ为绕组磁通；Nc为线圈匝数；Sc为绕组截面积；Ωc为电流区域；se为单元面积；lz为二维求解系统纵向深度；Ae为单元节点磁矢位。将式（31）代入式（30）得到

式中，U为激励电压向量；r为支路电阻矩阵。采用Crank-Nicolson 差分格式，将式（25）、式（32）联立求解。

通过求解方程式（33）得到磁矢势向量，然后根据B=∇×A计算出每个单元的磁通密度大小。如果计算结果未达到收敛条件eB=∣Bi+1-Bi∣＜Bε（相对残差阈值一般取εB= 1× 1 0-5），则通过磁滞模型计算静态磁滞磁场Hhys、涡流磁场Heddy、剩余损耗磁场Hexc，进而计算总磁场强度Htot，并通过松弛因子λ对Htot进行修正。

式中，i为迭代次数。若磁通密度B相邻迭代误差满足收敛条件，则判断是否达到最大时间步，若t=tmax，则停止迭代，输出全部计算结果，否则跳转至下一时间步。整个有限元迭代过程如图8 所示。

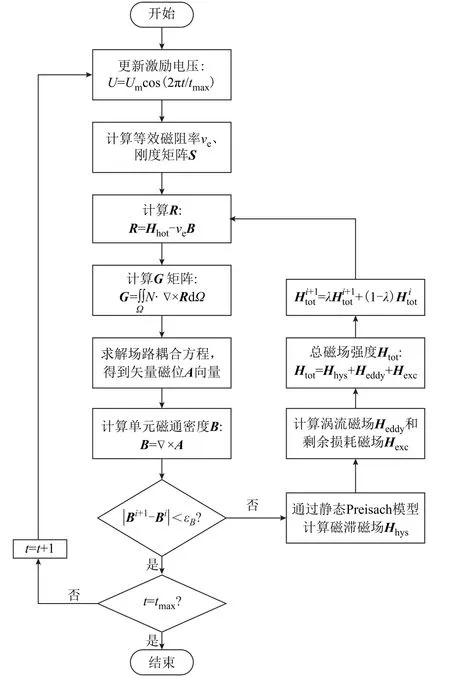
图8 考虑动态磁滞特性的有限元分析流程Fig.8 Finite element iterative calculation process considering dynamic hysteresis characteristics

需要说明的是：不同于静态磁滞磁场，动态磁场强度和磁通密度间的非线性关系不是一开始就确定的，由于涡流磁场和剩余损耗磁场不是直接通过有限元磁场方程表达，而是在固定点迭代过程加入，这意味着在算法迭代过程中，非线性磁场关系不断改变，由动态磁场分量带来的数值扰动使得磁矢位A和磁通密度B计算结果变化剧烈，造成收敛困难，尤其在磁通密度的零点附近，dB/dHtot较大，磁场强度的计算误差引起的数值振荡更大。因此松弛因子λ的引入是十分必要的。

4 结果与讨论

4.1 爱泼斯坦方圈动态磁滞回线有限元模拟

为说明本文所提方法的有效性，在计算模型中，选取了爱泼斯坦方圈臂上的三角形单元作为磁滞回线与损耗的观测点，其二维网格剖分情况如图9 所示，三角网格M 为进行实验数据与模型计算数据的对比的参考单元。在50 Hz 正弦条件下，图10a、图11a 分别给出了激励电压幅值为Umax=9 V 和Umax=13 V 时M 单元处磁滞回线测量值与计算值的对比。可以看出，再考虑动态磁滞特性后，本文所提方法具有较高的磁滞回线模拟精度。进一步地，图10b、图11b 给出了相应电压激励条件下爱泼斯坦方圈励磁电流波形的模拟结果。由于考虑了动态磁场与磁滞效应对电流波形的反馈作用，本文所提方法可以较好地模拟励磁电流时域波形。

图9 爱泼斯坦方圈有限元剖分Fig.9 Finite element mesh of Epstein frame

图10 Umax=9 V 电压激励下测量值与计算值对比Fig.10 Comparison between measured and calculated values under voltage excitation Umax=9 V

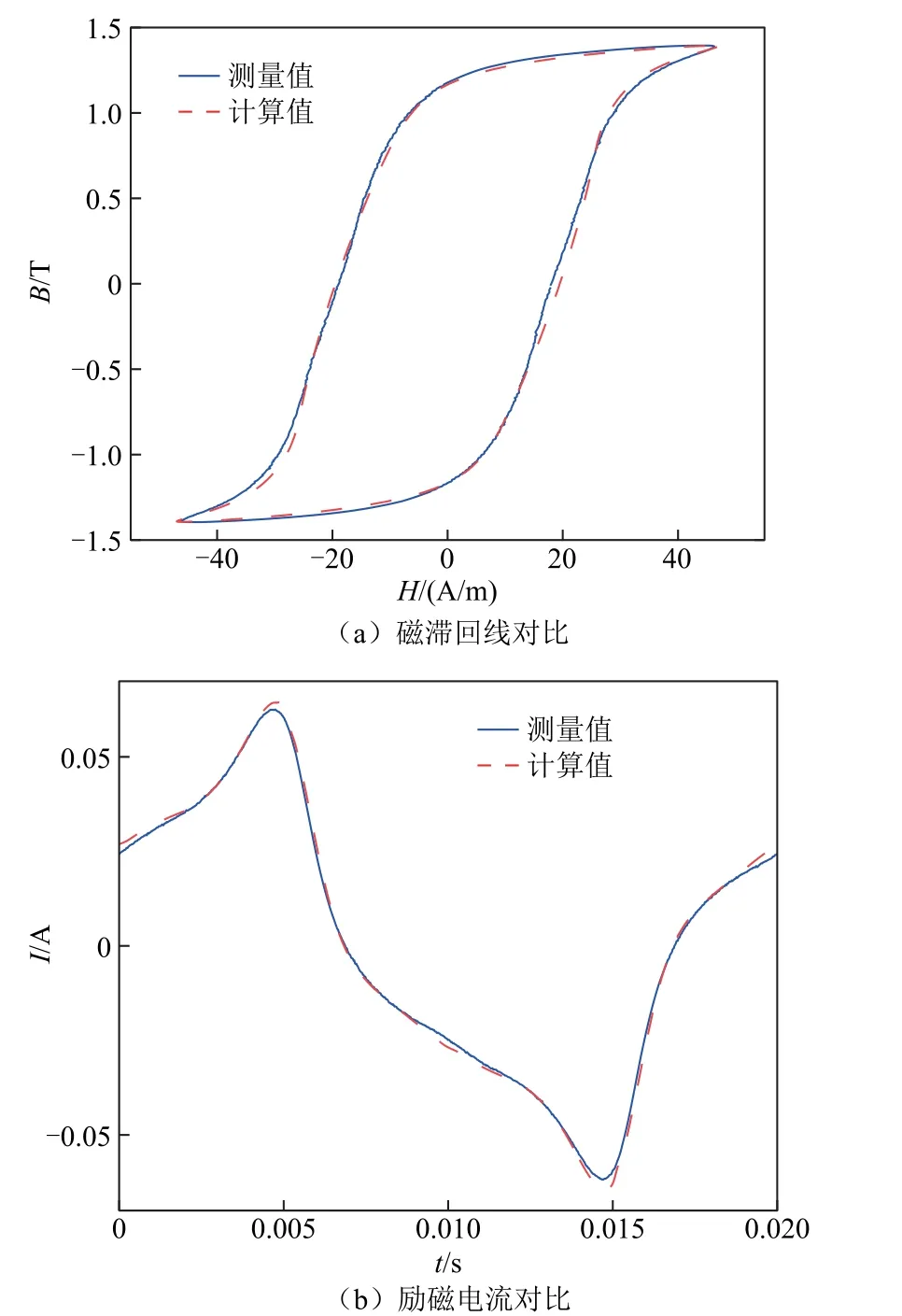
图11 Umax=13 V 电压激励下测量值与计算值对比Fig.11 Comparison between measured and calculated values under voltage excitation Umax=13 V

为考察松弛因子λ对程序收敛性的影响，控制电压激励分别为Umax=9 V，调节松弛因子大小，记录程序是否收敛，以及程序收敛情况下一周期内的平均迭代次数和程序总计算时间。结果见表3，当λ=0.8时，有限元迭代过程不收敛，在确保收敛的情况下，采用较大的松弛因子可减少每时步的平均迭代次数和总计算时间，提升计算效率，最短总计算时间为228 s。通常，为同时满足稳定性和计算速度的要求，设置λ=0.5～0.7 即可。

表3 9 V 电压激励时不同松弛因子对迭代次数和总迭代时间影响Tab.3 Effects of different relaxations on the iterations and computation time with voltage excitation amplitude of 9 V

4.2 磁通密度分布与瞬时损耗特性

为进一步检验算法的有效性，本文对爱泼斯坦方圈的磁通密度分布特性与瞬时功率损耗特性进行了分析与计算。在t=0.005 s 时的磁通密度分布计算结果如图12 所示。可以看出，主磁路上磁通密度分布较为均匀，侧壁上磁通密度幅值计算结果与实验测量值基本一致；而在叠片的内角处，磁通密度较大，在外角部分磁通密度较小。

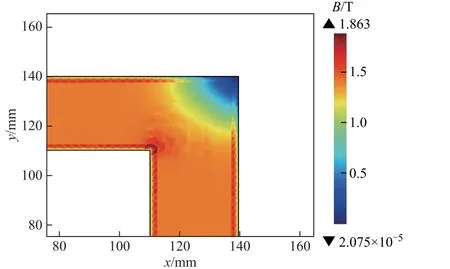
图12 磁通密度分布（Umax=13 V、t=0.005 s）Fig.12 Distribution of magnetic flux density (Umax=13 V、t=0.005 s)

根据4.1 节中磁通密度B和动态磁场Htot计算结果，本文进一步计算了Umax=9 V 和Umax=13 V 两种激励大小在参考单元M 处一周期内的瞬时损耗功率tp并与测量值进行对比，结果如图13 所示。在t=0.00 2 s 和t=0.012 s 附近，测量与计算的瞬时损耗达到极大值；在t=0.005 s 和t=0.015 s 附近，瞬时损耗达到极小值。损耗负值来源于可逆磁化的贡献。可以看出，本文所提方法在模拟瞬时功率方面具有较高的精度，瞬时损耗的最大误差不超过6%。

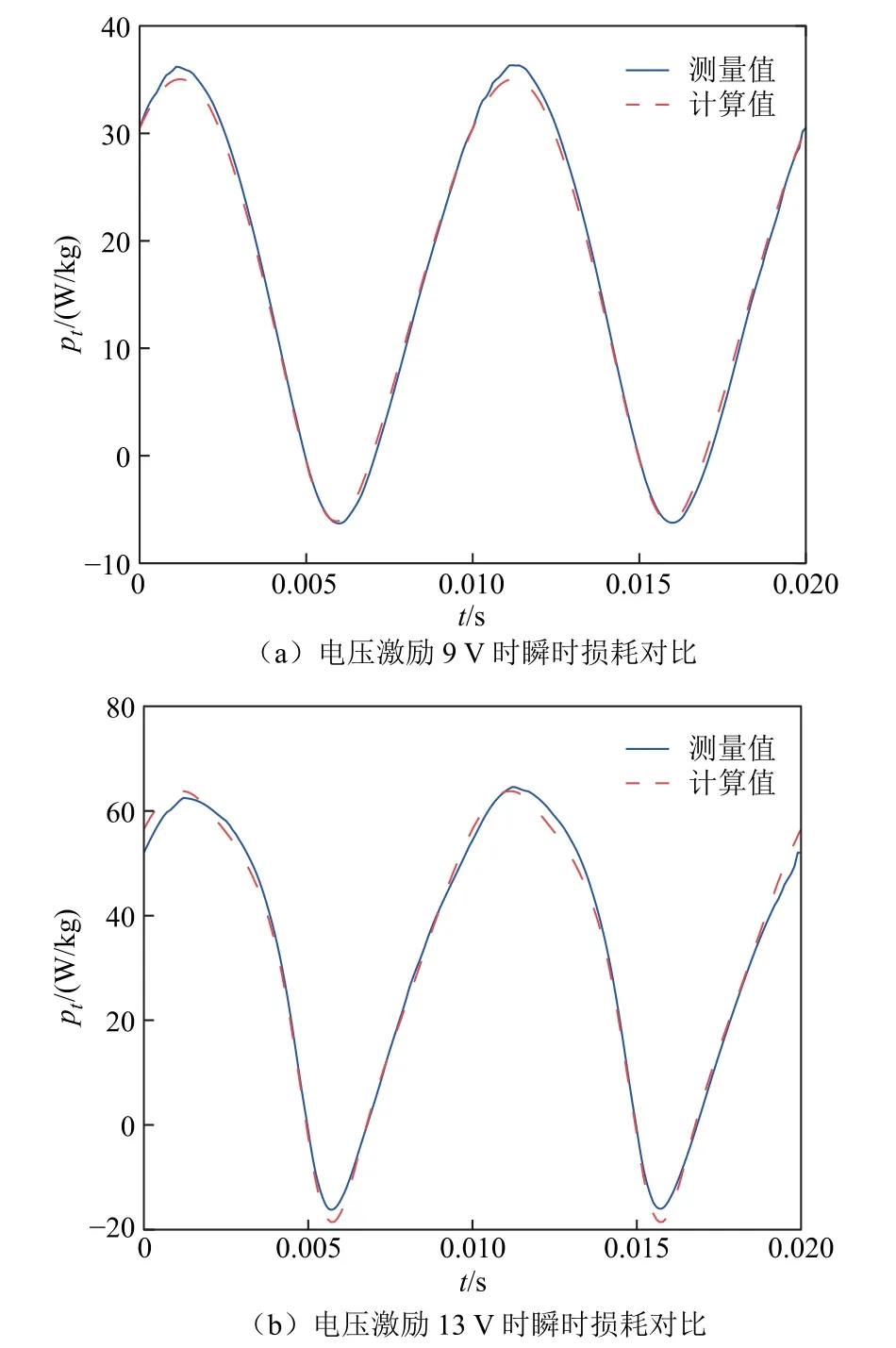
图13 动态磁滞瞬时损耗测量值与计算值对比Fig.13 Comparison between measured and calculated instantaneous loss when considering dynamic hysteresis

完成一个周期有限元计算后，积分得到每一个单元磁滞回线的面积并求和即可得到铁心区域整体铁心总损耗PFe为

式中，f为激励的频率；ne为铁心离散单元总数。图14 所示为不同磁通密度幅值时的铁心总损耗计算值和测量值大小。可以看出，通过提出的有限元算法计算得到的一个周期内的铁心损耗与实验测量结果基本一致。

图14 铁心损耗测量值与计算值对比Fig.14 Comparison between measured and calculated power losses

5 结论

为解决时域有限元分析中考虑铁心材料的动态磁滞特性出现难以收敛的问题，本文提出了一种基于等效磁阻率的高效稳定改进固定点迭代策略，并编写了相应的有限元程序，实现了硅钢片的动态磁滞特性进行模拟计算，并通过实验测量结果对比，验证了该有限元算法的有效性与准确性，具体贡献如下：

1）采用解析方法生成一阶回转曲线，辨识逆Everett 函数，建立逆Preisach 磁滞模型，可准确模拟电工钢片静态磁滞特性。

2）采用固定点迭代技术耦合动态磁滞特性，通过分析涡流损耗和剩余损耗等效磁场对有限元迭代过程的影响，提出基于等效磁阻率的固定点策略，并在有限元迭代过程引入松弛因子，通过实验数据与计算结果的对比分析，验证了本文提出的方法可实现低频动态磁滞磁场的准确计算，并具有良好的计算速度和稳定性。

3）通过场-路耦合有限元算法与动态磁滞模型结合，可充分考虑铁心总损耗对电路和磁场的反馈效应，实现瞬时损耗的准确计算，最大计算误差不超过6%，可满足工程计算要求。