含绝对值不等式问题的处理策略初探

李 鼎

(甘肃省酒泉市瓜州县第一中学)

绝对值不等式是«不等式选讲»中的重要内容,与其有关的考题主要涉及解含绝对值的不等式、含绝对值的不等式恒成立、能成立问题以及绝对值不等式的证明等.解题的关键是“去绝对值”.常用的策略主要有利用绝对值的几何意义、零点分段讨论法、数形结合法、绝对值三角不等式等,下面就这些策略的应用举例分析.

1 利用绝对值的几何意义

|a－b|表示数轴上的点a与点b之间的距离,|a＋b|表示数轴上的点a与点－b之间的距离,这就是绝对值的几何意义.同理,|a|可视为数轴上的点a到原点的距离.

例1 不等式|x－1|＋|x＋2|≥5 的解集为_____.

|x－1|表示数轴上的点x到点1 的距离,|x＋2|表示数轴上的点x到点－2的距离.求不等式|x－1|＋|x＋2|≥5的解集,即在数轴上寻找到点1,－2的距离之和大于或等于5的点的集合.

在如图1所示的数轴上标出点1,－2的位置,易知这两个点之间的距离是3,我们先找出到这两个点的距离之和等于5的点,即－3和2.因此,不等式|x－1|＋|x＋2|≥5的解集为(－∞,－3]∪[2,＋∞).

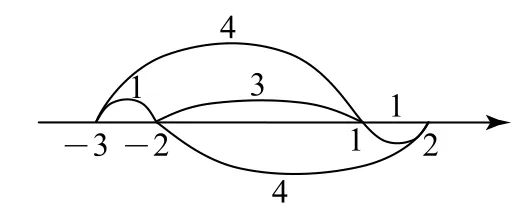
图1

变式 不等式|2x－1|＋|2x＋1|≤6 的解集为_____.

2 利用零点分段讨论法

在处理含绝对值的不等式时,先求出每个绝对值均为零时变量的值,即零点,根据零点将变量的取值范围分成多个区间,在每个区间内讨论各绝对值的正负情况,去掉绝对值.

例2 不等式|3x＋1|－2|x－1|≥1 的解集为______.

3 利用数形结合法

与绝对值有关的不等式问题,往往可以通过构造函数,利用函数图像之间的位置关系来判断满足不等式成立的条件.

例3 若关于实数x的不等式|x－1|＋|x－3|≤a2－2a－1的解集为空集,则实数a的取值范围是_________.

设函数f(x)＝|x－1|＋|x－3|,不等式|x－1|＋|x－3|≤a2－2a－1 的解集为空集,即函数f(x)的最小值大于a2－2a－1.

画出函数f(x)的图像,如图3所示,其最小值为2,所以a2－2a－1＜2,解得－1＜a＜3,即实数a的取值范围是(－1,3).

图3

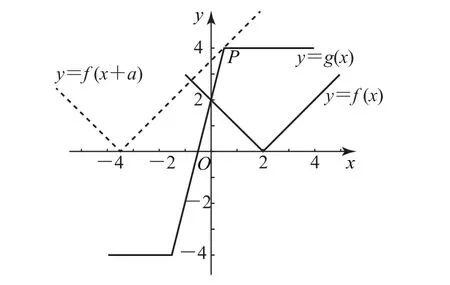
图4

变式 已知f(x)＝|x－2|,g(x)＝|2x＋3|－|2x－1|.若f(x＋a)≥g(x)恒成立,则实数a的取值范围是________.

4 利用绝对值三角不等式

绝对值三角不等式:|a|＋|b|≥|a＋b|,其中a,b为实数,等号成立的条件是ab≥0.同理,|a|＋|b|≥|a－b|,等号成立的条件是ab≤0.

例4 设函数f(x)＝|x＋4|,若f(2x＋a)＋f(2x－a)≥4恒成立,则实数a的值为_________.

由已知得f(2x＋a)＋f(2x－a)＝|2x＋a＋4|＋|2x－a＋4|,利用绝对值三角不等式得|2x＋a＋4|＋|2x－a＋4|≥|(2x＋a＋4)－(2x－a＋4)|＝|2a|,故|2a|＝4,解得a＝±2.

针对某类含绝对值不等式的问题,有些方法可以通用,但有些方法简捷,有些方法烦琐,同学们只有针对题目条件择优而用,才能快速、准确解题.

(本文系甘肃省酒泉市教育科学“十四五”规划2022年酒泉市教育科研课题“基于高中数学核心素养下直观想象能力的培养”的研究成果(课题编号:JQ[2022]GHB228).)

(完)