医疗器械临床试验单组目标值法样本量计算不同方法的比较

曾治宇

波科国际医疗贸易（上海）有限公司

李青

波科国际医疗贸易（上海）有限公司

张晓星

波科国际医疗贸易（上海）有限公司

彭琳

波科国际医疗贸易（上海）有限公司

曾理

波科国际医疗贸易（上海）有限公司

张豫伟

波科国际医疗贸易（上海）有限公司

韩磊

波科国际医疗贸易（上海）有限公司

近年来，单组目标值法的临床研究设计日益受到关注，特别是在医疗器械的临床试验领域[1]。计量资料的单组目标值法的样本量计算方法较为一致，而对于计数资料，样本量计算的方法仍有不同的考虑。

二分类计数资料的单组目标值法的本质是单样本率与已知总体率的比较，即事先确定一个目标值π0（总体率），设定显著性水平α（通常为单侧检验，取值0.025）和检验效能1-β（β通常取值0.2 或0.1），然后将本研究组预计达到的结果π1（样本率）与之比较，从而获得样本量。假设检验时，如果是高优指标（如治疗成功率），当π1的1-2α可信区间的下限不小于π0时则拒绝无效假设，接受π1≥π0，低优指标（如并发症发生率）同理。

目前单样本率比较的样本量计算通常有6 种方法：

（1）正态近似法A。Chow等[2]推荐的基于正态近似法的样本量计算公式为：

其中，π0和π1分别为总体率（目标值）和样本率（期望值），Zα和Zβ分别为α和β所对应的标准正态分布的分位数。

（2）正态近似法B。《医学统计学》（第4 版）[3]中推荐使用的计算公式为：

（3）通用法。《医学统计学》（第3 版）[4]、中国临床试验生物统计学组发表的《单组目标值临床试验的统计学考虑》[5]及2018年原国家食品药品监督管理总局发布的《医疗器械临床试验设计指导原则》[6]等推荐使用的计算公式为：

（4）反正弦法。当π0或π1接近0 或1 时正态性较差，宜考虑数据转换，根据平方根反正弦转换的样本量计算公式为[4]：

（5）确切标准法。使用基于二项分布理论的确切概率法计算样本量[7]。由于单样本率确切概率法获得的样本量与检验效能非单调递增[8-9]，会产生一个常规的结果和一个较为保守的结果，前者即为确切标准法。

（6）确切保守法。方法（5）中产生一个较为保守结果的方法即为确切保守法。

这6 种样本量计算的方法孰优孰劣，具体的适用条件如何，尚无系统的研究。本研究旨在利用计算机模拟分析，考察不同方法计算的样本量及其相应的最低成功率、检验效能，探索不同方法的使用条件，为实际应用中方法的选择提供依据。

1 方法

1.1 构建π0 和π1

构建π0从0.01 至0.99，按0.01递增。π1比π0分别增加0.01，0.05 及0.1。低优指标可根据率的对称性转化为高优指标，比如某研究的并发症发生率目标值为10%，预计研究组的并发症发生率可降至5%，可将低优指标（并发症发生率）转化为高优指标（治疗成功率），即治疗成功率的目标值为90%，预计研究组可提高至95%。为方便起见，本研究仅考察高优指标。

1.2 不同样本量计算方法的评价

本研究的评价指标包括样本量、最低成功率和检验效能。一般来说，在满足α及β的情况下，样本量越小越好；检验效能则越高越好；而对于最低成功率，该值越高提示对产品应用效果的要求越高，该值越低则在研究或生产质控环节更易达到假设检验的显著性，获得阳性结果。

1.2.1 样本量计算

基于构建的π0和π1，设定α=0.025（单侧），β=0.2。根据正态近似法A、正态近似法B、通用法、反正弦法、确切标准法及确切保守法6 种方法的计算公式，分别计算各自所需的样本量。

1.2.2 最低成功率

不失一般性，选择π1=π0+0.1的情形，根据计算出的样本量，编程计算求得所需的最小成功例数，即可获得实际的成功率。所需的最小成功例数为满足该成功率95%可信区间下限≥π0所需的最小例数。95%可信区间的构建需与样本量计算的方法一致，即正态近似法及通用法采用正态近似的方法构建，反正弦法采用平方根反正弦转换后再进行正态近似的方法构建，而确切标准法和确切保守法根据二项分布的理论构建（Clopper-Pearson 可信区间）。

1.2.3 检验效能

不失一般性，选择π1=π0+0.1的情形，采用计算机模拟计算的方法获得检验效能。根据已知样本量及预计成功率π1，进行二项分布概率抽样获得成功例数，重复10 000 次，统计成功例数≥所需最小成功例数的次数，除以重复次数计算所得即为检验效能。

1.3 统计学分析

本研究的编程及统计分析均使用R语言 v3.6.2 和Rstudio平台 v1.2.5033，使用的R 语言包有proportion、pwr、TrialSize 及gsDesign。

1.4 实例分析

实例1：《人工耳蜗植入系统临床试验指导原则》[10]中，根据临床经验，开机12 个月后，产品的总体有效率需至少达到70%方可被临床接受（即目标值为70%）。假设被试验产品的总体有效率可以达到85%，计算在双侧显著性水平0.05、把握度80%的情况下的样本量。

实例2：刘江美等[8]的研究中，已知总体率π0=0.07，预期的总体率π1=0.03，设定α=0.05（双侧），检验效能80%，计算样本量。该例子可验证低优指标的情况。

实 例3：设 定π0=0.1，π1=0.2，可验证一下π0＜0.5的情形。

实例4：一项全皮下植入型心律转复除颤器（subcutaneous implantable cardioverter defibrillator，S-ICD）上市后研究[11-12]中，目标值无不适当电击率为91.6%（相当于不适当电击率为8.4%），S-ICD 预计可达到94.6%，α=0.05（单侧），检验效能90%，计算样本量。

考虑到临床研究中可能由于多种因素导致最终入选样本量与计算样本量存在差异，因此对于实例1和实例3，除了计算样本量，还考察实际入选例数在计算样本量±5范围内的最低成功率与检验效能。

2 结果

2.1 样本量

不同方法计算的样本量比较见图 1。由图1 可知，相关规律并不十分明确，但大体趋势为：①在π0＜0.5 时，正态近似法B 的样本量最小，反正弦法次之，通用法与确切概率法较大且相互接近，正态近似法A 的样本量最大。②在π0＞0.5 时，正态近似法A 的样本量最小，其次为通用法、反正弦法与确切概率法且三者较为接近，而正态近似法B 的样本量随着π0的增加而逐渐超过确切保守法的样本量。

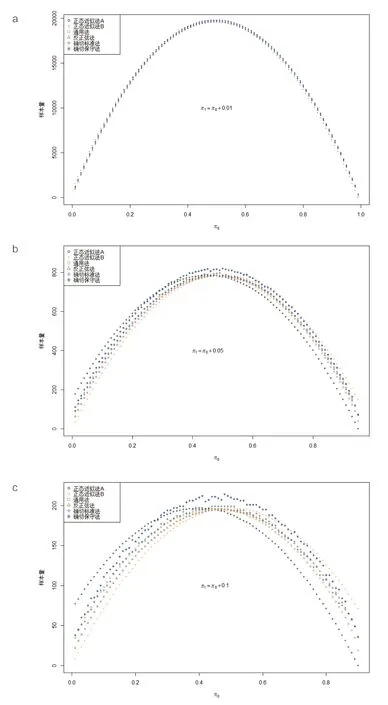
图1 不同方法计算的样本量比较

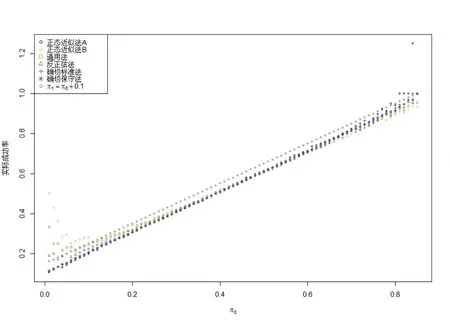
图2 不同方法的最低成功率比较

2.2 最低成功率

不同样本量计算方法下的最低成功率比较见图 2，可见只要π0不是太小，不同方法所需的最低成功率相差不大，且均略小于π1。

2.3 检验效能

不同样本量计算方法下的检验效能比较见图 3。由图3 可知，不同方法的检验效能差异较大。正态近似法B 和通用法在π0＜0.5时检验效能不足，而在π0＞0.5 时检验效能过度，且在π0趋向极端时，这种趋势急剧增加；正态近似法A 的表现与之相反。反正弦法的检验效能基本在0.8 附近，但较确切标准法显得更为离散，特别是π0趋向1 时。确切保守法几乎能确保检验效能在0.8 以上，但在π0＞0.8 时，也表现为检验效能明显增加的趋势。

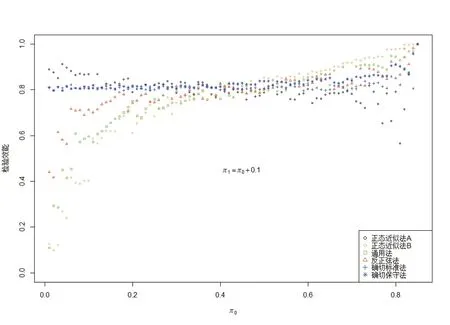
图3 不同方法的检验效能比较

2.4 实例分析

不同方法计算的4 个实例的样本量见表 1，提示不同方法的样本量有一定的差异，但实例1、2、4 的样本量均与原文献[8,10-11]相对应方法的结果相同（原文献采用的方法分别为：实例1 为通用法，实例2 给出了确切标准法和确切保守法的结果，实例4 为确切保守法）。对于实例1 和实例3，计算样本量±5 范围内的比较结果见表2，基本符合图 1、图2 和图 3 的趋势，样本量和检验效能的差异较为明显，表现为：在π0＜0.5 时，正态近似法B 和通用法得到样本量相对较小，但损失了检验效能；π0＞0.5 时，正态近似法B 和通用法样本量相对较大，检验效能也比预设值高。不同方法的最低成功率差异不大，但较大的样本量可以凭借略为较小的最低成功率通过检验。另外，虽然最低成功率的差异总体不大，但在不同方法间仍然存在一些微小的差异，比如对于实例1，当样本量为69 时，正态近似法B 只需成功55 例（成功率79.7%）即可拒绝无效假设，而确切保守法需要成功57 例（成功率82.6%）。

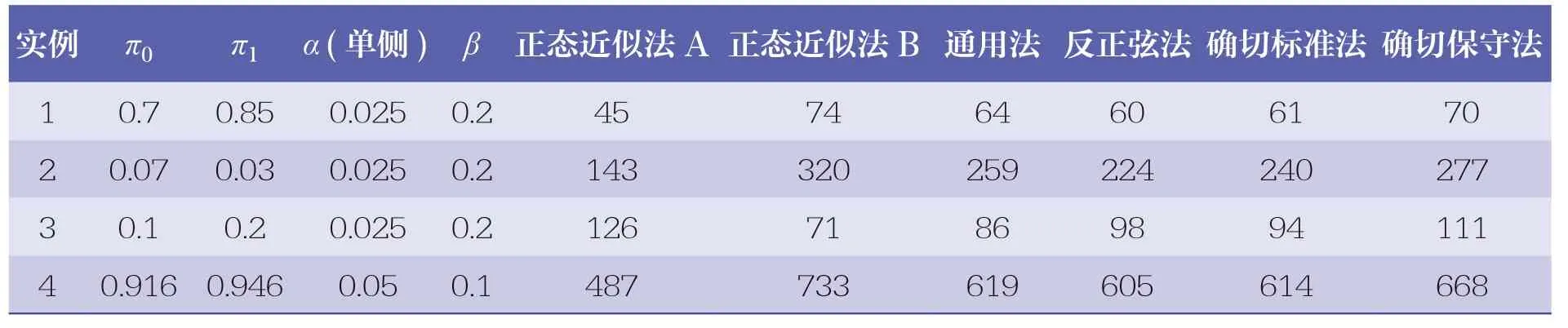
表1 实例分析不同方法计算样本量的结果

表2 不同方法计算样本量的检验效能比较

3 讨论

本研究对单个率比较样本量计算的6 种不同的方法作了较为系统地研究，6 种方法在π0及π1不接近0 或1 时表现较为相似，但π0逐渐接近0 时，正态近似法B 和通用法得到的样本量相对较小，并逐渐损失了检验效能；π0逐渐接近1 时，正态近似法B和通用法的样本量相对较大，检验效能也比预设值逐渐增高。正态近似法B 的表现趋势与A 正好相反。从检验效能来看，反正弦法的结果与确切标准法接近而显得更为离散，而确切保守法几乎能保证预设的检验效能，但在π0＞0.5 时，确切保守法所需样本量逐渐多于确切标准法。不同方法对最低成功率的要求总体相似，但存在微小差别。

目前临床研究中对于这6 种不同方法的选用尚无明确的适用条件。本研究显示通用法的整体表现优于正态近似法，但这些方法本质上都是基于正态近似的原理，当π0趋于极端时，检验效能有较大的变化。《医学统计学》（第3 版）[4]建议当率偏向两侧时（π0＜0.3 或π0＞0.7）使用反正弦法，但本研究中π0在0.4～0.6 范围内时其检验效能才可保持在0.8左右，该结果提示这些方法的临床应用仍具有一定局限性。也有学者[7,13-14]认为nπ及n（1-π）＞5时，可以考虑正态近似法，但是在率较小时，其计算的样本量会相应较大，比较容易满足nπ及n（1-π）＞5 的条件（如实例4），故而这个建议也不理想。

不同方法的比较鲜有研究。有研究[15]比较了通用法和确切标准法，认为π1＞0.85 时，确切标准法所得的样本量及检验效能均低于通用法，且显示通用法检验效能的提高是以样本量增加为代价的，而此时的检验效能已明显大于预设值，这与本研究的结果基本一致。该研究设定的π0从0.7 开始，并未考察π0＜0.5 的情况。本研究中，π0＜0.5 的表现与π0＞0.5 的表现几乎是相反的。值得一提的是，在6 种样本量计算的方法中，除了反正弦法，其他5 种方法中的π0和π1是不可互换的，比如π0=0.1 和π1=0.2 的样本量，与π0=0.2 和π1=0.1 的样本量是不一样的。

本研究的局限性在于：①本研究的模拟基本覆盖了临床常见的一些情形，并且精选了4 个实例做了进一步的分析验证，但主要为计算机模拟分析，未进行深入的理论讨论，并且模拟的情形相对有限。②临床研究中选择样本量的考虑还有其他许多重要因素，比如目标值的确定、对受试者脱落的估计、缺失数据的处理等。本研究无法对众多因素一一考量，在对实例1 和3 的分析中可以看出，根据确切法计算的样本量，实际入选例数不宜轻易减少，否则检验效能达不到预设值。

综上，单个率比较的样本量计算方法的选择较为复杂，从样本量计算本身来看，对检验效能要求比较高时（如产品的上市前研究），宜优选确切标准法和确切保守法，其次可考虑反正弦法，而通用法和正态近似法在率偏向两侧时，样本量会过大或过小，应根据实际应用情况具体权衡。