角钢塔连接螺栓考虑预紧力的拉剪计算方法研究

鄢秀庆,龚 涛,刘翔云,蒲 凡,李 钟

(中国电力工程顾问集团西南电力设计院有限公司,四川 成都 610021)

0 引 言

角钢塔一般采用螺栓连接,螺栓主要承受剪力作用。但GB 50233—2014《110 kV～750 kV架空输电线路施工及验收规范》[1]基于拧紧及防松的目的,要求在施工时施加一定的扭矩,该扭矩将在螺杆内形成一定的拉力,在叠加剪力后使得螺栓处于拉剪受力状态。DL/T 5486—2020《架空输电线路杆塔结构设计技术规程》[2]未要求对螺栓进行拉剪受力的复核,仅给出了纯剪力的计算公式,导致计算结果偏于冒进。

民用钢结构领域的JGJ 82—2011《钢结构高强度螺栓连接技术规程》[3]仅规定了高强度螺栓的紧固扭矩值,对普通螺栓的紧固扭矩值并没有作明确规定;文献[4-7]主要针对高强度螺栓预紧力对其受剪影响进行了系统研究。计算表明,目前规范规定的紧固扭矩值会使得设计偏于不安全,主要是依靠螺栓强度的安全系数进行抵抗。因此,很有必要研究紧固扭矩对普通螺栓受剪的影响。

下面结合钢结构设计原理[8]理论推导了输电塔普通受剪螺栓在预紧力作用下的抗剪剩余承载力比的计算方法,并结合有限元分析对该方法进行了论证。同时采用有限元精细化数值模拟分析了预紧力对普通螺栓抗剪承载力的影响,验证了理论推导结论;最终依据预紧力和抗剪承载力之间的关系,推荐了输电塔普通抗剪螺栓的紧固扭矩值,为工程设计提供了设计依据。

1 紧固扭矩对普通螺栓受剪的影响

1.1 紧固扭矩的取值

GB 50233—2014、DL/T 5486—2020给出了受剪螺栓紧固扭矩的最小值,并注明了M24为8.8级螺栓,如表1所示。

表1 常见规格螺栓的施工紧固扭矩值

国家电网公司企业标准Q/GDW 10115—2022《110 kV～1000 kV架空输电线路施工及验收规范》[8]第9.1.7条给出了4.8级、6.8级角钢塔螺栓的最小紧固扭矩,如表2所示。

表2 常见规格螺栓的施工紧固扭矩值

特高压钢管杆塔法兰螺栓的最小紧固扭矩,如表3所示。

表3 特高压工程推荐的施工紧固扭矩值

表1至表3表明,对于6.8级M16螺栓,工程中规定的紧固扭矩值为80 N·m;对于6.8级M20螺栓,工程中规定的紧固扭矩值为100～160 N·m;对于8.8级M24螺栓,工程中规定的紧固扭矩值为250～380 N·m。

1.2 施工预紧力的计算方法

依据《机械设计手册》[9],普通螺栓预紧力P的计算方法为

(1)

式中:K为拧紧力矩系数,计算表明可近似取0.2;d为螺栓公称直径,mm;T为紧固扭矩。

根据各规范紧固扭矩取值,反算预紧力如表4所示。

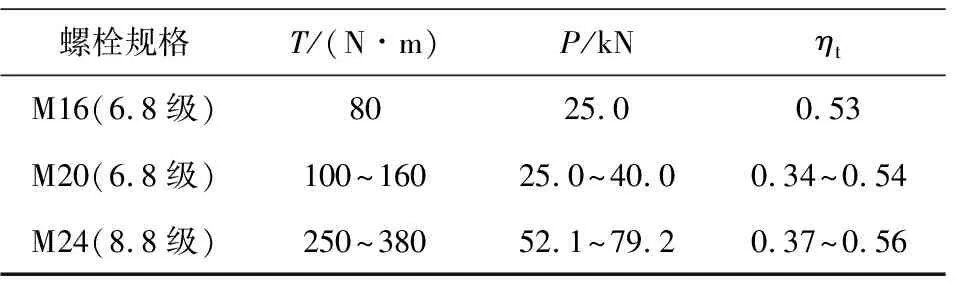
表4 紧固扭矩的预紧力计算值

假定预紧力在输电塔普通螺栓的服役过程中一直存在,此时螺栓会承受拉剪耦合效应,这一定程度削弱了螺栓的抗剪作用,根据GB 50014—2017《钢结构设计标准》[10]第11.4.1条规定,承受拉剪耦合作用时,普通螺栓的承载力应满足式(2)要求。

(2)

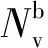
由式(2)可以推导出抗剪螺栓考虑预紧力后的剩余承载力比为

(3)

根据式(3)计算得到考虑预紧力后的抗剪剩余承载力比如表5所示。

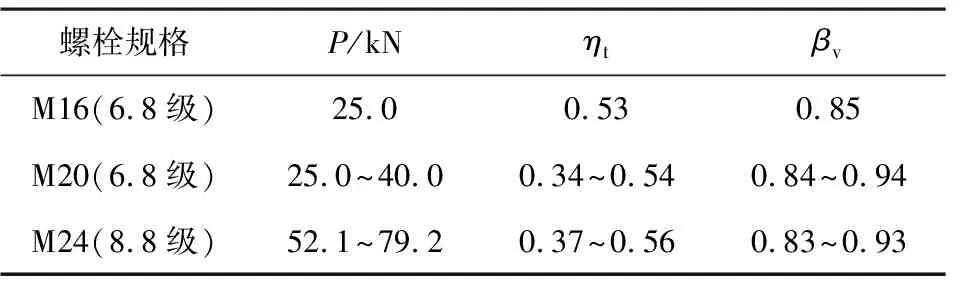
表5 考虑预紧力后的抗剪剩余承载力比

表5表明,由于预紧力的影响,受剪螺栓的抗剪剩余承载力比在0.83～0.94区间,承载力较纯剪时下降了6%～17%,紧固扭矩越大,其抗剪剩余承载力越小。螺栓在实际受力时,由于连接板面镀锌与螺栓连接面存在摩擦。螺栓抗剪滑移时是一个缓慢运动的过程,可以假定这种由于预紧力产生的摩擦力是一直存在,分担了一部分外部剪力,使得螺栓螺杆实际承载的剪切力减小了。镀锌连接面的摩擦系数μ近似取0.15,结合GB 50014—2017高强度摩擦型螺栓的抗剪承载力计算形式,可以假定预紧力产生的摩擦力为

Vμ=0.9μP

(4)

考虑摩擦力后的抗剪剩余承载力比为

(5)

考虑螺栓摩擦力后抗剪剩余承载力比如表6所示。

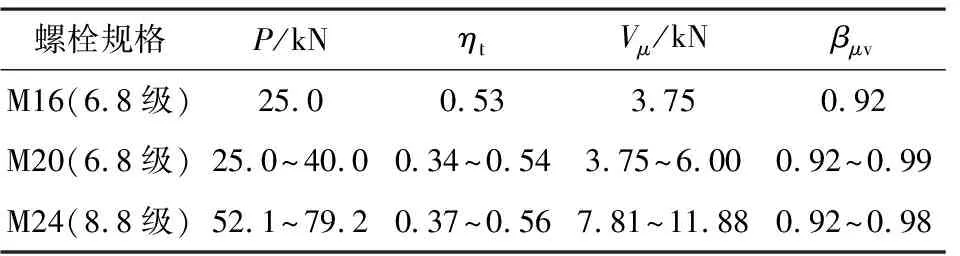
表6 螺栓考虑摩擦力后抗剪剩余承载力比

表6表明,考虑螺栓摩擦力后,剪切螺栓的抗剪剩余承载力比在0.92～0.99区间,仍小于1.0,表明按照规范规定的紧固扭矩进行螺栓紧固后,所产生的预紧力对螺栓的抗剪承载力具有较大削减作用。而这种影响在结构设计中并没有考虑,主要是通过材料的分项系数来抵抗,从设计上来讲,这是偏于不安全的,降低了螺栓的可靠度。

2 数值模型验证

为进一步研究预紧力状态下受剪螺栓的抗剪性能,采用数值模型进行验证。采用板式双剪模型进行数值分析,为了避免螺栓的承压破坏,板件材料强度为Q420,加载板厚度取30 mm,固定板厚度取15 mm,螺栓采用8.8级M24,屈服强度取640 MPa[11],预紧力在螺杆中部截面对称施加,摩擦系数取0.15,模型构造见图1所示。

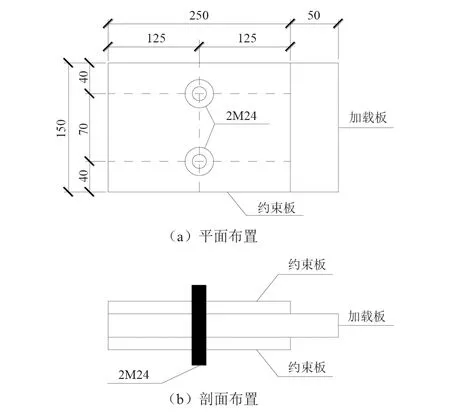
图1 板式双剪模型构造

2.1 数值模型

为了精确模拟螺栓的受力,螺栓与板之间采用接触约束,采用实体单元模拟;材料采用理想弹塑性本构;约束住约束板的左端,在板的右端施加拉伸荷载,进行几何非线性分析。数值模型如图2所示。

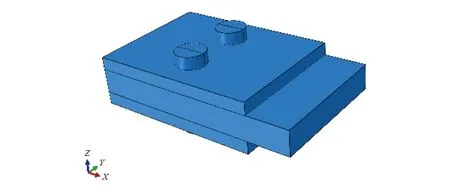
图2 板式双剪模型

按照屈服强度计算出单颗螺栓的全截面塑性抗剪承载力为289.5 kN,由此得到双剪模型的抗剪极限承载力为1158 kN,为了研究预紧力对螺栓抗剪承载力的影响,设计了4种加载工况,如表7所示。

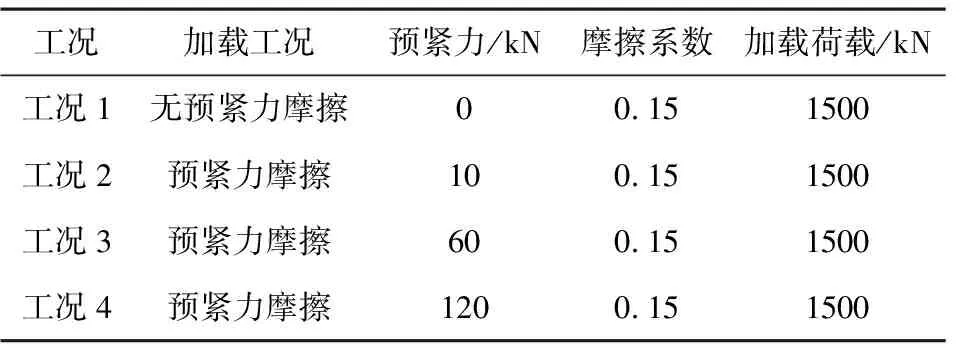
表7 工况信息

2.2 应力云图

在极限破坏状态下,双剪模型的整体应力云图如图3所示。

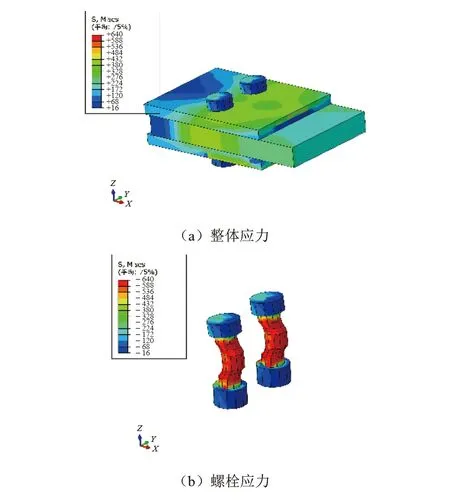
图3 双剪模型的应力云图

图3表明,极限破坏状态下,螺栓附近板的应力已经进入了塑性,螺杆大部分区域也进入了塑性,存在明显的剪切变形,螺栓最终被剪坏。

2.3 预紧力对螺栓抗剪承载力的影响

数值计算得到了所设计的4种加载工况下双剪模型抗剪承载力,如表8所示。

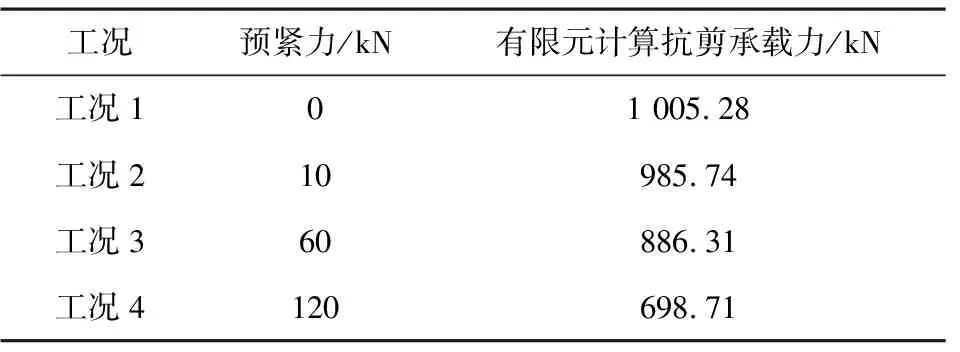
表8 各工况的极限抗剪承载力

由表8可知,预紧力为0时,抗剪承载力为1 005.28 kN;随着预紧力的增加,双剪模型的抗剪承载力逐渐减小,预紧力越大,这种减小趋势越明显,近似呈二次抛物线减小,如图4所示。

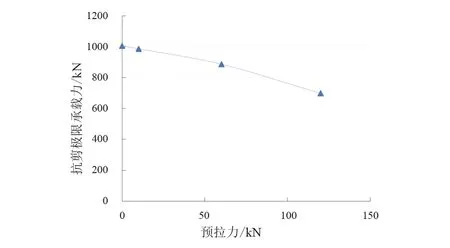
图4 预紧力对螺栓抗剪承载力的影响

数值分析表明,随着预紧力增大,螺栓的抗剪承载力是减小的,这与第1.2节理论分析结论是一致的,且预紧力越大,螺栓抗剪承载力减小越明显。因此,工程设计中需要考虑预紧力对普通螺栓的抗剪承载力影响。

2.4 参数分析论证

为了综合对比理论计算公式的有效性和可靠性,进行参数分析,如表9所示。参数分析的变量包括螺栓型号、预紧力及摩擦系数,共计36组。

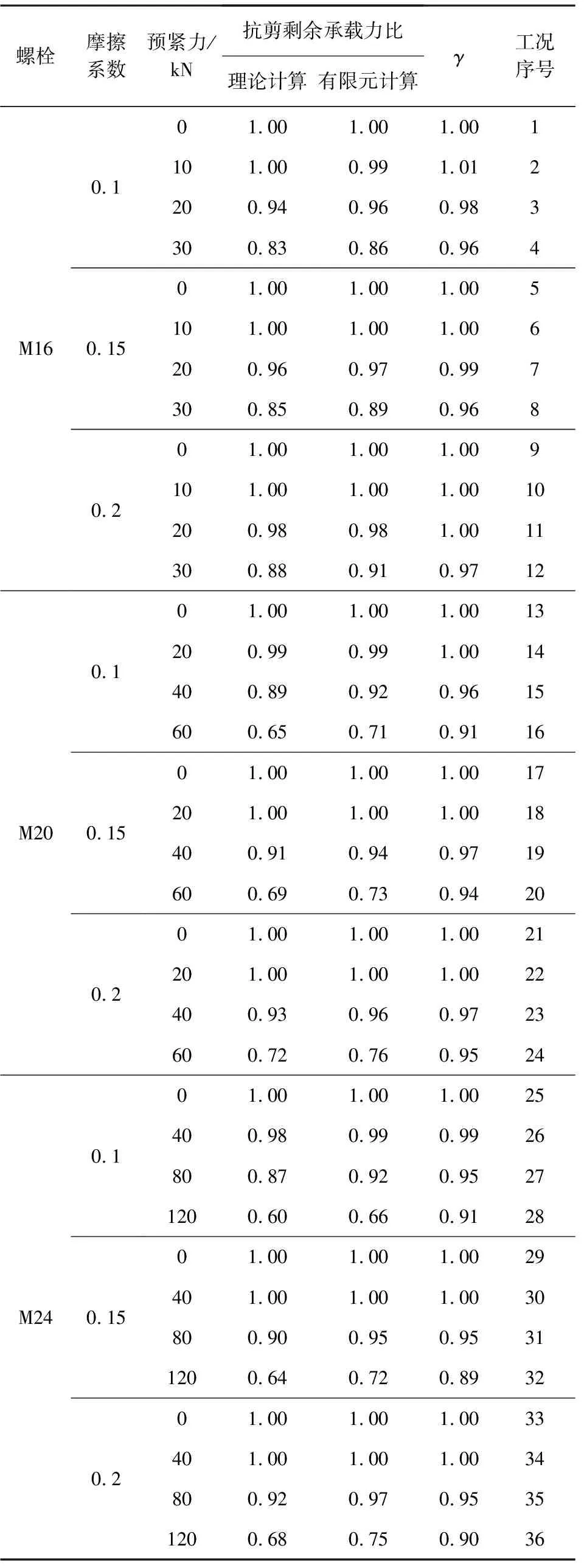
表9 各工况的抗剪剩余承载力比

改变有限元模型的部分参数,进而计算M16、M20及M24螺栓在各工况下的抗剪剩余承载力比,并定义γ为理论计算与有限元计算抗剪剩余承载力比的比值,作出各工况下的γ如图5所示。可以看出:理论计算抗剪剩余承载力比略大于有限元计算抗剪剩余承载力比,且保证率约为97%,整体吻合良好。

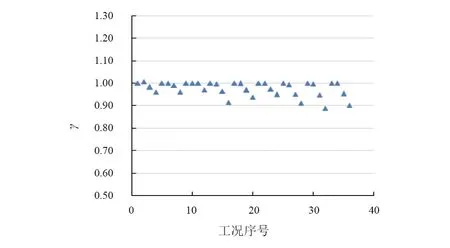
图5 各工况的理论计算与有限元计算抗剪剩余承载力比的比值

3 普通螺栓紧固扭矩取值推荐

理论推导和数值研究结论表明,预紧力对普通螺栓抗剪承载力存在一定的影响,预紧力越大,其抗剪承载力削弱越明显。目前输电塔普通螺栓在抗剪设计时,并没有考虑紧固扭矩所产生的预紧力影响。计算表明,按照现有标准规定的紧固扭矩进行螺栓拧紧,其产生的预紧力对设计来说是偏于不安全的,因此有必要重新推荐普通螺栓的紧固扭矩值,保证设计的可靠性。

按照式(5)计算6.8级M16、6.8级M20和8.8级M24螺栓在不同预紧力下的螺栓抗剪剩余承载力比,如图6所示。

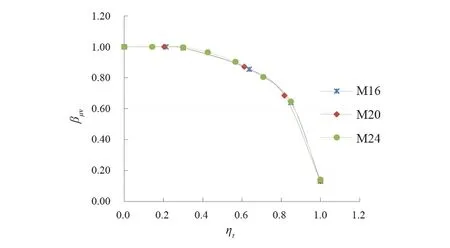
图6 预紧力对螺栓抗剪剩余承载力比的影响

图6表明,预紧力越大,螺栓抗剪剩余承载力比越低,近似呈二次抛物线关系。ηt不大于0.3时,可不考虑预紧力对螺栓受剪力的影响。同时,文献[3]中关于承压型螺栓,将其分为适度拧紧型和完全预紧型,适度拧紧型为采用扳手拧紧达到连接面紧密结合的目的,主要用于受拉或拉剪组合螺栓,与输电塔受剪普通螺栓受力一致。因此,对于输电塔受剪普通螺栓,建议结合文献[3]的规定,以观察为主,同时施加扭矩时的预紧力不超过设计抗拉承载力的30%。推荐施工紧固扭矩如表10所示,施工过程中紧固扭矩值应不大于表10中的值。

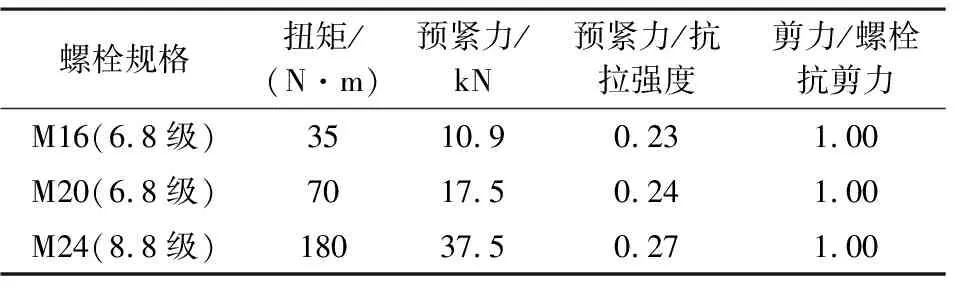
表10 输电塔普通螺栓紧固扭矩推荐值

4 结 论

上面结合钢结构基本原理推导了输电塔普通受剪螺栓在预紧力作用下的抗剪剩余承载力比计算方法,并结合有限元分析对该方法进行了论证;结合精细化数值模拟论证了预紧力对普通螺栓抗剪承载力的影响,验证了理论分析的结果;最终依据预紧力和抗剪承载力之间的关系,推荐了输电塔普通抗剪螺栓的紧固扭矩值,为工程设计提供了设计依据,具有一定的工程价值。主要研究结论如下:

1)总结了目前各标准对于普通螺栓紧固扭矩的相关规定。各标准对于M20、M24要求差异较大,产生的预紧力占螺栓抗拉承载力比例较高。分析并提出了预紧力对普通螺栓抗剪承载力的影响。

2)结合钢结构设计原理推导了普通螺栓在预紧力作用下的抗剪剩余承载力比计算方法。结果表明,考虑预紧力及板件表面摩擦力后,剪切螺栓的抗剪剩余承载力比在0.92～0.99区间,采用有限元参数分析,论证了这一分析结论。

3)结合精细数值模拟分析论证了预紧力对普通螺栓抗剪承载力的影响。研究表明,预紧力会影响普通螺栓的抗剪承载力,预紧力越大,抗剪承载力减小越明显,近似呈二次抛物线关系。

4)计算表明,ηt不大于0.3时,可不考虑预紧力对螺栓抗剪承载力的影响。

5)基于研究结论和文献[3]关于螺栓的相关紧固要求,推荐了输电塔施工过程中普通螺栓紧固扭矩值。