（2，2）-同源的有效计算

张 婷 李梦东

北京电子科技学院密码科学与技术系，北京市 100070

0 引言

在过去几年里，基于椭圆曲线之间同源映射的密码学因为其可以抵抗量子攻击且密钥长度短的性质而取得了很大的进展，而其代表算法SIDH（Supersingular Isogeny Diffie Hellman）的改进算法SIKE［1］进入到NIST 的第四轮筛选。 但最近Castryck 和Decru 提出了有效破解SIDH 的攻击方法［2］，使得SIKE 不再安全。 其主要攻击点为SIDH 中附加的挠点信息，采用的方法是计算椭圆曲线乘积及粘连后形成的超椭圆曲线Jicobian 之间的（2n，2n）-同源。

超椭圆曲线密码（HECC）是椭圆曲线密码（ECC）的推广，其中考虑了超椭圆曲线的雅可比（Jacobian）上的群运算。 虽然这种雅可比的群计算比椭圆曲线更复杂，但它允许使用比椭圆曲线更小的素数域。 G2SIDH 是将SIDH 方案推广到亏格2 的超椭圆曲线上的密钥协商协议［3］。正如预期的那样，G2SIDH 与SIDH 相比只需要其三分之一的比特长。 虽然这允许更快的素数域算术，但此时计算同源更加复杂。 其中主要计算步骤也是超椭圆曲线的Jacobian、椭圆曲线乘积之间（2n，2n） 同源计算。

（2n，2n）-同源是（2，2）- 同源的n 次迭代，因此（2，2）-同源的快速计算具有重要价值。 一般的计算（2，2）- 同源的方法是Richelot 对应［4］。 Richelot 对应提供了一种计算元素J ∈（为一个Jacobian）的像的方法，包括四个步骤（参见2.1 的算法一），特别是需要计算一个表示J 的除子∑k i＝1Pi∈Div（C） 的支撑度。 这涉及多次平方根计算，还在大约一半的情况需要用到基域的2 阶扩展。 2022 年S.Kunzweile 提出交换曲面之间的特定形式的同源核的（2，2） -同源一个计算公式和相应快速算法［5］，虽然该算法计算（2，2）-同源的方法也依赖于Richelot 对应，但不需要计算平方根，并且只需要在基域中进行标准加法和乘法运算。 该算法可显著提高（2，2）-同源的计算速度。

本文主要在已有算法［5］基础上，对（2，2） -同源计算过程进行了优化和改进，重点对除子的Mumford 表示形式中多项式系数的计算进行改进。通过分析各表达式中各参数的前后关系，预先计算显示公式中的部分信息，以提高显示公式部分计算的速率，从而相比原算法实现进一步提高了整个同源计算的效率。 本文通过实验编程验证了改进算法的正确性，并与原算法的复杂度进行了对比。 改进算法节省了27m＋10s 的计算成本，使用Python编程随机选取参数并取100 组平均值的实现结果中，改进算法相比于原算法节省了12456ns。

1 背景知识

1.1 超椭圆曲线

设Fq是域Fq的代数闭包。 域Fq上亏格为g且g≥2 的超椭圆曲线C 定义如下：

其中f（x） ∈Fq［x］ 是一个次数为2g＋1 的首一多项式，h（x） ∈Fq［x］ 是次数至多为g 的多项式，并且没有解可以同时满足方程y2＋h（x）y＝f（x） 和两个偏导数方程2y＋h（x）＝0 和h′（x）y-f′（x）＝0。 若点（x，y）同时满足两个偏微分方程，那么称其为奇异点，因此，C 是一个非奇异的超椭圆曲线，在无穷远处只有一个点P∞。 对于Fq的任何代数扩张Fqk，考虑集合C(Fqk) ∶＝｛（x，y）∈Fqk×Fqk｜y2＋h（x）y＝f（x）｝∪｛P∞｝，称为C 上的Fqk-有理点的集合。

本文主要讨论亏格为2 且h（x）＝0 的超椭圆曲线，其曲线方程主要有两种形式：

其中A，B，C，E∈Fq。

1.2 除子和Jacobian

超椭圆曲线C 的除子群Divc是在Fq（C）／Fq上的交换群。 一个元素D∈Divc被称为除子，其定义如下：

其中ni∈Z，且只有有限个ni不为零。

除子D 的次数表示为系数的和，即

1.3 Mumford 表示

由一个多项式对＜a（x），b（x）＞可唯一地表示超椭圆曲线C 上Jacobian 中的非单位元素，其中一个有效除子D∈Div（C） 是在一般位置，形式如下：

令D＝P1＋…＋Pd是一个一般位置的除子，a，b∈K［x］ 具有下面性质：

（1）a 是次数为d、首一的多项式；

（2）b 的次数小于d；

（3） f ≡b2mod a；

（4）a（ui）＝0，b（ui）＝vi，其中Pi＝（ui，vi），1 ≤i≤d。

则称（a，b）是D 的Mumford 表示（细节见［5］）。

一般位置的每个除子都满足一个Mumford表示，由于本文研究的是亏格为2 的超椭圆曲线，因 此deg（b） ≤deg（a） ≤2， 每 个 元 素［D］ ∈具有［P1＋P2-D∞］ 形式的唯一表示，其中

为避免歧义，对Mumford（a，b）引入以下符号：

2 已有算法

2.1 Richelot 同源［4］

对于亏格为2 的超椭圆曲线之间的同源，［4］构造一个对应关系，使得（2，2）-同源可依据显式公式进行计算，这也就是一般计算（2，2）-同源的过程。 一般的计算（2，2）-同源的方法又称Richelot-同源的计算。 所谓的Richelot-同源提供了一种在这种同源性下计算元素J∈（是一个Jacobian）的像的方法，该算法包括四个步骤伪代码，见表1。

2.2 Sabrina Kunzweiler 的算法［5］

［5］中提出的算法应用于类型-1 方程的Richelot 同源。

类型-1 方程定义的亏格2 曲线C 如下：

2.2.1 计算C′

令C 是亏格2、由类型-1 方程定义的曲线：y2＝Ex（x2-Ax＋1）（x2-Bx＋），

C′是形如下面的曲线：

算法1：计算（2，2）-同源输入：椭圆曲线C：y2 ＝g1（x）g2（x）g3（x），G ＝＜J（g1，0），J（g2，0） ＞，元素J（a，b） ∈ （C）。输出：椭圆曲线C′，J（a′，b′） ∈ （C′）Step 1 计算C′δ ＝det（（gij）1 ≤i ≤3，0 ≤j ≤2）for i＝1 to 3｛ hi ＝δ-1（g′i＋1gi＋2 - gi＋1g′i＋2）｝C′：y2 ＝h1h2h3 Step 2 计算P，Q ∈C (K- ) ，J（a，b） ＝［P ＋Q - D∞］计算a 的根，即a（u） ＝a（s） ＝0，v ＝b（u），t ＝b（s） 得到P ＝（u，v），Q ＝（s，t）Step 3 计算计算支撑度DP，DQ ∈Div（C′）DP ＝D（aP，bP），DQ ＝D（aQ，bQ）aP ＝monic（g1（u）h1（x） ＋g2（u）h2（x））bP ＝g1（u）h1（u）（u - x）·v-1（modaP）aQ ＝monic（g1（s）h1（x） ＋g2（s）h2（x））bQ ＝g1（s）h1（s）h1（s - x）·t-1（modaQ）Step 4 使用cantor 算法计算［D′］ ＝［DP ＋DQ - 2D∞］a：组合D（a′，b′） ＝Dp ＋DQ ∈Div（C′）b：约束［D′］ ＝J（a″，b″） ∈images/BZ_62_1602_1521_1636_1564.png（C′）

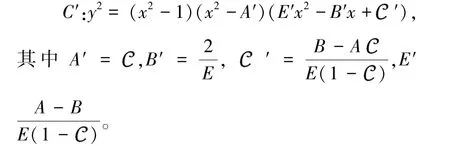
点（P，P′）＝ （（u，v），（u′，v′））∈R⊂C×C′。2.2.3 计算P，Q

计算a的根，得到u，s，考虑到：a（u）＝a（s）＝0，v＝b（u），t＝b（s），得到P＝（u，v），Q＝（s，t），可以看到，只要考虑这个域的扩展就足够了

那么u＝u，s＝-a1-u，v＝b0＋ub1，t＝b0＋sb1。

2.2.4 计算支撑度

对Richelot 对应关系中的第一个方程进行归一化，得到aP。 然后将Richelot 对应中第二个等式的右侧除以v 并模aP来获得bP。

aQ，bQ是通过将（u，v） 替换为（s，t），具体结果见［5］。

2.2.5 显式公式

算法一［4］中的前三步对应到［5］分别是2.2.1，2.2.3，2.2.4，对于第四步，［5］提出了Richelot 同源ϕ的显示公式，这一公式可理解为计算任意元素J（a，b） ∈（C） 的像ϕ（J（a，b））。 该显示公式有如下三个条件：

（1） 0 ≠a0B2＋（a0＋1）a1B＋（a0- 1）2＋a21等价于要求u2- Bu ＋1 和s2- Bs ＋1 不零。

（2） 0 ≠-b1（a1b0-a0b1）＋b20 意味着P 和Q 都不是Weierstrass 点，因此v，t≠0。

（3） 0 ≠（a0- 1）（a21- 4a0）， 意 味 着gcd（aP，aQ）＝1，此时a′＝aP·aQ。

执行Cantor 算法的合成步骤，输出Mumford表示D（a′，b′）＝DP＋DQ时，我们的目标是消除元素u∈L＼K以获得在K 上定义的公式。 利用条件3，使a′＝aP·aQ，由于aP和aQ表达式的对称性，可以发现a′ ∈K［x］L［x］。 ［5］中定理4.7 提供了a′ 系数的公式。 对于b′ 的计算，有限制条件：b′（ui）＝vi，b′（si）＝ti，i∈｛1，2｝ 这是由下述多项式来满足的

对于计算，有必要进一步扩展定义域到M＝L［u1，s1］／（aP（u1），aQ（s1）） 使得：

计算b′的表达式同时考虑不同变量之间的关系，从［5］中定理4.7 得到了b′ ∈K［x］的公式。 从而得到D（a′，b′）。

通过计算得到如下显示公式：

其 中 对 于a′，b′ 的 系 数 的 具 体 公 式请见［5］。

上述显示公式取代算法一的步骤1，2，3，4（a）。 这导致同源计算的一个主要提速，因为所有平方根计算、域扩展都可避免。 为发现除子类（C） 的Mumford 表示（a″，b″）， 只剩下步骤4（b）。 这包括两个计算：

（1）计算商（f-b′2）／a′， 其中f＝（x2-1）（x2-A′）（E′x2-B′x＋C′） 是C′的定义多项式，这个商的正规化是次数最多2 的首一多项式（即把最高次项系数变成1）。

（2）计算剩余-b′moda″， 这个剩余是多项式b″，其次数小于a″。

经过第一步的计算可以得到a″， 第二步的计算可以得到b″， 由此得到了ϕ（J（a，b））＝［D′］＝J（a″，b″）。

3 改进的实现算法

由于Jacobian 群运算的复杂性，使得同源的运算需要大量时间。 S.Kunzweile 算法［5］主要是将对类型二的超椭圆曲线的同源算法进行改进，将类型二的亏格为2 的超椭圆曲线转为类型一，进而对求根过程进行扩域中计算，但是最后其执行Cantor 算法步骤时消除了扩域元素，得到的结果依旧在基域中，经过计算之后得到ϕ（J（a，b）） 的显示公式。 而本文在S.Kunzweile 等学者的工作基础上对其（2，2）-同源计算公式进行了进一步优化，而原公式是未经优化的。 预先存储显示公式中的部分信息，可提高显示公式部分计算的效率。

上述显示公式中：

经观察，上述系数的显示公式中出现多个相同项 即（a0- 1）2＋a21，（a0＋1）a1，因此可进行预先计算该相同项，减少公式的计算成本。 伪代码如表2 所示。

4 性能分析

一般情况下，我们用m，s 表示有限域中的乘法运算和平方运算，用ns 表示纳秒。 根据显示公式可知未改进之前对于a′多项式系数的计算成本是29m ＋11s，对于b′多项式系数的计算首先有2m 的预计算（即μ） 成本以及67m＋8s的公式计算成本，因此改进之前的显示公式的总计算成本为98m＋19s。 各参数计算成本如下：

算法2：改进的显示公式输入：a0，a1，b0，b1，A，B，C输出：a′4，a′3，a′2，a′1，a′0，b′3，b′2，b′1，b′0，b′den Step 1 预计算M，N，μ（a0 - 1）2 ＋a21 ＝M（a0 ＋1）a1 ＝N μ ＝a1b0 - a0b1 Step 2 给出a′系数公式a′0 ＝C（CM ＋BN） ＋a0B2 a′1 ＝（C - 1）（2CN ＋4Ba0）a′2 ＝- 2CM-B（C ＋1）N ＋2（- B2 ＋2（C - 1）2）a0 a′3 ＝2·（1 - C）·（2a0B ＋N）a′4 ＝M ＋B（N ＋Ba0）Step 3 给出b′系数公式b′0 ＝μ（C（M ＋Aa1） ＋Ba0（a1 ＋A）） ＋a0b0（a0 -1）（AC-B）b′1 ＝a0（2（C - 1）a1μ ＋（（C - 2）A ＋B）μ ＋（AB ＋2）b0 ＋Bb1） ＋C（A（（N - a1）b0 ＋μ） ＋b0（（a1 - a0）（a1 ＋a0） ＋1）） ＋2a20b0 b′2 ＝- 1（M ＋B（N - a1） ＋A（Ba0 ＋a0））μ ＋a0（（B-A）（a0 - 1）b0 ＋2（b1 ＋（C - 1）（b0A ＋b1 ＋μ）））b′3 ＝- a0b0AB ＋（- a20b1 - μ）A - a0（μ ＋b1）B -b0（（a0 - 1）2 ＋a1）b′den ＝（a0 - 1）·（- μb1 ＋b20）

改进后，需要在原有基础上预计算两个元素M，N，此时需要m ＋2s 的计算成本，但改进后对于a′多项式系数的计算成本为24m ＋5s，对于b′多项式系数的计算成本为47m ＋4s， 因此改进之后的显示公式的总计算成本为71m ＋9s，相对节省了27m ＋10s。

本文在windows 系统，CPU 为Intel（R）Core（TM）i5-8265U 的环境下，使用Python 语言对所提优化方法进行了编程实现，计算出了改进前后方法的使用时间，其中方法所需参数根据［5］所提供的代码选取的参数长度（30 位）随机生成，其对比由表4 给出。

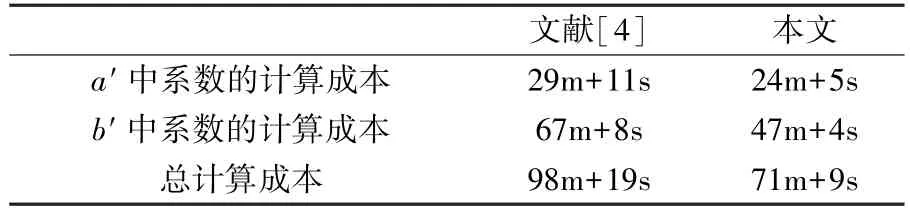
文献［4］ 本文a′中系数的计算成本 29m＋11s 24m＋5s b′中系数的计算成本 67m＋8s 47m＋4s总计算成本 98m＋19s 71m＋9s

由表4、5 可以看出，改进算法相比于原算法节省了27m＋10s 的运行成本，节省了12456ns 的时间。

python 程序运行时间（取100 组平均时间） 35273ns 22817ns

5 结束语

已有的（2，2）-同源算法中对于除子的Mumford 表示形式D（a′，b′） 中多项式系数的计算有非常复杂的公式，并且该部分的计算速度是主要影响整个（2，2）-同源的计算速度的关键。因此本文提出了对于计算实现方面的优化办法，即预先计算部分信息，并且与已有方法的计算成本进行对比。