基于颗粒流的膨胀土膨胀力时程细观机制研究

李涛, 黄晓冀, 刘波, 2, 张荣辉, 李幻

(1 .中国矿业大学(北京)力学与建筑工程学院, 北京100083;2.深部岩土力学与地下工程国家重点试验室, 北京100083;3.广州地铁设计研究院股份有限公司, 广东广州510010;4.华北水利水电大学地球科学与工程学院, 河南郑州450045)

0 引言

膨胀土在我国分布较为广泛,在天然状态下一般强度较高,压缩性低,易被误以为是较好的地基材料[1]。实际上因为其亲水性强、富含膨胀性黏土矿物,所以会随着土体含水率变化呈现出显著的胀缩变形特性[2-3],当膨胀变形受到约束时,会产生较大膨胀力,且随时间推移表现出增长趋势,一定程度时便会对周围结构或建筑物造成不可逆转的危害[4-5]。掌握增湿条件下膨胀力的变形规律,正确预估增湿状态下膨胀力的发展,是合理利用膨胀土进行地基充填、确保建筑物的长期稳定的关键,对于降低造价、保证工程质量有重要的实际意义。

膨胀力是衡量膨胀土基本性能的关键指标之一。国内外学者已对膨胀土增湿过程中的膨胀力开展了大量研究,研究内容主要围绕矿物成分[6]、初始干密度[7]、初始含水率[8]、温度[9]、孔隙比[10]等因素对膨胀土力学性质的影响。通过研究,学者们已经普遍认识到膨胀力主要取决于初始条件与其矿物成分含量。随着研究的深入开展,学者们意识到时间是膨胀力发展的重要影响因素,膨胀力随时间表现出一定规律。赖小玲等[11]通过开展膨胀力与微观结构试验,表明膨胀力随静置时间的增加不断衰减,衰减后期逐渐趋于稳定,且衰减效果与含水率和干密度有关;周葆春等[12]开展膨胀率试验得到膨胀率与时间的关系,即膨胀时程曲线,采用Logistic 函数描述膨胀时程曲线并取得较好的效果;叶为民等[13]考虑时间因素的影响,基于累积“楔力”与消散“楔力”相互累加的原理,得到了不同干密度膨胀土的膨胀力时程曲线的预测模型,并给出了参数的具体意义。以上研究表明,膨胀力随时间的曲线也与试样初始干密度、初始含水率等因素有关,但是这些研究均基于室内试验,从宏观角度对膨胀力时程曲线进行研究,缺乏细观层面对膨胀力的深入分析。颗粒流方法可以较好地实现从细观层面对膨胀土开展研究,故许多学者基于此出发,借助颗粒流软件开展相关研究。郑立宁等[14]考虑膨胀土的干湿胀缩效应,从颗粒间强度变化及颗粒体积胀缩入手进行数值模拟,通过控制颗粒密度与模量变化实现颗粒体积膨胀,对膨胀土路基在干湿胀缩循环下的破坏特征进行模拟研究;司马军等[15]考虑了土体抗拉强度随含水率的变化,设置模型中颗粒半径、颗粒胶结接触参数随含水率的变化,模拟了圆形薄层黏性土试样在粗糙边界条件下干缩裂缝的产生及扩展过程,定量分析了表面裂隙率,其模拟结果与室内试验结果较一致。Sima等[16]提出了基于黏土团聚体结构的团聚体收缩模型,通过设置收缩团聚体组合之间的接触来模拟黏土干燥收缩。Guo等[17]考虑了干燥过程中膨胀土颗粒间接触键与摩擦系数的强度折减,实现了对膨胀土干燥过程的模拟,研究了膨胀土干燥过程中强度变化与裂缝发育。上述学者们通过控制颗粒行为或者颗粒间的接触关系来实现膨胀土的数值计算,但是这些细观层次方面的研究,建立的模型少有考虑时间参数的影响。实际上膨胀土干湿过程中的的胀缩变形受时间影响明显,且颗粒胀缩影响着整个力学过程,这与目前的数值计算存在一定差异性。

针对上述问题,为了实现从细观层面开展膨胀力时程研究,本文中以成都膨胀土为研究对象,首先开展室内试验,对试验数据使用Knothe时间函数拟合得到膨胀率随时间变化的数学模型,引用体积应变的概念运算得到颗粒膨胀模型f(t),并进行了颗粒膨胀函数中参数b对时程曲线的敏感度分析。针对膨胀土材料的非连续性特征,借助PFC2D离散元软件,通过颗粒膨胀模型f(t)实现增湿过程中颗粒尺寸的控制,并依据室内试验进行细观参数赋值与验证,从细观层次上探讨了增湿过程中力链的分布特征,进一步揭示膨胀力变化机制。将数值计算结果与室内试验结果对比论证,为工程中通过控制膨胀土的膨胀特性以减小其工程危害及工程验算提供理论与应用参考。

1 膨胀力室内试验

1.1 试验材料与制样

试验所用土样来自成都东郊某建筑工地,取土深度在地表以下3 m左右。土中黏土矿物成分以伊利石和蒙脱石为主,占黏土矿物总质量的81%。试验严格按照《土工试验方法标准》(GB/T 50123—2019)规定进行,膨胀土物理力学性质见表1。可以看出,成都膨胀土自由膨胀率为59%,属于弱膨胀土。

表1 成都膨胀土主要物理力学性质Tab.1 Main physical and mechanical properties of Chengdu expansive soil

试验利用成都膨胀土扰动样制备重塑试样。现场取回扰动土样,将取回的土样压碎成小颗粒状,放入烘干箱烘干24 h,烘干后经过孔径为2 mm筛,按照目标含水率取蒸馏水与散土拌和均匀,将配置好的湿土装入塑料袋中密封 24 h,以保证湿土含水率均匀。而后根据目标干密度,精准称取配比好的散土,制成高度为20 mm的标准试样。试样初始含水率控制在最优含水率的两侧,分别为11.36%、14.48%、17.94%、21.97%,每组含水率下试样的干密度控制在1.5、1.6、1.7 g/cm3,试样方案见表2。

表2 试样方案Tab.2 Sample scheme

1.2 无荷膨胀率试验与膨胀力试验

膨胀土吸水产生膨胀。为了得到成都地区不同含水率条件下的膨胀特性变化规律,对成都膨胀土进行了不同初始含水率和干密度下的无荷膨胀率试验和膨胀力试验。

无荷膨胀率试验采用膨胀仪进行,测定干密度为1.6 g/cm3时,不同初始含水率w下的无荷膨胀率。具体过程为：将环刀固定在底座上,使试样底面与透水板顶面密切接触,一起放到水盒中,将多孔盖板放在试样顶面,对准中心,安放好百分表。之后往水盒中缓慢注入蒸馏水,使水自下而上浸入试样,记录不同时间下的百分表读数。当试样6 h内变形不大于0.01 mm时,证明试样变形达到稳定状态。

膨胀力测试方法有膨胀反压法、加压膨胀法及平衡加压法3种[10]。平衡加压法是在膨胀土开始膨胀时,逐步施加荷载来保持试样体积不变。平衡加压法过程基本不会引起土体内部结构破坏,可以更好地反映工程实际情况[18]。

膨胀力试验基于加荷平衡法在改进的单杠杆固结仪(见图1)上进行,具体过程为：

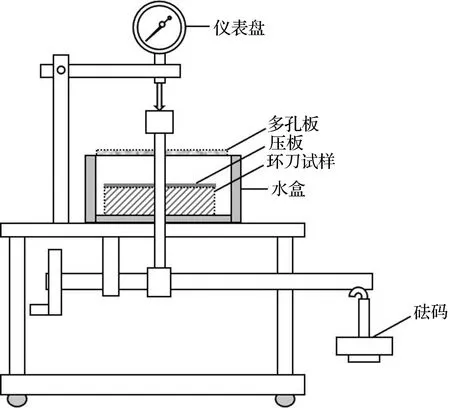
图1 改进的单杠杆固结仪Fig.1 Improved single lever consolidation instrument

步骤1：将制备完成的击实试样放入容器中,上、下放置上滤纸、透水板和盖板,安装百分表,施加1 kPa的压力,使装置各部分密切接触,保持稳定。

步骤2：往水盒中缓慢注入蒸馏水,过程中保持水面高出试样5 mm。

步骤3：试样开始膨胀后,对试样分级施加平衡荷载,使量表指针全程指向初始度数,施加荷载时注意慢速加压以免造成冲击力。

步骤4：当试样在某级平衡荷载下2 h内膨胀量不大于0.01 mm时,证明试样在该级荷载下达到稳定。记录不同时间下施加的平衡荷载。

制备的试验试样与试样膨胀力试验分别如图2、3所示。

图2 试验试样Fig.2 Test specimens

图3 试样膨胀力试验Fig.3 Expansion force test of test specimens

1.3 试验结果

通过上述试验,得到不同初始含水率下的无荷膨胀率数据以及不同初始含水率w和干密度下的膨胀力数据,计算后绘制关系图,得到的试样膨胀率与时间增长关系如图4所示。由图4可知,在试验初期(试验开始的3 h内),试样的膨胀作用表现明显,膨胀率时程曲线变形急剧增加,曲线较陡。随着时间的增加,膨胀趋势趋于缓和,增长速率降低,在试验后的3～12 h内进入缓慢增长阶段。试验开始12 h后,膨胀变形基本达到稳定,膨胀率随时间的增长趋势逐渐趋于平缓,并最终达到一个稳定值,即最终膨胀率。

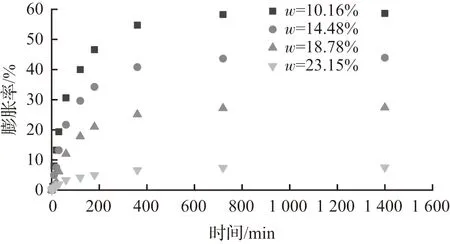
图4 试样膨胀率与时间增长关系图Fig.4 Expansion rate-time growth graph of test specimens

2 数值模型计算方法

2.1 颗粒膨胀模型的建立

PFC软件的基本思想是采用介质最基本单元——粒子和最基本的力学关系——粒子间的牛顿第二定律来描述介质的复杂力学行为[19],是从微观结构角度研究介质力学特性和行为的工具,它的基本构成为圆盘和圆球颗粒,计算时采用局部接触来反映宏观问题[20]。其主要研究思路为通过对颗粒的几何参数、接触特性等进行赋值,使颗粒模型介质体现的宏观参数与实际的宏观性质相匹配。采用球单元作为基本单元时,一般不需要单独赋予介质本构关系模型,仅需得到圆心及半径信息即可识别新的接触,故可以通过设定膨胀颗粒半径来开展数值计算。

一方面,膨胀土因富含亲水矿物而具有明显的遇水膨胀特性,若在体积膨胀变形过程中受到约束,就会产生膨胀力;另一方面,膨胀性土体细观结构多呈现出黏土颗粒黏结而成的叠聚体结构[21]。对成都膨胀土进行扫描电镜试验(scanning electron microscope, SEM)观察,其微观图像(见图5)表现出明显的叠聚体结构。采用离散元方法,将膨胀土整体离散为若干叠聚体(黏土团粒)如图6所示,赋予每个叠聚体单元尺寸参数,并通过颗粒半径R随时间的变化规律来模拟膨胀土增湿过程中颗粒尺寸的变化。

图5 试样SEM图像(×2 000)Fig.5 SEM image of test specimen (×2 000)

为了得到膨胀变形和时间的关系,使用Knothe时间函数对无荷膨胀率试验结果进行拟合。Knothe时间函数最初被用于地表动态移动预测研究中[22],后续学者们尝试用其对膨胀土时程曲线开展拟合分析,得到了较好的拟合效果[23]。对试验前120 min内的无荷膨胀率试验结果利用Knothe 时间函数模型进行拟合分析,拟合公式为

δe=a(1-e-bt),

(1)

(2)

式中：δe为时间为t(min)时对应的无荷膨胀率;a、b为待定的拟合参数(0≤a,0≤b≤1)。

通过最小二乘法拟合得到的系数及相关系数见表3。由表3中结果可见,不同初始含水率条件下的无荷膨胀率数据的拟合相关系数均R2>0.9,说明在一定的初始含水率条件下,Knothe函数可以较为有效地对成都膨胀土的膨胀力与时间的关系进行预测。

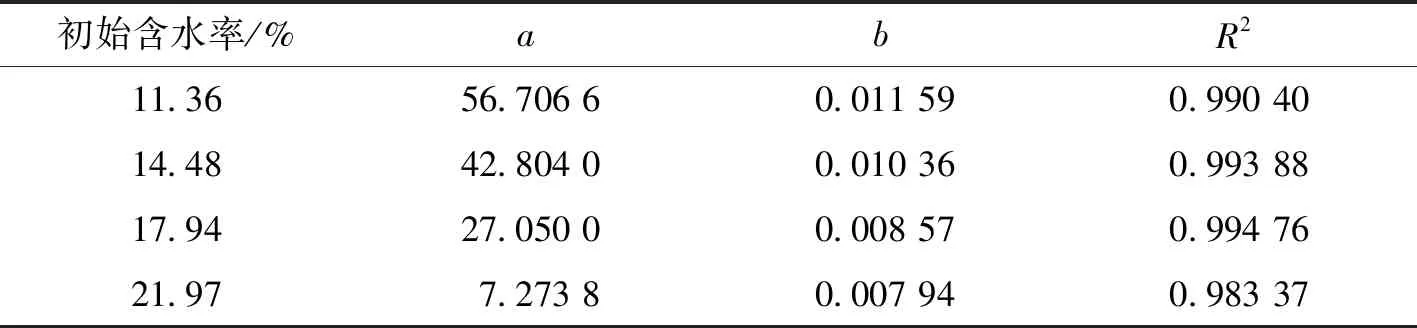
表3 不同含水率下的拟合系数Tab.3 Fitting coefficients under different water content

从式(1)可知,当t趋于无穷时,膨胀率可近似为

δe=a,

(3)

因此,参数a的意义为膨胀土试样的最终膨胀率。对比拟合得到的a值与试验得到的最终膨胀率,验证了这一意义。同时由式 (2) 可知,参数b反映了体积膨胀的快慢。

假设增湿过程中颗粒半径随时间变化满足函数f(t),使得

R=R0f(t),

(4)

式中：R0为初始状态的颗粒半径;f(t)为膨胀土颗粒在t时刻的膨胀率;R为增湿过程中t时刻对应的颗粒半径。由于膨胀土颗粒实际尺寸较小,因此假设所有土颗粒能够均匀吸水,即每个颗粒遵循相同的膨胀规律,则在二维条件下膨胀土试样的宏观膨胀应变可以表示为

εv=f2(t)-1,

(5)

式中εv为时间为t时试样对应的宏观体积应变。

在满足上述条件时,颗粒膨胀率f(t)可以由t时刻土体宏观膨胀应变εv表示为

(6)

由体积应变和膨胀率的定义可知εv=δe。联立上式得到考虑体积应力的颗粒膨胀函数f(t)为

(7)

2.2 数值模型的建立

膨胀土颗粒尺寸的设置和接触模型的选取是数值模拟的关键;然而在常规数值模型建立时,往往忽略了增湿过程中颗粒膨胀带来的影响,而膨胀土颗粒的胀缩行为影响着整个力学过程,因此本研究在建立数值模型时,通过内置的fish语言将式(7)的颗粒膨胀函数f(t)写成可读入文件导入PFC2D中,设置颗粒圆盘尺寸随时间的变化来模拟颗粒膨胀特性,实现了对膨胀土增湿过程影响的数值模拟,进而分析增湿过程中不同干密度和初始含水率下膨胀力的时程特征。

值得注意的是,膨胀土的膨胀行为极大地受黏粒含量的影响。目前的研究结果表明,膨胀特性与各类黏粒矿物组成含量[24]、混合层矿物[25]以及黏粒的颗粒排列[26]等有关。自由膨胀率与黏粒含量之间离散程度较高,大量试验数据无法得到合适的拟合关系,难以建立考虑黏粒含量的可靠模型[27],因此,在建立数值模拟时未考虑膨胀土黏粒含量的影响。

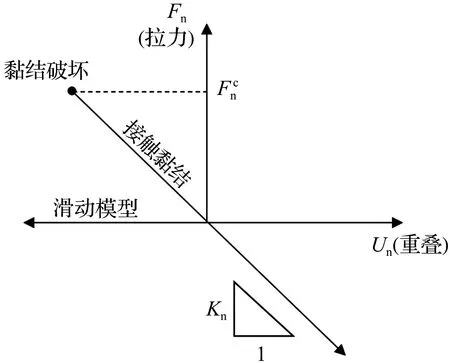
图7 接触黏结模型本构示意图：法向/切向接触力分量Fig.7 Constitutive diagram of contact bond model：normal/tangential contact force component

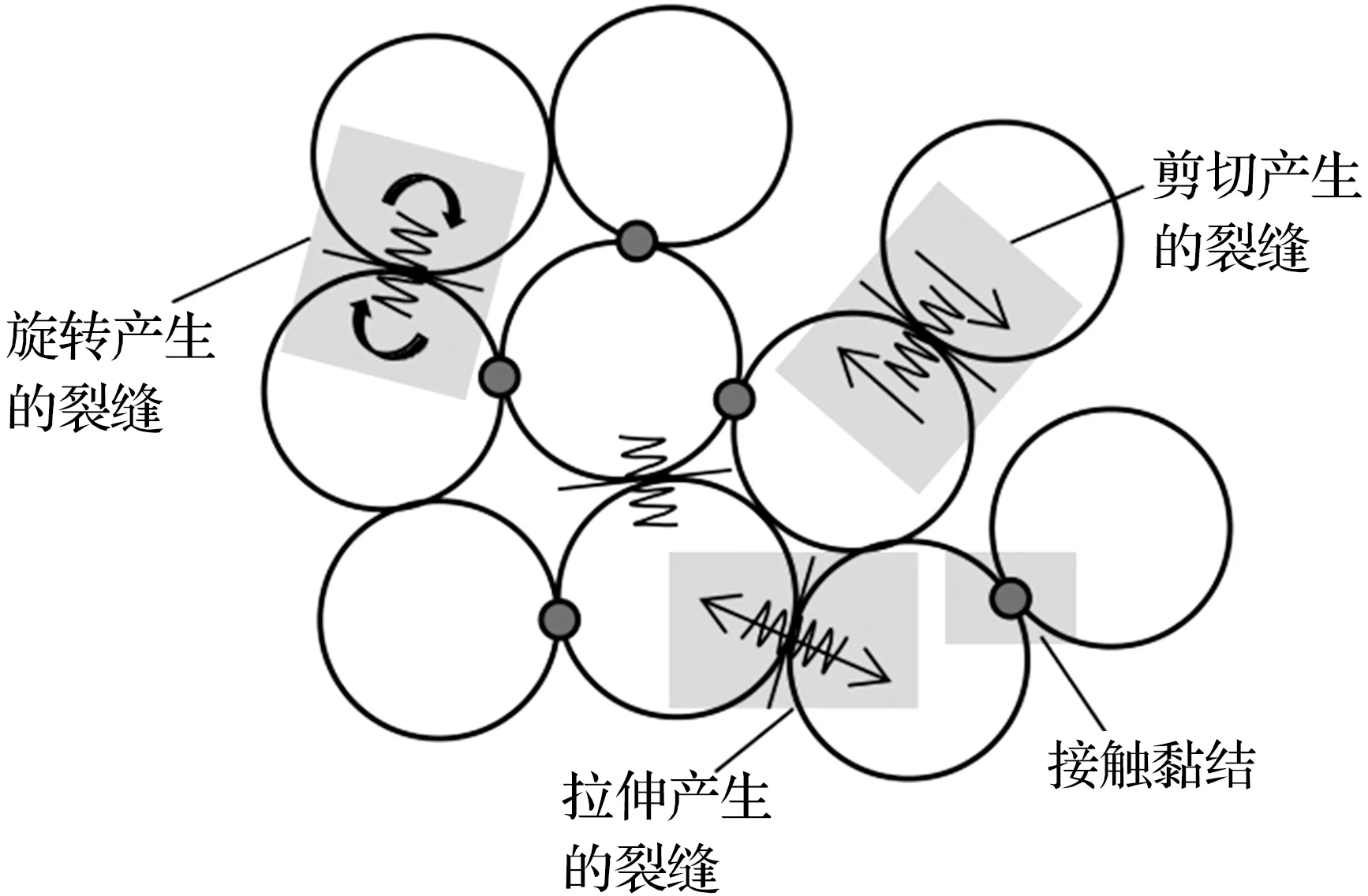
图8 接触黏结模型示意图Fig.8 Schematic diagram of the contact bond model

由于膨胀土在增湿过程中颗粒持续膨胀,因此在接触黏结模型的基础上,考虑膨胀性颗粒产生的强度衰减,以模拟增湿过程中颗粒膨胀对力学特性的弱化效应[14]。依据室内试验的试样尺寸与边界情况,建立尺寸为31.9 mm×20 mm(长度×宽度)的膨胀力试样模型(即标准固结试样),再按照以下顺序建立数值模型：

①生成初始模型：建立墙体,按照式(7)在墙体范围内生成随机生成土样颗粒。

②设置接触模型：在颗粒间设置接触黏结模型,设置颗粒黏结参数。

③调整内应力,不断调整模型的边界,使颗粒体系间内应力均匀且处于低水平状态。

④不断调整颗粒单元属性参数与颗粒黏结属性参数,生成最终的膨胀力试样数值模型如图9所示。

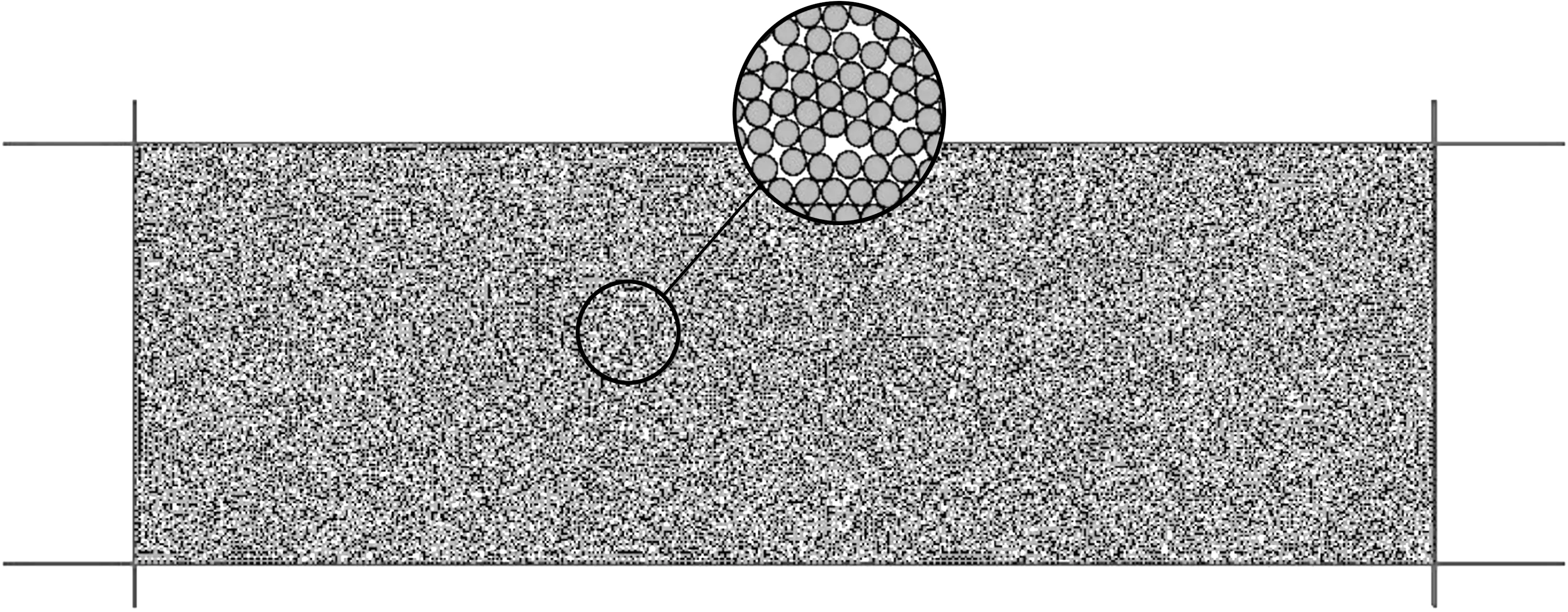
图9 膨胀力试样数值模型Fig.9 Numerical model of expansive force sample

2.3 细观参数的设置与验证

在 PFC2D 中对模型的细观参数设置主要包括颗粒单元属性参数和黏结属性参数,颗粒单元属性参数主要包括最小粒径、粒径比、颗粒密度、接触模量、刚度比、摩擦系数等。黏结属性参数主要包括法向黏结强度和切向黏结强度2个参数。采用试错法[29]确定膨胀土细观参数的赋值,通过与室内试验获得的膨胀力力学参数进行对比,使所建立的颗粒流模型和室内试验所获得的宏观力学结果一致。

随着含水率的增加,黏粒表面结合水膜增厚,膨胀土颗粒在土样体积限制的条件下膨胀挤密,填充土体内部孔隙。当含水量增大到一定程度后,孔隙中开始出现自由水,伊-蒙混层羽翼状的边缘被水化,土颗粒间的水膜联结作用减弱,黏结强度降低,同时自由水充斥于土体孔隙中充当润滑作用,削弱了土颗粒之间的摩擦力[30-31],增湿过程中膨胀土颗粒强度弱化模型如图10所示。故结合文献[14]研究结果可知,在颗粒流中考虑颗粒强度在循环运算中不断降低,其中黏结强度降低60%,摩擦系数降低50%。考虑颗粒产生体积膨胀对颗粒密度和模量产生的影响,在确定微观参数时,参考成都地区膨胀土相关研究的参数选取结果[32-33],通过颗粒流试验匹配膨胀土膨胀力试验结果[34-35],得到颗粒流模型的基本细观参数见表4。

表4 颗粒流模型基本细观参数Tab.4 Basic mesoscopic parameters of particle flow model

采用强度对比的方法来进行颗粒流模型细观参数的验证。表4中细观力学参数下的颗粒流模型得到的宏观力学参数,与室内试验得到的宏观力学参数进行对比,室内试验与数值模拟结果对比见表5。由表5可知,不同含水率下最终膨胀力误差范围较小,误差绝对值在1.82%～6.67%,误差范围较小,因此数值模拟与室内试验在膨胀力强度参数上相吻合,证明了基于颗粒膨胀模型建立的颗粒流数值模型及细观参数的合理性。

3 颗粒流时程结果分析

3.1 膨胀土颗粒接触力变化规律

颗粒体系与流体、均匀固体不同,颗粒作为离散体,其受力通过颗粒体系传递。图11所示分别为膨胀土增湿过程中颗粒间的接触力,其中线条的粗细显示了接触力的大小,线条越粗,则接触力越大。在膨胀土的增湿过程中,试样内部颗粒接触力发生改变,尤其是试样中心位置的颗粒接触力变化较大。膨胀土的膨胀填充了试样的空隙,随着膨胀土含水量的增加,土体有继续膨胀的趋势,由于固定边界使颗粒收到挤压,因此随着挤压变形的加大,颗粒间产生法向应力,土体产生膨胀力并持续增大。同时,颗粒间产生的膨胀力又会进一步限制颗粒的膨胀。图11表明：增湿过程中膨胀土膨胀力从0增加到90 kPa,并最终稳定在该状态下的最终膨胀力值。

(a) P=0 kPa

3.2 时程曲线计算结果分析

不同初始含水率不同干密度膨胀土的数值试验与室内试验膨胀力时程曲线如图12所示。从图12(a)中可以看出：随着初始含水率的增加,极限膨胀力逐渐减小;由图12(a)、(b)可知,随着干密度的减小,相同含水率膨胀土对应的膨胀力也随之减小。

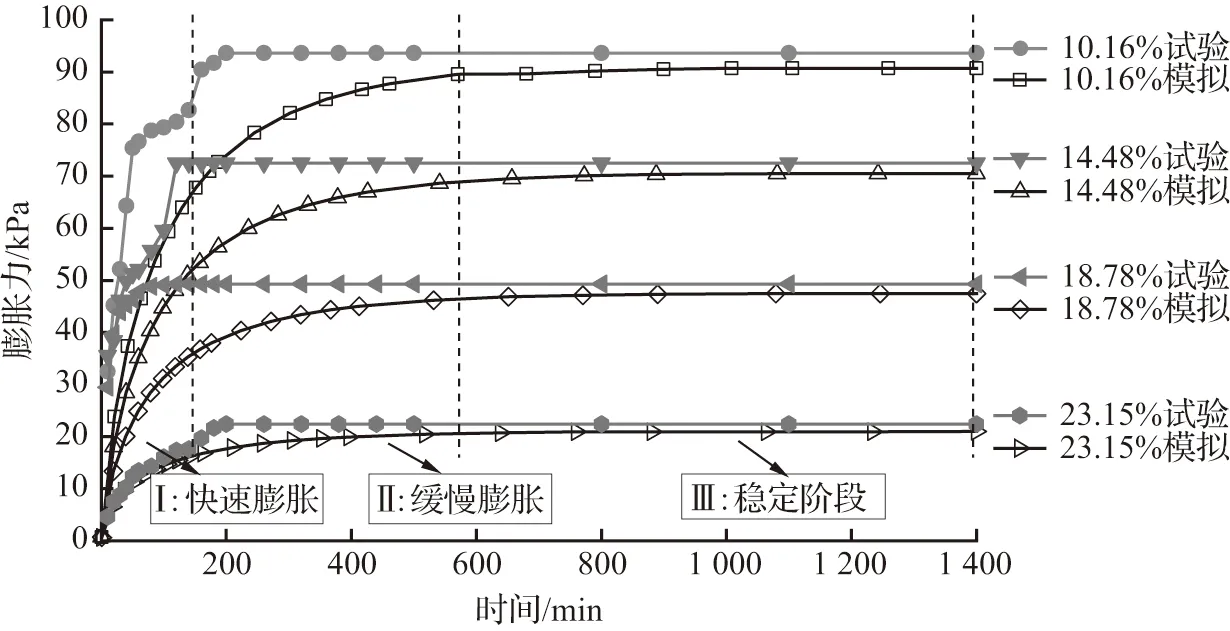
(a) ρd=1.7 g/cm3

通过对试样膨胀力的测定可知,随着时间的增长,膨胀力逐渐增长并趋于稳定,膨胀力随时间的关系曲线如图12所示。图12可见,增湿过程中,不同初始含水率下的膨胀土的膨胀力均随时间的增长而增加,达到1 400 min时试样膨胀力趋于稳定。时程曲线经历了从斜直线→凸弧线→平直线的变化过程,可以将膨胀力随时间变化分为3个阶段：快速膨胀阶段Ⅰ,膨胀速度曲线在最初阶段近似于直线,并在0～2 h内膨胀力达到极限膨胀力的80%以上;缓慢膨胀阶段Ⅱ,曲线特征为一段外凸的弧线,一般在2～7 h,此阶段达到极限膨胀力的95%以上;稳定阶段Ⅲ,至试验结束膨胀力不再有太大变化,达到相对稳定状态。

数值试验结果与室内试验结果基本相同,并且与文献[36]对云桂铁路中膨胀土研究得出的结论基本一致,也与文献[37]得到的不同干密度下膨胀力随时间的增长趋势相同,表明干密度是膨胀力时程曲线重要的影响因素之一,说明在建立数值模型时,引入颗粒膨胀模型较好地考虑了增湿过程中颗粒膨胀的影响。从膨胀土细观颗粒角度出发,得到的宏观膨胀力时程曲线具有可靠性,再次验证了理论模型的正确性。

由图12可知,干密度一定时,初始含水率越低,初始膨胀速率越大,初始含水率越高,初始膨胀速率越小。由文献[38]可知,土体含水率越小,土的基质吸力越大,增湿过程中土体的基质吸力随含水率的增加而减小,颗粒间黏结力也随之减弱,导致土体颗粒向外扩张,引起土体体积膨胀,因此,同一干密度试样的初始含水率越小,增湿初始阶段基质吸力越大,土体初始阶段膨胀力增长就越快。

膨胀土试样膨胀力产生上述规律的主要原因是：干密度相同时,初始含水率越低,膨胀土中亲水性物质如蒙脱石、伊利石等吸水就越不充分,膨胀势能就没有得到充分释放,绝大部分膨胀势能储存在土体中;而当试样初始含水率较大时,膨胀势能已经部分释放,剩余的膨胀势能较小,吸水后表现出来的膨胀力就相对较小[33]。

4 膨胀参数b敏感度分析

由前述,对无荷膨胀率试验数据拟合得到的关于时间的膨胀率时程曲线中包含a和b2个参数,参数a的实际意义为最终膨胀率,且在膨胀率时程曲线中有较明确的体现,故本章仅对参数b开展敏感度分析。

公式(1)中膨胀函数f(t)所包含的参数b对膨胀率计算有一定影响。为了探究参数b对膨胀土膨胀率曲线的影响,以干密度ρd=1.6 g/cm3,初始含水率分别为11.36%、14.48%的膨胀土为例,参数b的讨论范围参照试验数据拟合结果,确定为0.007～0.010,分析参数b在3种情况下膨胀率时程变化特征,得到膨胀力时程曲线随参数b值变化情况如图13所示。

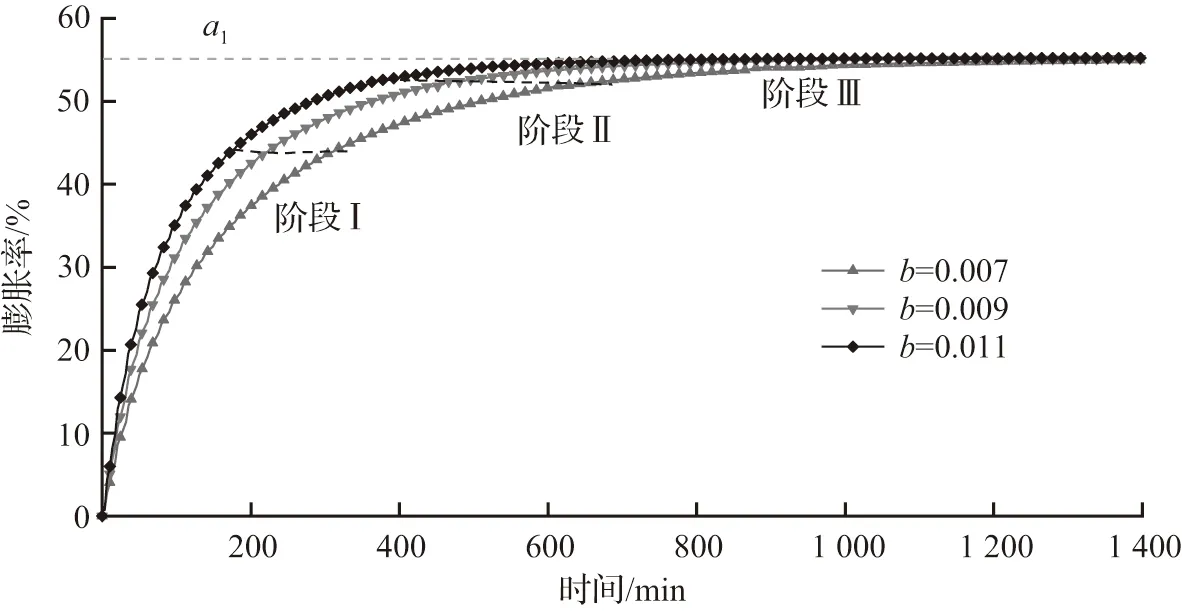
(a) w0=11.36%

图13可知：膨胀率时程曲线可按照增长程度划分为快速增长阶段Ⅰ、缓慢增长阶段Ⅱ和平稳阶段Ⅲ,最终收敛达到对应的最终膨胀率a值。同一时刻,膨胀率随b值的减小而减小,随b值的增大而增大。b值越小,膨胀时程曲线达到收敛状态所需时间越长;b值越大,膨胀时程曲线达到收敛状态所需时间越短。参数b值对膨胀时程曲线的初始增长率影响较大,初始膨胀速率与b值大小呈正相关。

当参数b=0.007时,阶段Ⅰ完成时间在1～3 h,阶段Ⅱ完成时间在3～7 h。参数b在3种情况下,膨胀率曲线均能达到收敛状态,即试验结束时计算模型能达到最终膨胀率。最终膨胀率只与初始含水率和干密度有关,不受该范围内参数b大小的影响。选取的参数讨论范围未能出现膨胀率曲线不收敛状态。

5 结论

①通过对膨胀土增湿过程膨胀力的数值模拟,从细观角度揭示了膨胀土在增湿过程中颗粒接触力的变化特征,与室内试验结果对比分析,数值模拟结果准确,表明了基于颗粒膨胀模型开展所建立数值模型的合理性。

②同一初始含水率下膨胀力随干密度增大而增大,且初始含水率越小,膨胀力随干密度的变化速率越大;同一干密度下,初始含水率越小,极限膨胀力越大。膨胀力时程曲线具有明显的三阶段特征,增湿过程膨胀力变化经历快速膨胀、匀速膨胀、相对稳定3个重要阶段。快速膨胀阶段大致为0～2 h,此时膨胀力可达到极限膨胀力的80%;匀速膨胀阶段在2～7 h,此时膨胀力可以达到限膨胀力的95%。

③当膨胀率时程拟合公式(1)中参数b≥0.007时,膨胀率曲线均能收敛;当参数b<0.007时,膨胀率曲线不能收敛。b值越大,时程曲线这3个阶段越明显,时程曲线越显凸形。参数b值对膨胀力增长速率影响明显,初始膨胀速率与b值大小呈正相关。

④考虑体积应力的膨胀土颗粒计算模型,可以很好地预测增湿过程中膨胀力的变化。膨胀土颗粒遇水会出现膨胀变形和软化问题,在二者共同影响下形成膨胀土特有的物理力学性质,故在后续的膨胀土模型研究应该充分考虑颗粒软化的影响。