基于LCOE 模型的光伏发电项目优化研究

陈柯延

（国网江苏省电力有限公司宝应县供电分公司， 江苏 扬州 225800）

0 引言

方阵倾角的提升会使光伏方阵的荷载随之增加，需要对光伏发电的支架和基础予以强化处理，初始投资会相应提升。因方阵倾角不断提升，光伏发电的发电量也会呈现出先升后降的状态，并且在某一倾角时的发电量为最高。方阵间距的提升会使光伏发电项目的占地面积、电缆长度随之增加，导致初始投资增加。因方阵间距的不断提升，其阴影覆盖损失便会随之降低，故发电量呈上升趋势。方阵间距和方阵倾角的提升会对光伏发电站初始资金以及发电量产生影响，光伏发电站的经济效益也会因此受到影响。准确找到方阵倾角和方阵间距之间存在的最佳组合，便可以有效实现光伏发电站利益最大化目标[1]。但是，由于光伏发电站之间存在差异性，因此，达到利益最大化效果的方阵倾角和方阵间距最佳组合也可能不同。

1 基于LCOE 的光伏发电成本模型

光伏发电成本普遍会用LCOE（即平准化度电成本，公式中记为CLOE）来指代，是用于评价各类发电系统在某一运作期限内电力单位所需成本的净现值。在发电系统的运作期间，每度电所需要的成本值为总成本投入贴现值与总发电量收益贴现值之比。针对光伏发电系统，LCOE 数值的高低便可以明确地展示出光伏发电项目的实际发电成本以及经济效益情况，是相关人员进行投资计算、并网电价指导等工作的重要参考，极具指导价值。基于LCOE 模型的光伏发电成本计算公式如下：

式中：I0为初始投资成本；At为第t年的运营总支出（包含土地租金）；M为当年发电量；i为投资收益率；n为财务分析过程中的系统年数；t为系统运行周期（t=1，2，3，…，n）。由式（1）可知，LCOE 模型以动态模拟为基础进行构建，在计算时考虑了贴现率对LCOE值的影响。

2 方阵间距和方阵倾角最佳组合的计算方法

计算各个方阵间距中差异性方阵倾角的实际发电量，以此确定差异性方阵间距中发电量最大的方阵倾角，进而获得多个方阵间距和方阵倾角组合。然后，根据众多组合的初始投资、运维成本和发电量等因素，分别计算每个组合的经济性指标，再对经济性指标进行比较，找到最终可以实现光伏发电项目利益最大化的方阵间距和方阵倾角最佳组合。

3 实例分析

本文实例分析是在土地成本影响的基础上，以某地面集中光伏发电项目为例，分别根据传统的计算方法和上文阐述的计算方法，对该光伏发电项目的经济性指标予以计算和对比，找出最具经济价值的方阵间距和方阵倾角最佳组合，同时验证该利益最大化方法的可行性，进而实现光伏发电项目优化设计目标。

为简化分析，本文做出以下假设：

光伏发电项目的可使用场地面积不存在局限性、各个方阵倾角支架以及基础均为原定、电缆长度不变、方阵倾角的变化只对发电量和占地面积产生影响、各个方案的初始投资均为一致、年度运维成本和单位土地成本在经营周期内维持原定。

本文通过LCOE 模型对光伏发电项目单位的发电量成本情况进行评价，LCOE 数值越小，便证明优化设计方案最佳。

3.1 项目概况

该光伏发电项目的地理坐标为北纬30.62°，东经114.13°，且占地场所为平地，该项目的装机容量为1 004.4 kW，投入使用期限为25 年，建设成本为4.2 元/Wp，折现率为6.5%，年度运维成本为0.05 元/Wp，光伏组件年度衰减率为0.5%，所得税税率为25%，增值税税率为13%，折旧年限为20 年，残值率为5%。

该光伏发电项目运用的组件规格为2 568 mm×1 088 mm（长×宽）的450 Wp 单晶硅组件，具体应用数量为2 400 块，在运用过程中，将每12 块组件进行串联，制成200 串组串。该项目方阵方位角的度数为0°，且应用了固定支架的设计，并按照竖向两排的标准进行配置，同时，将每48 块组件予以组合排列，利用此方法建出50 个方阵。组件和组件之间务必预留出20 mm 的缝隙，尽量降低方阵面上的风压。选择13 台65 kW 的组串式逆变器，且所有逆变器均需具备四路MPPT（最大功率点跟踪）。同时，在各路MPPT 上接入3～4 串组串。

3.2 应用传统方法予以优化设计分析

3.2.1 计算倾斜面总辐射量最大时的方阵倾角

计算可得该光伏发电项目所处位置的倾斜面接收总辐射量最大时的方阵倾角为22.7°，总辐射量为1 287 kW·h/m2，如图1 所示。

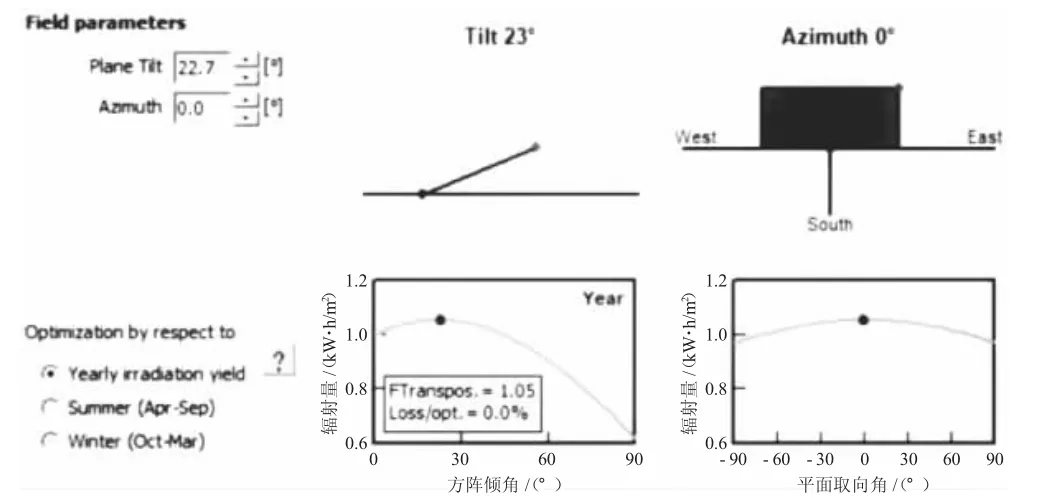
图1 倾斜面总辐射量最大时的倾角

3.2.2 计算方阵前后排间距

通过计算得到方阵倾角，对方阵前后排的间距进行计算，利用一般设计原则明确其数值为8.56 m，方阵东西走向的长度为25.67 m，单方阵的占地面积为219.78 m2，光伏发电场地所占面积为10 988.94 m2。

3.2.3 明确发电量最大时的方阵倾角

通过计算得到方阵间距数值，在全部电量损失因素的基础上，对方阵倾角予以优化设计，如图2 所示，实现并网电量最大化[2-3]。

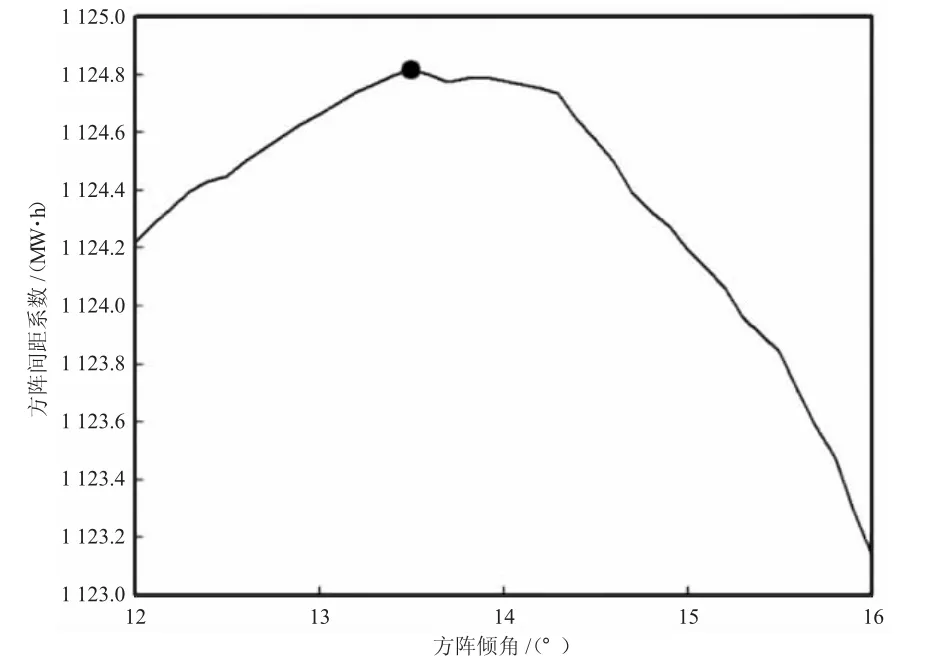
图2 发电量仿真二次优化设计示意图

3.2.4 计算优化方案的经济性指标

根据传统的计算方法，确定方阵间距，其数值为8.56 m，方阵倾角为13.5°，第一年发电小时数为1 041.48 h，光伏发电场地所占面积是10 988.94 m2。各个光伏发电站单位土地租金时的LCOE 如表1 所示。

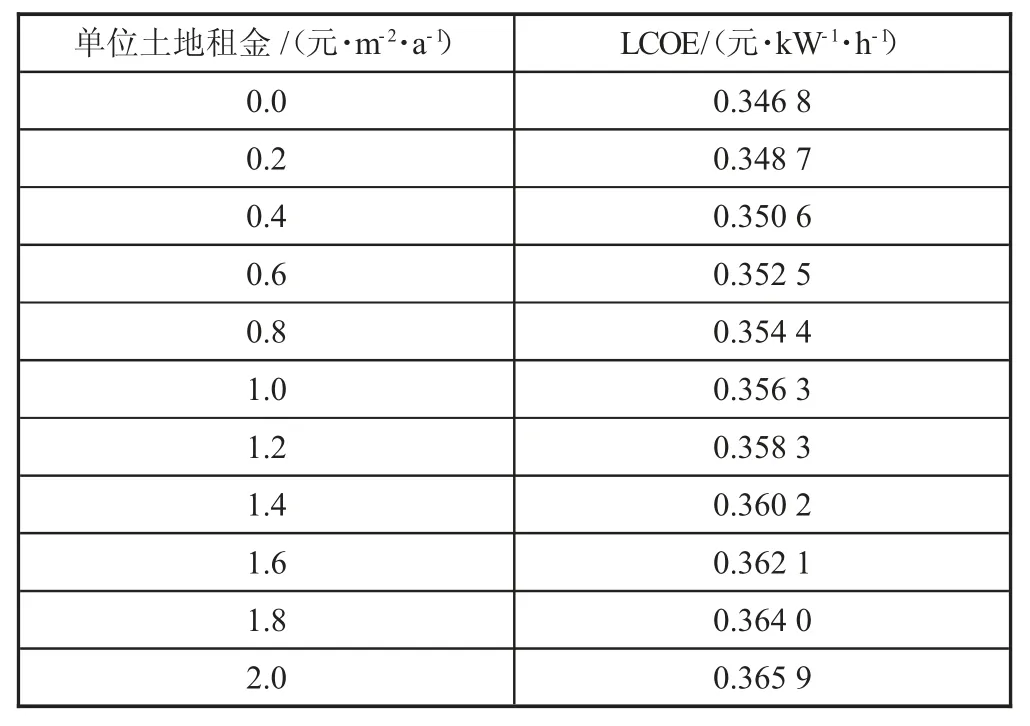
表1 各个光伏发电站单位土地租金LCOE

3.3 应用方阵间距和方阵倾角最佳组合计算方法分析

3.3.1 寻找不同方阵间距下发电量最大时的方阵倾角

本案例分析应用的方阵间距参数在7.0～14.0 m之间，步长为0.5 m。对各个方阵间距下差异化方阵倾角的发电量进行计算，得到全部方阵间距和发电量最大时的方阵倾角组合。发电量最大时的方阵倾角和第一年发电小时数如图3 所示。

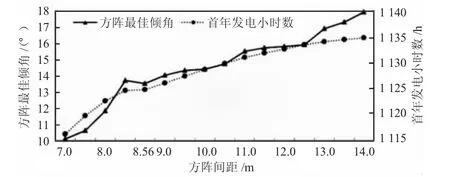
图3 发电量仿真二次优化

3.3.2 计算全部组合的经济性指标，得到最佳组合优化方案

先依照方阵间距的东西、南北走向间距，计算各个南北走向的方阵间距单个光伏方阵的占地面积，将得到的结果和方阵数量相乘，可得到不同南北向间距光伏发电项目的整体占地面积[4-5]。由于方阵南北向的间距会呈现出扩大趋势，单个方阵的占地面积和光伏发电项目的总占地面积也会因此扩大。各个方阵南北向间距单个方阵和光伏发电总占地面积参数如表2 所示。

表2 各个方阵南北向间距单个方阵和光伏发电总占地面积参数

依照每个方阵南北走向间距下的发电量最佳方阵倾角、光伏发电项目整体占地面积和土地单位租金，计算全部优化方案下的年土地租金，年土地租金的数额会因方阵南北走向间距和单位土地租金数额的提升而增加。

对得到的全部方阵南北走向间距下的发电量最大时最优倾角、第一年发电总时间（h）、光伏发电项目整体占地面积和土地租金数额等进行经济性指标计算，可得全部组合方案的LCOE，以此获得方阵间距和方阵倾角的最佳组合，实现光伏发电项目的优化目标[6]。计算结果如表3 所示。

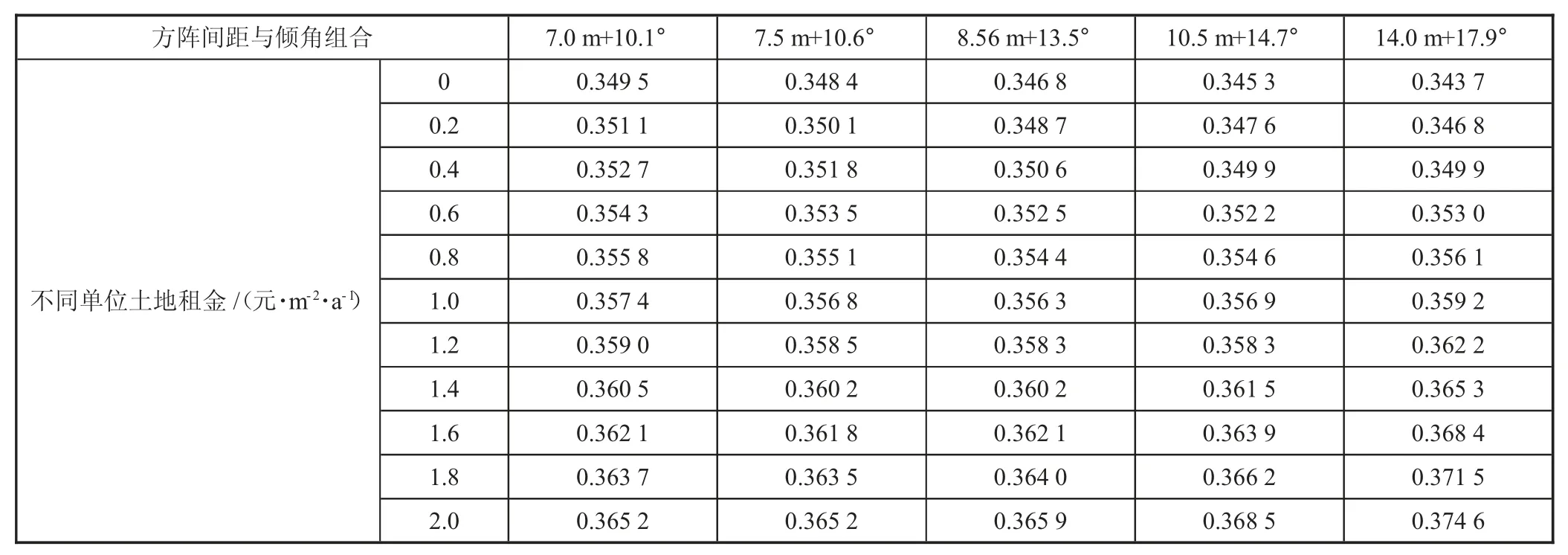
表3 各个方阵间距与倾角组合、不同单位土地租金时的LCOE 计算结果 元/（kW·h）

对计算结果进行分析，在相同的方阵间距和方阵倾角条件下，LCOE 的数值会因单位土地租金的增加而升高。以“7.0 m+10.1°”组合为例进行分析，单位土地租金由0.0 元/（m2·a）增加至2.0 元/（m2·a），LCOE 的数值由0.349 5 元/（kW·h）增加至0.365 2 元/（kW·h）。单位土地租金呈逐渐上升趋势，LCOE 最低优化方案的方阵间距和方阵倾角呈下降趋势。随着单位土地租金的增加，LCOE 最低方案的方阵间距和方阵倾角组合由“14.0 m+17.9°”变成“7.5 m+10.6°”。传统方法计算得出的方阵间距和方阵倾角最佳组合为“8.56 m+13.5°”，其LCOE 的数值只在单位土地租金为0.8元/（m2·a）时才最低。各个单位土地租金时的方阵间距和方阵倾角最佳组合如图4 所示。

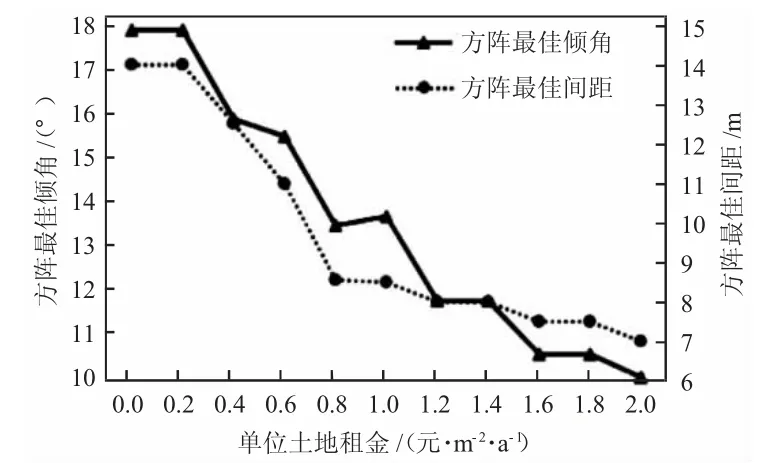
图4 各个单位土地租金时的方阵间距和方阵倾角最佳组合

4 结论

1）利用传统方案设计并计算得出的方阵间距与方阵倾角组合，并非经济性指标的最佳组合。土地租金会对光伏发电项目的方阵间距和方阵倾角优化设计方案造成影响，且随着土地租金的不断变化，其经济性指标最佳优化设计方案的方阵间距和方阵倾角可能会存在差异性。

2）在相同的方阵间距和方阵倾角条件下，LCOE的数值会因单位土地租金的增加而升高。不仅如此，因单位土地租金呈逐渐上升的趋势，使得LCOE 最低优化方案中的方阵间距和方阵倾角呈下降趋势。

3）为简化计算，本研究对各个方阵间距和方阵倾角组合的项目初始投资予以相同假设。但事实上，光伏发电项目的方阵间距和方阵倾角的变化会对支架、基础和电缆等内容形成相应的影响，进而使得项目初始投资也随之产生变化，并且普遍会以相同的方向予以变化。因此，综合考虑以上因素，LCOE 数值呈最佳状态时对应的方阵间距和方阵倾角组合将会比本研究的计算结果低。

4）本研究的背景是光伏发电项目的场地可用面积不会受到限制、总装机容量固定、支架固定、平地以及正南朝向等。针对所占场地可用面积固定、总装机容量非固定、跟踪支架、地形、坡度和朝向均不固定的情景因素，也可以利用以上方法进行研究。