三层金属矩形狭缝阵列透射峰的分裂与合并
龙 庆 沈宏君 王叶壮 陈俊坤
(宁夏大学物理与电子电器工程学院,宁夏 银川 750021)
0 引言
当电磁波照射到金属表面时,在高频电磁场驱动下,金属表面的自由电子会随之振荡。当入射光频率与金属表面传导电荷的集体振荡频率相匹配时,在具有自由电子的金属表面或附近会产生表面等离子激元(Surface Plasmon Polaritons,SPP)[1-2]。1998年,Ebbesen 等[3]首次观察到光在通过具有二维亚波长金属孔阵列的金属薄膜时出现异常透射现象(Extraordinary Optical Transmission,EOT)。基于阵列周期决定透射峰波长位置的特点,Ebbesen 等将EOT 现象与表面等离子激元联系在一起。迄今为止,有学者对异常透射背后的物理机制提出多种解释[4-7]。大多数学者研究认为,这种透射增强是由孔周围的波纹支持表面等离子激元(SPP)共振激发的。此外,还有一些研究人员认为,金属狭缝内的法布里-珀罗(FP)模共振也有可能导致透射增强[8-10]。2011年,Guillaumée等[7]发现了由Fabry-Perot模和表面等离子体模混合成的透射模,能很好地将FP 理论与表面等离子体理论结合起来。除了对EOT机理进行研究外,EOT 现象被广泛应用于磁光法拉第器件[11]、传感器[12]、太阳能电池[13]、光导天线[14]等领域。
综上所述,已有的研究主要集中在双层金属膜亚波长周期结构的EOT特性领域。为研究中间金属层几何参数与边界金属层几何参数对透射谱的影响是否相同,本研究设计出由两个空气层间隔开的、含有三个矩形狭缝阵列金属薄膜的金属光栅。在可见光和近红外区域,通过改变各金属层的厚度、狭缝宽度和空气层厚度,可以利用有限元法(Finite Element Method,FEM)来研究光通过多层薄膜的传输行为。研究发现,透射谱中主要存在四个共振峰,可将其分为三类,即表面等离子共振峰、FP 共振峰和FP-SPP耦合模。当狭缝宽度、层间距和薄膜厚度发生改变时,会对透射谱产生明显的影响,且中间金属层几何参数和边界金属层几何参数的改变对透射谱产生的影响不同。
1 结构模型
本研究设计的带有周期性亚波长矩形狭缝的金属/空气多层膜结构如图1所示。空气层的厚度分别为D1、D2,金属层的厚度分别为H1、H2、H3。该结构左右两侧设有周期边界,金属层和空气层具有相同的光栅周期p,金属层的材料为银。在研究中间金属层与边界金属层不同对透射行为产生的作用时,只讨论狭缝位置不变、固定周期p=200 nm 情况下,不同金属层几何参数变化时产生的影响。而光栅周期p[15]和狭缝横向位移[16-17]同样会对透射谱产生明显影响。
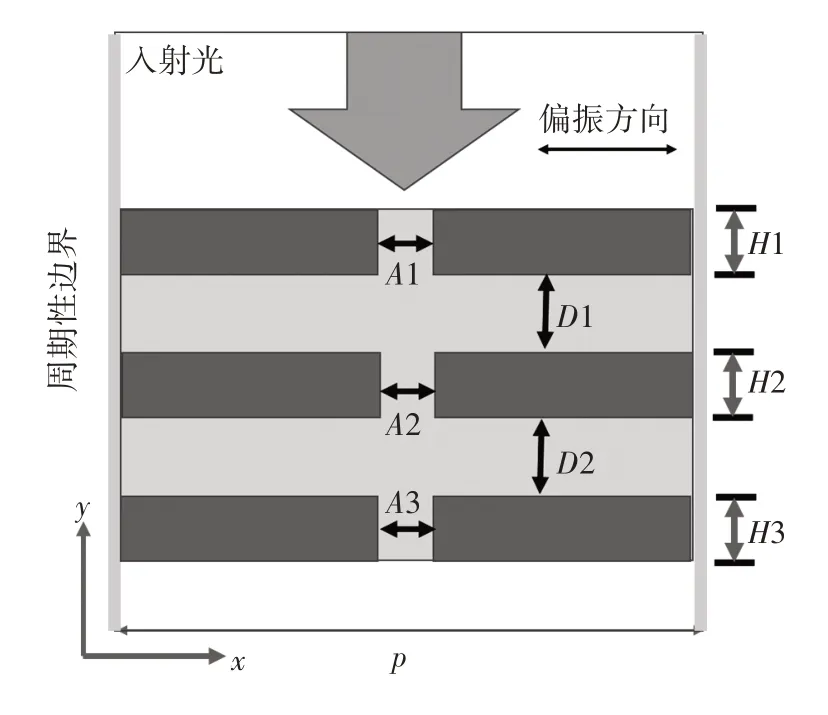
图1 具有周期性亚波长缝阵列三层金属膜结构
入射光沿y方向入射,产生具有电场分量Ex、Ey和磁场分量Hz的线偏振平面波。金属银的介电函数采用忽略电子振荡的自由电子气模型,即洛伦兹-杜鲁德模型[18],介电常数表达见式(1)。
式中:ω为入射光角频率;截止频率ε∞=2.406 4;等离子体振动频率ωp=2π×2 214.6×1 012 Hz;系数Δ = 1.660 4;室温下电导率γ= 2π × 4.8 ×1.12 Hz;晶格离子的平均振动频率为Ω= 2π × 1 330.1 ×1 012 Hz;电子与晶格离子的碰撞时间为Γ=2π ×620.7 × 1 012。银的折射率为复数,实部用来描述银对光的折射特性、虚部用来描述银对光的吸收特性。将空气填充到金属缝隙中,使其围绕结构,其介电常数取εair= 1。
2 数值结果分析与讨论
设定银膜的厚度H1=H2=H3=200 nm、光栅周期p=200 nm、空气层厚度D1=D2=100 nm、第一层金属狭缝宽度A1=30 nm,通过改变第二层和第三层金属狭缝宽度,得到透射谱如图2所示。图2(a)为第二层金属狭缝宽度A2为10 nm、20 nm、30 nm、40 nm、50 nm时的透射光谱,图2(b)为第三金属狭缝宽度A3 为10 nm、20 nm、30 nm、40 nm、50 nm时的透射光谱。通过分析金属狭缝几何参数改变后的透射谱,可以研究边界金属狭缝几何参数与中间层金属狭缝几何参数的改变对透射谱产生的影响。

图2 不同结构参数的三层矩形狭缝阵列透射光谱
由图2 可知,图2(B_3)的透射谱从左到右出现三个相对独立的透射峰,分别是位于入射波长λ1=764 nm 的第一透射峰、λ2=1 884 nm 的第二透射峰和λ3=3 560 nm 处的第三透射峰。其中,第三透射峰的峰值最高,峰形最宽;第一透射峰的峰值最低,峰形最窄。分别改变第二层、第三层金属狭缝宽度,第一透射峰对应的入射波波长位置几乎未发生移动,第二透射峰、第三透射峰对应的入射波波长位置发生了明显移动。当第三金属狭缝宽度A3 由10 nm 增加到50 nm 时,第二透射峰的波长位置由入射波长1 975 nm 蓝移到1 845 nm 处,第三透射峰的波长位置也由入射波长4 455 nm 蓝移到入射波长3 100 nm处。当第二金属狭缝宽度A2 由10 nm 增加到50 nm时,第二透射峰的波长位置由入射波长2 620 nm蓝移到1 600 nm 处,第三透射峰的波长位置由入射波长3 210 nm 红移到3 675 nm 处。由此可知,改变金属狭缝宽度A2、A3,对第二透射峰和第三透射峰的波长位置影响并不相同。A2 的改变使第二共振峰波长位置明显移动,A3 的改变使第三共振峰波长位置明显移动,且随着两透射峰波长的位置间距增大,两峰间的波谷强度会逐渐降低。
为研究透射峰的形成机制,需要分析透射年波长位置。图2 所示的透射峰波长位置对应的电场分量Ey、分量Ex和磁场分量Hz的空间分布如图3所示。

图3 不同入射波长时法向电场分量Ey、切向电场分量Ex和电磁分量Hz分布
由边界条件n·E=σ/ε(0其中,σ为表面电荷密度)可知,在法线方向n=ny,可通过 |Ey|来推算出表面电荷的数量[19]。由入射波长λ1= 764 nm 的电、磁场分量分布图可知,狭缝的尖角处与狭缝内均分布着表面电荷,由于边缘效应,在狭缝边缘会产生累积电荷,在狭缝左右边缘表现为电偶极子。每个金属狭缝进出端的表面电荷电性相同,在狭缝间分布的表面电荷与狭缝两端的电偶极子电性相反。Hz在空气层中分布较少,磁场能量大多集中在金属表面或金属狭缝中。偶极子与狭缝内电性相反的表面电荷会相互作用,在狭缝内沿y方向形成驻波共振模式的切向电场Ex,从而引起狭缝内金属表面的等离子激元耦合。切向局域电场在狭缝两端,相邻两狭缝之间出现较小的驻波共振。
平面内表面等离子共振波长的表达见式(2)。
式中:m为所描述的光栅矢量阶数;p为狭缝阵列周期;εd和εm分别为电介质与金属的介电常数;为有效折射率[20]。由此可以看出,表面等离子共振波长与光栅有效折射率、狭缝阵列周期有关。保持结构周期性不变,第一个共振峰波长的位置移动较小,可将第一个共振峰归为表面等离子共振。
由图3 可知,Ey主要集中在狭缝的入射端和出射端,两端口同侧的表面电荷电性相反,而狭缝中只有少量电荷。金属狭缝、金属表面和两金属层间的空气层中分布着较强的磁场。Ex为波节局域在狭缝中间,在波长为λ2的图中,第一层狭缝内为负,第二层狭缝内为正,第三层狭缝内为负;在波长为λ3的图中,第一层狭缝内为负,第三层狭缝内为正。该共振模式与狭缝形状有关。其中,每一层金属膜的狭缝可看作两侧带有金属壁的截断波导形成的谐振腔。狭缝的几何参数改变对共振峰波长位置移动的影响较大。因此,将波长λ2、λ3的共振峰归因于局域波导共振。
由图2可知,金属狭缝宽度A3和金属层厚度H3的改变对两峰波长位置移动产生的影响不同,对λ2处共振峰位置的影响较弱,对λ3处共振峰位置的影响明显。由图3 可知,第二金属狭缝两端分布着较多表面电荷,第一、第三金属狭缝的表面电荷分布较少。切向电场分量Ex的能量主要集中在第二金属狭缝,即该共振波长的谐振腔主要为第二金属狭缝,而改变A3和H3对谐振腔的影响较小。由图3可知,在波长为3 560 nm的电磁场分量分布图中,第一、第三金属狭缝两端分布的电荷较多,两金属狭缝对称位置处的表面电荷电性相反,中间金属狭缝两端及周围几乎没有电荷。切向电场分量Ex的能量主要集中在上、下层金属狭缝中,两金属狭缝中Ex的电性相反。该透射峰主要由第一、第三谐振腔耦合而成,所以改变第一、第三谐振腔的结构参数对共振波长有明显影响。由于表面电荷和电场能量的分布不同,导致边界金属狭缝几何参数的变化对两局域波导共振峰有不同的调制作用。
2.1 表面等离子共振峰的分离
为研究光栅结构参数的改变对透射谱产生的影响,需要改变金属狭缝宽度和金属层厚度,得到的透射谱如图4 所示。不同金属狭缝宽度(A2=50 nm、40 nm、30 nm、20 nm、10 nm)的透射光谱如图4(a)所示,不同金属层厚度(H2=100 nm、150 nm、200 nm、250 nm、300 nm)的透射光谱如图4(b)所示。通过改变金属狭缝宽度A2和厚度H2,透射峰会出现明显的分裂现象。当A2 从50 nm 减小到10 nm 时,副峰位置的波长由1 350 nm蓝移到638 nm处;当H2从100 nm增加到300 nm时,副峰位置由波长988 nm蓝移到502 nm处。同等共振波长的位移距离,红移的副峰强度要高于蓝移的副峰强度,红移的主峰强度要高于蓝移的主峰强度。同一位移方向,随着主峰与副峰距离增大,主峰强度和附峰强度均明显降低。
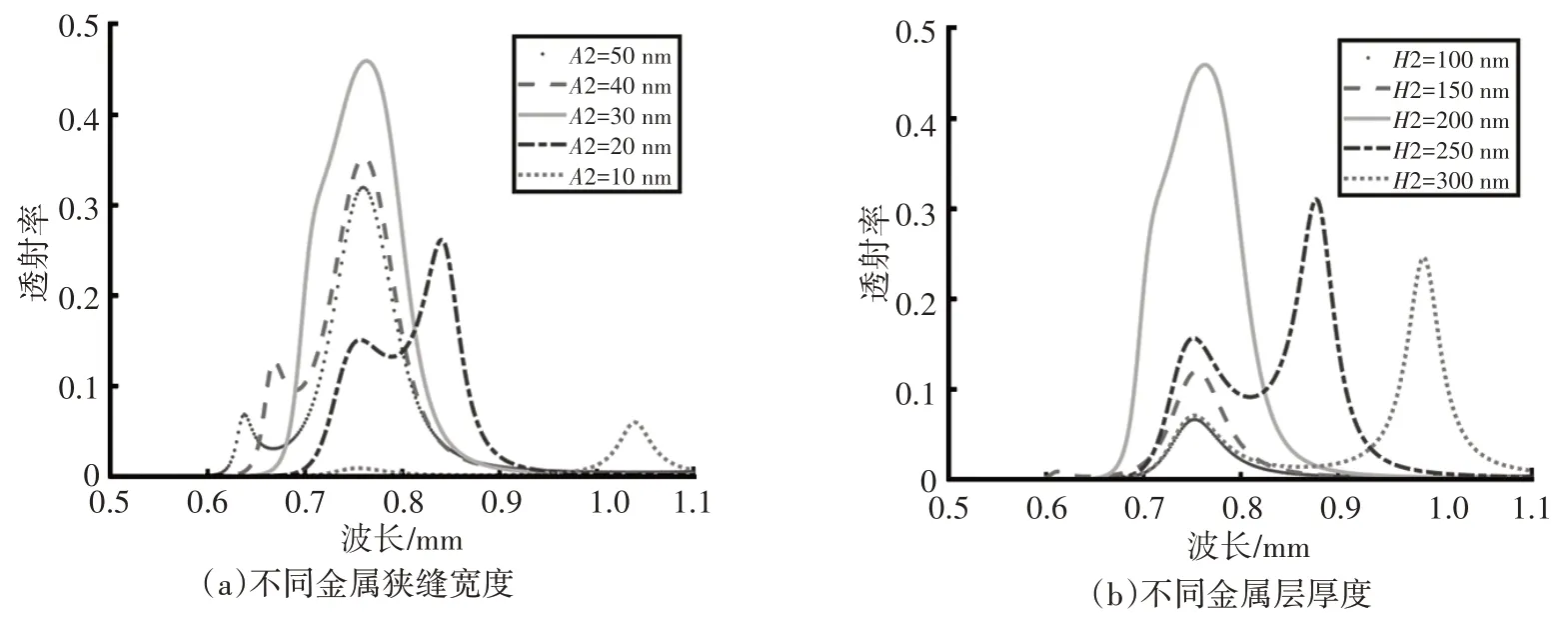
图4 不同光栅结构参数的透射光谱
为揭示λ2处透射峰分裂的物理机制,保持其他条件不变,分别只改变金属狭缝宽度A2(50 nm,40 nm,30 nm,20 nm,10 nm)、金属薄层厚度H2(100 nm,150 nm,200 nm,250 nm,300 nm),得到不同金属狭缝宽度A2、不同金属层厚度H2 下共振峰波长与分裂峰波长入射下的电场分量分布,如图5 所示。

图5 不同入射波长下的电场分量Ex分布
在三层矩形狭缝阵列中,不同金属狭缝宽度A2、金属层厚度H2与分裂波长的关系如图6所示。
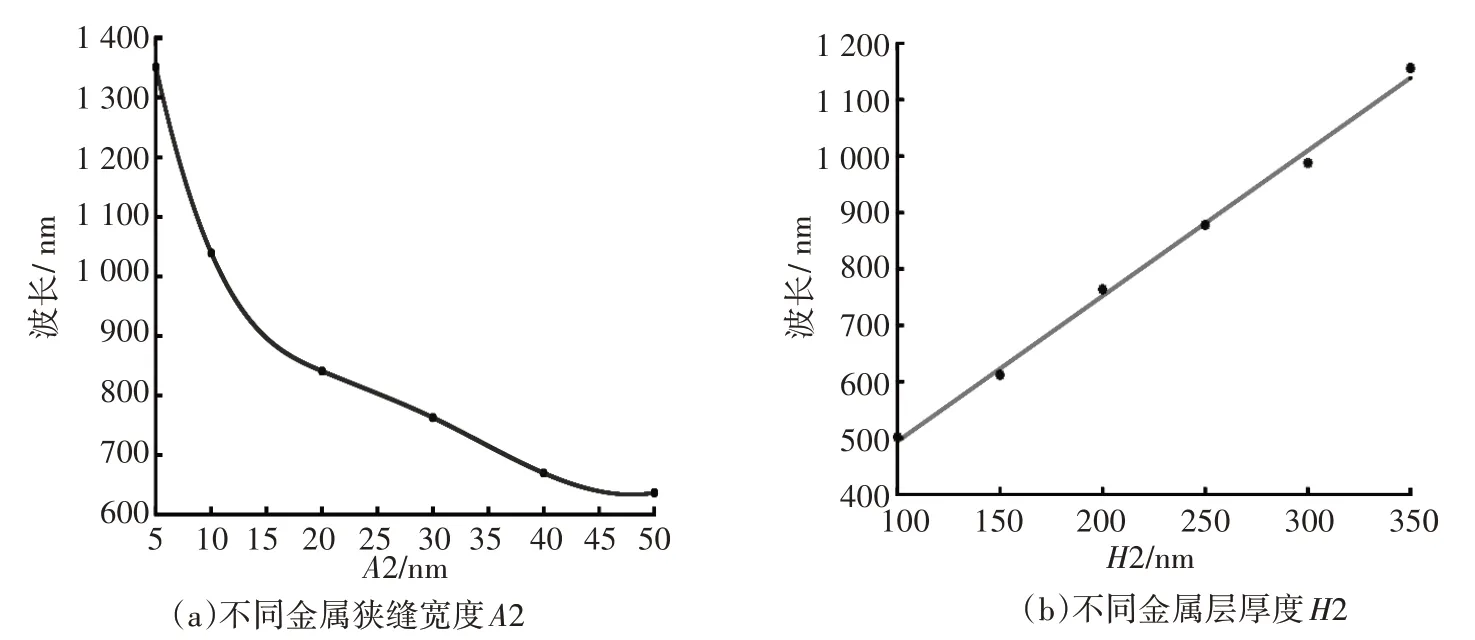
图6 不同金属狭缝宽度A2、金属层厚度H2与分裂波长关系
由图5 可知,电场分量Ex在每个金属狭缝之间分段分布,正负电场交替分布。在(A11~A15)和(H11~H15)中,正极电场主要集中分布在第一金属狭缝中,第二金属狭缝中的正极电场逐渐变为负极电场。在(A21~A25)和(H21~H25)中,电场分量Ex主要集中在第二金属狭缝中,且电场方向逐渐发生反转。电场分量Ex的分布发生变化,表明金属狭缝变化会导致电磁波的耦合位置发生变化。当各层中的金属狭缝几何参数不同时,激发局域波导共振条件的入射波长也不相同。用空间传输波中沿狭缝通道的干涉相长来描述局域波导共振模,法布里-泊罗共振条件见式(3)[21]。
式中:k0为入射光波矢;n为透射阶数取整;ρ为基本模反射系数;l为狭缝长度;neff为狭缝中传输基本布洛赫模的有效折射率。狭缝两壁上电荷密度的耦合随狭缝宽度变窄而增长[22]。由FP 共振条件可知,共振波长与狭缝宽度成反比例关系,与狭缝长度成正比例关系。图6 给出的表面等离子共振峰的分裂峰波长与金属狭缝宽度及金属层厚度的变化关系,与FP 共振条件类似,即随着几何参数变化,表面等离子共振峰下分裂峰波长位置发生变化。当A2=30 nm、H2=200 nm 时,共振峰主峰强度明显增强是由表面等离子模和FP 模耦合增强造成的。该结果对金属狭缝光学器件的透射增强具有一定指导意义。
2.2 局域波导共振峰的合并与分离
在图2(a)中,第二金属狭缝宽度A2 从50 nm 减小到10 nm,第二透射峰波长位置由1 600 nm蓝移至2 620 nm处,第三透射峰波长位置由2 675 nm红移至3 210 nm 处。第二透射峰波长位置红移与第三透射峰波长位置蓝移,使两峰波长位置的间距缩短,两峰间的波谷强度逐渐增加。金属狭缝A2 宽度变窄会导致第二透射峰红移,与法布里-泊罗共振条件相悖。为分析图2(a)中出现的第二透射峰波长位置随狭缝宽度A2 减小而红移,且有两局域波导共振峰有合并趋势这一反常现象,需要在保证其他几何参数不变的前提下,设定A2+A3=60 nm,透射谱如图7所示。由图7 可知,随着A2 的减小和A3 的增加,λ3处透射峰发生红移和λ4处透射峰发生蓝移,两峰间距逐渐减小,波谷升高,最终合并为一个峰。当A2小于A3时,两峰间距将会缩短,波谷升高;当A2小于A3,且A2 与A3 差值增大时,两共振峰将会合并。双层矩形狭缝阵列的透射谱中有一个FP 共振峰,三层矩形狭缝阵列的透射谱在一定条件下可实现单FP共振峰。由图7 可知,双层与三层矩形狭缝阵列在A2 相同时,共振峰波长位置几乎相同,三层矩形狭缝阵列的共振峰强度要高于双层。

图7 几何参数对透射谱的影响
以图7(b)和7(d)中各共振峰波长的入射光栅来绘制电场分量,如图8 所示。双层矩形狭缝阵列与三层矩形狭缝阵列第一、第二金属层周围的表面电荷分布和电场分量Ex分布相似,第三金属狭缝区域分布的电场分量极少。狭缝阵列中FP 模式的共振波长[23]表示见式(4)。
式中:k= 2nπ/λ为入射波波数;LFP为谐振腔的长度;θ为从狭缝末端反射到前端的相位差;N为整数。
第二共振峰的耦合位置主要位于第二金属狭缝中,第三共振峰的耦合位置位于第一、第三金属狭缝中,由此可知,第二金属狭缝的居于波导共振波长小于第一、第三金属狭缝的局域波导共振波长。随着第二金属狭缝宽度减小与第三金属狭缝宽度增大,第二金属狭缝中谐振腔的共振波长会逐渐增大,第三金属狭缝谐振腔的共振波长会逐渐减小。当第三金属狭缝共振波长与第二金属狭缝共振波长逐渐接近时,第二金属狭缝会逐渐替代第三金属狭缝发挥作用。以共振波长入射的TM波为例,电磁场在结构中的耦合位置主要在第一、第二金属狭缝,第三金属狭缝的耦合作用由第二金属狭缝所替代。
3 结语
通过改变各金属层的厚度、狭缝宽度及空气层厚度,本研究利用有限元(FEM)法来研究不同位置金属狭缝几何参数的改变对光通过多层膜传输行为的影响。与单层和双层矩形狭缝阵列相比,金属层具有更多的可调控几何参数,能增加光调控的自由度。研究结果表明,不同共振峰波长的电磁场分量分布不同,改变不同位置金属狭缝的几何参数,会对共振峰的位置、强度、峰形产生不同影响。调节金属狭缝的几何参数,会引起表面等离子共振峰的分裂,分裂峰波长位置的规律性移动和主峰波长位置几乎不变,与FP-SPP 耦合模理论相符,表面等离激元模与FP 模的耦合将提高共振峰强度。金属狭缝宽度的改变与空气间隙的改变会引起局域波导共振峰的合并,可能是由第二金属狭缝与第三金属狭缝的局域波导共振波长接近,第三金属狭缝的耦合作用缺失而导致的。本研究所得结果对金属狭缝光学器件设计具有一定指导意义。

