建筑单体化模型精度检测方法研究*

高崇民,达多双,刘云波

(浙江省测绘科学技术研究院,浙江 杭州 310030)

0 引言

近年来,随着城市治理“科学化、精细化、智能化”的要求和数字经济的发展,对智慧城市的建设提出了更高的要求。城市三维模型作为智慧城市的重要载体,其建设和利用能够促进智慧城市的发展。

倾斜摄影方法是目前获取城市三维模型的主要技术手段,要达到高精度、可量测、部件化的三维模型数据要求,可基于倾斜摄影三维模型数据提取建筑单体化模型。将三维模型进行单体化处理是三维数据进一步应用的重要步骤,因此基于倾斜摄影三维模型提取的建筑单体化模型质量必须满足后续应用的要求。

本文针对建筑单体化模型精度检测问题展开一系列的研究与实验,旨在高效率地完成单体化模型质量评估工作,减轻人工检查工作负担,并确保建筑单体化模型质量得到有效控制。

1 倾斜摄影三维模型与建筑单体化模型的特点

1.1 倾斜摄影三维模型

倾斜摄影三维模型也可以称作实景三维模型,是通过在低空以不同角度对地面进行摄影测量获取的多视角影像来生产的三维模型,由连续的不规则三角网组成,即Mesh网格模型。

倾斜摄影自动化建模的过程可以简单描述为:先经过多视影像匹配、连接点提取、空三加密、抽取特征点等一系列复杂的运算得到带有高程的稠密的点云数据,通过抽稀,构建一张连续的TIN三角网构成白模,最后把拍摄的高分影像自动贴到三角网上,最终得到城市实景三维模型。相较于传统三维建模方法,倾斜摄影技术大大提高了三维重建的效率,降低了人工和时间成本,实景三维模型也更加准确地还原了地物的真实面貌[1]。但以 TIN 网模型将整个场景各类地物要素“粘连”在一起,形成“一张皮”,各类要素并没有实现对象化,而是所有地物要素模型为统一的结构模型[2]。这种结构模型不容易被计算机识别、理解和分析,难以进行自动地物统计分类、信息提取,无法智能管理,这对倾斜摄影三维成果的深度利用和价值挖掘形成了一定程度的阻碍。

1.2 建筑单体化模型

本文研究的建筑单体化模型是以倾斜摄影三维模型为基础进行的模型重建成果。首先借助集精细化单体建模及Mesh网格模型修饰于一体的倾斜摄影三维建模软件(如DP-Modeler、清华山维EPS倾斜摄影三维测图系统等),通过特有的摄影测量处理算法,引入倾斜影像处理软件(ContextCapture、Photomesh、街景工厂、DPsmart等)生成的空三及实景三维模型等多数据源成果,以空地一体化作业模式,根据建筑物外表面特征结构,人工采集建筑三维矢量轮廓线,按照目标实际细节程度,对建筑矢量轮廓进行拉伸操作和编辑,制作建筑单体白模,同时利用倾斜影像对构建好的单体化白模进行纹理映射,影像遮挡区域利用实地采集照片的方式进行贴图补充。最后参照已有基础库文件资料,经过内业判定,外业调查补充的方式完成单体化模型的属性录入。

建筑单体化模型作为倾斜摄影三维模型的模型重建地理信息产品,在后期的三维数据管理过程中可单独选中实体对象,同时可以进行属性查询、统计分析等操作。

2 建筑单体化模型精度检测算法设计

建筑单体化模型作为地理信息产品,具有地理位置信息,因此建筑单体化模型的位置精度应满足相应产品标准所规定的精度要求。本文讨论的建筑单体化模型精度主要是指相对位置精度。

在人工采集建筑三维矢量轮廓线的过程中,由于Mesh网格模型有拉花、变形、遮蔽等现象,造成三维矢量轮廓线不能准确贴合Mesh模型。

为保证建筑单体化模型能够准确反映建筑物外表面特征结构,三维矢量轮廓线与Mesh模型之间的相对位置必须保持在一定的限差范围以内。对建筑单体化模型与Mesh模型的相对位置精度进行计算,能为评估分析单体化模型的相对精度提供数据支持。

由于单体化模型的矢量轮廓线角点数据量较大,依靠人工交互采集角点坐标,将会产生大量人力和时间成本,同时可能会存在一定的人为误差。因此,本文提出一种自动化的方法,通过选取建筑物单体化模型的角点位置与Mesh模型之间进行比对,可快速自动统计单体化模型与Mesh模型的相对位置精度。

为了减少软件计算量,提高检测速度,需要将建筑单体化模型同位置的Mesh模型从整个区块大Mesh模型中分离出来。为切割局部的Mesh模型,首先将需检测精度的建筑单体化模型的范围线提取出来,以此范围线切割区块Mesh模型,获得单体化模型同位置、局部的Mesh模型,利用算法批量自动搜查单体化模型角点附近与之最近Mesh三角网的网格节点,再计算两者之间的差值,最终实现单体化模型相对位置精度的自动化匹配输出。

具体方法如下:

1)获取建筑单体化模型的凸多面体V0;

2)将凸多面体V0投影于XOY平面上获得二维点集Pt,再求出点集Pt的凸多边形PG1;

3)将凸多边形PG1的AABB(Axis Aligned Bounding Box,轴对齐-边界盒)与Mesh网格面片求交运算,获得与AABB范围内的三角面片集Ti;

4)将凸多面体V0的角点坐标与三角面片集Ti中三角面片角点的同名点自动进行比对获得相对差值,进而计算出相对精度。

2.1 获取建筑单体化模型的凸多面体

建筑单体化模型是由三维矢量轮廓线组成,可先将三维矢量轮廓线的角点提取出来组成角点集P,再基于角点集P计算建筑单体化三维模型的空间凸多面体,即三维凸包。三维凸包是指在空间几何上,包含一系列已知顶点的最小凸多面体[3]。计算三维凸包的算法有很多种成熟的算法,包括随机增量法、Graham扫描法、Jarvis步进法、分治法和快速算法(Quickhull算法)等[4]。

本研究采用的是快速三维凸包生成算法获取三维凸包。算法步骤如下:

1)初始化一个四面体,选取点集P中4个最远点,即由(X,Y,Z)坐标轴上最大值或者最小值的4个点组成四面体V′。

2)循环迭代V′的每一个面Fj(j=1,2,…,n),采用矢量点积的方式判断未分配点Pi(Pi∈P,i=1,2,…,n)是在Fj的上方还是下方,计算公式为:

(1)

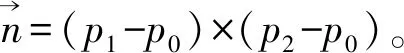
若S<0,说明Pi在Fj下方,不作操作;若S>0,说明Pi在Fj上方,则将Pi加入点集Pipg。

经过对所有未分配点进行点积计算后获得点集Pipg,然后再计算Pipg中与Fj的最远点,得到点Pimax。

3)若Pimax只面对Fj,则将Fj删除,然后添加3个面(1 3Pimax,2 3Pimax,1Pimax2)获得新的凸多面体V′(如图1)。

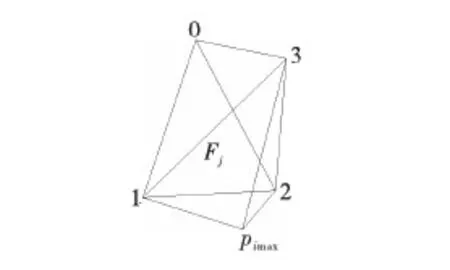
图1 获得新的凸多面体Fig.1 Obtained new convex polyhedron

若Pimax同时对Fj及其有公共边的邻面Fj+1可见,则以公共边为基础,进行迭代计算,依次去掉可见面,添加包含Pimax的新面,获得新的凸多面体V′。 如图2所示。

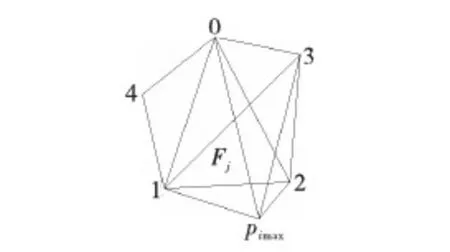
图2 迭代计算后获得新的凸多面体Fig.2 Obtained new convex polyhedron after iterative calculation

4)重复步骤3),直至无未分配点Pi,获得最终的凸多面体V。

2.2 求取凸多面体在XOY平面上的投影多边形

提取凸多面体V中的所有角点,形成点集Pv(x,y,z),点集Pv中的坐标点Pi位于三维空间直角坐标系中,点Pi在X轴、Y轴、Z轴上的投影距离分别为xi、yi、zi。为了方便后续的计算,可直接选取XOY平面作为投影面,那么Pi在XOY平面上的坐标为(xi′,yi′),同理可得二维点集Pt(x′,y′)。

因下一步将使用建筑单体化模型范围线切割区块大Mesh模型,需要凸多边形求其AABB,并进行求交检测。所以,本研究根据二维点集Pt采用快速二维凸包生成算法来获得二维凸多边形。

首先找出Pt的两个极点,即横坐标方向上的最大点P1和最小点P2,这两个点必定是凸包上的点,将这两个点加入凸包。枚举点集中所有点判断与线段P1P2的关系,利用向量叉乘判断点在线段P1P2的左边还是右边,向量叉乘的值除2后是向量所围成的三角形的面积,面积越大则此点离线段P1P2越远,求出最远点即是凸包点。通过正向遍历和逆向遍历即可得到二维凸多边形PG1。

2.3 利用凸多边形切割Mesh网格模型

利用凸多边形对Mesh网格模型进行切割,主要的工作是判断切割多边形与哪些三角面片发生相交,然后将多边形内的三角面片提取出来。整个区块大Mesh模型中的三角面片个数非常多,切割多边形需要与每个三角面片进行求交运算,这将耗费大量的时间,效率不高。

倾斜摄影三维模型是真实世界的数字化产物,其地物模型的绝大多数立面近似垂直于地面等特点,利用这些特点则可以将Mesh网格模型中三角面片直接投影到XOY平面上,而二维三角面片相对于二维凸多边形PG1的位置不发生改变。本研究采用AABB碰撞检测算法在二维空间中进行求交检测,将大大提高工作效率。

AABB是3个轴向量都分别平行于世界坐标轴的立方体结构[5],二维场景中的AABB则只取平行与X、Y轴的轴向量,表现形式为平面四边形,即用四边形包围凸多边形(或线段),可以通过二维空间坐标上的4个坐标值进行描绘,计算公式如下:

S{(X,Y)|Xmin≤X≤Xmax,Ymin≤Y≤Ymax|}

(2)

式中:Xmin、Xmax、Ymin、Ymax表示凸多边形(或线段)在坐标空间中顶点的最小值和最大值。

以二维凸多边形PG1中拐点的Xmin、Xmax、Ymin、Ymax构造为AABB-S0,以投影到XOY平面上的三角面片角点的Xmin、Xmax、Ymin、Ymax构造为AABB-Si(i为Mesh模型中三角面片的序号)。二维凸多边形PG1及其AABB叠加示意图如图3所示。

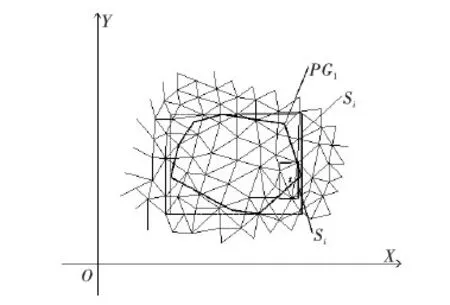
图3 二维凸多边形PG1及其AABB叠加示意图Fig.3 Schematic diagram of 2D convex polygon PG1 and its AABB superposition

在AABB碰撞检测时,需遍历验证Si与S0是否满足如下条件:

1)Si的Y轴方向最小值大于S0的Y轴方向最大值;

2)Si的X轴方向最小值大于S0的X轴方向最大值;

3)S0的Y轴方向最小值大于Si的Y轴方向最大值;

4)S0的X轴方向最小值大于Si的X轴方向最大值。

若满足上述条件,则证明Si与S并未发生重叠。反之,则证明物体Si与S有重叠,将Si包裹下的三角面片i记录在三角面片集Ti中。

至此,与建筑单体化模型同位置、局部的Mesh模型已被提取至三角面片集Ti中。

2.4 计算建筑单体化模型的相对位置精度

将建筑单体化模型同位置、局部Mesh模型的三角面片集Ti中角点提取至角点集PT。遍历凸多面体V角点集Pv中的角点与角点集PT匹配,查找两者之间最近的点对。在自动查找同名点过程中,由于数据量较大,需要为角点集PT建立一个的高效空间索引来解决。本研究采用KD树索引的方式在三维空间中将角点集PT中的点划分到具体的特定空间,在每个特定空间内进行相关搜素,KD树每个节点存储的是三维点数据。在KD树中搜素与查询点距离最近的数据点计算公式为:

(3)

查找结束后,获得最近点对集Pd,点对的点之间的距离即为建筑单体化模型与Mesh模型的相对差值。计算建筑单体化模型相对位置精度公式为:

(4)

式中:M为中误差;n为 点对总数;Δi为相对差值。其中,平面和高程相对位置精度计算公式统一使用式(4)。

3 算法实现

为了验证本方法的有效性,开发了一套建筑单体化模型质量检查软件。在此软件中根据研究内容进行了具体算法实现。

遍历建筑单体化模型集,获取单体化模型的凸多面体V0,依次将V0的平面范围线与Mesh网格模型切割获取局部Mesh网格模型,通过单体化模型与局部Mesh网格模型的位置比对,获得了单体化模型相对位置精度。具体实现步骤如下:

1)输入:

建筑单体化模型凸多面体V0

Mesh网格面片集合meshPieces

2)准备输出:

角点误差列表pointErrors

3)函数:项目到XY平面

函数 projectToXY(多面体V,点集P):

初始化点集P

对V的每个角点A:

将A的x,y坐标添加到P中

返回P

4)调用projectToXY投影V0到XY平面

Pt=projectToXY(V0)

5)函数:计算凸包

函数 convexHull(点集P,多边形G):

使用Gift Wrapping等算法计算P的凸包

返回凸包多边形G

6)调用convexHull求Pt的凸包

PG1=convexHull(Pt)

7)函数:计算AABB

函数 calculateAABB(多边形P):

初始化AABB为Null

对P的每个顶点V:

更新AABB包含V

返回AABB

8)调用calculateAABB计算PG1的AABB

AABB=calculateAABB(PG1)

9)初始化三角面片集合Ti

Ti=空集合

10)遍历Mesh面片集合meshPieces:

对每个面片Pin meshPieces:

IFP与AABB相交:

将P添加到Ti中

11)初始化误差列表pointErrors

pointErrors=空列表

12)对V0每个角点V:

对Ti每个面片T:

计算V与T三角形每个角点的距离d

记录最小距离minDist

将minDist添加到pointErrors中

13)返回点误差列表pointErrors。

4 实例测试

在实际项目应用中,为了测试此方法进行建筑单体化模型质量检查精度的工作效率,针对某地区基于倾斜摄影三维模型提取建筑单体化模型项目的精度检测工作,选取8幢多层建筑的单体化模型,通过软件检查与人工交互检查两种方法测试相对位置精度检测的工作效率。对比结果见表1。

表1 软件与人工交互检测效率对比

通过软件检查获得的平面和高程精度结果如表2、3所示。

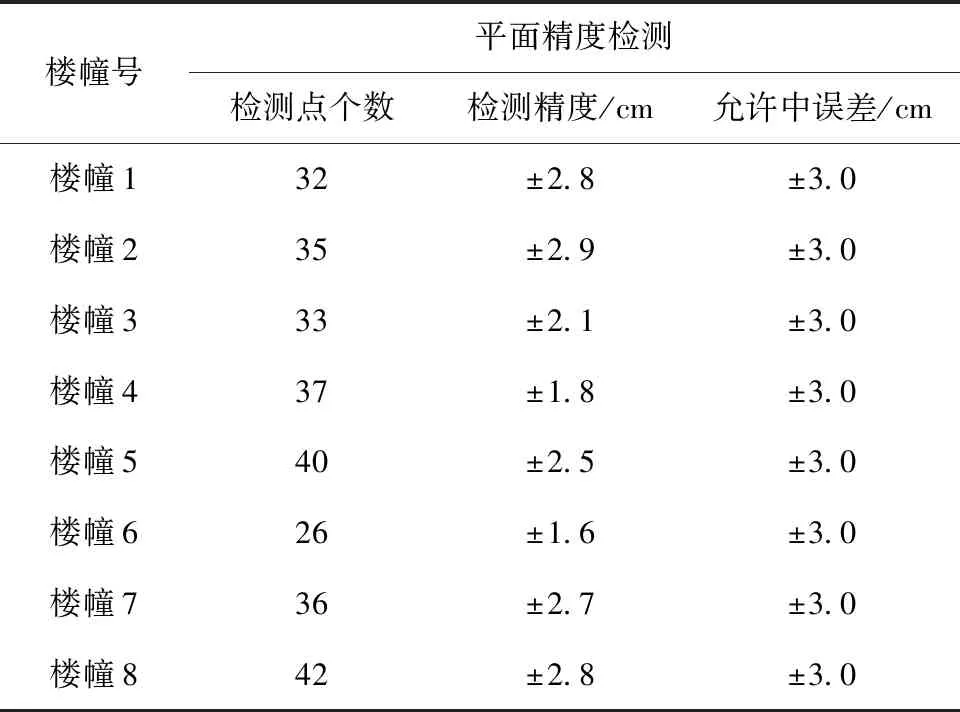
表2 平面精度检测结果表

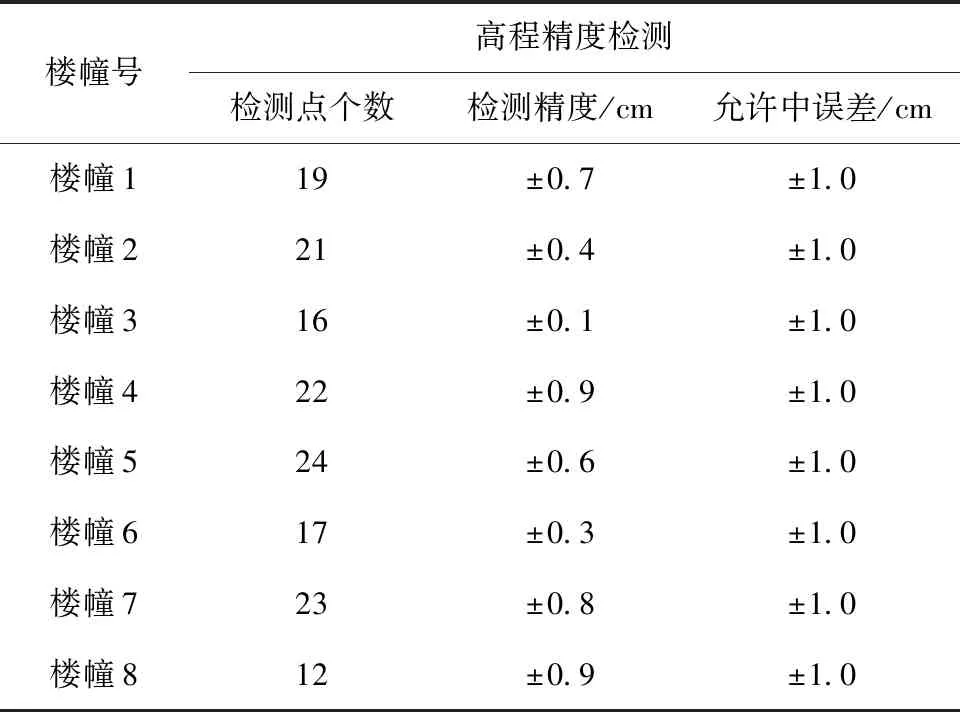
表3 高程精度检测结果表

测试结果表明,利用本文提出的自动化方法可以快速地检测建筑单体化模型的相对位置精度,并且具有一定的可靠性。同时,这种方法可以减轻人工检查的工作负担,提高工作效率,为建筑单体化模型的质量控制提供了一种可行的技术手段。

5 结束语

本文研究了基于倾斜摄影的建筑单体化模型的相对位置精度检测方法,并提出了一种高效的检测方法。该方法通过切割与建筑单体化模型同位置的局部Mesh模型以降低精度检测的计算量,同时在自动对比同名点时,为Mesh模型的角点集建立了KD树索引,加快搜索效率,经过了一系列的算法优化,本方法在精度检测方面具有较高的工作效率。实验结果表明,该方法能够高

效地检测建筑单体化模型的相对位置精度,与传统人工交互比对的检测方法相比,具有更高的效率和可靠性。