基于CatBoost算法的SAP混凝土抗压强度预测

李 宁，杨镇华，马伟中，李 昊，王行行

（1.甘肃省公路交通建设集团有限公司，甘肃 兰州 730030；2.兰州交通大学土木工程学院，甘肃 兰州 730070；3.甘肃省公路发展集团有限公司甘肃省路网监测重点实验室）

0 引言

混凝土的早期开裂现象是影响混凝土质量的重要原因之一，其中自收缩又是开裂的主要原因。近年来，混凝土领域采用内养护剂作为一种混凝土养护新措施得到了关注与应用。内养护剂作为预先吸水并在特定的条件下释放水分的一种均匀分散在混凝土内部的养护材料，具有高吸水性、高保水性和高稳定性的特点。其中，高吸水树脂（SAP）是一种具有很高吸水倍率的高分子聚合物材料，其内部的空间网络结构能够吸收并且存储水分，在混凝土内部起到蓄水池的作用，当与外部溶液的渗透压发生变化时会释放出水分改善混凝土内部相对湿度，从而达到内养护的作用。但是，部分研究表明，掺加预吸水内养护剂的混凝土各龄期强度都有不同程度的减小，且内养护剂掺量越高，强度降低越明显。因此，全面了解SAP 抗压强度变化规律，科学预测SAP的抗压强度，对于SAP的应用具有重要借鉴意义。

近年来，采用机器学习回归算法来预测混凝土抗压强度的方式已受到国内外学者的广泛关注。其中，研究人员通常会选取人工神经网络的算法，对混凝土强度进行预测分析[1]。陈洪根等人[2]构建了以粉煤灰混凝土的七个影响因素为输入变量的强度预测模型，通过模型训练和测试结果的相关系数对比证实了基于BP神经网络的粉煤灰混凝土抗压强度预测方法的可行性。赵明亮等人[3]以混凝土公司总结出的原材料表波动因素和配合比设计为输入层，通过BP 神经网络模型预测中低混凝土7 d 和28 d 抗压强度，发现该方法具有很强的非线性映射能力，其预测的强度结果精度可达0.95以上。陈庆等人[4]引入遗传算法（GA）优化了UHPC抗压强度预测的BP 神经网络模型的初始权值和阈值，通过模拟训练UHPC 抗压强度预测GA-BP 神经网络，建立了基于不同性能需求的配合比设计方法。虽然BP神经网络在混凝土强度预测方面表现优异，但BP 神经网络仍存在训练过程收敛速度较慢、鲁棒性较差、容易陷入局部最优解而不是全局最优解等一系列问题[5]。

本文建立了一个基于机器学习的CatBoost 回归算法[6]的SAP混凝土抗压强度预测模型，以水胶比、SAP掺量、预吸水倍数和养护龄期作为预测模型的输入指标，以混凝土的抗压强度为研究对象，通过SAP 混凝土制备及其强度检测构建了156份数据样本，与常见的机器学习算法（包括LightGBM 算法和XGBoost 算法）进行比较，利用各指标对抗压强度的影响验证该模型预测效果。研究结果可对SAP 混凝土抗压强度精确预测和顺利施工提供一定指导作用。

1 原材料及试验方法

1.1 原材料

水泥选用P·O42.5 级普通硅酸盐水泥，具体性能指标见表1。粉煤灰选用Ⅱ级粉煤灰，主要化学成分见表2。

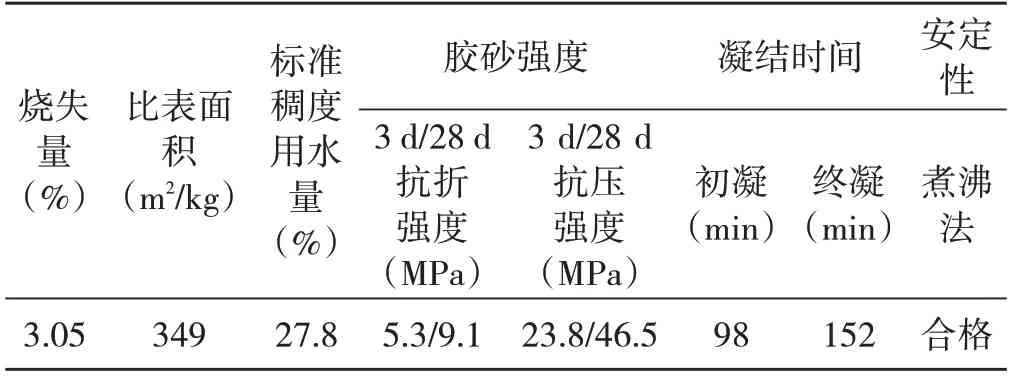
表1 水泥的性能指标

表2 粉煤灰化学成分

细骨料采用级配良好的水洗河砂，细度模数2.45，表观密度2646.5 kg/m3，含泥量0.66%。各项指标符合《建设用砂》（GB/T 14684—2022）规定。

粗骨料选用反击破碎碎石，粒径5 mm～31.5 mm，连续级配，表面比较粗糙、质地坚硬，表观密度2670.8 kg/m3，压碎指标10.3%。各项指标符合《建设用碎石、卵石》（GB/T 14685—2022）规定。

外加剂为聚羧酸系高性能减水剂，减水率为27%。高吸水树脂（SAP）为实验室自制聚丙烯酸-丙烯酰胺。

水符合《生活饮用水卫生标准》（GB 5749—2006）的规定，拌和用水所含物质不能对混凝土试验结果造成影响，且不能具有腐蚀性。

SAP选用自制的SAP进行后续试验。

1.2 混凝土配合比设计

本文主要研究SAP 对混凝土力学性能、收缩性能、抗裂性能及微观结构的影响。水胶比采用0.30、0.35和0.38三种，混凝土配合比根据《普通混凝土配合比设计规程》（JGJ 55—2011）的相关要求计算得出，具体见表3。

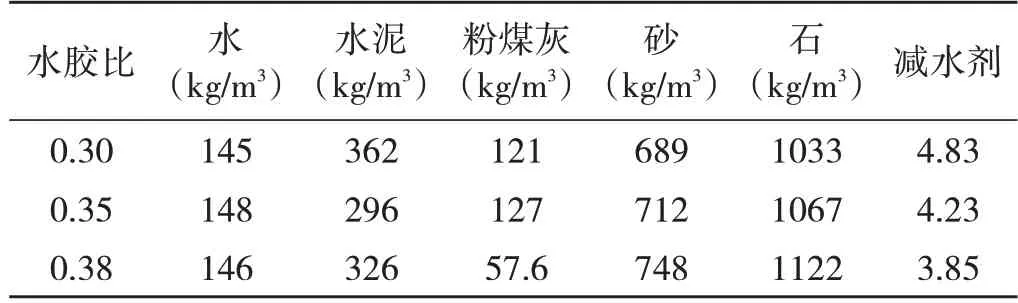
表3 混凝土配合比

1.3 试验方法

按照《普通混凝土力学性能试验方法标准》（GB/T 50081—2016）中的要求对混凝土抗压强度进行测试，以水胶比、SAP 掺量和预吸水倍数为变量，制备混凝土样品并测定其3 d、7 d、14 d、28 d的抗压强度。

2 理论与方法

2.1 CatBoost算法

CatBoost算法是由PROKHORENKOVA L 等[7]于2017年提出的基于梯度提升决策树的算法框架。CatBoost算法是梯度提升机器学习的算法，梯度提升是一种迭代算法，通常基于决策树。先建立一个基础模型，该模型具有较高的误差，考虑到该模型的误差，再建立另一个模型，通过这种方式，经过数千次迭代后，误差被最小化。该算法具有更高的准确性和泛化能力，能够高效合理地处理类别型特征、梯度偏差、预测偏移等问题，其决策树结构使模型能够可视化，根据输入层数据的特征重要性评估增强模型的可解释性，且过拟合的发生概率也显著降低[8，9]。LENKA S R 等[10]采用五种基础模型与CatBoost等十四个集成模型对比数据集的性能，比较结果表明在准确度等五项指标（均方误差、均方根误差、平均绝对误差、平均绝对百分比误差、相关系数）中CatBoost 评分显著优于其他模型。TANHA J 等[11]研究发现，CatBoost 对多类不平衡数据集的求解显示出比其他算法更好的特性。

2.2 LightGBM算法

轻量级梯度提升机（Light Gradient Boosting Machine，LightGBM）是GBDT 算法的另一种发展形式，采用叶子节点的深度限制策略，通过在当前叶子节点中寻找增益值最大的节点进行分裂，限制树的深度，从而避免过度拟合，并缩短最优深度树的搜索时间。在保持分裂次数不变的情况下，能够通过降低误差来提升精度。LightGBM 中的决策树子模型是采用按叶子分裂的方法分裂节点的，因此其计算代价比较小，也正是因为选择了这种分裂方式，需要控制树的深度和每个叶子节点的最小数据量，从而避免过拟合现象的发生。徐国天等[12]融合了XGBoost 和LightGBM 创建了双层模型的恶意软件检测方法，单独使用LightGBM 只能作为第二层模型对数据正常与否进行判断，并不能对数据进行过滤以及获取最优参数的组合。

2.3 XGBoost算法

XGBoost 算法以模型的性能与计算速度相平衡为目标函数，采用二阶泰勒展开式加快了求解速度，减少了模型的运行时间。利用正则项对模型复杂度进行控制以避免过度拟合现象发生。XGBoost 是近年来新兴的一种高效算法，能够自动利用CPU 的多线程进行并行处理，在效率及精度上都具有优势。王红爱[13]利用XGBoost 算法对旅客退票率进行了分类，并验证了算法的有效性。

3 SAP对混凝土抗压强度影响及机器学习模型分析

3.1 SAP对混凝土抗压强度的影响

抗压强度是混凝土力学性能中最重要的指标之一，是工程设计中首先要考虑的因素。本文研究了不同水胶比混凝土在不同SAP 掺量下的抗压强度，试验结果如图1所示。

图1 三种水胶比下不同SAP掺量混凝土抗压强度随龄期的变化

由图1 可知，随着养护龄期延长，混凝土抗压强度迅速增大，表明养护龄期对混凝土抗压强度有较大影响。不同水胶比条件下混凝土抗压强度增长趋势基本一致。在水胶比为0.3 的条件下，水泥混凝土抗压强度与SAP 掺量之间没有明显的规律性，但从整体上看，混凝土抗压强度随SAP 掺量增大而减小。其原因可能是由于干掺SAP 在低水胶比时，使早期参与水化反应自由水进一步减少，水化程度较小，早期产生干缩较大，在宏观上表现出强度下降。在水胶比分别为0.35 与0.38的情况下，SAP 在一定掺量下能够提高混凝土抗压强度。其原因可能在于SAP 具有“吸水—释水”的性质，反应前期SAP 吸收了一部分拌和水而形成“蓄水库”，致使较少水分参与水化反应，水化反应发展到一定阶段时，由于内部水分缺失造成其内外层存在湿度差，SAP 中存储的“蓄水库”就会开始释放水，从而使得水化反应能够持续发生。

SAP控制了混凝土水化进程，避免了混凝土内部由于水分不足导致干缩应力的出现，使混凝土宏观性能得到改善。但由于混凝土强度受各种因素（如水胶比、SAP 掺量）共同作用，很难从一般变化曲线中分析得出各种因素对其抗压强度的影响规律，以及从各个方面进行参数调节，从而达到控制混凝土抗压强度大小的目的。因此，采用机器学习算法来预测掺SAP 混凝土的强度以方便获得各个参数对于混凝土抗压强度的影响，并且得出能够根据各种影响参数对混凝土抗压强度进行合理预测的方法，从而为SAP 混凝土的实际工程应用奠定基础。

3.2 SAP抗压强度预测模型的构建

3.2.1 数据预处理和评价指标

①模型初始化。

根据输人变量和输出变量来确定模型输人层、隐藏层、输出层的节点个数,拆分对应的节点(包括特征值和边界值)并构建学习器。

②隐藏层输出计算。

③输出层输出计算。

对于任意一叶节点对应的样本,其拟合最佳输出值为：

式中,c为叶节点的输出值,结合所有叶节点的输出值即可得到所需的拟合函数,即:

式中，I{xi}为示性函数。

综上,经过第t轮迭代后，可以得到-一个强学习器，既：

④判断机器学习算法迭代是否结束。

用机器学习算法总体误差是否达到精度要求来判断，如没有达到精度要求则需返回步骤②。

3.2.2 机器学习算法的参数训练

①参数选取。

机器学习算法的训练参数来源于SAP混凝土相关实验结果,涉及四个输人参数(水胶比、SAP掺量、预吸水倍数、养护龄期)和一个输出参数(混凝土抗压强度)。

水胶比主要反映混凝土用水量与胶凝材料的用量,本文设定0.30、0.35、0.38三种水胶比;SAP掺量选择0、0.1%、0.3%和0.5%四个等级;预吸水倍数选择0、10、20、30四个等级;养护龄期(Day)设定3d、7d、14d、28 d四个阶段养护龄期。

混凝土抗压强度Fe(MPa)反映混凝土强度等级。

②参数归一化和标准化处理。

原始数据可能因为缺失值,数据类型、量纲不一致,特征值的取值范围相差较大而影响模型的精度和训练速度。因此,在确定模型参数后,将数据通过式(6)进行归一化处理,将特征数值线性映射至[0,1]区间。

但归一化方法对奇异值敏感,故可以使用标准化

处理,将特征数值映射到均值为0、方差为1的正态分布中,如式(7)所示。

式中，X*为标准化后的特征值;μ为特征值均值;σ为特征方差。

3.2.3 机器学习算法精度评价指标

通过建立统--的量化评价标准来衡量机器学习算法的预测效果,本文选择均方误差(MSE)、均方根误差(RMSE)、相关系数(R2)为具体量化指标,各指标计算公式见式(8)～式(10)。

3.2.4 模型的构建与分析

通过SAP对混凝土抗压强度影响的实验,构建SAP混凝土抗压强度数据集。通过控制不同的变量确定表4所展示的156组数据，其中随机选取109组数据用来模型训练,即作为训练集,剩余47组数据作为测试集用来验证模型的可靠性。

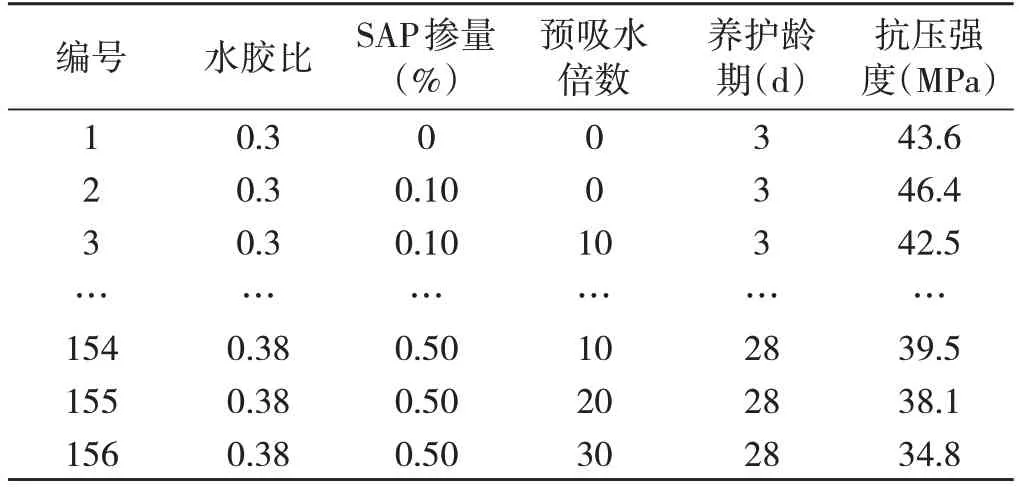
表4 混凝土配合比设计

依据抗压强度数据集对模型进行训练和模型验证，其机器学习回归算法流程图如图2所示。

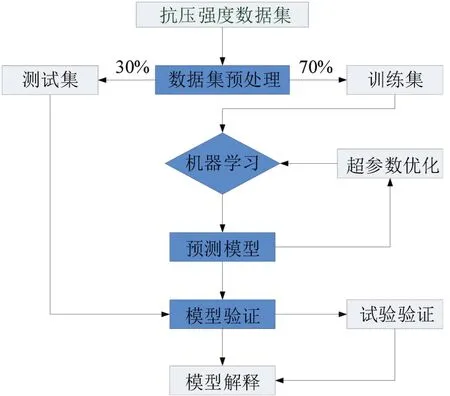
图2 机器学习流程图

在回归模型中，各种特性的重要性占比如图3 所示。从图中可以看出，水胶比所占比例最大，为55.5%，这对模型的精度影响较大；养护龄期次之，占36.0%；SAP 掺量对于预测结果影响不大，占4.7%；预吸水倍数对该模型影响最小，占比不到4%。

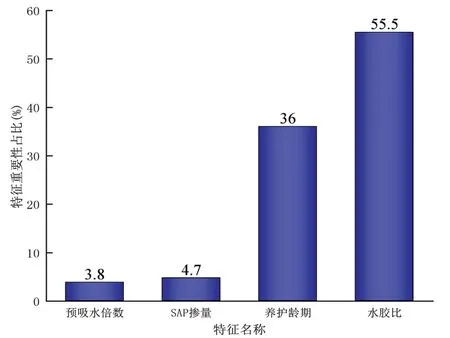
图3 模型的特征重要性占比

为了更好地度量不同模型对混凝土抗压强度的预测效果，将CatBoost模型与LightGBM 模型和XGBoost模型的抗压强度预测结果进行比对分析。表5 给出了三种机器学习算法在训练集和测试集中的具体量化指标，具体包括均方误差（MSE）、均方根误差（RMSE）和决定系数（R2）。对决定系数而言，模型的结果越接近1，模型准确度越高。其余两项指标，取值越小模型准确度越高。

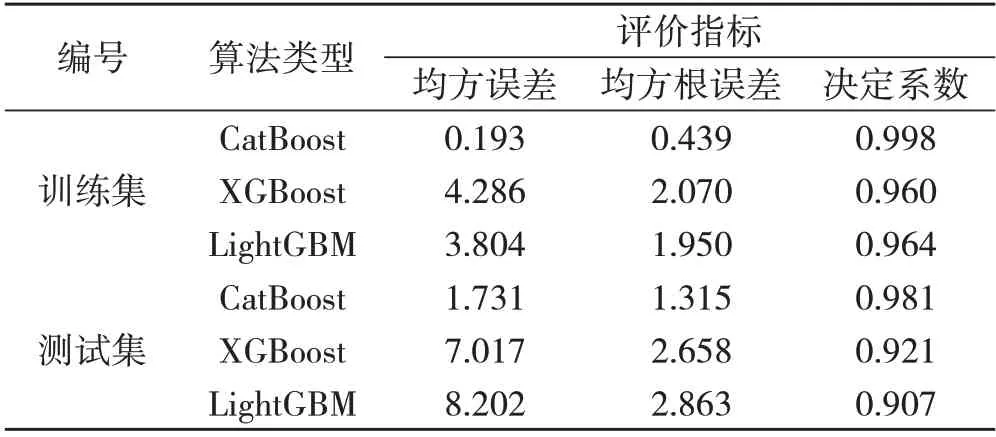
表5 模型评估结果

由表5 可以看出，无论是训练集还是测试集，三种机器学习回归算法中，CatBoost 回归算法的三项评价指标均为最优，其决定系数（R2）为0.981，XGBoost 算法次之，其决定系数（R2）为0.921，LightGBM 的性能较差，其决定系数（R2）为0.907。说明CatBoost 算法模型预测的数据与真实数据拟合程度较高，预测结果的准确性和可靠性优于XGBoost 和LightGBM 算法。此外，三种机器学习算法在训练集中的决定系数均在0.9 以上，表明输入层和输出层之间具有较强的相关性。

此外，CatBoost 模型训练集的RMSE 为0.439，决定系数为0.998，测试集的RMSE 为1.315，决定系数为0.981，可见该CatBoost 模型对混凝土抗压强度预测的泛化能力强，对掺加SAP 的混凝土抗压强度预测精准度较好。

不同模型的实测值和预测值误差分析如图4所示，散点图的中心线代表强度预测值恰好等于实际值，小方块为数据集中的样本点。

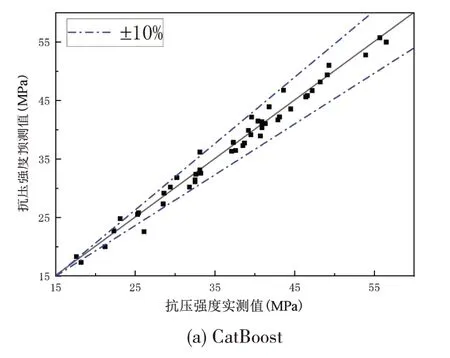
图4 三种模型抗压强度实际值与预测值散点图

由图4 可以看出，与XGBoost 和LightGBM 相比，CatBoost 回归算法的预测结果主要集中在误差线内。表6 为不同模型误差分析表，CatBoost 模型预测结果在误差线范围内数据个数占总样本数的92.9%，高于XGBoost 和LightGBM 模型，可见CatBoost 模型预测效果最好。

表6 不同模型误差分析表

4 结语

本文建立了基于机器学习回归算法的SAP 混凝土抗压强度预测模型，分析SAP 对混凝土抗压强度的影响，将CatBoost 与LightGBM 以及XGBoost 模型进行对比，得到如下结论：

①当水胶比为0.35 和0.38 时，掺加0.1%和0.3%的SAP 可以提高混凝土的抗压强度，SAP 的“吸水—释水”特性通过控制水化反应程度控制干燥收缩内应力，从而提高混凝土的抗压强度。

②在预测模型的四个输入变量中，水胶比和养护龄期对混凝土强度的贡献率较大，分别为55.5%和36.0%，SAP 掺量和预吸水倍数贡献率较小，分别为4.7%和3.8%。

③相比于LightGBM 和XGBoost 模型，CatBoost 具有更高的精度和更强的泛化能力，其测试集决定系数为0.981，三项评价指标（均方误差、均方根误差和决定系数）均优于LightGBM以及XGBoost模型。

④机器学习回归算法在混凝土抗压强度预测方面有独特的优势，但大部分机器学习模型不能对预测结果进行解释，有关各个特征值之间的交互作用及局部预测有何具体影响的可解释机器学习模型的框架亟需引入。