基于光纤陀螺仪的轨道不平顺精度检测及预测

高鸽子, 孔军

(1.西安铁路职业技术学院,土木工程学院,陕西,西安 710026; 2.西北工业大学,中航工业自控所,陕西,西安 710600)

0 引言

“高速度、高舒适、高安全”是高铁运输一直以来不断追求的目标,这对列车与轮轨也提出了更高要求[1]。平顺的轨道是列车高速行驶的前提,也是行车安全和舒适性的基本保证。如果轨道平顺性不满足要求,则在高速条件下轮轨之间相互作用力增大,伴随的车辆振动、轮轨噪声会使得行车安全性、舒适性极大降低,甚至造成列车脱轨等严重事故。铁路轨道在长期运行中由于列车动载、地基沉降、自然环境侵蚀等诸多原因会出现不同程度的轨道病害,从而影响列车的平顺性[2-3]。高速铁路轨道平顺的高标准要求严格的轨道质量检测和养护,也对铁路工务部门的日常维修养护提出了更大的挑战[4-5]。

相关方面的研究吸引了很多的研究学者。白文飞等[6]根据BP神经网络所具有的强非线性特征,通过递推合成BP神经网络预测轨道的不平顺程度,实现了预测准确性的显著提升。李巍[7]对采集得到的轨道不平顺参数异常情况进行了研究,同时运用灰色预测并结合回归分析方法完成预测过程,根据熵值统计结果获得加权均值,建立了一种通过熵值法实现的轨道运行状态预测模型。同时,林怀青等[8]引入支持向量机与主成分分析方法来辨别轨道的不平顺程度,之后根据各轨道处于特定不平顺状态下的轴箱加速性能测试结果判断此方法的可靠性。为了提高轨道不平顺检测精度,本文通过光纤陀螺仪开展轨道不平顺测试实验,通过支持向量机开展预测分析研究。

1 光纤陀螺仪轨检车原理

1.1 光纤陀螺仪工作原理

假设在一闭合光路中从同一光源形成两束特征相同的光沿相反的方向进行传播,通过两束光在汇聚点产生的光程差推算光纤线圈在空间转动的角速度,即Sagnac效应。

图1为Sagnac效应示意图。X为光束入射点,Y为光束出射点,Ω为角速率。

图1 Sagnac效应示意图

1.2 弦测法原理

基于光纤陀螺仪(FOG)的轨向不平顺检测技术是目前弦测法中一种先进的轨道检测手段[9]。利用陀螺仪测角,通过轨检仪角度改变轨向之间的传递方程,得到轨向不平顺数据。本文结合弦测法获得轨向的机制研究陀螺测角系统的轨向算法。

在陀螺仪使用期间,系统间隔l2/2得到一次陀螺仪工作的角度,如果陀螺仪测角系统第i次获得的角度为A(i+1),则每相邻的两点转动角度即A(i+1)-A(i)[10],如图2所示。

图2 角度推导弦测值原理

C=1/2[A(i+1)-A(i)]

(1)

普通轨道的半径R很大,在步长为l2/2的2个测量点间陀螺转角极小(为了提高精度可以减小步长l2,本文取l2=0.625 m测5 m弦),可近似认为

(2)

代入传递方程,即:

(3)

2 测量结果分析

2.1 试验方案

学校配备校内轨道实训场(见图3),周边环境较好,地质条件稳定,且通视条件良好,为方案实施提供了有利的外界环境。场地轨道线路换算长度约1040 m。其中,无砟轨道约110 m可用于此次轨检仪系统的检测。

光纤陀螺仪为本文用轨检车测量轨道不平顺的主要传感器,它的工作特性关系到轨检设备的精准度。轨道平顺性的检测内容主要包括轨距、超高、高低、水平、轨向等测量。本文主要介绍轨距、水平和轨向。

两钢轨头内侧轨面下16 mm位置之间的距离称为轨距。两钢轨的轨顶高差称为水平。轨距和水平的几何关系示意图如图4所示。

图4 轨距、水平几何关系示意图

轨向表示钢轨顶面下方16 mm轨距水平位置的改变,如图5所示。

图5 轨向不平顺示意图

本文通过对检测场轨道水平、轨距、轨向进行重复测量,验证基于光纤陀螺仪的轨检仪的相关内、外符合测量精度。内符合精度指轨检仪测量系统的稳定性,即轨检仪在对同一段轨道的几何状态参数进行重复测量时,测量结果的差异性。外符合精度表示轨检设备检测的精准性,即其测得结果和轨道几何状态参数基准值的差值要足够小。内符合测量精度是相对差异,外符合测量精度是绝对差异。

本文采用0级数显轨道尺对检测场轨道各标记处的轨距和水平进行正、反3次反复测量,并以其平均值作为轨距、水平的基准值,采用3次人工拉弦轨向平均值作为轨向的基准值。在完成测量后,对实测数据按照标记点号进行编号,然后计算检测场轨道各标记处轨距、水平、轨向正反推测量差值、重复测量差值及各测量值与基准值的差值,并计算其测量精度。

2.2 试验结果

工务车间配发的轨道检测仪,根据其测量数据不同分为两个类别,一是相对轨道信息检测,二是绝对轨道信息检测。2种检测方式分别适用于无轨道控制网下的检测和有轨道控制网下的检测。两种类型设备均采用手推式,绝对检测速率为200 m/h,相对检测速率为4 km/h。通过试验,轨距、水平、轨向内、外符合测量精度计算结果见表1。

表1 内、外符合测量精度结果

从表1可以看出,差值的中误差都满足各自限差要求,说明该轨检仪内符合精度满足要求。轨距测量值与其基准值差值的中误差比中误差限差稍高,但在3%以内,基本满足要求。这种结果可能是因为轨道检测场条件或人为因素引起的0级数显道尺测出的轨距基准值测量精度超限。基于此,认为该轨检仪外符合精度满足要求。

3 轨道不平顺检测精度预测

3.1 支持向量机预测模型

轨道不平顺可以采用轨道质量指数(TQI)作为判断指标。以下为TQI计算式:

(4)

式中,σi表示单项轨道不平顺标准差,xi表示连续采样数据的均值,xij表示单项不平顺程度。

各轨道单元实际收到外部异质因素的干扰,不同轨道单元在TQI数据特征方面也存在一定差异性。本文结合各单元区段的自身特点构建相应的参数变化模型,通常是用支持向量机构建所需的模型。采用支持向量机方法进行回归拟合时需要先设置一个合适的分类面来确保各个训练样本相对分类面达到最低误差。本文通过支持向量机建立的轨道不平顺预测模型步骤见图6。

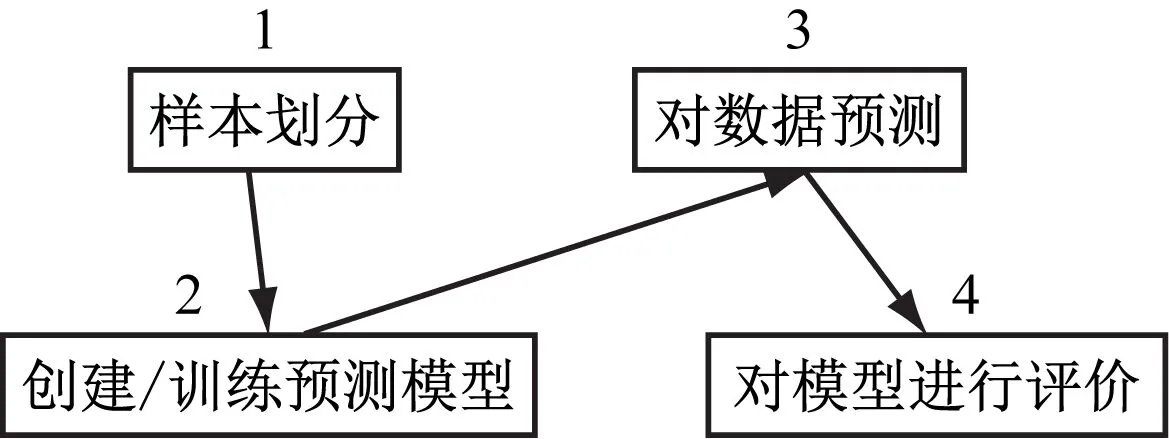
图6 支持向量机轨道不平顺预测模型流程

假定训练集内包含了l个训练样本,在高维特征空间内构建以下回归函数:

f(t)=ωΓ(t)+a

(5)

式中,Γ(t)属于非线性映射函数。ω与a都是变量,采用支持向量机进行处理的具体方式是利用构建优化算法与支持向量机参数进行ω和a的优化求解计算。

ε表示线性不敏感损失函数,该函数具备良好稀疏性能,可以通过设定合适的ε参数来提升结果泛化性能,本次使用以下的损失函数:

(6)

式中,f(t)是由回归函数计算得到的TQI预测数据。

以第1部分TQI参数构建的模型对轨道质量状态变化特征进行预测,可以得到:

f(t)=ω*Γ(t)+a*

(7)

3.2 预测结果分析

根据3.1节提出的预测模型进行预测得到图7的结果。

(a)第1周期

表2是在预测结果基础上进行计算获得的评价指标。本次利用预测模型得到的均方误差与决定系数依次是E=0.013、R2=0.97以及E=0.006、R2=0.96,因此采用此方法获得了较低均方误差,并且获得了接近1的决定系数,表明采用此方法构建的预测模型满足可靠性要求。

表2 轨道不平顺预测性能评价结果

4 总结

采用人工拉弦对检测场轨道的左右轨轨向进行测量,通过实验数据分析,验证了某基于光纤陀螺仪轨检车测量轨向的内、外符合测量精度。本方案可以实现5 km/h的绝对测量和10 km/h的相对测量,能较好地满足目前高铁运输的需求。建立了支持向量机预测模型,获得了较低均方误差,并且获得了接近1的决定系数,表明此方法构建的预测模型满足可靠性要求。