柔性定位平台的瞬态动力学分析及疲劳寿命分析
姜薄士,张璐凡,张鹏启,闫恒
(河南工业大学机电工程学院,河南郑州 450001)
0 前言
随着现代工业的飞速发展,微纳产品的关注度在逐渐提高,超高加速度宏微运动平台是一个超精密定位平台,可实现微米甚至纳米级别的定位[1-2],为微纳产品的发展提供的条件。柔性定位平台是超高加速度宏微运动平台的关键部件,平台的定位工作均是在柔性定位平台上来完成的,所以,平台结构的稳定性、可持续工作性有着重要作用。疲劳分析经过多年的发展,已经在许多机械结构上得以应用[3-5]。其中卢宁、韩崇瑞[6]联合了ADAMS、ANSYS和nCode Design Life计算出了塔式起重机起重臂疲劳寿命。蔡新等人[7]探究了在不同工况载荷下风力机叶片的疲劳损伤情况,获得了叶片在风速大、强度高的工况下最易发生疲劳损伤。刘迪辉等[8]对取力器螺栓展开研究,发现空压机转速越低,螺栓寿命越短,并获得了空压机的转速,避免螺栓在使用早期就发生断裂。
柔性定位平台是受音圈电机和压电致动器的驱动力来完成工作,定位工作是在驱动力的往复循环下进行的,所以,对其进行疲劳分析,探究柔性定位平台在驱动力作用下的疲劳情况具有很大意义。文中主要研究内容为,首先建立柔性定位平台的三维模型,利用刚度公式计算出柔性定位平台的载荷大小,并对柔性定位平台分别进行静力分析和瞬态动力学分析,探究其力学性能,获得了平台的危险点部位及疲劳分析所用应力谱,最后结合Goodman曲线评估方法对柔性定位平台进行了校核计算,利用nCode进行疲劳分析,获得柔性定位平台的疲劳寿命。
1 柔性定位平台介绍
文中所用的超高加速度宏微运动平台是由连接臂、柔性定位平台、音圈电机、压电促动器、导轨架、基座和大理石隔振平台等构成。其中柔性定位平台是超高加速度宏微运动平台的关键装置,平台的定位工作是在柔性定位平台上进行的,主要由音圈电机和压电促动器提供驱动力来完成定位工作,对柔性定位平台进行研究,将有很大意义。
1.1 工况分析
超高加速度宏微运动平台在定位过程中会受多种工况的作用,文中研究的工况为柔性定位平台微定位下的工况,即音圈电机不产生驱动,柔性定位平台受到压电驱动器正向作用力作用。边界条件等效为平台左右两端面全约束,压电驱动器驱动力作用在平台内,如图2所示。
1.2 模型导入和网格划分
文中所用模型是在SolidWorks中建立的,模型去除了一些螺栓孔和定位孔,它们都分布在不太重要的部位,所以不影响最终分析结果,还可以提高工作效率,增加网格精度。之后,将处理后的模型导入到ANSYS Workbench中进行网格划分、材料赋予、边界条件施加和分析结果导出。网格质量的好坏会影响结果的精度,网格划分是有限元前处理中至关重要的一步。文中用四面体和六面体结合的方式进行网格划分,在受载荷作用较小的部位用四面体网格进行划分,在受荷载作用较大的部位用效果更好的六面体网格划分,这样可以节省网格划分时间,又能保证精度。柔性定位平台所用材料为7075Al-T6,具体数据如表1所示。
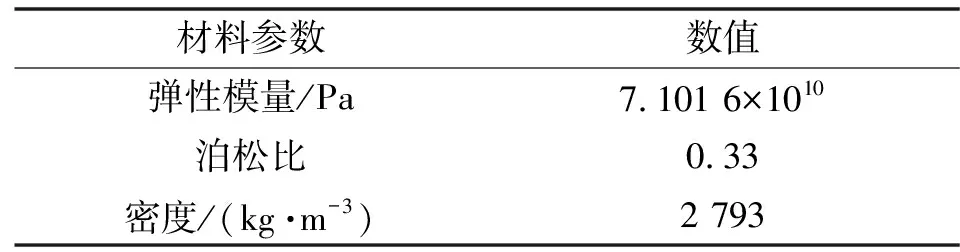
表1 7075Al-T6材料属性
1.3 受力分析
在工作中,柔性定位平台主要受压电促动器的驱动力作用,文中所用的压电促动器为芯明天公司设计制造的,型号为PSt150/14/40 VS20,具体参数如表2所示。

表2 压电促动器PSt150/14/40 VS20参数
在压电促动器促动柔性定位平台移动的时候,压电促动器的移动位移量与柔性定位平台的移动位移量并不相同,可以用以下公式[9]算出柔性定位平台的实际位移量。
压电驱动器输出的最大位移为
(1)
式中:Lmax为压电陶瓷最大名义伸长量;Kpzt为压电促动器刚度;Ka为柔性定位平台刚度;L为柔性定位平台最大输出位移。
由柔性定位平台输出的位移也能算出压电陶瓷输出的最大驱动力F:
K=F/L
(2)
F=KL
(3)
柔性定位平台的刚度可以用有限元来算出,也可以用理论公式算出,文中用两种方法分别计算了柔性定位平台的刚度。
1.3.1 理论公式
柔性定位平台是由8个柔性铰链组成的双平行四杆机构,算出单个柔性铰链的刚度,就能算出柔性定位平台的刚度。图3和表3所示为直圆型柔性铰链的参数。

表3 直圆型柔性铰链参数
柔性铰链的转动刚度[10]为
(4)
式中:Mz为对柔性铰链施加的力矩;αz为在弯矩作用下柔性铰链的转角;E为材料的弹性模量。
(5)
式中:s=R/t。
由材料力学能量法的原理可知,外力所做的功等于每构件产生的弹性应变能总和,导向机构在力f作用下产生位移s所做的功转变为铰链变形的弹性势能[11-12]。
(6)
双平行四杆机构的刚度为
(7)
式中:l为柔性铰链之间距离。
代入相关数据,得柔性铰链刚度为
Ka=34.17 N/μm
1.3.2 有限元计算
有限元计算刚度是利用静力分析,算出柔性定位平台在单位力下移动的位移,利用刚度计算公式算出柔性定位平台的刚度。前面已经完成了柔性定位平台模型的搭建与所用材料特性设置,有限元模型所用材料为7075Al-T6,此材料存在于ANSYS Workbench材料库中,所以不用额外添加,直接调用即可。柔性定位平台两边固定约束,载荷设置为1 N。完成上述步骤后,即可输出柔性定位平台的位移云图,如图4所示。
如图4所示,在单位载荷的作用下,柔性定位平台的位移为3.31×10-8m,由刚度计算公式可得柔性定位平台得刚度如下:
(8)
由表4可知:有限元刚度与理论刚度相差11.59%。文中用有限元刚度来进行柔性定位平台的位移与驱动力计算。

表4 有限元刚度与理论刚度对比
根据公式可以算出柔性定位平台的实际输出位移与驱动力。
30.36 μm
(9)
Fmax=KaL=30.21×30.36=917.18 N
(10)
由上述公式得出在压电致动器输出最大位移时,柔性定位平台实际输出位移为30.36 μm,获得的最大驱动力为917.18 N。
1.4 静力分析
将算出的最大驱动力作为载荷对柔性定位平台进行静力分析,获得柔性定位平台的应力云图和位移云图。
由图5和图6可知:柔性定位平台的最大应力为6.63×107Pa,远低于柔性定位平台所用材料的屈服强度。柔性定位平台最大位移为30.38 μm,与计算出的柔性定位平台的基本一致,也确保了计算的准确性。
2 瞬态动力学分析
瞬态动力学分析是确定载荷随时间变化的结构动力响应的过程,输入随时间变化的载荷数据,如稳态载荷和瞬态载荷等,输出随时间变化的应力应变等数据[13]。
压电驱动器输出的载荷曲线为正弦信号载荷,峰值为柔性定位平台实际输出的最大位移,最大位移在前面已经计算得出,频率为柔性定位平台在实际定位过程中所采用的驱动频率,文中以频率的大小来预测柔性定位平台的疲劳寿命。位移载荷曲线与驱动力载荷曲线是成线性关系的,所以,位移时间曲线与载荷时间曲线形状是一致的。文中使用频率为 1 Hz 的载荷曲线对柔性定位平台做瞬态动力学分析,得出柔性定位平台的应力与位移曲线,图7所示为柔性定位平台所受力载荷曲线。
将柔性定位平台三维模型导入到ANSYS Workbench中,进行网格划分、材料设置和载荷步数的设置,之后,进行瞬态动力学分析,获得柔性定位平台在各个步数上的应力云图和位移云图,以及应力-时间曲线和位移-时间曲线,可以用作疲劳分析。
从图8可以看出:柔性定位平台应力最大的位置在柔性铰链处,为3.84×107Pa,出现了应力集中现象,其他部位应力集中现象不明显。如图9所示:柔性定位平台中间部位为整体向Z轴方向移动,位移为1.76×10-5m。
图10所示为应力与各个子步之间的关系曲线,也就是柔性定位平台危险部位的应力-时间历程,最大应力为6.63×107Pa,最小应力为291.80 Pa。图11所示为位移与各个子步之间的关系曲线,最大位移为3.04×10-5m,最小位移为1.27×10-7m。
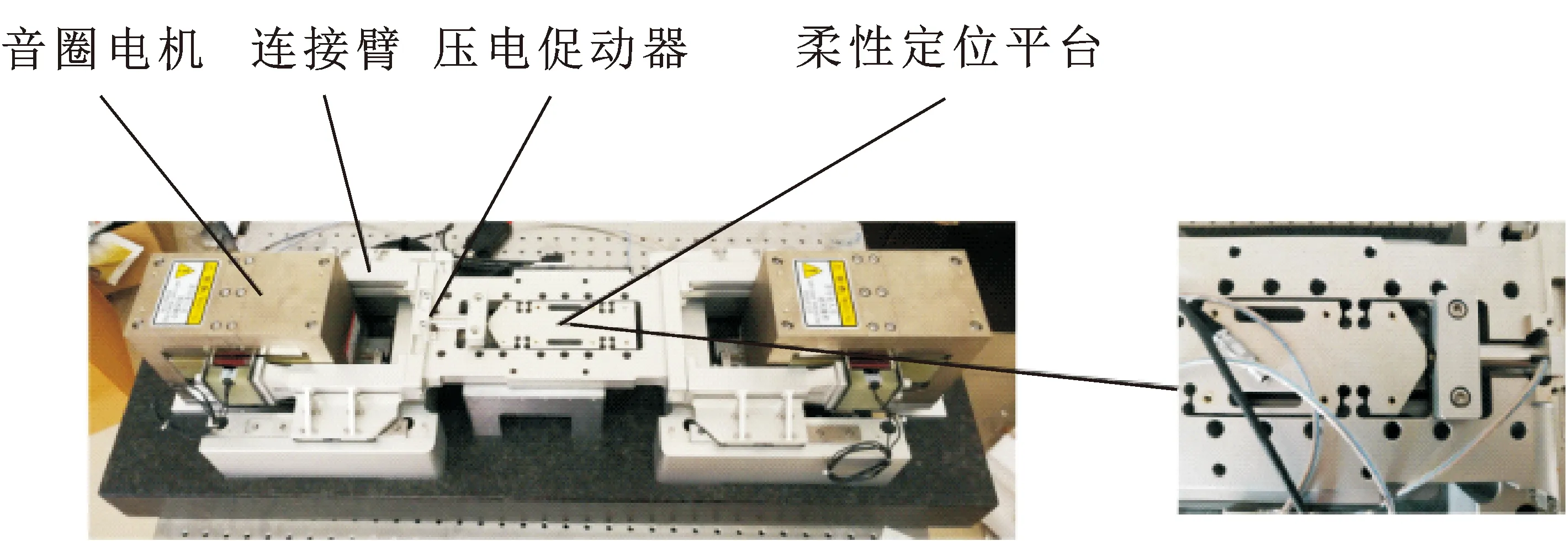
图1 超高加速度宏微运动平台
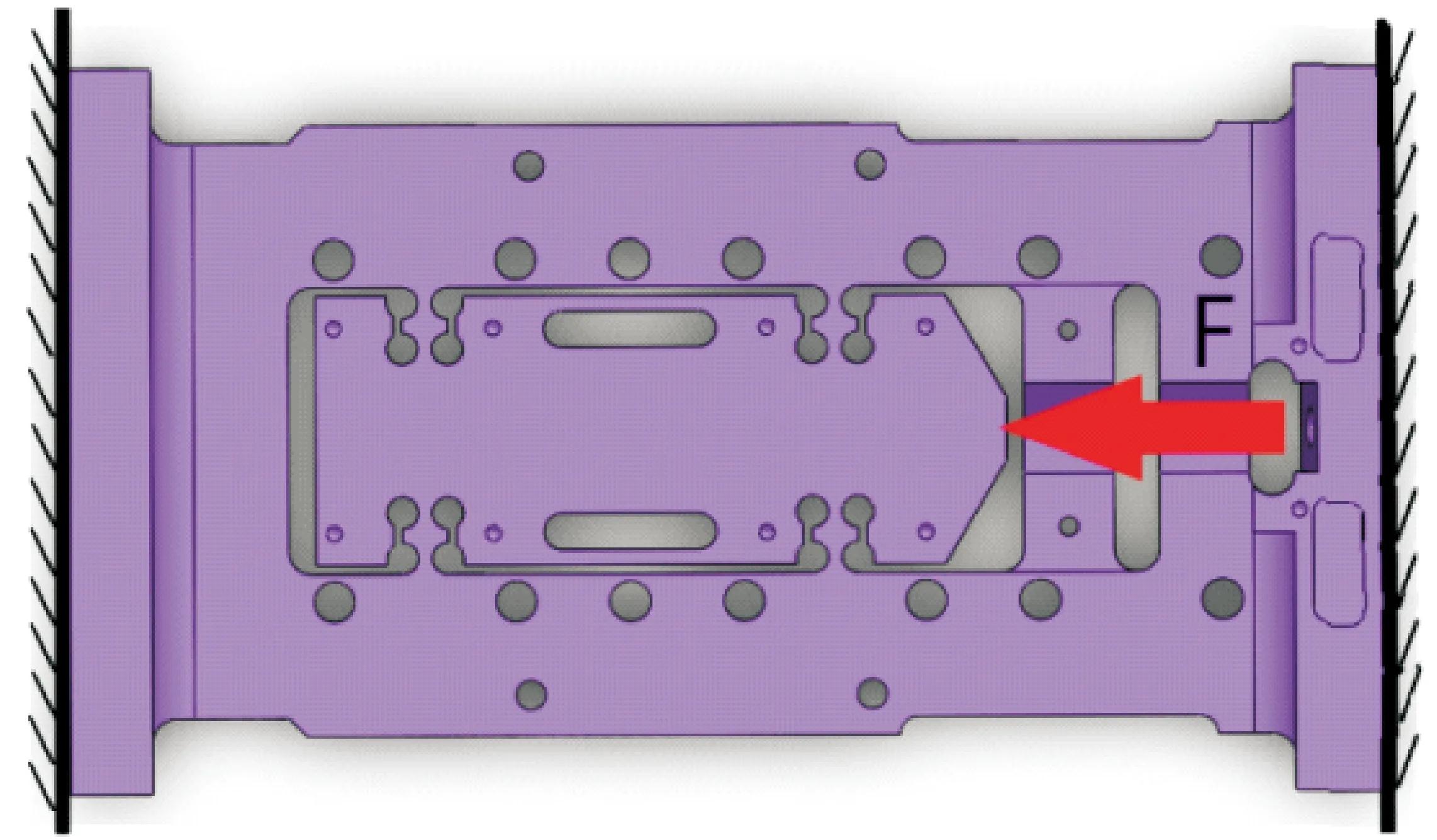
图2 柔性定位平台受力简图
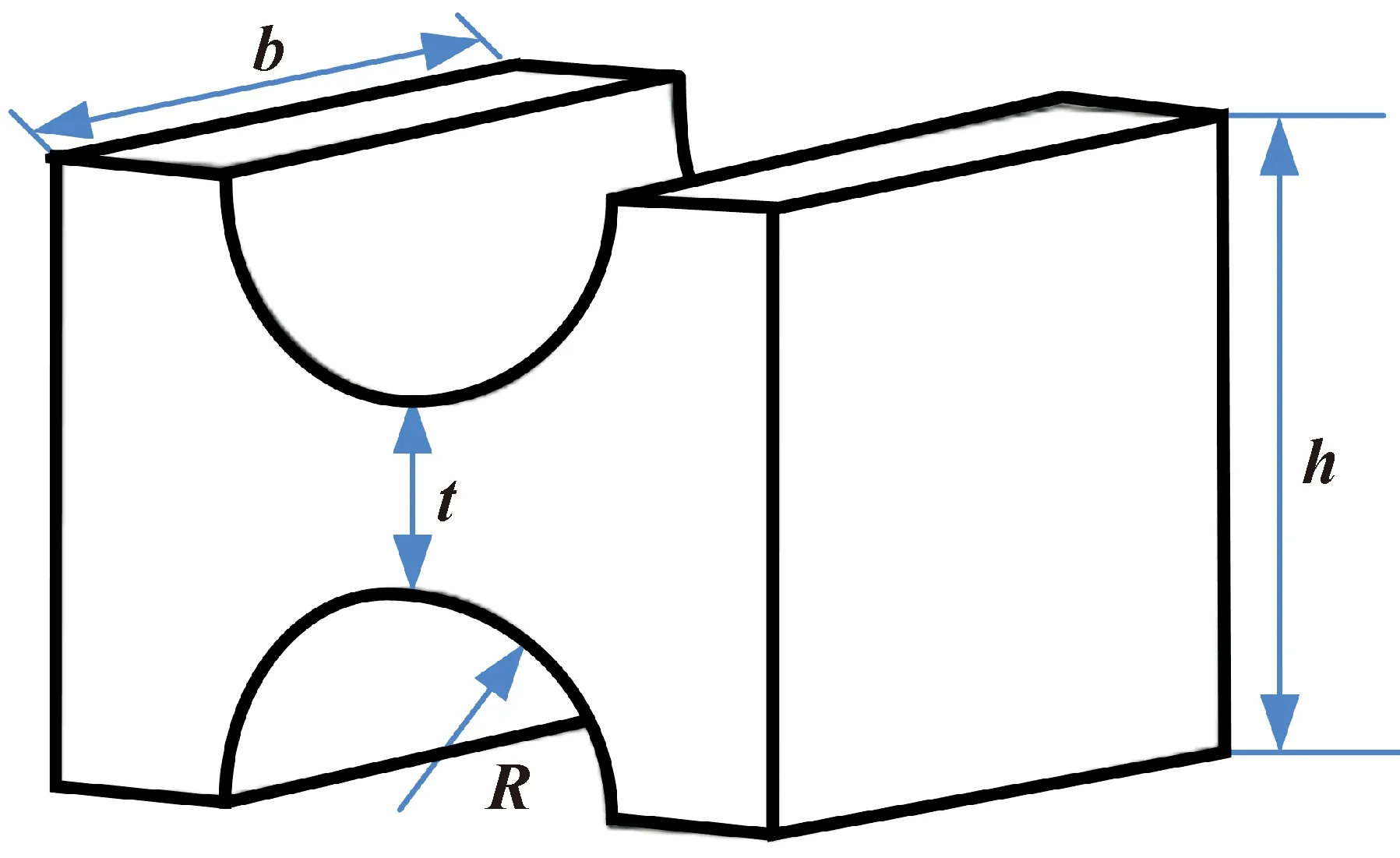
图3 直圆型柔性铰链
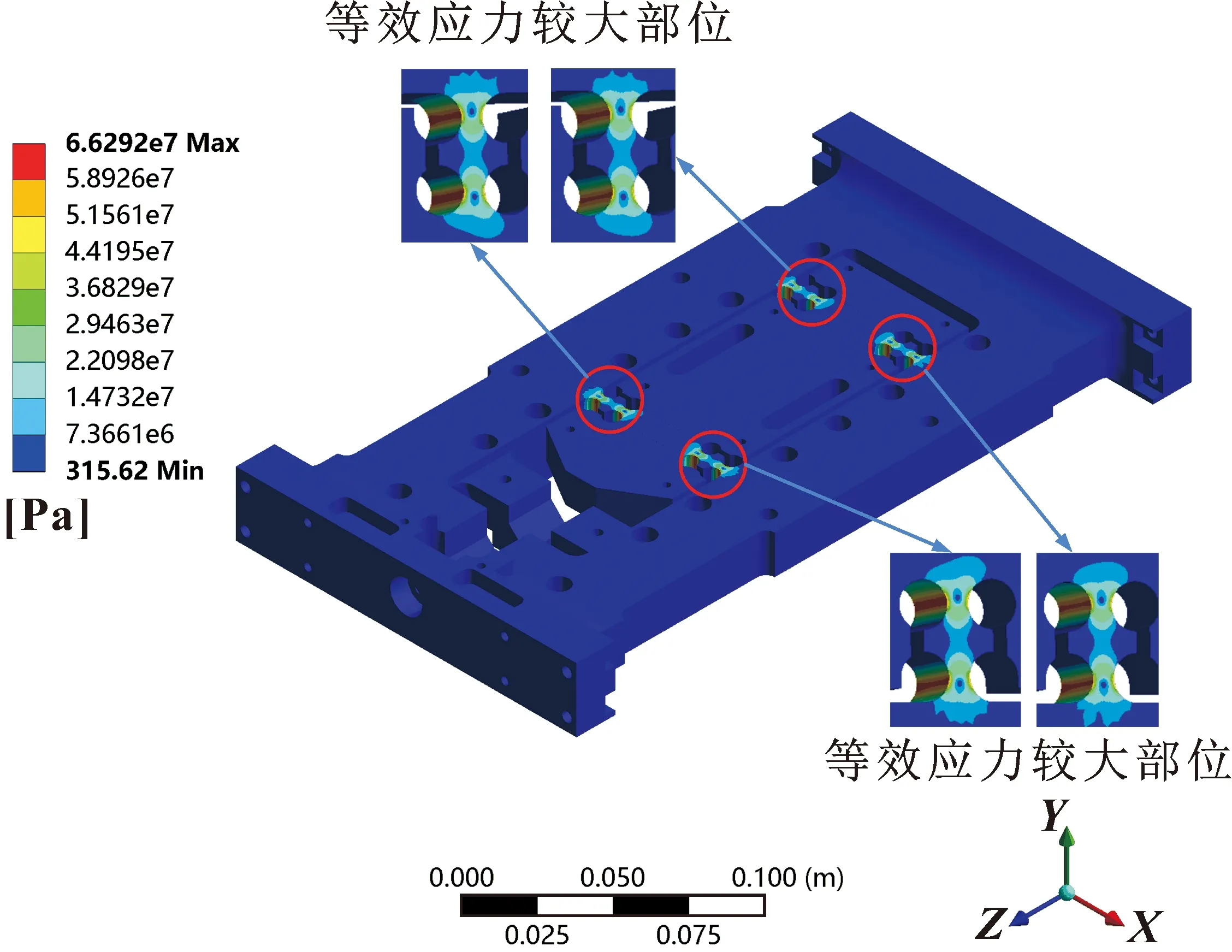
图5 柔性定位平台应力云图

图6 柔性定位平台位移云图
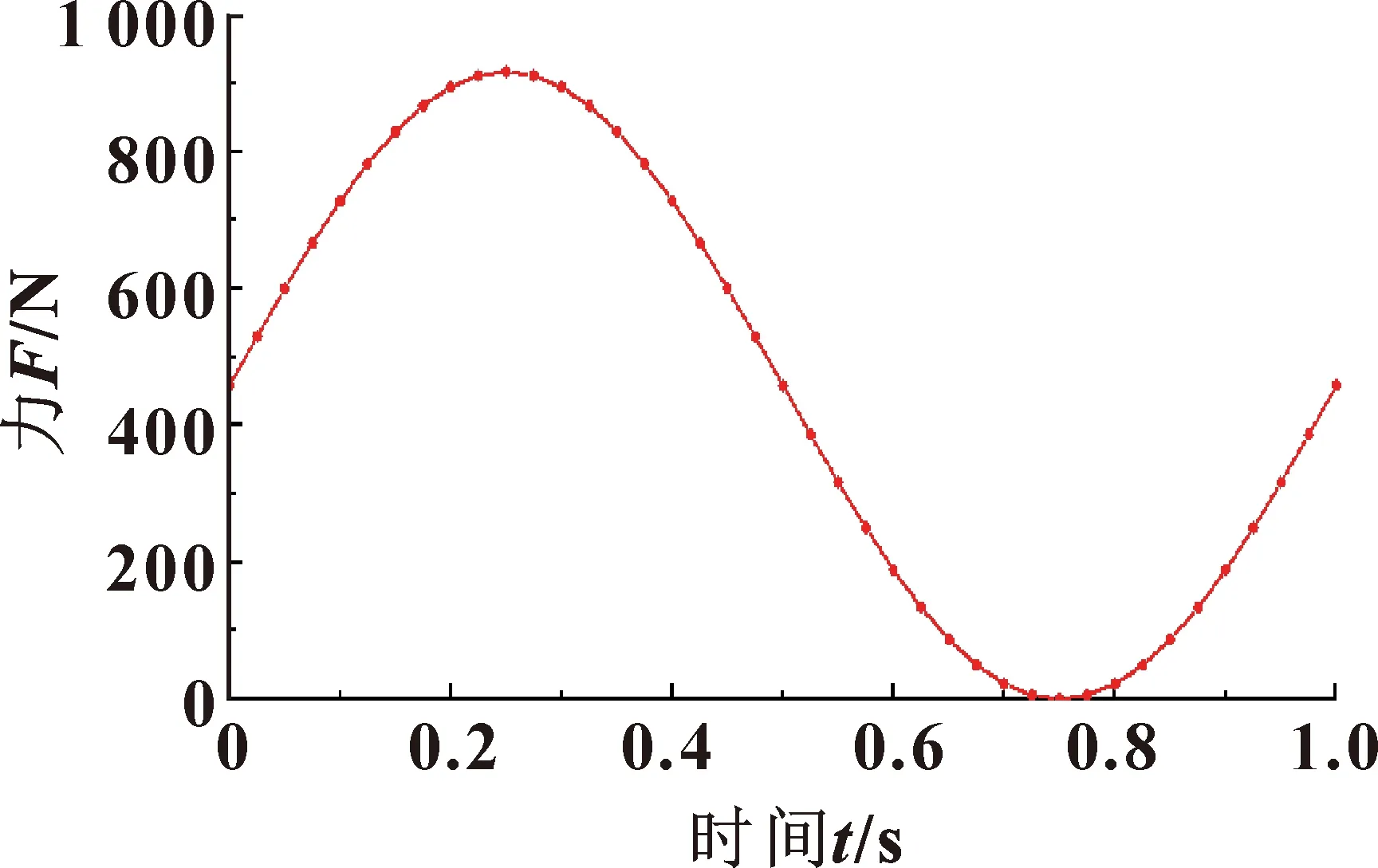
图7 力载荷曲线

图8 柔性定位平台在第1个载荷步的等效应力云图

图9 柔性定位平台在第1个载荷步的位移云图
3 疲劳分析
3.1 Goodman疲劳极限线图
目前,国际上许多国家用Goodman疲劳极限线图对机械结构进行疲劳强度校核,它可以保证结构在任何载荷下能够安全工作。本文作者用Goodman-Smith疲劳极限图进行疲劳强度校核,它是以横坐标为平均应力、纵坐标为最大最小应力的形式表现出来,内容丰富,形式简单,容易表达,使用最为广泛。
Goodman-Smith疲劳极限图的绘制需要知道材料强度极限、疲劳极限和屈服极限,文中使用的材料强度极限约为570 MPa,屈服极限约为500 MPa,疲劳极限约为170 MPa。疲劳极限由材料的S-N曲线获得,也可以通过经验公式获得。文中根据文献[14]中的材料疲劳极限经验公式得出的疲劳极限为168 MPa,根据软件中提供的材料S-N曲线获得的疲劳极限约为170 MPa,两者相差不大,故能证明疲劳极限的准确性。使用文献[15]中的绘图方法,绘制出Goodman-Smith疲劳极限图,如图12所示。
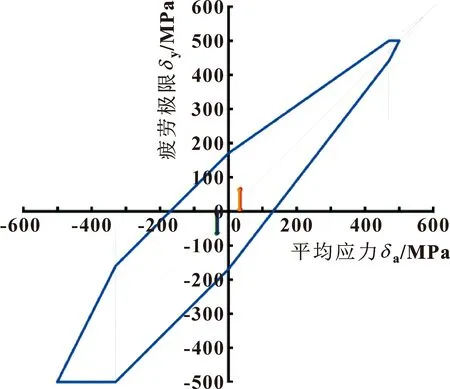
图12 Goodman-Smith疲劳极限评估图
图13和图14分别为柔性定位平台最大主应力云图和最小主应力云图,可知:柔性定位平台柔性铰链部位受到载荷作用较大。所以,文中评估点的选择为柔性铰链的16个圆弧部位。
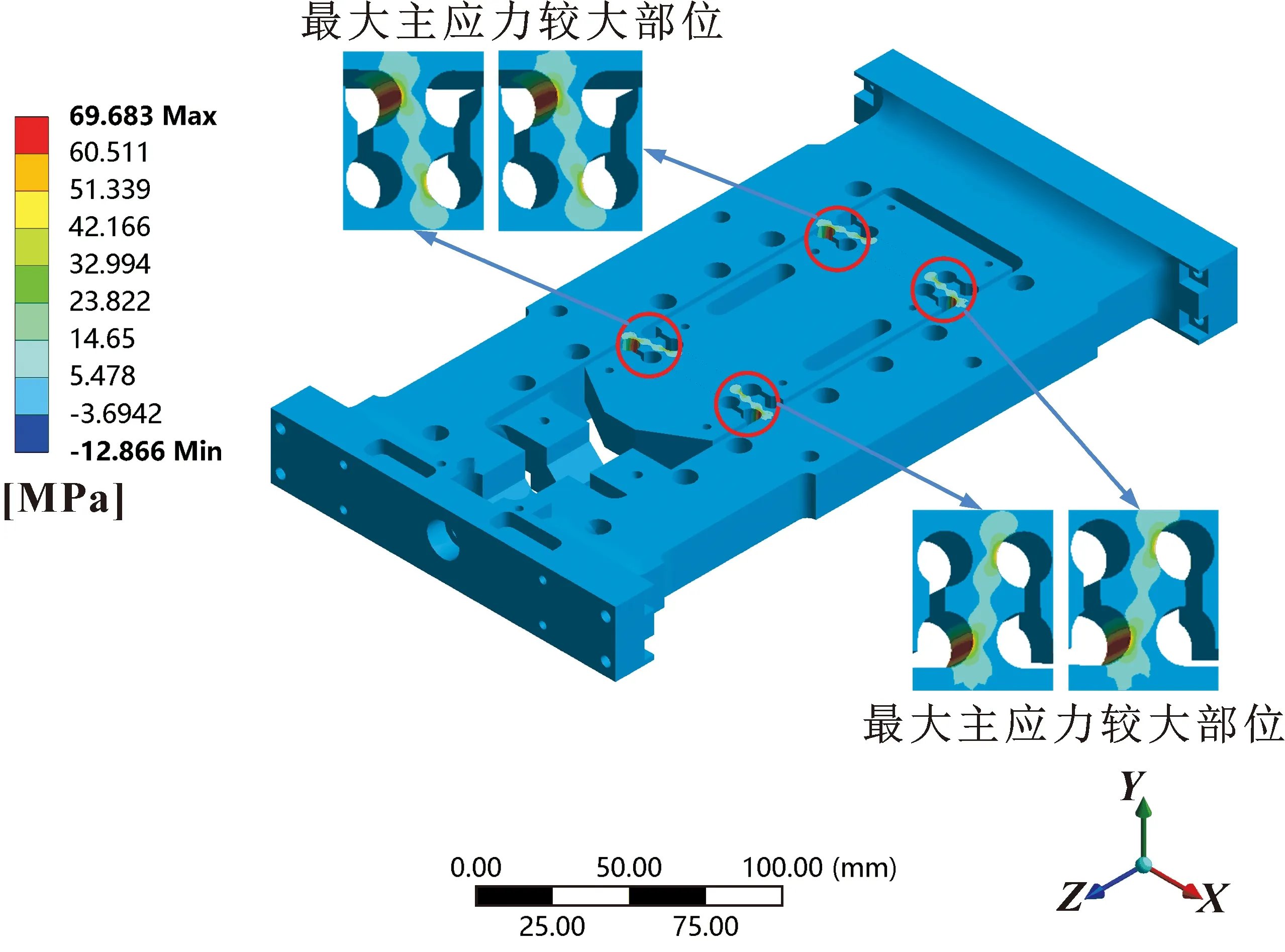
图13 柔性定位平台最大主应力云图

图14 柔性定位平台最小主应力云图
已知柔性定位平台危险部位为柔性铰链处,选取柔性铰链上圆弧部位的16个节点,根据公式算出评估点的平均应力和应力幅,如表5所示。
将表5中的数据,在Goodman-Smith疲劳极限线图中进行评估,评估结果如图12所示。
如图12所示,每个节点均位于Goodman-Smith疲劳极限线图的封闭线内,且与封闭线有一定的距离,即表示柔性定位平台的疲劳强度可靠性较高,发生疲劳破坏的可能性较低。
3.2 nCode Design Life疲劳分析
疲劳分析可以分为疲劳分析方法的选择、有限元分析结果的求解、S-N曲线和载荷谱的输入以及疲劳分析结果的输出。疲劳分析有很多方法可以使用,其中名义应力法、局部应变法和应力场强法使用较为广泛,文中使用名义应力法进行疲劳分析。
图15所示是在nCode中进行疲劳分析的分析流程,首先建立有限元模型,对有限元模型进行瞬态动力学分析获得应力谱,然后导入到nCode Design Life中对柔性平台进行分析,其中包括一些参数的设置,最终获得柔性定位平台的疲劳损伤和疲劳寿命。

图15 名义应力法疲劳分析流程
选用前面所用瞬态动力学分析结果导入到nCode Design Life中。载荷谱为瞬态动力学分析得出的应力谱,在分析中,载荷谱直接导入到了nCode Design Life中,不需要再额外添加,材料的S-N曲线是在nCode Design Life材料库中提取的,并用Goodman法对S-N曲线进行修正。
完成上述设置后,得到柔性定位平台的损伤和寿命云图。
如图16和图17所示,柔性定位平台寿命最低点位于柔性铰链上,说明柔性铰链是柔性定位平台的薄弱部位,在压电致动器驱动频率为1 Hz时,柔性定位平台疲劳寿命为3.52×1013次。

图16 柔性定位平台的损伤云图

图17 柔性定位平台的寿命云图
表6所示为当柔性定位平台的驱动频率变化时,柔性定位平台的疲劳寿命。

表6 柔性定位平台的疲劳寿命
由表6可知,柔性定位平台的疲劳寿命随着压电促动器的驱动频率升高而降低。超高加速度宏微运动平台是超高速精确定位装置,保证宏微运动平台在超高速运行下,有着较长的使用寿命是一个必要的研究工作。文中得出了柔性定位平台使用寿命随着驱动频率的增加而降低,获得了具体疲劳寿命数值,对宏微运动平台的设计提供了参考。
4 结论
文中联合SoilWorks、ANSYS Workbench和nCode Design Life对超高加速度宏微运动平台进行了静力分析、瞬态动力学分析和疲劳分析,获得以下结论:
(1)利用三维软件和有限元技术建立柔性定位平台的三维模型和有限元模型,利用刚度公式计算出了柔性定位平台所需驱动力,在有限元软件中对柔性定位平台进行静态力学分析,获得了柔性定位平台危险点的位置及应力变形数据;
(2)对柔性定位平台进行瞬态动力学分析,得到柔性定位平台应力和变形随时间变化曲线,并输出柔性定位平台疲劳分析所用的应力-时间历程,用于疲劳分析;
(3)在柔性定位平台疲劳分析中,绘制出了柔性定位平台Goodman疲劳极限线图,评估了柔性定位平台在静态力作用下的疲劳强度,并获得了柔性定位平台的疲劳寿命和疲劳损伤,其中在驱动频率为1 Hz时,柔性定位平台的疲劳寿命为3.52×1013次,随着频率的增加柔性定位平台的疲劳寿命在降低。

