螺杆式连续油管水力振荡器轴向力及其影响因素分析
黄瑞,刘少胡,2,吴远灯,张磊
(1.长江大学机械工程学院,湖北荆州 434023;2.长江大学油气钻采工程湖北省重点实验室,湖北武汉 430100)
0 前言
随着浅层井的持续开发,浅层油气藏逐渐减少,油气井开采逐渐向深层甚至超深层迈进,超深长水平段大位移油气井已经成为提高油气藏勘探开发效益的新技术。较普通定向井和直井,其穿透油藏的井段更长,因此可有效增加泄油面积、提高单井产量、降低开发成本。新疆、涪陵等地油气井井深普遍较深,斜深达4 500 m以上,水平段长1 500 m以上。2022年10月27日中国石化江汉油田涪陵页岩气田焦页18-S12HF井顺利完井,完钻井深7 161 m,水平段长4 286 m,水平段“一趟钻”进尺4 225 m,一举刷新我国页岩气井水平段最长、水平段“一趟钻”进尺最长两项纪录。同时,长水平段大位移油气井井身结构较为复杂,钻进过程中,随着井眼的加深,摩阻不断扩大,定向拖压严重,钻压传递困难,制约了井眼轨迹的控制及钻进效率的提升。为有效解决上述问题,国内外研发了许多类型的井下降摩减阻工具,包括旋转导向工具、钻柱扭摆钻井系统、水力振荡器等。其中,水力振荡器降摩减阻效果好,能有效降低滑动钻进摩阻,缓解滑动拖压,提高定向效率,被广泛应用在大斜度井、大位移井、长水平段井等的钻井过程中。
此外,在连续油管钻磨桥塞作业中,连续油管管径小、柔性大,且下入过程中摩擦力大,在井下极易发生螺旋屈曲[1]锁死而无法继续下入。水力振荡器能够有效降摩减阻,延迟螺旋屈曲锁死,增加连续油管的下入深度。目前,一些学者对钻井用水力振荡器进行了研究,得出一些结论为连续油管应用提供支撑[2-7]。2020年,于志军等[8]建立了连续油管在水平井各段下入过程中与流体相互作用的载荷计算模型,得出了使用水力振荡器可增加连续油管水平井作业下入深度的结论。2021年,AL-SAIOOD等[9]新设计和开发的连续油管水力振荡器可有效增加连续油管的延伸范围,减少了静摩擦,并将静摩擦转化为连续油管管柱的动摩擦从而减少了螺旋屈曲的发生,降低了阻力。2022年,刘妍言等[10]通过对超长水平井连续油管下入影响因素分析和筛选,利用经典管柱力学进行影响因素定量计算分析,提出加入水力振荡器来降低摩擦因数,能够有效提高连续油管的下放深度。2022年,乔凌云等[11]探究了连续油管水力振荡器断裂失效原因,失效的主要原因是连续油管水力振荡器定子在交变应力和含砂流体冲蚀的共同作用下产生疲劳和冲蚀缺陷,最终导致断裂失效。上述一些学者对连续油管水力振荡器下入深度、降摩减阻性能以及失效形式进行了研究,指明了连续油管水力振荡器能够有效增加连续油管下入深度,但未研究水力振荡器在连续油管中的力学模型和关联性影响因素。
针对以上问题,本文作者将根据连续油管水力振荡器工作过程中的运动和受力分析,得出其轴向力计算模型。采用灰色关联度法,分析动阀板偏心孔半径、动阀板偏心孔偏心距、静阀板孔半径、转子偏心距、动阀板壁厚、流量以及流体密度7个影响因素对连续油管水力振荡器轴向力的影响程度,并进行实例计算,获得影响因素对轴向力的影响规律。
1 螺杆式水力振荡器轴向力分析
1.1 应用工况及功能分析
目前,国内外学者以及研究机构已经成功研制出多种类型水力振荡器,具体可分为螺杆式、阀式、射流式、自激式以及涡轮式等[12],其中最常用的是螺杆式水力振荡器。
与钻井用螺杆式水力振荡器相比,连续油管钻磨桥塞用水力振荡器尺寸更小,为小直径井下工具,一般尺寸7.3 cm(2.875 in),如图1所示,主要由轴向振动短节、动力系统和阀门系统三部分组成[13]。流体通过水力振荡器,带动单头螺杆转动,单头螺杆通过转接头与动阀板连接,使动阀的运动表现为自转和绕工具中心周转的复合运动形式。动阀板偏心孔与定阀板孔重合部分即为过流面积,过流面积随动阀板的运动周期性改变。过流面积的周期性改变使阀组两端产生周期性的压降,获得相应的轴向力,达到振荡作用。

图1 螺杆式连续油管水力振荡器工作示意
连续油管水力振荡器可打破连续油管和套管间的摩擦平衡,将静摩擦转变为动摩擦,减少连续油管的螺旋屈曲现象,提升连续油管下入效率,增加连续油管下入深度。
1.2 运动分析
螺杆式连续油管水力振荡器,采用单头螺杆且动阀板孔偏心,如图2所示,动阀的运动表现为自转和绕工具中心周转的复合运动形式[14-16]。

图2 截面示意
动阀板偏心孔圆心轨迹参数方程为
(1)
式中:E为马达转子偏心距,mm;e为动阀板偏心孔偏心距,mm;ω为自转角速度,rad/s。
(2)
式中:Q为马达总流量,μL/s;η为容积效率;R为转子半径,mm;h为单头螺杆螺距,mm。
静阀板孔圆心O2始终与螺杆轴心O重合,则动阀板偏心孔与静阀板孔圆心距为
(3)
动阀板偏心孔与静阀板孔相交弦可分两种情况,如图3所示。

图3 过流面积变化情况
情况一:动阀板偏心孔圆心O1和静阀板孔圆心O2在相交弦同侧。
r1≥r2时
(4)
此时弦长
(5)
式中:r1为动阀板偏心孔半径,mm;r2为静阀板孔半径,mm。
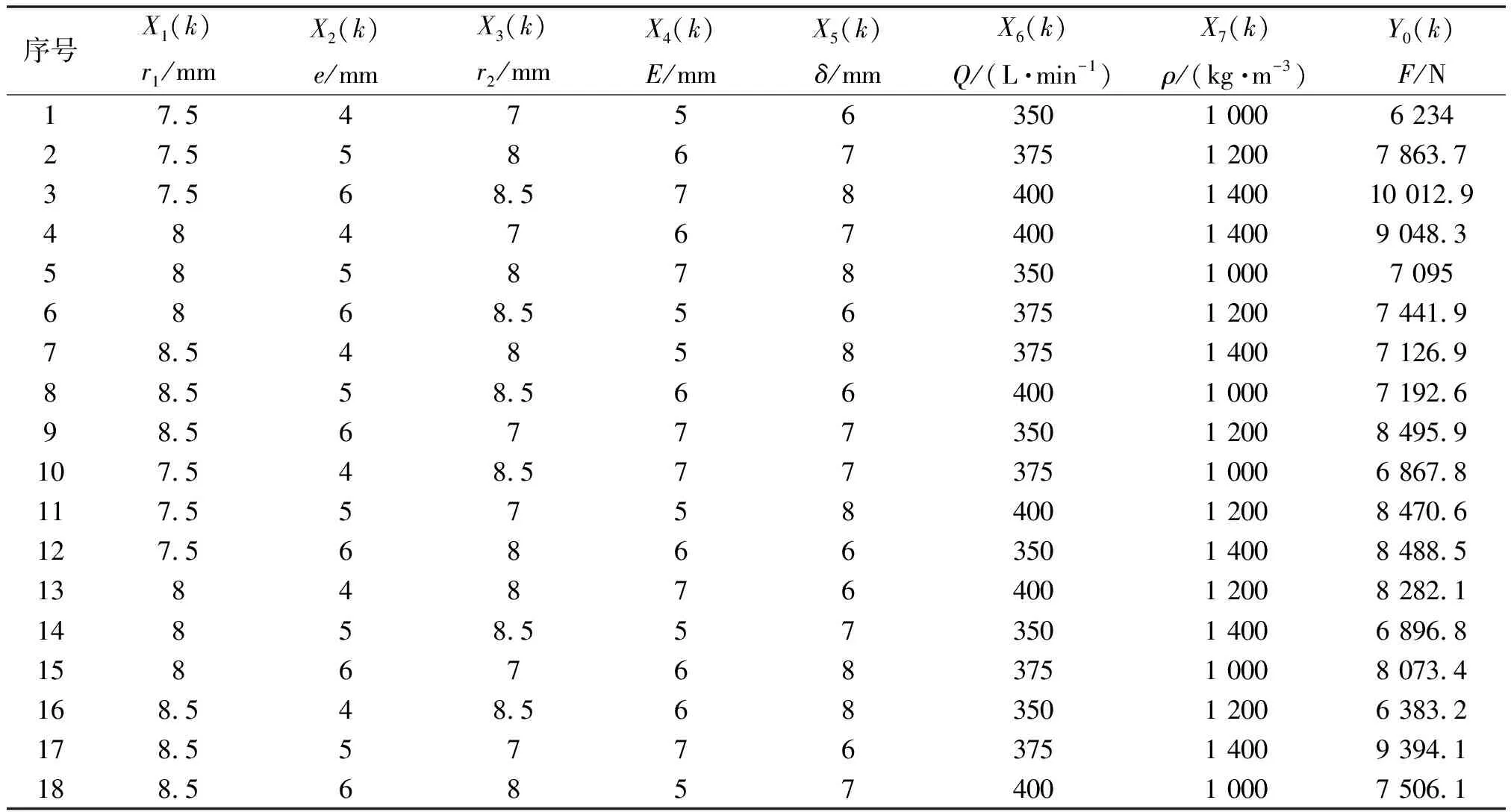
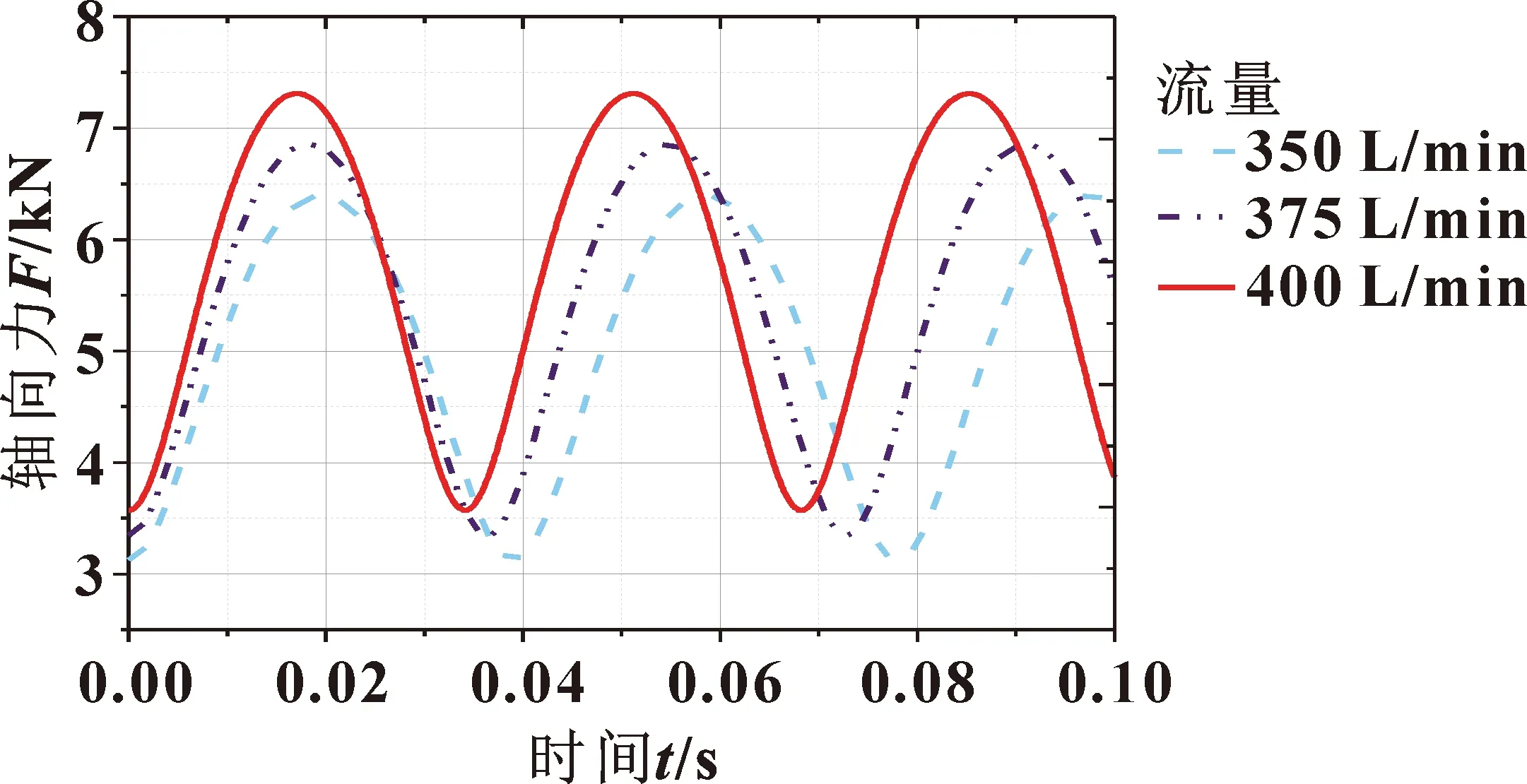
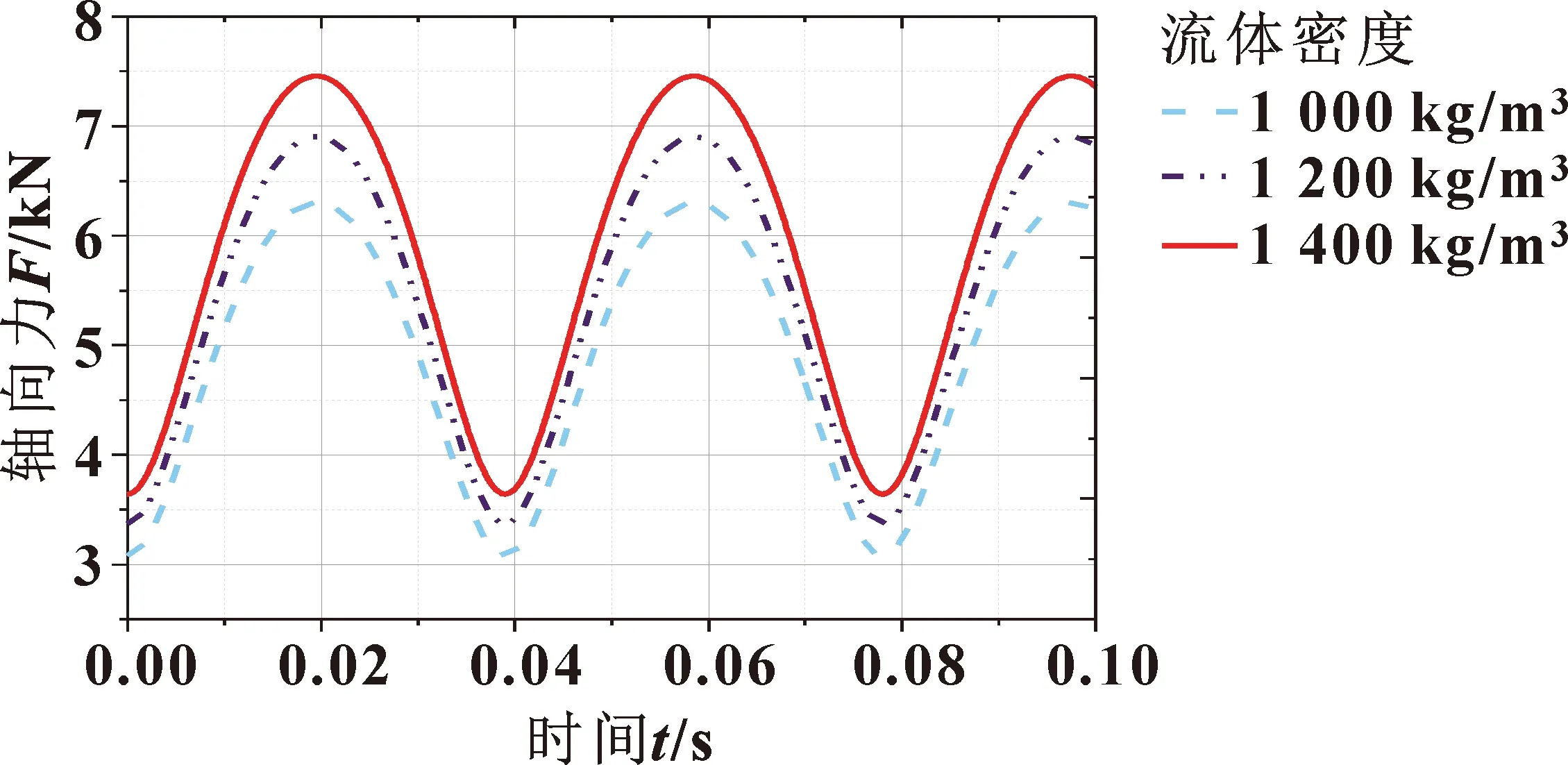
r1 情况二:动阀板偏心孔圆心O1和静阀板孔圆心O2在相交弦异侧。 (6) 此时弦长 (7) 相交弦对应在圆O1和O2上圆心角为θ1、θ2,则 (8) 动阀板在运动过程中偏心孔和静阀板孔重合面积,即过流面计算可以分为同样的两种情况。 情况一:动阀板偏心孔圆心O1和静阀板孔圆心O2在相交弦同侧。 r1≥r2时 (9) r1 (10) 情况二:动阀板偏心孔圆心O1和静阀板孔圆心O2在相交弦异侧。 (11) 螺杆式连续油管水力振荡器受力包括转子轴向力、作用在阀片部分的静压力和由于过流面积变化作用于静阀板上的水击力[17]。转子轴向力和作用在阀片部分的静压力受力方向相反,相互抵消之后相比于水击力可以忽略。因此,文中螺杆式连续油管水力振荡器轴向力只考虑由于过流面积变化作用于静阀板上的水击力: pa=ρcv1 (12) 式中:ρ为流体密度,kg/m3;c为压力传播速度,m/s;v1为动阀板偏心孔处速度,m/s。 动阀板偏心孔处速度为 v1=Q/A1 (13) 式中:A1为动阀板偏心孔面积,mm2。 压力传播速度[18]为 (14) 式中:K为流体弹性模量,MPa;δ为动阀板壁厚,mm;E1为管壁材料弹性模量,MPa。 则水力振荡器所受轴向力为 F=pa(A1-S) (15) 螺杆式连续油管水力振荡器的轴向力大小主要与两方面因素有关:(1)外界泵流量、流体密度;(2)水力振荡器自身结构参数,包括动阀板偏心孔半径、动阀板偏心孔偏心距、静阀板孔半径、转子偏心距、动阀板壁厚。 灰色关联度分析[19]是灰色系统理论中十分活跃的一个分支,可以用来判断不同序列之间的联系是否紧密。文中利用该方法来判断各影响因素与水力振荡器轴向力之间的紧密程度,找出对水力振荡器轴向力影响最大的几个因素。根据江汉石油工程有限公司7.3 cm(2.875 in)螺杆式水力振荡器尺寸参数,各影响因素取值如表1所示。 表1 影响因素取值范围 利用正交试验法获得动阀板偏心孔半径、动阀板偏心孔偏心距、静阀板孔半径、转子偏心距、动阀板壁厚、流量以及流体密度7个影响因素下最大轴向力,如表2所示。其中,反映系统行为特征的数据序列,称为参考数列Y0(k),即最大轴向力;影响系统行为的因素组成的数据序列,称为比较数列Xi(k),即各个影响因素。 表2 不同影响因素下最大轴向力 由于各参数的量纲不一致,不便于进行比较或进行比较时难以得到正确的结论。为更加全面地反映原始数据中各影响因素的变异程度和相互影响程度的信息,在进行灰色关联分析之前,需对数据进行量纲一化处理,文中采用均值法: k=1,2,…,m (16) (17) 不同序列下,各影响因素与轴向力关联系数ξi(k)为 ξi(k)= (18) 将各个序列的关联系数求平均值,作为各个影响因素与轴向力间关联程度的数量表示,其公式如下: (19) 7个影响因素的关联程度如图4所示,流量的关联度评价最高(关联度:0.702),其次是流体密度(关联度:0.697),再次之是转子偏心距(关联度:0.662)。说明在水力振荡器工作过程中,流量、流体密度以及转子偏心距对其轴向力影响最大。 图4 各影响因素关联度 克拉玛依油田艾湖2井区某油井,完钻井深5 505 m,垂深3 422.74 m,水平段长1 934 m,井斜角88.4°,其井身结构如图5所示。 图5 井身结构 该井钻磨桥塞过程中所使用的螺杆式连续油管水力振荡器尺寸规格为7.3 cm(2.875 in)。水力振荡器各项参数:动阀板偏心孔半径r1为8.43 mm,动阀板偏心孔偏心距e为4.22 mm,静阀板孔半径r2为7.87 mm,转子偏心距E为6.02 mm,转子半径R为14.50 mm,转子螺距h为309.39 mm,动阀板壁厚δ为7.87 mm,动阀板弹性模量210 GPa。连续油管参数:外径D为50.8 mm,内径d为42 mm,连续油管密度ρ为7 850 kg/m3。其他参数:钻磨液密度ρ为1 030 kg/m3,流量Q为350 L/min,重力加速度g为9.8 m/s2。 根据灰色关联度分析结果,流量、流体密度以及转子偏心距对水力振荡器轴向力影响最大。对不同流量、流体密度以及转子偏心距下,水力振荡器轴向力变化情况进行研究。当水力振荡器在流量分别为350、375、400 L/min时,不同流量下轴向力随时间变化曲线如图6所示,水力振荡器最大轴向力分别为6 395.9、6 852.8、7 309.7 N。随着泵流量的增加,水力振荡器最大轴向力逐渐增大,轴向力变化频率逐渐增快。 图6 不同流量下轴向力 当水力振荡器在流体密度分别为1 000、1 200、1 400 kg/m3时,不同流体密度下轴向力随时间变化曲线如图7所示,水力振荡器最大轴向力分别为6 302.1、6 903.6、7 456.8 N。随着流体密度的增加,水力振荡器最大轴向力逐渐增大,但对轴向力变化频率无影响。 图7 不同流体密度下轴向力 当水力振荡器转子偏心距分别为5、6、7 mm时,不同转子偏心距下轴向力随时间变化曲线如图8所示,水力振荡器最大轴向力分别为5 894.6、6 386.4、6 848.0 N。随着转子偏心距的增加,水力振荡器最大轴向力逐渐增大,但轴向力变化频率逐渐减小。 图8 不同转子偏心距下轴向力 (1)根据螺杆式连续油管水力振荡器工作过程中的运动和受力分析,得出其轴向力计算公式。 (2)采用灰色关联度对影响水力振荡器轴向力的因素进行了影响程度分析,得出流量、流体密度以及转子偏心距对水力振荡器轴向力影响最大。 (3)根据灰色关联度分析所得结果,对不同流量、流体密度以及转子偏心距下,水力振荡器轴向力变化情况进行研究。结果表明:水力振荡器最大轴向力随流体密度、流量以及转子偏心距的增加而变大;水力振荡器轴向力变化频率与流体密度无关,随流量增加而变大,随转子偏心距增加而减小。
1.3 轴向力分析
2 轴向力影响因素分析

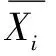


3 实例计算


4 总结

