乏燃料后处理用空气提升器仿真模型研究及验证

宋金阳，赵 强,*，周 羽，陈 勇

（1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150009；2.中国核电工程有限公司，北京 100840）

在乏燃料后处理过程中，由于所涉及的料液放射性水平高、辐照剂量大，在检修过程中要避免工作人员遭到辐射，普通的机械结构泵无法满足要求。空气提升器设备简单、无传动部件、无维修部件、可靠性好，且维护成本更低[1]，这样的特点很好地满足了输送具有放射性和腐蚀性料液的需求，于是空气提升器被广泛应用于乏燃料后处理工艺，特别是在后处理厂和高放废液玻璃固化车间得到了大量应用[2]。空气提升器作为乏燃料后处理过程中重要的流体输送设备，对其性能的仿真研究是乏燃料后处理系统仿真中的重要环节。

早在19 世纪空气提升器就已经被应用于油井开采，但直到20 世纪，研究者们才开始陆续对空气提升器进行理论分析。1963 年，Nicklin[3]首次根据动量平衡对空气提升器进行了分析，研究了不同流型对空气提升器效率的影响，同时提出了空气提升器效率的计算方法；1968 年Stenning[4]以动量平衡为基础，考虑了气液两相之间的相对漂移速度建立了空气提升器分析模型。在计算两相流摩擦压降时，Stenning 将单相摩擦损失的计算方法扩展到两相流进行计算，导致该模型误差较大；1980 年Parker 等人[5]通过实验分析，在Stenning 的模型基础上增加了对气体注入方式的修正。张成刚等人[6]通过实验验证了Parker 模型对多种流体的有效性；景山等人[7]对空气提升器在后处理脉冲萃取柱上的应用进行了研究；胡东[8]、Wang 等人[9]以两相流分析为基础，对空气提升器进行了较为完整的动量守恒分析；但现有的模型研究并没有深入考虑管径对垂直上升两相流的影响，这将影响模型对于不同管径空气提升器的仿真精度。

本文基于动量守恒基本原理，分析垂直上升两相流特性，选取适用于不同管径的两相流特性计算方法，建立了空气提升器仿真模型，编写了Fortran 计算程序并得到计算结果。最后使用实验台架完成了空气提升器验证实验，通过计算结果与实验数据的比较分析，验证了计算模型，得到10～40 mm 管径空气提升器仿真模型。

1 空气提升器建模

1.1 空气提升器动量分析

空气提升器的结构模型如图1 所示，E为升液管的吸入口，O为升液管的排出口，I为空气注入口。EI 单相段长度为L1。液体与空气在I 处混合后的两相段长度为L。水平面至空气注入口的距离为浸没高度H。

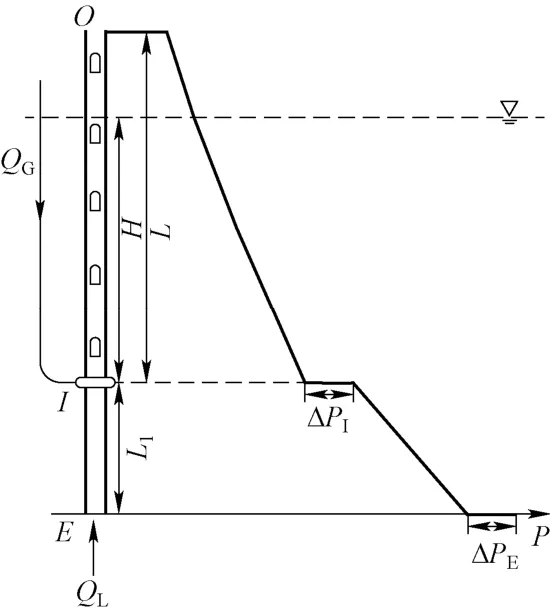
图1 空气提升器结构及压强分布示意图Fig.1 The schematic of the airlift pump structure and pressure distribution

首先对空气提升器进行动量分析，在空气提升器内，流体单位时间所受到的合力等于流出与流入的动量差。

式中：F——吸入口E 所受水的静压；

G——升液管内单流体所受重力之和；

fEI——EI 段单相流流体所受阻力；

fIO——IO 段两相流流体所受阻力。

式中：A——空气提升器横截面积，m2；

ρ——液体密度，kg·m-3。

式中：εG——截面含气率，εL=1-εG。

fEI由单相流的摩擦损失和E 处的入口局部压力损失组成。

式中：λL——达西摩擦因数；JL——液相表面速度。

E 处为突缩入口，其局部压力损失为：

式中：ξE——局部阻力系数，对突缩局部压损通常取值为0.5。

fIO由两相流的摩擦压力损失和I 处空气注入引起的液体加速压降组成。

空气提升器流出和流入的动量I1、I2分别为：

将以上方程带入动量方程（1），可得到空气提升器的总动量平衡方程：

两相流截面含气率εG与两相流梯度压力损失 Δpf,GL/Δz是气液两相流中重要的特性参数，是两相研究中的重点。这两个参数的计算将会对空气提升器仿真模型的计算精确度产生很大影响，下文将对这两个参数的计算进行详细讨论。

1.2 压力变化对空气提升器两相流的影响

两相流在空气提升器的提升过程中所受压力逐渐减小，将导致两相流中气体的体积发生膨胀，进而使两相流截面含气率以及两相流的摩擦压降发生变化。为了正确体现空气密度变化对于两相流的影响，需要对升液管IO 段表面速度JG进行积分计算。

两相流在I 处所受压力为PI，在升液管出口，两相流的压力为大气压Pat。假设从I 点到O 点升液管内的压力是随轴向高度z线性变化的。

式中：T——绝对温度。

假设温度恒定，空气密度即为压力的函数，则升液管轴向高度决定了升液管内两相流中气相的密度。

表面速度JG与空气密度之间的关系为：

在输入空气质量流量MG固定的情况下，空气的表面速度JG为气相密度的函数，也就是升液管轴向高度z的函数。

1.3 升液管内两相流特性计算

空气提升器的工作区间绝大部分处于弹状流流型，在弹状流下空气提升器会有较高的运行效率。管径是影响弹状流形态的重要参数，管径的增大将导致弹状气泡的不稳定性增加，从而与较小管径下的垂直管上升弹状流产生明显区别。所以在建模时分别采用适用于大管径与小管径的两相流特性计算方法，建立大管径模型与小管径模型，以保证在不同管径下两相流特性的计算精度。

1.3.1 小管径空气提升器模型

对于小管径空气提升器，选用了以下适用于小管径垂直上升弹状流的计算公式。

Ishii[10]以 Zuber-Findlay 漂移流模型为基础，提出了适用于垂直上升弹状流的截面含气率计算公式。

对于摩擦压降的计算，采用Mishima[12]修正的Chisholm 两相流压降计算公式，该计算公式基于Chisholm 对Lockhart-Martinelli 实验结果的拟合，适用于低压力条件下两相流摩擦压降的计算。

1.3.2 大管径空气提升器模型

在大管径截面含气率的计算上依然以Zuber-Findlay 漂移流模型为基础。Hatakeyama[13]推荐采用Ishii 所提出的分布参数计算公式（20）与Kataoka 所提出的漂移速度计算公式组成的漂移流模型对大管径下的截面含气率进行计算。

Kataoka 基于在各种实验条件下获取的大量实验数据，将漂移速度构建为黏度、管径和密度比的函数：

当Nμf≤2 .25 ×10-3时：

在大管径两相流摩擦压降的计算上，Hatakeyama[14]以Chisholm 两相流压降计算公式为基础，通过对实验数据进行拟合，找到分布参数C与管径之间的对应关系。

2 验证实验设计

为了验证空气提升器仿真模型的计算结果，需要设计空气提升器实验台架，对空气提升器的提升性能进行实验，研究不同管径、不同浸没度下空气提升器的性能。台架的总体设计示意图如图2 所示。

实验装置采用空压机作为气源，将空气加压储存在储气罐内，进气经冷干机和精密过滤器预处理后通过稳压阀，由稳压阀初步调节进气压力。稳压阀后设置了0～50 L/min 和30～300 L/min 两个质量流量控制计，用于调整进气流量。压缩空气通过气体分布器进入升液管，将升液管中的液体提升至溢流槽。在溢流槽内，两相流的气相和液相互相分离，液体可通过重力自流或泵回流至储水槽，回流管路中设置了0～100 L/h、80～800 L/h 和600～6 000 L/h 流量计，其中0～100 L/h 流量计为浮子流量计，80～800 L/h 和600～6 000 L/h 流量计为电磁流量计，准确度等级为0.5 级，用于测量不同流量下的液体。储水槽分直筒段和下部水槽，配置差压变送器，用于测量储水槽内的液位高度。升液管、气体分布器和溢流水槽为有机玻璃材质，便于观察上升气液混合物状态。配置不同尺寸升液管和气液分布器，用于研究不同实验条件下提升性能。

实验分别对管径为10 mm、20 mm、30 mm和40 mm 的四种升液管在三种浸没度(Sr)下进行了测试，升液管高度L均为3.02 m，单相段长度L1为0.27 m。由于空气提升器在工作时流量呈现脉动特点，在实验过程中设置计算机每5 s 记录一次流量计数据，在数据处理时，将固定气量下 2 min 以上时长的数据点取均值作为该气量所对应的流量值。

3 结果和讨论

3.1 实验现象分析

如图3 所示，在20 mm 管径下，弹状流的弹状气泡无论是长气泡还是短气泡，其形态都较为稳定，弹状气泡与管壁之间的液膜较薄且流动稳定，液膜的回流只在弹状气泡的尾部产生了一些小气泡，两个弹状气泡可以稳定地夹带中间的液体上升。当管径增大至40 mm 管径时，由于管径较大，弹状气泡不能稳定地占据管道截面，弹状气泡头部发生了明显的变形。

图3 20 mm 与40 mm 管径弹状流形态Fig.3 The slug flow in 20 mm and 40 mm diameter tube

图3（c）可以观察到弹状气泡右侧的液膜要厚于左侧的液膜，液体通过右侧液膜产生了较大的回流，导致弹状流夹带效果减弱。同时，回流的液体堆积在弹状气泡尾部的右侧，并冲击弹状气泡后的液体，产生了更多的小气泡，增加了两相流的摩擦压降。这样的现象说明，当管径达到40 mm 时，其内部的弹状流已与小管径弹状流出现明显的区别，需要采用不同的两相流特性计算方法。

3.2 结构参数对模型计算结果的影响

在空气提升器模型的建模过程中充分分析了空气提升器的物理结构，考虑了空气提升器管径、浸没度、升液管长度等参数对空气提升器性能的影响。

总体上看，通过模型所计算出的空气提升器性能曲线在不同参数下均有以下相同特点：在空气流量较小时，液体流量与空气流量基本呈线性关系快速上升，随着空气流量增加，液体流量增速开始减慢，当液体流量达到最高点后，继续增加空气流量将导致液体流量缓慢下降。这与空气提升器的实际工作情况一致。

图4 中，不同管径之间提升性能差异巨大，管径每增加一倍，空气提升器对空气流量的需求及空气提升器提升的液体的能力都将成倍增加。

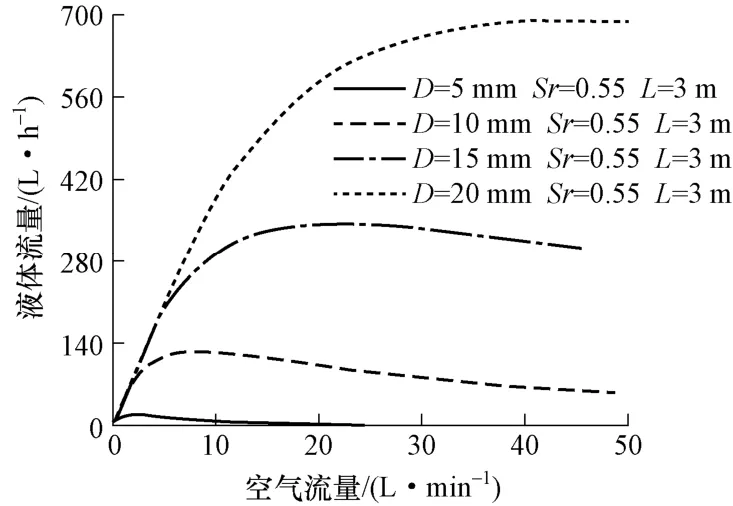
图4 模型对不同管径的计算结果Fig.4 Calculation results of the model for different pipe diameters

图5 中，当浸没度增加时，空气提升器的底部静压增加，其提升性能也会随之增加。同时，由于升液管长度L相同，浸没度的增加会导致液面与升液管出口之间的提升高度减小。体现在计算结果上为性能曲线向上偏移，即在相同的空气流量下，高浸没度相比于低浸没度可以提升更多的液体。

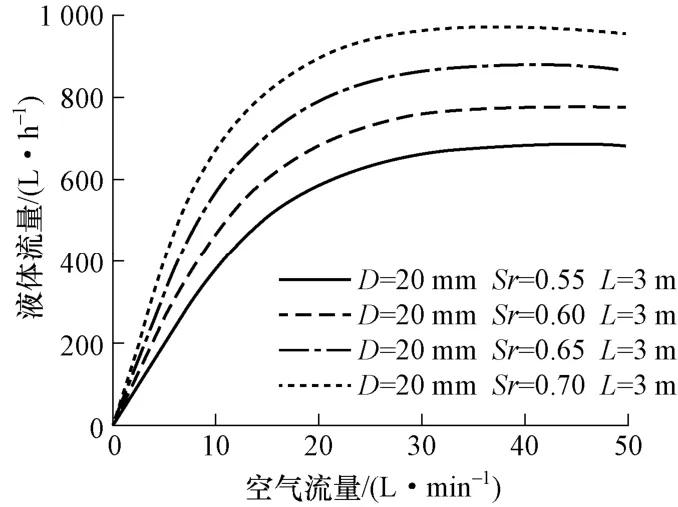
图5 模型对不同浸没度的计算结果Fig.5 Calculation results of the model for different submergence ratios

图6 中，在空气流量较小时，四条曲线基本重合。随着空气流量增加，由于升液管长度较长的空气提升器其底部有更强的静压，所以在相同空气流量下其提升的能力将会高于升液管长度较短的空气提升器。不过利用升液管长度提高空气提升器的性能的幅度是有限的，因为在浸没长度增加的同时，液面上方的提升高度也在增加，静压所带来的性能提升将会与提升高度带来的性能损失逐渐互相抵消。

图6 模型对不同管长的计算结果Fig.6 Calculation results of the model for different pipe length

以上由于结构参数变化导致的空气提升器性能曲线变化的趋势均符合空气提升器的实际工作情况，所以，本文所提出的空气提升器模型可以正确体现结构参数对于空气提升器性能产生的影响。

3.3 模型验证

首先将实验数据与小管径空气提升器模型的计算结果进行对比。

如表1 所示，小管径空气提升器模型对于10～30 mm 管径的空气提升器得到了较好的预测结果，说明小管径模型采用的两相流特性计算公式适用于10～30 mm 管径的空气提升器，但在40 mm 管径的预测上误差明显增大，需要采用不同的计算方法。

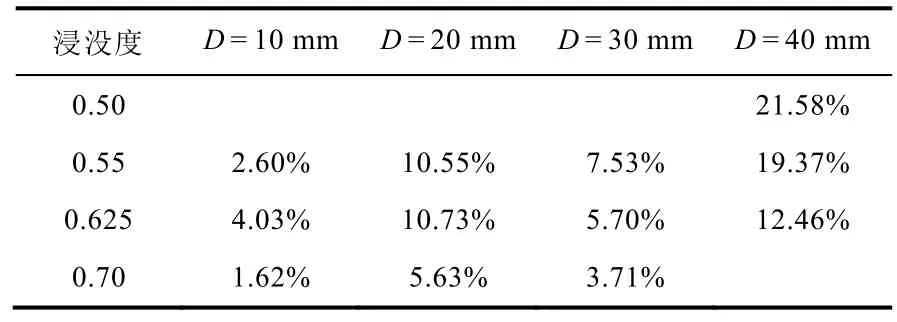
表1 小管径模型的相对误差Table 1 The relative error of small pipe diameter model

如表2 所示，通过将实验数据与大管径模型进行对比发现，大管径模型对于40 mm 管径空气提升器性能的预测相比于小管径模型有了显著的提升，在对30 mm 管径的相对误差则要大于小管径模型，所以大管径模型更适合对管径大于40 mm 的空气提升器性能进行预测，这也与实验观察到的现象相符。

表2 大管径模型的相对误差Table 2 The relative error of large pipe diameter model

通过对两组相对误差进行分析，建议在10～33 mm 时采用小管径模型，在33～40 mm 采用大管径模型，所得到的仿真模型可以对10～40 mm 管径空气提升器进行准确预测，总体结果如图7 所示。

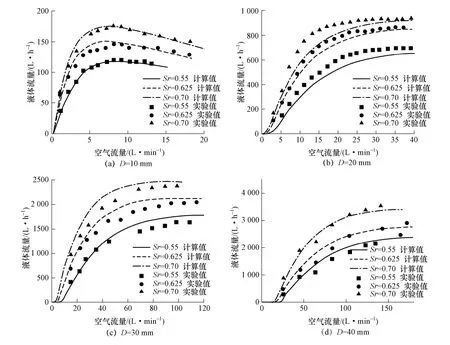
图7 模型在10-40 mm 管径下计算值与实验值对比Fig.7 Comparison of calculated and experimental data in 10-40 mm diameter tube

在建模过程中，对于空气在升液管中发生膨胀的考虑有效提高了模型计算结果与实验结果的吻合度。如表3 所示，以小管径模型为例，相比于不考虑空气膨胀的计算结果，模型在10 mm 到30 mm 三个管径下均有效提高了预测精度，特别是在20 mm 管径下减小了约4%的相对误差。

图8 为模型与经典的Kassab[15]模型对于20mm 管径空气提升器在0.625 浸没度下计算值与实验值的对比分析。Kassab[15]模型中虽然考虑了气液两相的相对漂移，但没有采用专门用于气液两相流的摩擦压降计算方法；在计算过程中空气密度采用了恒定值，没有考虑空气上升过程中的膨胀。相比于Kassab[15]模型，本文所提出的模型采用的两相流特性计算公式适用性更强，并考虑了压力变化对空气密度的影响，所以相比于Kassab[15]模型，本文提出的模型计算结果与实验值的拟合度更高。

3.4 误差分析

本文所提出模型的计算结果与实验结果仍存在一定误差，误差主要来源于以下几点：

（1）空气提升器内两相流的气相和液相在流动过程中存在激烈且不规律的相互扰动，这会导致实验数据测量的过程中产生误差。

（2）现有的两相流特性计算公式均为经验公式或半经验公式，这些公式本身存在一定误差，且这些公式在不同的参数范围其误差也不同。

（3）空气提升器的进气方式对空气提升器的性能有一定的影响，由于进气方式在理论分析中难以量化，所以在本文中并未考虑这种影响。

4 结论

通过分析空气提升器的物理结构，根据动量守恒原理，构建空气提升器动量方程，使用适合于不同管径的两相流压降及截面含气率计算方法建立不同的计算模型，通过实验对计算结果进行验证，研究结果表明：

（1）使用Mishima 所提出的两相流压降公式与Ishii 所提出的截面含气率公式的小管径空气提升器仿真模型，适用于10～30 mm 管径，在0.55、0.625 和0.70 三个浸没下相对误差不大于11%

（2）当管径达到40 mm 时，空气提升器内的垂直上升弹状流出现了与10～30 mm 管径下不同的流动特点。

（3）使用Hatakeyama 所提出的两相流压降公式，Ishii 漂移流分布参数计算公式和Kataoka漂移速度计算公式的大管径空气提升器仿真模型适用于40 mm 管径，在0.50、0.55 和0.625三个浸没下的相对误差在8%左右。

（4）空气在空气提升器内的膨胀将会对空气提升器的性能产生一定影响，在建模过程中通过考虑空气膨胀带来的影响可以显著减小模型的误差。

本文所提出的模型具有较广的应用范围，可被应用于乏燃料后处理各个过程中用于输送放射性料液的10～40 mm 管径空气提升器，也可以对其他行业所采用的10～40 mm 管径空气提升器进行模拟仿真。