基于提升初中生元认知能力的复习课教学实践

［摘  要］ 元认知能力是学生对自我认知过程的有效监控，表现为围绕学习目标进行自主的学习和研究，并能主动地对所学知识提出疑问，进行猜想验证和自我调节，从而提升自主学习能力. 在复习课教学中，教师要明确复习目标，引导学生在复习过程中对探究过程进行监控和把握，并在不断尝试和筛选中自我调节，在不断总结中升华认识，从而提升元认知能力.

［关键词］ 元认知；复习课教学；自我调节；思维能力

初中数学复习课对于强化学生对知识的理解、提升思维能力等具有非常重要的意义. 在复习课教学中，教师要引导学生进行自主学习、自我监控、调节探究知识的过程，学会在不断的尝试中归纳、总结知识，从而提升元认知能力.

何谓元认知能力

马扎诺的教育目标分类学中提出元认知系统，元认知，也可以称为反省认知，是指对自我认知的监控和调节，能够从根本上调节认知过程，深化知识理解. 元认知是主体对自我的一种认知，重视元认知能力的培养能够提升学生对思维学习活动的监控，从而提高学习效率.

教师要鼓励学生参与和控制学习过程，学会主动探究和总结知识，并在自我探究中主动发现问题，进行质疑问难，从而在自我尝试中消除各种误解，并对接下来的学习活动进行判断和自我调控.

教学实录

笔者在教学实践中尝试对学生进行元认知能力的培养，在八年级期末复习时，笔者布置了一道课后作业，请学生设计一道以一次函数和反比例函数相结合为背景的，能够根据已知条件通过设点的坐标进行求解的问题.

1. 环节1：温故知新，明确本课探究目标

师：上节课我们有这样一道例题.

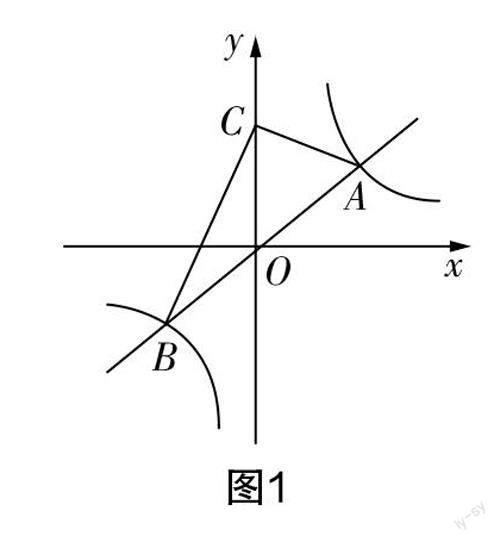
如图1所示，一次函数y=（3/4）x与反比例函数y=k/x（k>0）的图象相交于第一象限的A点及第三象限的B点，点C在y轴的正半轴上，∠ACB=90°，并且△ACB的面积为10，求反比例函数中k的值.

师：大家还记得我们是如何解决这道题的吗？

生1：本题出现了A，B，C三个点，所以我们可以利用点的坐标来解决问题.

生2：题干已知一个直角三角形的面积，因此我们可以从已知三角形的面积去求三角形各边的边.

师：本题出现了三个点，那么在解题过程中我们到底应该选择哪个点的坐标来入手呢？

生3：一般选择已知直线上的点来设坐标以解决问题.

生4：我们还可以把OC看作底边，利用直角坐标系化斜为直进行转化求解.

师：同学们的思路都非常好，我们可以利用这道题进一步拓宽我们的视野. 大家可以参照这道题的思考方向寻找相关的问题.

2. 环节2：强化目标，分析自选试题

学生自选题1：如图2所示，一次函数y=x（x≥0）的图象上有一点A，直线l过点A并且与x轴垂直，点B在直线l上且在点A上方，以AB为斜边在AB右侧作等腰直角三角形ABC，且反比例函数y=（x>0）的图象经过B，C两点. 连接OB，若△OAB的面积为6，求△ABC的面积.

师：同学们观察一下，这道题与我们研究的主题有关系吗？

生（齐）：这道题是以一次函数和反比例函数相结合为背景的，并且能够从点的坐标切入，和我们研究的主题是相关的.

师：哪位同学能具体讲一讲如何解决这道题吗？

师：大家还有不同的解法吗？

生9：我本来不知道应该怎么求点C的坐标，但是听了生8的CM=DO后，受到启发，觉得可以利用平行线将△ABC的面积转化为△ABD的面积，这样就能直接求出点D的坐标为（0，8）了.

3. 环节3：提升思维，分享选题过程

师：刚才大家的讨论非常热烈，也给我们提供了很多新的想法. 现在我们来听一听提供这两道题的同学的想法，让他们说说选这两道题的原因.

选自选题1的学生：首先这道题的解题思路与我们原有的探究目标一致，如已知线段与点坐标的转化、一次函数与反比例函数的结合、直角三角形面积与边的长的转化等. 因此，根据这个思维方向，我们可以通过设点A的坐标，根据已知条件表示出点B和点C的坐标，由此突破问题难点.

选自选题2的学生：我选这道题是因为有的同学说不太理解“两条平行线之间的等面积问题”. 我认为这个知识点是一个难点，所以我在想能不能从考查这个知识点的角度出发来出题. 自选题2就运用了两条平行线间等面积的知识，因此我选择这道题来和大家共同探讨.

师：对于自选题2，大家没有正面求解点C的坐标，而是将其进行了转化，但是我们本课研究的重点是通过设点的坐标突破试题难点，所以你们有没有什么方法可以直接求出点C的坐标呢？

生10：本题的已知直线是y=-（1/2）x，在这条直线上有一点M，我们可以设点M的坐标为（-2m，m）. 由于CM的长度为8，所以点C的坐标可以表示为（-2m，m+8）. 又点C在双曲线y=（-18/x）上，所以可以得到方程-2m·（m+8）=-18.

4. 环节4：交流感想，提升元认知能力

师：在这节课中，你们展示了自己選择的试题，大家也采用多种方法进行了解题的尝试. 在解题过程中，你们提出了自己的困惑，且通过交流进一步完善了自己的解题思路. 现在，请大家回顾一下本课的研究过程，谈一谈自己的感受.

生11：准备自选题1的同学在寻找例题的时候具有明确的目标，使我们能够结合已学的知识，进行相关问题的论证. 通过这道题的练习，我们可以更加熟练地进行已知线段与坐标之间的相互转化.

生12：准备自选题2的同学关注到了我们学习中的困难. 解决自选题2能让我们将学习中的困惑转变为学习的经验，并在具体的解题实践中消除大家学习中的知识盲点.

教学反思

1. 在本课例中，学生从已学知识出发，有目标地选择相关问题进行研究. 这正是元认知系统中，要教会学生如何进行学习，怎样对学习进行有效的自我调节的具体体现. 在教学中，学生根据研究目标主动确定例题，这是落实学生主体地位的体现，能让学生在学习过程中增强主人翁意识，提高探究学习的积极性，这体现了学生对研究过程的有效监督和把控.

2. 元认知系统要求学习者对认知过程进行有效监控，即在解决相关问题的过程中能够主动进行学习和探究. 在本次教学实录中，学生能主动对例题进行研讨，且从多种角度进行思考，增强了创新意识，培养了发散思维. 学生能够在学习过程中主动对研究的问题进行探讨和调节，这能增加他们理解知识的深度和广度.

3. 学生在研究的过程中必然会遇到各种障碍和困难，当学生在思维上出现瓶颈时，教师可通过引导学生展示自己在思考过程中的困难进行解题探讨，帮助学生突破认知难点，这也体现了元认知系统中的监控和调节功能. 教师在教学过程中应尽量引导学生发现思维的困惑点，找到出现思维困惑的原因，从而找到解决困惑的办法.

总之，元认知系统的核心在于强调学生主体在认知活动中能够确定目标，并对认知的过程进行监控和调节，从而提升思维能力. 教师在课堂教学中要引导学生围绕学习目标进行自我实践和尝试，并在实践过程中通过交流不断更新自己的观点，提升元认知能力，从而真正学会学习.

作者简介：任春晓（1970—），本科学历，中学一级教师，从事初中数学教学与研究工作.